Academia de Studii Economice
BAZELE CIBERNETICII
Facultatea de Cibernetica,
Statistica si Informatica Economica
Se da un model cibernetic in forma continua in care se urmaresc variabilele venit y si rata dobanzii r.
Relatiile de dinamica sunt:
I) ![]()
II) ![]()
unde
D este cererea de produse si D(t) = a11 y(t) + a12 r(t) + G ;
MD este cererea de bani si MD(t) = a21 y(t) + a22 r(t) ;
MS este oferta de bani, presupusa a fi fixata ;
G reprezinta cheltuielile guvernamentale.
Se cere:
a) Sa se scrie relatiile de dinamica in forma matriceala avind ca variabile de stare (endogene) pe y si r iar ca variabile de comanda (exogene) pe G (cheltuielile guvernamentale) si MS (oferta de bani);
b) Pentru valorile date
a = 0 b = 0,5
a11 = 0 a12 = -3
a21 = 0,25 a22 = -1
sa se studieze stabilitatea sistemului;
c) Daca G = 400, MS = 450 sa se afle o traiectorie de echilibru pentru sistemul diferentiar.
Are aceasta traiectorie o comportare oscilanta periodica (ciclica)?
a) Notam ![]() si
si ![]() .
.
Inlocuind in relatiile de dinamica functiile cererea de produse si cererea de bani, acestea devin:
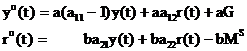
Deci, sub forma matriceala sistemul se poate scrie astfel:
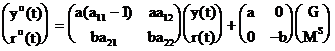
Notam: 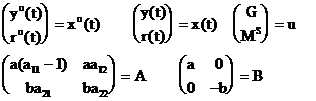
Cu noile notatii sistemul se poate scrie: ![]() .
.
Sistemul este stationar deoarece matriciile A si B nu depind de timp.
b) Consideratii teoretice. Studiul stabilitatii unui sistem liniar continuu.
Definitie: Stabilitatea este acel caracter general al sistemului prin care se reflecta mentinerea unei proportii relativ stabile intre componentele sistemului.
Dupa capacitatea de sinteza a sistemului studiat avem doua feluri de stabilitate:
stabilitate globala atunci cand covergenta sistemului spre traiectoria de echilibru nu depinde de alegerea solutiei initiale;
stabilitate locala atunci cand covergenta sistemului spre traiectoria de echilibru depinde de alegerea solutiei initiale.
Analiza stabilitatii:
Fie sistemul ![]()
Partea omogena ![]() are solutia
are solutia ![]() . Aceasta este componenta
proprie a traiectoriei de evolutie, notata
. Aceasta este componenta
proprie a traiectoriei de evolutie, notata ![]() .(pentru
.(pentru
![]() avem
avem ![]() , unde k este un vector coloana ce se determina pornind de la
conditiile initiale)
, unde k este un vector coloana ce se determina pornind de la
conditiile initiale)
Traiectoria starii va fi data de expresia:
![]() ,
,
unde xD(t) este componenta de dirijare, corespunzatoare formei particulare a deciziilor luate.
Sistemul nostru este:
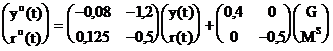
Calculam componenta proprie, care este solutie a
ecuatiei omogene ![]()
![]()
Pentru a putea calcula ![]() este necesara
descompunerea in forma Jordan a matricei A.
este necesara
descompunerea in forma Jordan a matricei A.
Rezolvam ecuatia: ![]()
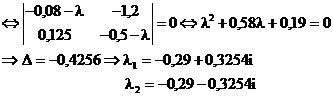
Notam ![]() , unde
, unde ![]()
Matricea Jordan va fi de forma ![]()
Valoriile
proprii sunt complex conjugate, deci si vectorii proprii vor fi complecsi
conjugati.
Pentru determinarea vectoriilor proprii rezolvam ecuatia ![]()
![]() , in forma lui Moivre
, in forma lui Moivre ![]() .
.
s=3.0982
Matricea vectoriilor proprii este:
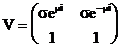 , iar
, iar 
In descompunerea Jordan, matricea A se scrie: ![]()
Acum ecuatia traiectoriei starii se poate scrie:
![]()
sau
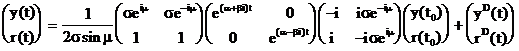 .
.
Efectuand inmultiriile si folosind formulele lui Euler, ecuatia traiectoriei starii devine:
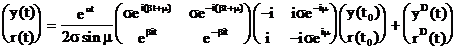
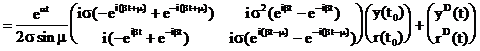
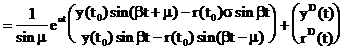
unde ![]() sint constante
(numere).
sint constante
(numere).
Ecuatiile traiectoriilor starii venitului si a ratei dobinzii sint:
![]() ,
,
![]()
Notam cu ![]()
![]()
Ecuatii se pot scrie astfel:
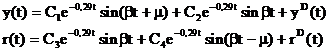
Trecem la limita cele doua ecuatii:
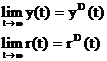
deci cele doua traiectorii tind in timp spre traiectoriile de echilibru caracterizate de componenta de dirijare ceea ce inseamna ca sistemul este stabil in timp. Stabilitatea sistemului este globala (convergenta sistemului catre traiectoria de echilibru nu depinde de valorile initiale y(t0) si r(t0)).
c) Consideratii teoretice. Determinarea traiectoriei de echilibru.
Vom porni de la ecuatia matriceala de dinamica a
starii de forma: ![]()
Componenta proprie a traiectoriei de evolutie a
starii sistemelor descrise de ecuatia de mai sus este: ![]() , unde k este vector coloana
ce se determina pornind de la conditiile initiale.
, unde k este vector coloana
ce se determina pornind de la conditiile initiale.
Deoarece fluxurile de intrare sunt considerate
constante, avem ![]()
In consecinta, se va cauta o solutie particulara de
aceeasi forma ![]() , unde d este un vector
coloana bidimensional real, deci un vector de constante. Solutia particulara
, unde d este un vector
coloana bidimensional real, deci un vector de constante. Solutia particulara ![]() va verifica ecuatia de dinamica a starii, adica:
va verifica ecuatia de dinamica a starii, adica: ![]()
Dar cum ![]() 0, avem
0, avem ![]() , expresie care prin
inmultire la stinga cu
, expresie care prin
inmultire la stinga cu ![]() devine
devine ![]() . In concluzie, componenta de dirijare are
forma
. In concluzie, componenta de dirijare are
forma
![]()
iar traiectoria starii va fi data de expresia
![]()
Am aratat in punctul trecut ca traiectoria starii
converge in timp catre componenta de dirijare ![]() . Vom
determina aceasta componenta.
. Vom
determina aceasta componenta.
In cazul nostru ![]()
Deci ![]()
Rezultatul este
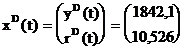
Dupa cum se observa ambele traiectorii de echilibru ale venitului si ratei dobinzii sunt constante in timp, deci nu are o comportare oscilanta periodica.
|
Politica de confidentialitate |
| Copyright ©
2024 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |