Determinarea pozitiei centrului de masa pentru un corp omogen de o forma oarecare
Determinarea pozitiei centrului de masa pentru un corp omogen de o forma oarecare , necesita parcurgerea urmatoarelor etape :
Se descompune corpul intr-un numar minim de corpuri componente simple ale caror centre de masa sunt cunoscute sau se pot calcula cu relatiile din tab. 1.
Pentru fiecare corp component se alege cate un sistem de referinta propriu in asa fel incat sa se aduca simplificari in calcule . De exemplu daca un corp admite o axa de simetrie , acea axa va fi aleasa in cadrul sistemului de referinta
Se aplica corpurilor componente relatiile din tab. 3 tinand cont de urmatoarele observatii :
a ) - coordonatele centrelor de masa ale corpurilor componente calculate fata de sisteme de referinta proprii alese conform etapei a II-a , se vor raporta fata de sistemul de referinta impus in problema ( este de cele mai multe ori indicat in figura ) pentru corpul omogen de forma oarecare ;
b ) - elementele caracteristice ( mi , li , Ai , Vi ) ale corpurilor componente care se scot din corpul omogen se considera negative .
c ) - tabelul trebuie sa contina un numar minim de linii si coloane . Numarul minim de linii se obtine impartind in modul cel mai judicios corpul dat . Numarul minim de coloane se obtine prin alegerea convenabila a sistemului de referinta conform observatiei 2 .
Tab. 3 . Calculul pozitiei centrului de masa pentru un corp omogen de forma oarecare
|
Nr. corp |
Desen corp component |
xi |
yi |
zi |
mI, li Ai Vi |
mi xi li xi Ai xi Vi xi |
mi yi li yi Ai yi Vi yi |
mi zi li zi Ai zi Vi zI |
|
i | ||||||||
|
n | ||||||||
|
Σ | ||||||||
d ) - se efectueaza suma pe verticala a ultimelor rubrici din tab. 3 , prima suma (1) reprezentand numitorul relatiilor din tabelul 1 , iar celelate sume (2), (3) si (4) reprezentand numaratorul acelorasi relatii
e) - Astfel, coordonatele centrului de masa sunt date de relatiile :
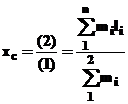pentru corpuri
punctiforme avand drept element caracteristic masa 
pentru corpuri de tip
bara avand drept element caracteristic lungimea 
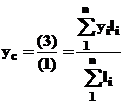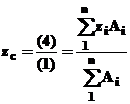pentru corpuri de tip bara
avand drept element caracteristic aria 
Teoremele GULDIN - PAPPUS
Teorema 1
Aria suprafetei rezultate prin rotirea completa a unui arc AB omogen si cuprins in planul axei de rotatie ( D ) pe care nu o intersecteaza este egala cu produsul dintre lungimea arcului AB si lungimea cercului descris de centrul sau de masa
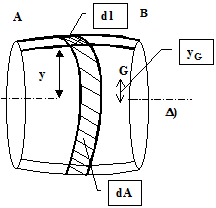
Demonstratie
Se considera arcul AB prezentat in figura
7 , care se roteste in jurul axei (Δ) fara
sa o intersecteze.
Prin rotirea in jurul axei ( D ), elementul de
arc dl va descrie un cilindru elementar a carei
arie laterala va fi :
Fig.7
dA = 2 py dl ( 28 )
Intoducand ( 30 ) in ( 29 ) se obtine :
A = 2 p yC LAB
Teorema 2
Volumul generat de o suprafata plana , omogena prin rotatia completa in jurul unei axe din planul sau pe care nu o intersecteaza este egal cu produsul dintre aria suprafetei plane considerate si lungimea cercului descris de centrul sau de masa in timpul rotatiei .
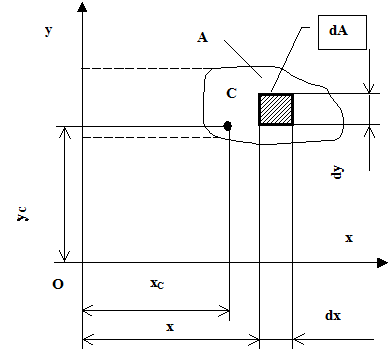
Fig.8
Demonstratie
Prin rotirea suprafetei A in jurul axei Oz ( figura 8), un element de arie dA va descrie un volum elementar dV:
(32)
Volumul generat de toata suprafata A va fi :
(33)
Observatie
Ambele teoreme raman valabile si in cazul in care rotatia nu este completa . Daca rotirea se produce cu un unghi β<2π atunci se inlocuieste in relatiile ( 31 ) si ( 33 ) 2p cu unghiul de rotatie b exprimat in radiani .
Aplicatia 1
Sa se determine pozitia centrului de masa pentru figura plana care constituie sectiunea transversala a unei contragreutati si este prezentata in figura 9.
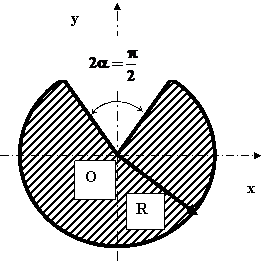
Fig.9
Rezolvare
In tabelul 4 este prezentat centralizat modul de rezolvare al aplicatiei 1.
Tab. 4 Rezolvarea aplicatiei 1
|
Nr. corp |
Desen corp |
yi |
Ai |
Aiyi |
||
|
|
| |||||
|
|
|
|
|
|||
|
|
|
|
||||
De unde :
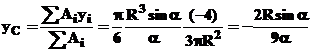
pentru:
Observatii
Datorita simetriei corpului xc = 0
Se observa ca impartirea in doua corpuri nu este optima ,deoarece corpul omogen poate fi considerat un caz particular de sector circular ( tab. 2 ) cu unghiul la varf:
si in acest caz este valabila relatia cunoscuta :
Aplicatia 2
Sa se determine pozitia centrului de masa pentru segmentul de coroana circulara plana din
fig . 10, folosit ca masa de dezechilibrare in cadrul unui vibrator mecanic .
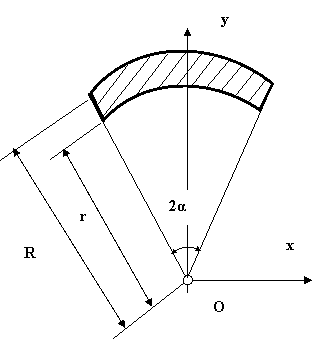
Fig.10
Rezolvare
In tabelul 5 este prezentat centralizat modul de rezolvare al aplicatiei 2.
Tabelul 5 Rezolvarea aplicatiei 2
|
Nr. corp |
Desen corp |
yi |
Ai |
Aiyi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
De unde rezulta :
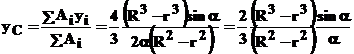
Aplicatia 3
Sa se determine pozitia centrului de masa si momentul static Sy pentru subansamblul unui vibrator (prezentat in figura 11) in doua situatii:
a ) luand in considerare numai masele de dezechilibru fara arbore ;
b ) luand in considerare intreg sistemul format din mase de dezechilibru si arbore
Se cunosc:
d = 0 , 03 m r = 7800 kg m3 R = 0 , 1 m
r = 0 , 06 m e = 0 , 02 m a = 0 , 05 m
b = 0 , 1 m l = 1 , 5 m a p
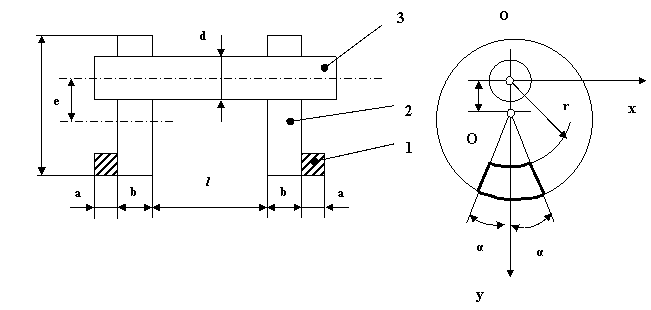
Fig.11
Rezolvare
In rezolvarea problemei se foloseste rezultatul de la problema precedenta referitor la pozitia centrului de greutate al segmentului de coroana circulara .
In tabelul 6 este prezentat centralizat modul de rezolvare al aplicatiei 3, pentru cazul a.
Tabelul 6. Rezolvarea aplicatiei 3
|
Nr corp |
Desen corp |
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
m1+m2 |
|
||
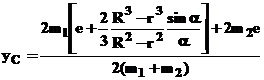
De unde rezulta :
m1 = p R2 a r = p 0,12 0,05 7800=12,5 kg
m2 = 2 a ( R2 - r2 )b r = 2p 3 ( 0,12 - 0,06 2 ) 0,1 7800 = 10,5 kg
Sy = 2 ( m1 +m2
) yC = ( 12,5 2 + 10,5 2 )
0,05 = 2,32 kg m
b ) Analog se obtine :
Aplicatia 4
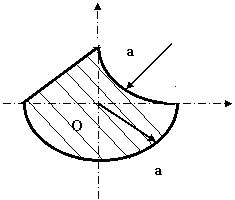Sa
se determine coordonatele centrului de masa pentru cama din fig. 12 , a
carei grosime este neglijabila .
Fig.12
Rezolvare
In tabelul 7 este prezentat centralizat modul de rezolvare al aplicatiei 4.
Tabelul 7. Rezolvarea aplicatiei 4
|
Nr. corp |
Desene corp |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|||||||||
|
C2 y2 x2 O |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|||||||||||
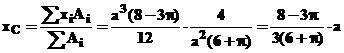
Utilizand relatiile din tab 7 se
obtin :
Aplicatia 5
Sa se determine coordonatele centrului de masa pentru nitul omogen din fig. 13.
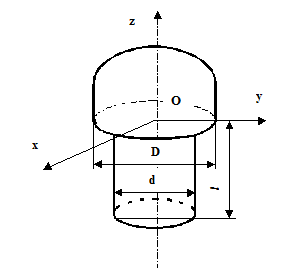
Fig.13
Rezolvare
Nitul compus din cilindrul l si semisfera 2 admite axa Oz ca axa de simetrie , ceea ce determina xC = yC = 0 . Coordonata zC se obtine folosind tabelul 8.
Tabelul 8. Rezolvarea aplicatiei 5
|
Nr corp |
Desen corp |
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||
De unde rezulta :
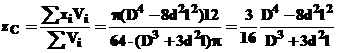
Aplicatia 6
Sa se calculeze volumul sferei de raza R aplicand a doua teorema Pappus - Guldin .
Rezolvare
Se considera semicercul de raza R care se roteste in jurul axei Ox si este prezentat in figura 14.
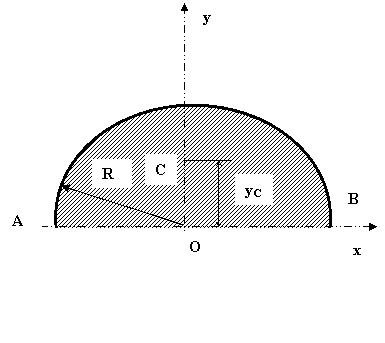
Fig.14
Volumul sferei este dat de relatia:
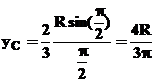
unde s-a tinut cont de:
|
Politica de confidentialitate |
 .com |
Copyright ©
2024 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |
