ECUATIILE DE ECHILIBRU LA INTERFATA
1. Introducere
Ecuatiile de echilibru (conservare) stabilite in capitolul 5 presupun continuitatea proprietatilor fizice asociate domeniului spatial D. Anumite aplicatii, de exemplu propagarea unei unde intr-un mediu continuu, necesita formularea ecuatiilor de echilibru pe o suprafata singulara ce se deplaseaza in mediul respectiv. Suprafata, aflata in miscare relativa fata de fluid, va determina astfel o discontinuitate a marimilor ce sunt continute in ecuatiile de echilibru; deci in formularea acestor ecuatii trebuie sa se tina seama de "saltul" (discontinutatea) marimilor respective.
Se considera o suprafata singulara ![]() ce se propaga cu viteza w intr-un mediu continuu D (v. figura 1). La un moment fix, suprafata
singulara (presupusa neteda, deci in fiecare punct al ei se
defineste o normala unica) imparte domeniul D in
doua domenii distincte, respectiv
ce se propaga cu viteza w intr-un mediu continuu D (v. figura 1). La un moment fix, suprafata
singulara (presupusa neteda, deci in fiecare punct al ei se
defineste o normala unica) imparte domeniul D in
doua domenii distincte, respectiv
![]() ,
, ![]() . (1)
. (1)
Campul ![]() , ce defineste o proprietate fizica in D
asociata mediului continuu (densitate, viteza, tensiune), va suferi
un salt intre cel doua fete ale suprafetei,
, ce defineste o proprietate fizica in D
asociata mediului continuu (densitate, viteza, tensiune), va suferi
un salt intre cel doua fete ale suprafetei,
![]() (2)
(2)
unde cu![]()
![]() s-a notat valoarea lui
s-a notat valoarea lui ![]() in
in ![]() .
.
2. Conditiile de salt pentru o suprafata singulara
In stabilirea ecuatiilor de echilibru se pleaca de la formularea
integrala a principiilor generale (v. capitolul 5), respectiv formulele de
transport (Reynolds) si formula lui Gauss. In cazul existentei
suprafetei singulare ![]() in domeniul D, ecuatia de
transport (5.11) pentru marimea
in domeniul D, ecuatia de
transport (5.11) pentru marimea ![]() capata expresia
capata expresia
![]() , (3)
, (3)
echivalenta cu
![]() , (4)
, (4)
unde s-a folosit formula lui Gauss (5.5) si (5.6) in forma
![]() (5)
(5)
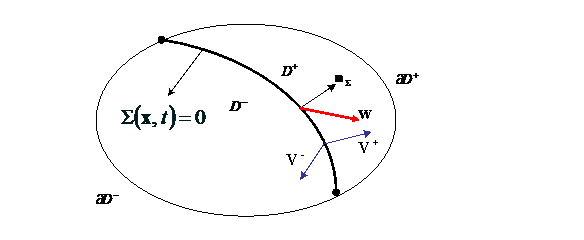
Fig. 1. Mediu continuu
parcurs de o suprafata singulara ![]() cu viteza w;
saltul vitezei mediului pe cele doua fete ale suprafetei este
cu viteza w;
saltul vitezei mediului pe cele doua fete ale suprafetei este ![]() .
.
In (3) si (5) ![]() reprezinta normala la suprafata singulara
reprezinta normala la suprafata singulara ![]() , sensul pozitiv fiind de la
, sensul pozitiv fiind de la ![]() catre
catre ![]() Relatiile
(3) si (5) se stabilesc plecand de la formele integrale initiale
scrise separat pentru domeniile
Relatiile
(3) si (5) se stabilesc plecand de la formele integrale initiale
scrise separat pentru domeniile ![]() si
si ![]() , domenii unde
, domenii unde ![]() este continua (pentru detalii a se
consulta bibliografia ).
este continua (pentru detalii a se
consulta bibliografia ).
Formele integrale ale principiilor generale se pot enuta generic prin relatia
![]() (6)
(6)
unde ![]() si
si ![]() reprezinta productia si aportul (din
exterior) de proprietate
reprezinta productia si aportul (din
exterior) de proprietate ![]() in D iar
in D iar ![]() este fluxul de
proprietate prin
este fluxul de
proprietate prin ![]() (v. tabelul 1).
(v. tabelul 1).
Tabelul 1
Marimile generice corespunzatoare principiilor generale
|
Principiu Marime |
|
|
|
|
|
Conservarii masei |
| |||
|
Conservarii impulsului |
|
|
T |
|
|
Conservarii energiei |
|
|
Tv - q |
Folosind (4) si (5) in (6) se obtine
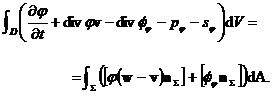
Considerand domeniul D un disc de volum infinitezimal in jurul
suprafetei ![]() (v. figura 2), in
limita
(v. figura 2), in
limita ![]() relatia de echilibru (7) este echivalenta cu
relatia de echilibru (7) este echivalenta cu
![]() (8)
(8)
unde ![]() reprezinta o eventuala
productie a proprietatii
reprezinta o eventuala
productie a proprietatii ![]() pe suprafata
pe suprafata ![]() (
(![]() se va considera nul daca nu se fac
precizari exprese).
se va considera nul daca nu se fac
precizari exprese).
Relatia (8) reprezinta conditia generala de salt" a marimii ![]() pe suprafata singulara
pe suprafata singulara ![]() . Pentru fiecare principiu general, in functie de
marimile
. Pentru fiecare principiu general, in functie de
marimile ![]() si
si ![]() corespunzatoare (v. tabelul 1), rezulta cate o conditie de
salt (v. tabelul 2).
corespunzatoare (v. tabelul 1), rezulta cate o conditie de
salt (v. tabelul 2).
Tabelul 2
Conditiile de salt asociate principiilor generale
|
Principiu |
|
|
Conditia de salt |
|
Conservarii masei |
|
|
|
|
Conservarii impulsului |
|
T |
|
|
Conservarii energiei |
|
Tv - q |
|
In (10) si (11)
![]() defineste
tensiunea pe interfata.
defineste
tensiunea pe interfata.
O suprafata
singulara pentru care ![]() si
si ![]() este o suprafata
materiala, deoarece saltul de viteza intr-un fluid incompresibil, in
cazul in care exista, nu poate fi decat tangential la
este o suprafata
materiala, deoarece saltul de viteza intr-un fluid incompresibil, in
cazul in care exista, nu poate fi decat tangential la![]() , straturile de fluid putand aluneca" cu
viteze diferite fata de
, straturile de fluid putand aluneca" cu
viteze diferite fata de ![]() (v. figura 3).
(v. figura 3).
Pentru o suprafata materiala conditia (9) este satifacuta prin definitie, respectiv M in (9), echivalent cu
![]() . (12)
. (12)

Fig. 3. Suprafata singulara ![]() este o
suprafata materiala; conditia (12) este
indeplinita chiar daca
vitezele fluidului in
este o
suprafata materiala; conditia (12) este
indeplinita chiar daca
vitezele fluidului in
lungul suprafetei sunt diferite in cele doua domenii.
Fie ecuatia
suprafetei materiale ![]() cu
cu
![]() ;
;
conditia (12), independenta de variatia densitatii, impune ca viteza normala a suprafetei sa fie egala cu viteza fluidului normala la suprafata respectiva, ceea ce este echivalent cu restrictia
![]() . (14)
. (14)
Deci, derivata
materiala (3.3) a unei suprafete materiale este prin definitie
zero, orice particula de fluid atasata la un moment dat de
suprafata ramanand in tot timpul miscarii pe
suprafata respectiva. ![]()
De asemenea, pe o suprafata materiala diferenta de tensiune pe interfata este nula
![]() , (15)
, (15)
iar puterea
mecanica a tensiunii pe interfata se transforma in
caldura (catre ![]() )
)
![]() . (16)
. (16)
Exemple de
suprafate materiale in campul curgerii sunt frontierele solide la care
fluidul adera, suprafetele de separatie dintre doua fluide
imiscibile prin care nu se realizeza un transfer de masa, respectiv
suprafetele de curent dintr-un fluid omogen, definite de conditia![]() (v. capitolul 2).
(v. capitolul 2).
3. Aplicatii
Una dintre cele
mai comune aplicatii ale conditiilor de salt (9) - (11) este calculul
vitezei undei de soc transmisa intr-un fluid ideal de miscarea
unui piston ce se deplaseaza cu viteza constanta u. In acest
exemplu, unda este reprezentata de o suprafata singulara ce
separa fluidul aflat in miscare cu viteza ![]() si fluidul aflat
in repaus
si fluidul aflat
in repaus ![]() , viteza undei fiind
, viteza undei fiind ![]() (v. figura 4).
(v. figura 4).
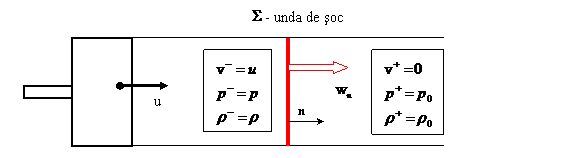
Fig. 4. Deplasarea unei unde de soc intr-un fluid ideal datorita miscarii unui piston.
Din conditia (9), echivalenta cu relatia
![]() (17)
(17)
se obtine
![]() . (18)
. (18)
Conditia de salt (10) proiectata pe directia normalei n devine
![]() , (19)
, (19)
respectiv
![]() (20)
(20)
Din (18) si
(20) se obtine legatura dintre cresterea de presiune datorata
undei de soc, ![]() , viteza undei si viteza de deplasare a pistonului,
, viteza undei si viteza de deplasare a pistonului,
![]() . (21)
. (21)
Daca se
cunoaste expresia energiei interne in mediul fluid, respectiv functia
de material ![]() , din (11) se poate obtine in principiu valoarea vitezei
undei de soc
, din (11) se poate obtine in principiu valoarea vitezei
undei de soc ![]() , unde c este viteza sunetului (celeritatea) si
, unde c este viteza sunetului (celeritatea) si ![]() sunt constante de
material (pentru
sunt constante de
material (pentru ![]() , deci
, deci ![]() , se poate arata ca
, se poate arata ca ![]() (pentru detalii se
poate consulta lucrarea mentionata la nota de subsol 1 din capitolul
1, v. si relatia (6.24)).
(pentru detalii se
poate consulta lucrarea mentionata la nota de subsol 1 din capitolul
1, v. si relatia (6.24)).
Aplicatiile
mai interesante apar cand se studiaza miscarea a doua fluide
aflate in contact. Daca restrictia (9) este admisa in
majoritatea cazurilor, in (8) ![]() , atunci conditia cinematica de aderenta
a fluidelor
, atunci conditia cinematica de aderenta
a fluidelor
![]() (22)
(22)
se poate considera valabila pentru toate miscarile studiate (acest lucru nu inseamna ca nu pot exista fizic cazuri ca cel prezentat in figura 3, respectiv fluide care nu adera la suprafetele care definesc domeniul curgerii).
Generalizarea
conditiei (10), respectiv a relatiei (15), trebuie insa
privita cu precautie. Daca suprafata singulara ![]() nu este materiala
nu este materiala
![]() sau
sau ![]() , diferenta tensiunilor din fluid ce
actioneaza pe interfata nu mai este nula. Acesta este
de exemplu cazul suprafetelor care separa doua faze (gaz-lichid)
sau doua lichide imiscibile in miscare. In ambele aplicatii
diferenta eforturilor normale ce actioneaza pe
, diferenta tensiunilor din fluid ce
actioneaza pe interfata nu mai este nula. Acesta este
de exemplu cazul suprafetelor care separa doua faze (gaz-lichid)
sau doua lichide imiscibile in miscare. In ambele aplicatii
diferenta eforturilor normale ce actioneaza pe ![]() este echilibrata
de eforturi generate de proprietati specifice ale fluidelor ce se
manifesta numai pe interfata: (i) tensiunea superficiala
este echilibrata
de eforturi generate de proprietati specifice ale fluidelor ce se
manifesta numai pe interfata: (i) tensiunea superficiala ![]() (v. relatia (4.19)) sau gradientul tensiunii
superficiale pe interfata; (ii) elasticitatea de interfata (in
cazul fluidelor viscoelastice) sau (iii) a viscozitatii si
elasticitatii de interfata (cazul fluidelor imiscibile,
respectiv al lichidelor in care se gasesc surfactanti sau particule
deformabile, v. capitolul 1).
(v. relatia (4.19)) sau gradientul tensiunii
superficiale pe interfata; (ii) elasticitatea de interfata (in
cazul fluidelor viscoelastice) sau (iii) a viscozitatii si
elasticitatii de interfata (cazul fluidelor imiscibile,
respectiv al lichidelor in care se gasesc surfactanti sau particule
deformabile, v. capitolul 1).
In cazul ![]() , neglijand termenul cinetic in (11), se
obtine un rezultant important
, neglijand termenul cinetic in (11), se
obtine un rezultant important
![]() (23)
(23)
Deci, in lipsa transferului termic si considerand saltul de
temperatura nul, ![]() , diferenta dintre energia
interna a celor doua fluide (faze) aflate in contact genereaza o
putere mecanica la interfata. Conditia de salt pe
interfata devine importanta in acest caz si relativ la
principiul entropiei (5.25); cu
, diferenta dintre energia
interna a celor doua fluide (faze) aflate in contact genereaza o
putere mecanica la interfata. Conditia de salt pe
interfata devine importanta in acest caz si relativ la
principiul entropiei (5.25); cu ![]() si
si ![]() se obtine
se obtine
![]() (15)
(15)
unde ![]() defineste productia de entropie la
interfata.
defineste productia de entropie la
interfata.
Problemele devin cu mult mai dificile in cazul in care nu se cunoaste
forma interfetei, asa numitele probleme cu suprafata
libera. Majoritatea aplicatiilor practice de interes sunt in aceasta
categorie: evolutia picaturilor in aer si a bulelor in lichid,
transportul lichidelor suprapuse, jeturi libere, hidrodinamica filmelor
subtiri). In cazurile mentionate, pe langa rezolvarea
ecuatiilor de echilibru pentru fiecare fluid in parte si respectarea
conditiilor de salt mentionate, trebuie sa se aiba in
vedere ca relatiile (13) si (14) devin relatii de
inchidere, functia ![]() fiind aprioric necunoscuta.
fiind aprioric necunoscuta.
Dificultatile de calcul sunt majore, cu atat mai mult cu cat curgerile din aceasta categorie devin rapid instabile (impunerea unor ipoteze simplificatoare, cum ar fi cele de fluid ideal, lipsa tensiunii superficiale, miscare izocora si permanenta, neglijarea viscozitatii si elasticitatii de interfata, devine in acest caz o necesitate pentru obtinerea unor rezultate teoretice si numerice ). Studiile experimentale capata astfel importanta deosebita pentru rezolvarea unor probleme tehnice specifice, de exemplu: (i) forma suprafetei libere generate de rotatia corpurilor ; (ii) evolutia interfetei petrol-apa in conducte sub presiune ; (iii) stabilitatea curgerii jeturilor libere ; (iv) evolutia bulei cavitationale in vecinatatea peretilor ; (v) impactul picaturilor pe suprafete solide (v. figura 5); (vi) stabilitatea picaturilor la iesire din orificii (v. figurile 6 si 7).
b a



Fig. 5. Impactul unei picaturi
de fluid viscoelastic pe o suprafata solida.
Proprietatile fluidului (viscozitatea ![]() Pas, timpul de relaxare
Pas, timpul de relaxare ![]() s, densitatea
s, densitatea ![]() kg/m3, tensiunea superficiala
kg/m3, tensiunea superficiala ![]() N/m), diametrul echivalent al picaturii la impact d
= mm, viteza de impact Vi = m/s: a - impactul
picaturii pe suprafata solida (timpul dintre doua imagini
succesive
N/m), diametrul echivalent al picaturii la impact d
= mm, viteza de impact Vi = m/s: a - impactul
picaturii pe suprafata solida (timpul dintre doua imagini
succesive ![]() ms); b - evolutia picaturii dupa impact
(intervalul de timp dintre imagini
ms); b - evolutia picaturii dupa impact
(intervalul de timp dintre imagini ![]() ms) (experiment efectuat in Laboratorul
de
hidrodinamica,
Prof. C.
ms) (experiment efectuat in Laboratorul
de
hidrodinamica,
Prof. C.
Tropea, T. U. Darmstadt,


Fig. 6. Picatura
de sapun lichid in echilibru, la
iesirea dintr-un orificiu cu diametrul 2 mm ![]() = 1040 kg
/ m3,
= 1040 kg
/ m3,
tensiunea superficiala 0,0277 N/m).
![]()
![]()







Fig. 7. Evolutia unei picaturi de sapun lichid la iesirea in atmosfera dintr-un orificiu cu diametrul interior de 2 mm (experiment efectuat in Laboratorul de hidrodinamica,
Prof. H. Hampe, T. U. Darmstadt, Germania).
Chadwick, P., Continuum mechanics - concise theory and problems, George Allen & Unwin Ltd., London, p. 114, 1976
Ionescu, Gh. D., Mecanica fluidelor si masini hidraulice, Ed. Didactica si Pedagogica, Bucuresti, p. 125, 1983
Hutter, K., Fluid - und Thermodynamik, Springer Verlag, Berlin, p. 356, 1995
Scriven, L. E., Dynamics of a fluid interface, equations of motion for Newtonian surface fluids, Chem. Eng. Sci. 12, p. 98, 1960
Georgescu, Sanda Carmen, Evolutia unei bule: formarea la nivelul unui orificiu si spargerea la traversarea unei suprafete libere, Teza de doctorat, U.P.Bucuresti - I. N. P. Grenoble, 1999
Beavers, G. S., Experiments on free surface phenomena, J. Non-Newtonian Fluid Mech., 5, 323 - 352, 1979
Joseph, D. D., Chen, K. P., Renardy, Y. Y., Core - annular flows, Annu. Rev. Fluid Mech., 29, 65 - 90, 1997
Brujan, E-Al., Nahen, K., Schmidt, P., Vogel, A., Dynamics of laser - induced cavitation bubbles near an elastic boundary, J. Fluid Mech., 433, 251 - 281, 2001
|
Politica de confidentialitate |
| Copyright ©
2024 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |