
Asa cum am vazut anterior ecuatia legii a doua a termodinamicii este
![]() (16.51)
(16.51)
unde semnul = apare in cazul proceselor reversibile, semnul > fiind cel adecvat proceselor ireversibile. Prima aplicatie a legii a doua o vom prezenta prin definirea termodinamica a echilibrului. Am mentionat undeva pe la inceputurile discutiilor noastre ca echilibrul presupune ca nici una din variabile sa nu fie modificate in timp. O alta posibila definitie a echilibrului ar fi aceea ca toate variabilele ar avea o valoare corespunzatoare timpului egal cu infinitul. Nici una din aceste doua afirmatii nu ne permite insa sa exprimam echilibrul printr-o ecuatie matematica care sa poata analiza atent situatia echilibrului.
Legea a doua a termodinamicii ne ofera o definitie a echilibrului care o putem utiliza pentru a prezenta proprietatile sistemelor termodinamice la echilibru. Daca consideram acum un sistem inchis, izolat, deci dq = 0 si dV = 0, fapt care implica dU = 0. In aceste conditii ecuatia (16.51) devine
![]() (16.52)
(16.52)
Aceasta pare o forma simpla de exprimare dar in fapt este o expresie foarte profunda. Ea spune ca intr-un sistem inchis izolat (neperturbat din afara) orice schimbare spontana trebuie sa duca la cresterea entropiei.
Intr-un sistem inchis, izolat, entropia atinge valoarea maxima!
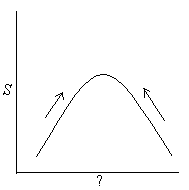
Daca vom reprezenta grafic variatia entropiei unui sistem inchis si izolat fata de una din variabilele sistemului orice modificare spontana trebuie sa conduca la o valoare maxima a entropiei. Daca sistemul nu este la echilibru atunci
![]()
dar daca sistemul este la echilibru orice modificare spontana in sistem trebuie sa lase entropia nemodificata,
![]()
Ecuatia (16.52) sta la originea uneia dintre cele mai extravagante si arogante afirmatii auzite vreodata "entropia universului creste continuu". Daca privim universul ca un sistem inchis si izolat, afirmatia ar fi probabil adevarata, chiar daca este dificil sa admitem o astfel de abordare a naturii universului.
Primul lucru pe care trebuie sa-l facem este sa incorporam noua noastra expresie gasita pentru legea a doua in ceea ce cunoastem deja. Mergand inapoi la legea intaia, considerand doar pV , putem scrie
![]() (16.53)
(16.53)
Daca restrictionam acum atentia doar asupra proceselor reversibile aceasta devine
![]() (16.54)
(16.54)
dar din legea a doua stim ca
![]() (16.55)
(16.55)
Combinand acum ecuatiile (16.53) si (16.54) vom ajunge la combinarea legii intaia cu cea de a doua
![]() (16.56)
(16.56)
(ulterior von considera si alt lucru pe langa pV ecuatiei (16.56)
![]() (16.57)
(16.57)
dar pentru moment ne vom limita la o considera la acesta.)
Ecuatia (16.56) indica ca variabile naturale ale energiei interne U sunt S si V. Anterior noi an considerat energia interna U drept functii de T si V ori de T si p, dar natura, prin expresia legii intaia si a celei de-a doua a termodinamicii, spune ca U este functie de S si V.
Daca acum impartim ecuatia (16.56) prin dT si mentinem constanta V, obtinem:
 (16.58 a, b)
(16.58 a, b)
Ecuatia (16.58 b) ne permite sa calculam modificarile de entropie pentr-o o anume clasa de procese, respectiv cele care se desfasoara la volum constant Sa determinam pentru ecuatia (16.58 b) integrala:
![]() (16.59)
(16.59)
si calculam modificarea de entropie pentru un proces care decurge la volum constant prin:
![]() (16.60)
(16.60)
Sa mergem mai departe cu incorporarea legii a doua in setul nostru de mijloace termodinamice, reamintindu-ne ca
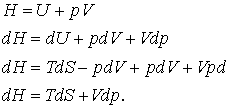 (16.61 a,b,c,d)
(16.61 a,b,c,d)
(de remarcat ca ecuatia (16.61 d) implica variabilele naturale pentru H pe S si p)
Sa divizam de data aceasta ecuatia (16.61 d) prin dT mentinand constant p
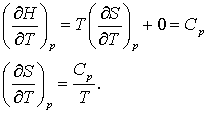 (16.62 a,b)
(16.62 a,b)
Putem utiliza ecuatia (16.62 b) pentru a calcula modificarile entropiei pentru procesele care decurg la presiune constanta. Sa pregatim aceasta ecuatie pentru integrare:
![]() (16.63)
(16.63)
si dupa integrare devine
![]() (16.64)
(16.64)
Dar care va fi situatia pentru un proces care se desfasoara la temperatura constanta T? Putem calcula modificarile entropiei pentru procesele care se desfasoara la T constant rearanjand ecuatia (16.55) pentru integrare,
![]() (16.65)
(16.65)
Modificarea finita a entropiei va fi
![]() (16.66)
(16.66)
Daca restrictionam acum pentru proces la temperatura constanta ecuatia (16.66) devine
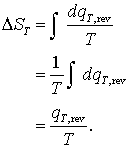 (16.67)
(16.67)
Sa se calculeze modificarea entropiei prin incalzirea a 1.oo mol aluminiu de la 300 K la 500K la presiune constanta. Capacitatea calorica la presiune constanta a aluminiului este data in buna aproximare de
![]()
Rezolvarea se obtine prin calcul prin
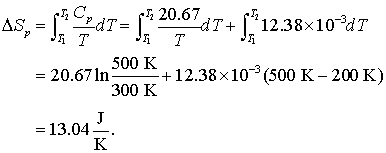
Exemplu de calcul pentru un proces reversibil
Adesea suntem nevoiti sa calculam modificarile de entropie in cazul proceselor reversibile. Noi nu stim cum sa calculam modificari ale entropiei in cazul proceselor ireversibile, dar ce conteaza! Entropia este o functie de stare deci ΔS nu depinde de drumul urmat. Tot ce trebuie sa ne imaginam este un drum reversibil care va afecta aceeasi modificare si de a calcula modificarea entropiei pentru acest drum reversibil.
Sa presupunem ca pornim cu doua blocuri de cupru, unul de 100 g la 500 k iar celalalt tot de 100 g dar la 300 k. Punand in contact termic cele doua bucati de cupru caldura se va deplasa de la bucata mai calda spre cea mai rece pentru egalarea temperaturii celor doua corpuri. Procesul este clar unul ireversibil. Sa ne imaginam totusi ca putem racii reversibil corpul mai cald la temperatura de egalizare precum si faptul ca putem incalzii reversibil bucata mai rece la aceeasi temperatura de egalizare. Vom calcula acum , pentru ambele procese modificarea de entropie conform din ecuatia (16.64). Modificarea totala a entropiei este tocmai suma celor doua modificari pentru fiecare proces in parte. De remarcat ca ne asteptam ca pentru acest proces valoarea modificarii entropiei sa fie una pozitiva deoarece procesul decurge spontan iar cele doua blocuri de cupru pot fi privite drept sisteme izolate.
Avem nevoie de urmatoarele valori
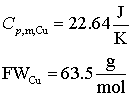
Trebuie intai sa determinam la ce temperatura finala se va ajunge. Putem face aceasta recunoscand ca energia (caldura) pierduta de blocul de caldura mai cald este acceptata de blocul de cupru mai rece. E ceea ce denumit noi "egalizarea caldurii"

Acesta se rezolva simplu si obtinem Tfin = 400 K. Deci:
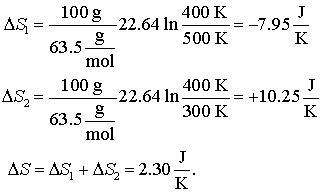
Inchipuiti-va ca avem un recipient impartit in doua compartimente. Intr-unul din acestea avem n1 moli ai gazului ideal 1, la presiune p si temperatura T. In celalalt compartiment avem n2 moli ai gazului ideal 2, la aceiasi p si T.
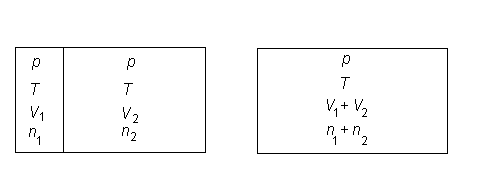
Daca eliminam obstacolul dintre cele doua compartimente, gazele difuzeaza si sistemul va atinge eventual o repartitie constanta a celor doua gaze in intreg recipientul. Acesta este clar un proces ireversibil astfel incat ne asteptam ca entropia sa creasca.
Pentru a calcula modificarea entropiei trebuie sa definim o cale reversibila pentru acest proces, chiar daca aceasta este o fictiune! Sa ne imaginam ca putem diviza procesul intr-unul care expandeaza unul din gaze reversibil si izoterm, fara a conturba de nici un fel comportarea celui de-al doilea gaz ideal.
Daca ne aducem aminte dU = 0 pentru expansiune izoterma a gazului ideal, atunci
![]() ( )
( )
astfel incat pentru un gaz ideal.
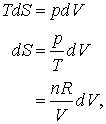 (16.69
a, b, c)
(16.69
a, b, c)
Astfel, pentru gazul ideal 1 considerat in fictiunea noastra ca avand o expansiune izoterma avem:
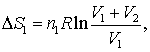 (16.70 a)
(16.70 a)
iar pentru gazul 2
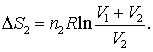 (16.70 b)
(16.70 b)
Deoarece modificarea entropiei reprezinta suma modificarilor entropiei celor doua procese
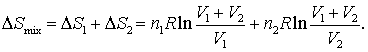 (16.71)
(16.71)
Ecuatia (16.71) poate fi folosita la calcule, dar nu este forma cu care suntem obisnuiti sa ne intalnim in astfel de situatii. Pentru obtinerea formei cu care suntem obisnuiti trebuie sa scoatem factor R in afara ecuatiei si sa inversam argumentul logaritmilor:
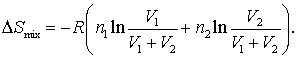 (16.72)
(16.72)
Deoarece facem calcule pentru gaze ideale, trebuie remarcat ca primul logaritm din ecuatia de mai sus devine
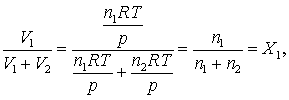 (16.73)
(16.73)
unde X1 este fractia molara a componentului 1. Exista o expresie echivalenta pentru expresia celui de-al doilea logaritm, iar entropia amestecului se poate scrie ca:
![]() (16.74)
(16.74)
Ecuatia (16.74) este de asemenea utila in calcule dar inca nu are forma standardizata. Pentru a obtine aceasta forma standardizata vom considera numarul total de moli n1 + n2 ca n si vom multiplica ultima ecuatie cu n. Vom obtine:
![]() (16.75)
(16.75)
care este aceeasi forma pe care o vom intalni atunci cand vom deriva expresia entropiei amestecurilor solutiilor ideale si aceeasi pe care Shannon a gasit-o pentru "entropia unui mesaj" ('entropy of a message') in seria faimoasa de articole asupra teoriei informatiei.
Daca cele doua gaze nu sunt la aceeasi presiune initiala vom fi nevoiti sa introducem cateva etape in plus. Expansiunea sau comprimarea unuia dintre gazele amestecului pentru al aduce la presiunea celui de-al doilea gaz, amestecarea gazelor, apoi comprimarea sau expansiunea amestecului pentru al aduce la volumul si presiunea finala corecta.
Daca cele doua gaze nu sunt la temperatura si presiune, situatia este si mai complicata. Trebuie sa determinam intai temperatura finala, prin utilizarea balantei de caldura, sa incalzim sau sa racim reversibil cele doua gaze pentru a ajunge ambele la aceeasi temperatura, sa le expandam sau comprimam, apoi sa le amestecam iar apoi acest amestec expandat sau comprimat sa fie adus la volumul corespunzator.
Ecuatia (16.75) poate fi usor extinsa pentru un amestec cu mai mult de doua gaze:
![]() (16.76)
(16.76)
Hai sa luam un exemplu pentru intelegerea problemei: entropia molara a aerului uscat. Compozitia aerului uscat este aproximativ 78% N2, 21% O2, si 1% Ar in procente volumice. Care va fi entropia molara amestecului din aerul uscat?
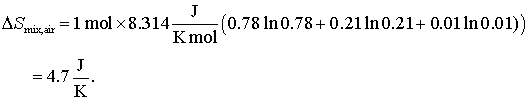
In mod cert entropia masoara dezordinea!
Daca vom observa procesele vom vedea care au o valoare pozitiva a entropiei si in consecinta o dezordine mai mare in acestea. Sa explicitam cateva din aceste observatii.
O expansiune izoterma va oferi moleculelor mai mult spatiu in jurul lor, deci moleculele sunt mai putin localizate.
Cresterea temperaturii determina cresterea vitezei medii a moleculelor si se spune ca moleculele sunt "mult mai dezordonate" in spatiul oferit.
Prin amestecarea gazelor (respectiv al lichidelor) intercalarea moleculelor determina evident o dezordine mai mare.
Modificarile de faza precum trecerea de la solid la lichid sau gaz, a unui lichid la gaz, duc la cresterea entropiei deoarece gazele sunt sisteme mult mai dezordonate decat lichidele sau solidele, iar lichidele sisteme mai dezordonate decat solidele.
De exemplu entropia de topire a 1.00 moli de gheata la 273,15 K (caldura de topire este 6.008 kJ/mol) va fi:
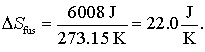
Vaporizarea lichidelor are o entropie pozitiva de valoare mare de vaporizare datorita "ordini" slabe care exista in sistemele gazoase. Benzenul spre exemplu are o caldura de vaporizare de 30.8 kJ la punctul de fierbere 353.1 K iar entropia de vaporizare este:
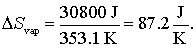
Ce este interesant este valoarea entropiei de vaporizare a multor substante la temperatura lor de fierbere care este in jurul valorii de 86 J/K, exceptie facand apa si heliul. Fenomenul este cunoscut sub denumirea de "regula lui Trouton". Pare usor de inteleasa aceasta regula daca se tine cont de faptul ca entropie reprezinta gradul de dezordine. Procesul de vaporizare creeaza un ansamblu egal de numar de particule dar mult mai dezordonate decat intr-un sistem lichid sau solid. Toate gazele considerate sunt la o presiune de una atmosfera, fiind considerate la temperatura lor normala de fierbere.
|
Politica de confidentialitate |
| Copyright ©
2024 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |