Toate gazele reale se pot lichefia. In functie de gaz aceasta va necesita comprimare si/sau racire. Exista totusi, pentru fiecare gaz, o temperatura peste care acesta nu mai poate fi lichefiat. Aceasta temperatura a fost definita drept temperatura critica fiind de obicei simbolizata prin Tc. In consecinta pentru a lichefia un anume gaz real temperatura acestuia trebuie sa fie egala sau sub valoarea temperaturii critice.
Exista gaze, denumite "gaze permanente" a caror temperatura critica este sub temperatura camerei. Aceste gaze trebuiesc racite la temperaturi sub temperatura lor critica atunci cand se lichefiaza. Exemple de "gaze permanente": He, H , N , O , Ne, Ar, si asa mai departe. Multe substante au temperaturi critice peste temperatura camerei. Aceste substante lichide (sau chiar si solide) la temperatura camerei. Spre exemplu apa are temperatura critica la 647.1 K, temperatura mult mai inalta decat standardul temperaturii camerei 298.15 K. Apa poate fi lichefiata la orice temperatura sub 647.1 K (desi peste 398.15 K - temperatura normala de fierbere a apei - trebuie aplicata o presiune mai mare ca cea atmosferica pentru a pastra apa in forma lichida)
O imagine simpla asupra acestor substante lichefiabile si a fenomenelor critice o poate reprezenta diagrama p-V. Aceasta nu este altceva decat graficul rezultat la plotarea presiunii p pe axa verticala ca functie de volum V, reflectat in axa orizontala. Daca vom reprezenta presiunea unui substante in functie de volum, atunci cand mentinem sistemul la o temperatura anumita, constanta, atunci pentru fiecare temperatura vom obtine o curba definita drept izoterma volum Este un inconvenient sa consideram substantele lichefiabile si fenomenele critice doar utilizand diagrama p-V.
Un exemplu de astfel de curbe este reprezentat intr-un fisier Excel care contine sase izoterme pentru ecuatia de stare van der Waals (temperaturile la care s-au facut determinarile sunt reprezentate in randul de sus iar volumele in primele coloane din stanga. Temperaturile sunt reprezentate comparativ cu temperatura critica astfel incat temperatura la valoarea 1.0 este temperatura critica, temperatura la valoarea 1.1 este peste cea critica si asa mai departe. Izotermele determinate la temperaturi sub cea critica, de exemplu la valoarea 0.9 sunt specifice ecuatiei de stare van der Waals dar nu sunt fizic realiste. In fisierul EXCEL asociat puteti face singuri modificari ale temperaturii pentru a observa modificarea izotermelor.)
De remarcat ca atunci cand o substanta este lichefiata izoterma incepe sa fie "aplatizata", adica panta curbei devine zero. La izoterma critica panta "se apropie" de aplatizare la un anumit punct al graficului. Un punct la care functia descrescanda devine plata inainte de a descreste este denumit punt de inflexiune. Caracteristica matematica a punctului de inflexiune este ca prima si a doua derivata sunt zero pentru aceasta valoare. Pentru izoterma noastra critica intr-o reprezentare p-V putem scrie in consecinta:
![]() , (5.1)
, (5.1)
si
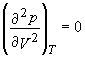 (5.2)
(5.2)
Ecuatiile (5.1) si (5.2) constituie un set de ecuatii cu doua necunoscute, V si T. Acum putem testa daca o ecuatie de stare se apropie semnificativ de valoarea punctului critic prin calcularea acestor doua ecuatii pentru ecuatia de stare precum si rezolvarea celor doua derivate. Daca exista o solutie (si p si V nu sunt nici zero, nici infinit) putem spune ca ecuatia de stare are un punct critic.
Sa folosim acest test pentru a vedea daca gazul ideal are un punct critic. In primul rand trebuie sa rezolvam ecuatia de stare a gazului ideal. Din PV = nRT, pentru o presiune, p, exprimam valoarea lui p
![]() (5.3)
(5.3)
Acum urmeaza sa luam cele doua derivate reprezentate prin ecuatiile (4.9) si (4.10) si sa le egalam fiecare cu zero. (uneori multi dintre noi sunt tentati sa considere cele doua derivate egale cu zero. Nu este nimic rau in asta, atata doar ca acum vom avea o singura ecuatie cu doua necunoscute. Mult mai multe informatii avem daca vom egala fiecare din aceste derivate cu zero decat daca le egalam!)
![]() (5.4)
(5.4)
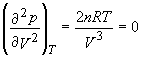 . (5.5.)
. (5.5.)
Este usor de observat ca cele doua ecuatii sunt satisfacute daca T = 0, sau V = ∞. Nici una din aceste solutii nu sunt satisfacatoare din punct de vedere fizic iar concluzia care se desprinde este ca pentru gazul ideal nu exista un punct critic!
Ce ar fi sa incercati chiar voi daca
ecuatia de stare aproximativa, ![]() , are un punct
critic sau nu, sau sa verificati daca ecuatia de stare van
der Waals are un punct critic, respectiv sa determinati constantele
critice VC , TC si pC
, are un punct
critic sau nu, sau sa verificati daca ecuatia de stare van
der Waals are un punct critic, respectiv sa determinati constantele
critice VC , TC si pC
|
Politica de confidentialitate |
| Copyright ©
2024 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |