MODEL-MODELARE
Simularea inlocuieste sistemul de studiat folosind o alta forma de reprezentare care se numeste model.
Un model este o descriere - intr-o forma bine definita - a anumitor comportari ale sistemului cu scopul de a prognoza o serie de comportari viitoare pentru seturi de I/ si perturbatii.
In mod virtual orice model util simplifica si idealizeaza realitatea, adesea limitele unui sistem si model sunt mai mult arbitrar definite.
Pentru a obtine un model usor de manipulat, o serie de elemente care actioneaza asupra sistemului trebuie neglijate pe baza unei prioritati apriori, chiar daca nu se poate demonstra riguros ca ce a fost neglijat este nesemnificativ. Pentru ca un model sa fie util este esential sa se defineasca un sistem-limita si rezonabil de descriptori.
Un prim beneficiu al efortului modelarii este ca influenteaza o mai buna intelegere asupra fenomenelor care au loc la nivelul sistemului real.
De mentionat faptul ca primul pas in studiul unui sistem sau proces -este realizarea unui model, care poate sa fie fizic la alte dimensiuni sau o formalizare matematica a comportarii sistemului de studiat.
Complexitatea si diversitatea sistemelor si proceselor tehnologice din ultimele doua decade au condus la necesitatea elaborarii unor modele foarte variate, care pot fi clasificate dupa diverse criterii. Daca se tine seama de faptul ca simularea este o tehnica utilizata pentru a investiga comportarea unor sisteme complexe ce sunt supuse unui numar mare de restrictii, atunci modelele utilizate in simulare trebuie sa satisfaca cateva cerinte de baza:
. sa serveasca intelegerii configuratiei sistemului, nu numai in reprezentarea formalizata a componentelor sale, dar sa reprezinte in mod riguros si interactiunile dintre acestea. De asemenea configuratia sistemului sa fie usor modificata prin ajustarea unor parametri sau variabile.
. sa permita modificari in regim dinamic pentru un nou algoritm de alocare a resurselor sau de planificare in luarea unor decizii riguroase. Modelul trebuie sa raspunda prompt si exact la schimbarea unor elemente de I/ sau stare in comportarea sistemului.
. sa serveasca drept mijloc pentru determinarea efectelor unor serii de I/ (intrari) relativ la incarcarea sistemului, la comportarile sale interioare, analizele efectuandu-se asupra (iesiri) /E din sistem, care reflecta reactiile sistemului pentru setul de I/ generate.
Un model continuu este descris printr-un sistem de ecuatii algebrice sau diferentiale in care variabilele reprezinta atributele entitatilor iar functiile reprezinta activitatile. Astfel de modele se pot simula cu ajutorul calculatoarelor analogice sau numerice.
In principal modelele discrete iau forma unui set de numere care reprezinta entitatile si indica starea lor. Ecuatiile logice sau probabilistice controleaza momentele la care apar schimbarile de stare in cadrul sistemului prin analiza rezultatelor de /E/ (iesire).
Din punctul de vedere al simularii distinctia intre aspectul continuu si cel discret iese in evidenta mai mult la nivelul modelului, decat la cel al sistemului de studiat.
Activitatea de modelare ofera analistului o serie de facilitati cum ar fi:
- asigura un grad de certitudine asupra unor ipoteze facute intuitiv sau prin observatii empirice asupra sistemului si sa deduca o serie de implicatii logice ;
- conduce la imbunatatirea intelegerii sistemului;
- da posibilitatea unor detalieri si adanciri a cunoasterii unor subsisteme ce alcatuiesc sistemul considerat;
- permite observari cu rapiditate a raspunsurilor sistemului la modificari ale /I/ (intrari);
- modelul este mai usor de manipulat decat sistemul real;
- studiul sistemului implica un cost mai redus;
- permite sesizarea mai multor surse care genereaza tranzitii de stare pentru sistem decat sistemul real analizat etc.
Dupa natura elementelor ce le alcatuiesc se disting trei mari tipuri de modele, care pot fi exacte (ce produc solutii exacte) sau modele aproximative (care produc o solutie ce difera de solutia exacta, functie de gradul de aproximare):
- Modelele fizice ale caror elemente sunt de natura fizica machete, tunele de incercari, avioane, simulatoare, machete de instalatii tehnologice;
- Modelele abstracte sunt modele in care variabilele descriu entitatile, iar functiile care le contin descriu activitatile si legaturile intre diferite componente;
- Modelele hibride sunt acelea care imbina caracteristicile primelor doua adica, contin si componente ale sistemului real, intr-o conexiune cu un calculator numeric pe care se ruleaza programul de simulare al modelului abstract.
Procesul de modelare are la baza doua obiective esentiale:
- modelul trebuie sa reprezinte cat mai precis sistemul considerat sau cel putin caracteristicile sale esentiale (sau critice);
- modelul sa fie ieftin, sau usor de manipulat fata de sistemul original.
Ultimul obiectiv uneori are un rol mai mare si acest lucru se realizeaza in dauna preciziei.
Pentru atingerea celor doua obiective ale modelarii si tinand seama de natura sistemelor si proceselor de modelat, modelele pot fi:
. analogice, ce utilizeaza un set de proprietati fizice de o anumita natura pentru a reprezenta alte proprietati fizice de alta natura ;
. simbolice sau matematice, in care atributele fizice ale sistemului sunt notate printr-un set de variabile, iar relatiile intre variabile, prin functii matematice exprimate cantitativ sau logic;
. iconice, ce reprezinta direct sistemul (la alte dimensiuni) sau imaginea sistemului real (harta unei tari, tren miniatura, racheta in miniatura etc.). Structura modelului. iconic si a celui simbolic nu se exclud, ba mai mult, pot fi utilizate simultan.
Marimile de intrare intr-un sistem real pot lua diverse forme si reprezentari, functie de natura sistemului.
La constructia modelului sistemului apar urmatoarele intrebari la care trebuie dat un raspuns:
. Ce tehnica de proiectare va fi utilizata? iconica sau simbolica, sau ambele. Este de mentionat ca:
. modelele iconice dau rezultate foarte precise si se construiesc rapid, dar necesita un timp calculator destul de mare si sunt foarte greu de parametrizat ;
. modelele simbolice, au in general, un timp de rulare caracteristic si sunt mult mai flexibile.
Abordarea ierarhica care utilizeaza ambele tehnici in procesul modelarii reprezinta un compromis util, in sensul ca acele componente ale sistemului critice sau cele la care este dificil sa li se asigure probabilitati vor fi tratate iconic, iar celelalte vor fi modelate simbolic.
. La ce nivel de detaliu sau rezolutie se va merge cu simularea, in acest caz se prefera o abordare la nivel mixt, in care submodelele au grade diferite de rezolutie.
. Cat de mult poate un model sa fie simplificat fara o pierdere deosebita in directia preciziei?
. Ce metode vor fi utilizate pentru constructia modelului? Metodele existente includ diversele limbaje de simulare, modelele speciale si pachetele de simulare de interes general.
. Cum poate fi un model validat? In general se folosesc tehnicile analitice pentru a demonstra ca rezultatele simularii sunt fezabile. Iar daca sistemul modelat exista fizic, este controlat si masurat utilizand modelul calibrat.
In cadrul simularii sistemelor trebuie facuta o distinctie intre: modelele pentru sisteme discrete si cele pentru sisteme continue. Exemplu de model discret poate fi dat de analiza traficului unor entitati discrete, cum ar fi deplasarea autocamioanelor intre depozite, unde in final se simuleaza in mod gradat schimbari in compozitie sau stare ale unei multimi de agregate.
Modelarea proceselor continue in general consta dintr-un numar de ecuatii diferentiale, care in general se pot rezolva cu ajutorul unui calculator analogic, in ultimii ani insa au fost utilizate din ce in ce mai mult calculatoarele numerice.
Simularea sistemelor continue pe
calculatoarele numerice este numita uneori modelare in pasi de timp,
deoarece ea avanseaza prin cresterea timpului cu un interval ![]() , schimbarile
de stare fiind calculate la fiecare pas
, schimbarile
de stare fiind calculate la fiecare pas ![]() Simularea
sistemelor cu ajutorul calculatoarelor implica o varietate de evenimente,
in cadrul acestei categorii de sisteme se intalnesc doua subdiviziuni,
intre care trebuie sa se faca o distinctie in functie de
natura intrarilor:
Simularea
sistemelor cu ajutorul calculatoarelor implica o varietate de evenimente,
in cadrul acestei categorii de sisteme se intalnesc doua subdiviziuni,
intre care trebuie sa se faca o distinctie in functie de
natura intrarilor:
- in prima, intrarile sunt generate aleator cu ajutorul unei distributii probabilistice (simulare stocastica) pe cand in alte situatii sunt prezentate ca o secventa de etape de lucru, natura fiecareia dintre ele fiind explicit definita (simulare determinista);
- in a doua diviziune se includ modelele de simulare rezultate, in urma instructiunilor obtinute prin control (monitoring); astfel de modele sunt adesea numite emulatoare.
In acest context termenul de "emulator' are anumite limite in sensul utilizarii, de exemplu, in tehnica de calcul el se refera la facilitatile software sau de microprogramare, care permit unui program realizat pentru a fi rulat pe un anumit calculator sa poata fi executat corect si fara modificari pe un alt calculator. Astfel de emulator poate fi privit ca un caz special al formei generale in care procesele simulate sunt la cel mai redus nivel posibil, in acest sens se poate spune ca orice model al unui sistem de calcul se poate divide in doua parti: modelul de incarcare al sistemului de calcul si modelul propriu-zis al sistemului.
La realizarea modelului de simulare, ambele aspecte (incarcarea sistemului si sistemul propriu-zis) trebuie tratate la fel de riguros.
In primul rand apar dificultati inerente in descrierea modului de incarcare a sistemului, chiar daca observarile rezulta prin monitoring pentru a determina intrarile in sistem, de unde rezulta necesitatea ca cel care realizeaza modelarea sa fie satisfacut de modul in care tehnica monitoring descrie incarcarea sistemului.
Dupa cum se observa din literatura, modelarea analitica nu este o varianta in procesul de simulare a comportarii sistemelor pentru anumite circumstante, ci din contra reprezinta un instrument indispensabil in realizarea simularii insasi.
Exista modele analitice care pot fi rezolvate cu sau fara ajutorul calculatorului. De asemenea se utilizeaza dispozitive electrice, hidraulice, mecanice sau numerice analoage cu elementele sistemului, astfel putandu-se realiza un calculator analogic dedicat sistemului considerat.
Proiectantul poate cu aceste mijloace analogice sa introduca diverse conditii initiale si sa traseze functiile de /E si sa aiba de multe ori aceleasi informatii pe care le obtine prin mijloace pur matematice.
Indiferent de mijloacele de calcul utilizate etapele sunt in mare masura aceleasi:
- enuntarea corecta a problemei de rezolvat, definirea parametrilor dominanti ;
- constructia unui model matematic folosind abstractizarea si o reprezentare simplificata a sistemului;
- rezolvarea ecuatiilor modelului matematic prin mai multe mijloace apropiate, analitic sau experimental;
- verificarea sistemului, masurarea parametrilor, si/sau testarea modelului, pentru a vedea daca sunt obtinute rezultate corespunzatoare.
1.2. ETAPELE MODELARII UNUI SISTEM
Activitatea de modelare a sistemelor si proceselor implica o serie de etape, ce difera intre ele in functie de natura sistemului sau a procesului:
Formularea temei in majoritatea cazurilor un analist nu poate fi niciodata sigur ca tema sau problema de rezolvat este corect formulata si admite solutie. Mai mult, el este de la inceput sigur ca pe parcursul modelarii va descoperi o serie de erori in formularea temei, dupa un numar de examinari repetate. Formularea corecta a temei implica studii laborioase pentru a intelege cat mai bine legile dupa care sistemul va evolua si care sunt trasaturile esentiale ce-1 caracterizeaza.
In urma unor serii de testari apare necesitatea concentrarii asupra a ceea ce este nou si caracteristic in faza de formulare a problemei prin a da raspuns la urmatoarele intrebari: ce informatii contine tema formulata?, ce este caracteristic mediului in care a fost formulata tema?, care sunt mijloacele ce urmeaza a fi folosite pentru formularea problemei ? Aceasta etapa dureaza mai mult sau mai putin, in functie de cunostintele si experienta analistului.
Identificarea variabilelor relevante din sistem si reperarea lor prin intermediul analizei si descompunerii sistemului in subsisteme in cazul in care un analist intalneste o tema noua, straina preocuparilor trecute, este posibil sa comita o serie de confuzii in momentul initial, dar daca dispune de experienta si cunoaste intr-o anumita masura sistemul de studiat atunci o serie de ipoteze emise pot avea sens. Atat etapa de formulare a temei, cat si cea de identificare si reperare a variabilelor implica din partea analistului cunostinte profunde in domeniu si experienta pentru a realiza un model care sa reprezinte cat mai fidel sistemul de simulat.
Abordarea in flux Cea mai folosita metoda de analiza este cea in flux a sistemului incepand de la I/ spre /E, a elementelor principale de studiat.
Este evident ca in urma unor observari secventa de etape in sistem poate fi privita ca o variatie de stari si momente de trecere de la una la alta realizata in momentul urmator.
Analiza in flux evidentiaza in mod riguros modul in care evolueaza spatiul starilor sistemului de studiat.
In mod natural daca se foloseste analiza in flux grupul de procese ce au loc la nivelul sistemului trebuie tratate sub forma de subsisteme, prin descompunerea sistemului de studiat. Dupa ce a reusit sa inteleaga o serie de lucruri despre sistemul de studiat utilizand analiza in flux analistul poate identifica subsistemele care-1 formeaza.
Abordarea functionala Dupa cele trei etape prezentate analistul detine toate informatiile pentru a defini functiile ce descriu evolutia sistemului studiat, in continuare se initiaza procesul de modelare al sistemului si procedurile prin care fiecare functie poate fi reprezentata in scopul furnizarii informatiilor asupra evolutiei sistemului realizat.
Analiza schimbarilor de stare in aceasta etapa se efectueaza o serie de listari folosind diverse seturi de marimi de I/ si stimuli, pentru a analiza informatiile de /E in ideea de a observa daca sistemul modelat satisface cerintele temei enuntate si raspunde restrictiilor impuse. Cu alte cuvinte, este faza in care modelului i se aduc o serie de corectii pentru a obtine sistemul dorit (in cazul cand el nu exista) sau se imbunatatesc performantele unuia deja existent.
1.3. MODELELE SI CLASIFICAREA LOR
Constructia modelelor asociate proceselor si sistemelor este o latura esentiala a procesului de simulare, fiind absolut necesara o distinctie intre diferitele tipuri de modele ce pot fi folosite de catre analisti. O clasificare a tipurilor de modele serveste la clasificarea tehnicilor de simulare si a examinarii relatiilor ei cu alte discipline.
Procesul de modelare poate fi considerat ca alcatuit din doua etape: una care specifica forma in care modelul trebuie exprimat; iar a doua prin care se descrie modul cum el este utilizat pentru a furniza o serie de predic-tii sau sa ofere solutia optima a problemei studiate. Nu trebuie insa neglijati unii factori foarte importanti in evaluarea metodelor de modelare, cum ar fi: costul relativ al utilizarii acestor modele (eficienta lor), usurinta cu care ele pot fi transmise de la cei ce le-au realizat la cei ce le aplica, facilitati de manipulare, gradul de precizie oferit, limitele in care pot fi aplicate modelele respective.
Pe baza criteriilor de alegere intre diverse tipuri de modele, se utilizeaza mai frecvent in practica urmatoarele modele: descriptive, fizice, matematice, procedurale.
Modelele descriptive - care sunt exprimate in limbajul natural au foarte multe limitari, avantajul lor fiind costul redus in procesul de prognozare, fapt care a facut sa fie inainte foarte utilizate dar predictiile facute erau foarte probabile, deci precizia extrem de scazuta.
Modelele fizice variaza foarte mult in complexitatea lor, iar metodele de optimizare a celor fizice implica o cercetare a diverselor alternative de proiectare dupa urmatoarele etape:
- stabilirea criteriilor de performanta;
- estimarea unor combinatii initiale privind variabilele controlabile;
- modelul este atunci utilizat pentru a prognoza valoarea - gasirea unui criteriu de performanta tinand seama de conditiile impuse;
- utilizarea unei metode de analiza care incorporeaza toate rezultatele si datele, atribuite variabilelor controlabile.
Metoda de analiza este proiectata astfel incat sa deplaseze variabilele controlabile in directia ce va conduce la o mai mare imbuna latire a performantelor.
In momentul atingerii performantelor maxime (metoda de analiza a gasit un optim) atunci valorile variabilelor controlabile care au condus la acea stare reprezinta conditiile de operare dorite.
Un avantaj semnificativ al modelelor fizice este usurinta cu care sunt primite si intelese de cei ce nu au pregatire adecvata domeniului, dar din punctul de vedere al procesului de luare a deciziei ele sufera de incapacitatea de a reprezenta procesele informationale. Mai mult decat acest dezavantaj, modelele fizice implica un cost mare si, de obicei, modelul poate fi utilizat numai in scopul particular pentru care a fost proiectat.
Modelele matematice Cercetarile operationale, ca si alte discipline de cercetare, au progresat prin utilizarea modelelor simbolice, ce folosesc intr-un mod concis notatii matematice, pentru a reprezenta starile variabile din sistem si sa descrie modul in care variabilele se schimba si interactioneaza intre ele.
Predictiile privind comportarea sistemului se fac cu ajutorul reprezentarilor simbolice, prin intermediul procedurilor matematice. O importanta cerinta a modelelor simbolice consta in alegerea adecvata a structurii formale de axiome, teoreme si proceduri.
Costul utilizarii modelelor simbolice este adesea destul de redus. Axiomele, teoremele si procedurile matematice dau de asemenea posibilitatea ca o serie de proprietati generale ale sistemului cat si predictiile sa poata fi deduse si specificate.
In foarte multe cazuri modelele matematice sunt modele continue. Pentru a putea fi prelucrate pe un calculator numeric ele trebuie impuse unui proces de discretizare obtinandu-se o solutie aproximativa. O precizie buna pentru solutie necesita un pas de discretizare mic si deci un volum mare de calcule care conduce la un timp calculator mai mare si deci un cost ridicat.
Pentru rezolvarea aceleiasi probleme exista diverse metode numerice aproximative ce pot oferi posibilitatile de a compara rezultatele.
Se poate da urmatorul exemplu-privind aproximarea numerica a integralei prin doua metode:
- aproximarea iterativa folosind metoda trapezelor (sau alta metoda) bazata pe faptul ca integrala definita reprezinta aria cuprinsa intre graficul lui f (x) si dreptele x = a, x = b respectiv axa OX;
- aproximarea cu ajutorul metodei Monte Carlo; acest al doilea mod de aproximare foloseste informatii ca probabilitatea de aparitie a unor evenimente poate fi exprimata ca o integrala si integrala se exprima printr-un proces discret de distributie probabilistica.
Modelele procedurale care - in general - sunt folosite direct ca simulare. De aceasta data modelul este o procedura exprimata in simboluri precise, iar termenul de simulare se refera la metoda utilizata in realizarea predictiilor asupra evolutiei sistemului sau procesului.
Modelul procedural reprezinta relatiile dinamice presupuse prin ipoteza ca exista in cadrul procesului real, folosind o serie de operatii elementare intre variabilele corespunzatoare. De obicei aceste operatii sunt asemanatoare unei diagrame logice dar adesea pot fi prezentate sub forma unor tabele de decizie, sau prin intermediul unor limbaje procedurale.
Calculele implicate de model se executa pe un calculator, el fiind programat sa execute operatiile implicate de procedura (care de fapt este modelul), rezultatul obtinut constituie sistemul de predictii. Cu alte cuvinte, se poate afirma ca simularea este un model al unui proces sau sistem in care componentele sale sau starile procesului sunt reprezentate prin operatii aritmetice si logice intre variabilele si parametrii dominanti care determina tranzitiile de stare ale procesului sau sistemului ce poate fi executat pe un calculator in scopul predictarii dinamice a comportarii procesului sau sistemului considerat. Trebuie mentionat faptul ca datorita structurii proceselor sau a sistemelor tipurile de modele care nu utilizeaza explicit formalizarea matematica, combinarea optima a variabilelor controlabile trebuie realizata prin procese de cercetare sau prin alte metode, de asemenea in cazul in care modelul are o solutie analitica care poate fi gasita, simularea nu mai este necesara.
Simularea este o metoda relativ costisitoare. Ea presupune parcurgerea fazei de modelare a procesului sau sistemului (care poate fi redus prin utilizarea unui limbaj de simulare adecvat) si folosirea calculatorului un timp relativ mare pentru a gasi predictiile dinamice optime privind comportarea viitoare a procesului sau sistemului.
In analiza, unui sistem se cere determinarea prin calcul a indicatorilor de performanta ai sistemului dat. Aceasta presupune cunoasterea modelului matematic al sistemului, adica a relatiilor dintre marimile de iesire si marimile exogene. Modelele matematice ale sistemelor (proceselor) se pot obtine in principal prin doua metode distincte:
- prin modelare analitica,
- prin identificare experimentala.
Modelarea analitica permite deducerea modelului matematic pe baza datelor de proiectare privind sistemul examinat, fara ca acesta sa fie fizic disponibil. Cunoscand structura si parametrii sistemului, intr-o faza preliminara realizarii fizice a acestuia, se poate stabili - prin modelare analitica (teoretica).
modelul matematic al sistemului si, pe aceasta baza, se pot deduce, anticipativ, performantele sistemului.
Identificarea experimentala consta in stabilirea modelului matematic pe baza prelucrarii datelor de intrare - iesire masurate in cadrul sistemului analizat. Identificarea experimentala a unui sistem presupune, existenta fizica a acestuia si realizarea unui experiment prin care se obtine inregistrarea marimilor de intrare - iesire. Pe aceasta cale se obtin modele matematice care concorda in mai mare masura cu sistemul examinat, decat cele rezultate prin modelare analitica. Deseori se imbina cele doua cai de obtinere a modelelor matematice: prin modelarea analitica (teoretica) se stabilesc anumite proprietati calitative ale sistemului si structura modelului matematic, iar prin identificare experimentala se precizeaza parametrii incerti din model.
1.4.1 Notiuni introductive
Exprimarea matematica a legaturii dintre marimile de iesire si de intrare din sistem se poate face prin modele foarte variate. Trebuie precizat ca din multimea formelor de reprezentare a modelelor matematice, sunt foarte importante doua tipuri de modele:
- modele functionale sau de tip intrare - iesire, care se exprima prin ecuatii diferentiale ce leaga direct marimile de functionare ale sistemului, adica marimile de intrare si de iesire;
- modele structural - functionale sau de tip intrare -stare -iesire care dau si unele informatii suplimentare asupra structurii sistemului. Variabilele de intrare sunt legate prin ecuatii diferentiale de variabilele de stare, care caracterizeaza fenomenele de acumulare de substanta si/sau energie din sistemul fizic modelat. Marimile de iesire sunt determinate univoc, prin relatii algebrice, de variabilele de stare ale sistemului.
Modelarea analitica are ca obiectiv obtinerea modelului structural functional al unui sistem dat.
Pentru stabilirea modelului analitic al unui sistem se modeleaza fiecare element component al sistemului si apoi se cupleaza ecuatiile elementelor in cadrul unui model matematic unitar, al intregului sistem.
1.4.2. Modelarea matematica a instalatiilor
Instalatiile tehnologice pot fi de o mare varietate, chiar si in cazul unui singur profil tehnologic (de exemplu; tehnologiile metalurgice). Deducerea ecuatiilor diferentiale ce leaga marimile de iesire, pe de o parte, de marimile de executie si perturbatoare, pe de alta parte, este o operatie dificila si necesita doua categorii de cunostinte :
1 - privind metodologia modelarii matematice a proceselor;
2 - cunostinte de specialitate, in domeniul proceselor care stau la baza functionarii instalatiei tehnologice.
In cele ce urmeaza se accentueaza asupra metodologiei modelarii matematice a instalatiilor tehnologice.
1.4.3. Metodologia modelarii matematice analitice
Stabilirea corecta a modelelor matematice ale instalatiilor tehnologice, presupune parcurgerea armatoarelor etape :
Stabilirea
"conturului' obiectului modelat si a marimilor de intrare -
iesire. Fie IA1
instalatia care, intr-o prima analiza, s-a considerat obiectul
modelarii matematice. Se stabilesc, pentru IA1, marimile
de intrare preliminare, cat si marimile ce constituie variabile
dependente (de iesire). Se examineaza, pentru fiecare intrare din
lista preliminara, instalatia exterioara ce furnizeaza
marimea de intrare respectiva. Daca marimea de intrare
preliminara uk(t) este data de instalatia IA2
care primeste la intrare o variabila, dependenta (de iesire) din
IA1, atunci IA1 si IA2 trebuie modelate
si analizate ca un sistem unitar (fig. 1.1). "Conturul" obiectului modelat
se largeste succesiv, de fiecare data cand se constata
ca o intrare provine de la un sistem exterior, ![]() , ce este excitat de o iesire a obiectului. In noul contur va fi
inclus si sistemul, dupa care se examineaza in continuare, in
acelasi mod, intrarile noului obiect modelat, ce cuprinde si pe
, ce este excitat de o iesire a obiectului. In noul contur va fi
inclus si sistemul, dupa care se examineaza in continuare, in
acelasi mod, intrarile noului obiect modelat, ce cuprinde si pe ![]() . In final, marimile de intrare (exogene) ale obiectului
modelat extins se considera ca atare daca sistemele exterioare care
le furnizeaza nu primesc la intrare variabile de iesire din obiectul modelat.
. In final, marimile de intrare (exogene) ale obiectului
modelat extins se considera ca atare daca sistemele exterioare care
le furnizeaza nu primesc la intrare variabile de iesire din obiectul modelat.
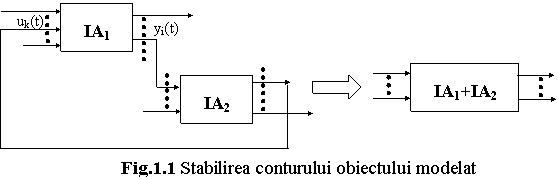
Ca rezultat al primei etape, se obtin urmatoarele informatii :
- structura obiectului modelat extins, care cuprinde subsisteme ce interactioneaza; printre acestea se afla si instalatia IA1, de la care s-a pornit intreaga procedura de analiza;
- marimile exogene (de executie si perturbatoare) si de iesire, corespunzatoare obiectului modelat.
In continuare, celelalte etape ale metodologiei de modelare se aplica succesiv fiecarui subsistem din structura obiectului modelat. Prin cuplarea modelelor matematice ale subsistemelor se obtine modalul matematic al obiectului extins, reprezentand instalatia ce trebuie considerata in analiza sistemului.
Stabilirea ecuatiilor de stare din modelul matematic.
Este etapa cea mai importanta si mai dificila, necesitand analiza proceselor din instalatie, din punctul de vedere al dinamicii instalatiei automatizate.
Ecuatiile de stare sunt ecuatii diferentiale de ordinul intai, care provin din relatii de bilant material sau energetic, unde se considera variatia acumularii de masa respectiv energie. Variabilele care apar derivate in ecuatiile de stare se numesc variabile de stare.
Se vor prezenta cateva forme de ecuatii de bilant, care pot reprezenta ecuatii de stare in modelul instalatiei analizate.
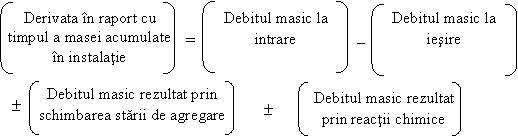
I. Ecuatia de
bilant material
a)

in procesele
mecanice:
b)

in procesele electrice:
c)
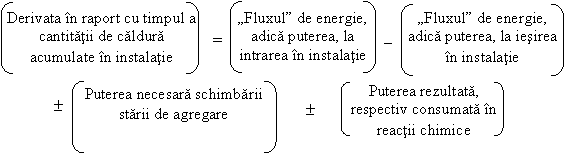
in procesele de
schimb de caldura
Pentru stabilirea corecta a ecuatiilor de stare ale instalatiei modelate, este necesar sa se aiba in vedere urmatoarele aspecte :
a). Daca acumularile de substanta sau energie sunt mici, efectele dinamice produse de variatiile acestor acumulari sunt ne -semnificative si in ecuatiile de bilant respective se considera egal cu zero termenul din partea stanga* Ecuatiile de bilant capata, in acest caz, forma algebrica utilizata curent la tratarea in regim stationar a proceselor din instalatie.
b). Fie x1, x2, ., xn
variabilele de stare, adica marimile ce apar derivate in
ecuatiile de bilant cu acumulari variabile. Numarul n al
variabilelor de stare reprezinta ordinul sistemului de ecuatii
diferentiale ce formeaza modelul matematic. Vectorul ![]() numit vector de stare,
caracterizeaza dinamica instalatiei, obtinuta prin modelul
matematic al acesteia. Pentru ca acest model sa reflecte cat mai bine
procesele dinamice reale din instalatie, este necesar ca ordinul
sistemului sa fie astfel ales, incat sa corespunda
acumularilor ce produc efecte semnificative in dinamica instalatiei,
fara a include - totusi - acumularile minore, care
complica in mod inutil modelul matematic.
numit vector de stare,
caracterizeaza dinamica instalatiei, obtinuta prin modelul
matematic al acesteia. Pentru ca acest model sa reflecte cat mai bine
procesele dinamice reale din instalatie, este necesar ca ordinul
sistemului sa fie astfel ales, incat sa corespunda
acumularilor ce produc efecte semnificative in dinamica instalatiei,
fara a include - totusi - acumularile minore, care
complica in mod inutil modelul matematic.
c). Ecuatia de bilant, cu acumulare variabila de masa sau energie, reprezinta o ecuatie de stare numai daca acumularea respectiva nu este consecinta nemijlocita a unui proces dinamic descris de o alta acumulare dintr-o ecuatie de bilant. De exemplu pentru circuitul unui lichid incalzit intr-un schimbator de caldura, ecuatia de bilant material conduce la o acumulare variabila de substanta, dar nu ca efect al compresibilitatii fluidului (lichidele se considera, de regula, incompresibile), ci datorita variatiei in timp a densitatii. Dinamica temperaturii fluidului incalzit, determinata de acumularea din ecuatia de bilant termic, produce - in mod univoc - o dinamica a densitatii lichidului, deci si o variatie a acumularii in ecuatia de bilant material, fara ca cele doua acumulari sa poata evolua independent. Intrucat acumularea din ecuatia de bilant energetic determina in mod univoc acumularea din ecuatia de bilant material, nu avem doua ecuatii diferentiale independente, ci una singura: cea corespunzatoare bilantului termic. Ecuatia de bilant material se numeste reductibila, in sensul ca - prin substituirea derivatei densitatii cu expresia data de ecuatia de bilant termic - ea se transforma intr-o ecuatie algebrica.
Daca insa fluidul incalzit in schimbatorul de caldura este un gaz compresibil, atunci acumularea de substanta din ecuatia de bilant material poate fi consecinta si a variatiei densitatii cu presiunea (gazele fiind compresibile). In acest caz, acumularile din ecuatiile de bilant material si energetic nu rezulta in mod univoc una din cealalta si fiecare ecuatie diferentiala de bilant reprezinta cate o ecuatie de stare in modelul matematic.
Rezulta deci ca ordinul modelului, adica dimensiunea vectorului de stare, este egal cu numarul de ecuatii de bilant nereductibile, din ansamblul celor ce contin acumulari variabile.
Explicitarea variabilelor intermediare care apar in ecuatiile de stare. In partea dreapta a ecuatiilor de stare apar si variabile care nu sunt de intrare sau de stare. Acestea se numesc variabile intermediarei. Ele trebuie explicitate in functie de marimile de intrare si de stare, utilizand relatii din domeniul corespunzator proceselor fizice din instalatie. Adesea, prin expresia unei variabile intermediare, se introduc noi variabile intermediare, care trebuie explicitate la randul lor.
Ordonarea ecuatiilor modelului matematic. Se face in asa fel, incat in partea dreapta a oricarei ecuatii din model sa intervina: variabile de intrare, variabile de stare, variabile intermediare care deja au fost definite printr-o relatie scrisa anterior.
Eliminarea, prin substitutii, a variabilelor intermediare si prezentarea modelului matematic prin doua categorii de ecuatii:
ecuatii de stare (diferentiale), care determina evolutia vectorului de stare, sub actiunea vectorului marimilor de intrare;
ecuatii de iesire (algebrice), prin care se exprima marimile de iesire in functie de marimile de stare si, eventual, de intrare. De regula, marimile de iesire sunt fie variabile de stare, fie variabile care au fost considerate - in fazele anterioare - ca variabile intermediare. Prin urmare, problema deducerii ecuatiilor de iesire se rezolva implicit, in cadrul operatiilor de stabilire a ecuatiilor de stare.
Procedura prezentata, pentru modelarea matematica a instalatiilor automatizate, se poate utiliza sub doua forme:
- considerand ecuatiile de bilant aplicate unor elemente spatiale finite, rezultand capacitati de acumulare finite si concentrate; in acest caz, modelul matematic se mai numeste si sistem cu parametri concentrati, fiind format din ecuatii diferentiale ordinare;
- aplicand ecuatiile de bilant unor elemente spatiale infinitezimale, rezultand capacitati de acumulare infinit mici si distribuite spatial; in acest caz, modelul matematic se mai numeste si sistem cu parametri distribuiti, avand in componenta si ecuatii cu derivate partiale.
|
Politica de confidentialitate |
| Copyright ©
2024 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |