
Proiectarea cristalelor fotonice
1 Tipuri de cristale fotonice
Sunt trei tipuri de cristale fotonice in functie de modul de proagare a fascico-lului de fotoni prin cristal: unudimensional, pentru care banda interzisa exista doar pentru o singura directie de propagare, bidimensional cu o banda fotonica interzisa in doua directii de propagare si tridimensional care prezinta o banda fotonica interzisa completa.
Analog structurii semiconductorilor in care banda de conductie si banda de valenta sunt despartite de banda interzisa, s - a hotarat ca banda de deasupra benzii fotonice interzise sa fie numita "banda de aer" si cea de sub ea "banda de dielectric Fotonii se decupleaza in modurile transversal magnetic (TM) si transversal electric (TE). In urma unor experimente s - a ajuns la concluzia ca benzile fotonice interzise pentru modurile TM sunt favorizate intr - o retea de regiuni cu un ε ridicat, izolate intre ele, iar benzile interzise pentru modurile TE se gasesc in retele conectate. Ceea ce este important de subliniat este ca periodicitatea cristalului a dus la aparitia unei benzi fotonice interzise.
Putem caracteriza suprafata unui cristal
fotonic in functie de inclinare si terminatie. Inclinarea se
refera la unghiurile dintre normala la suprafata si axele
cristalului, iar terminatia specifica unde se taie suprafata de
- a lungul celulei unitate. Modurile de suprafata apar cand in apropierea
cristalului sunt moduri electromagnetice care nu se pot propaga in cristal
datorita benzii interzise. Totodata aceste moduri depind si de
vectorul de unda k. Pentru a gasi aceste moduri, alegem (ωs,
k) si incercam sa gasim un vector de unda
perpendicular pe suprafata, k![]() pentru care ωs = ωn
(k, k
pentru care ωs = ωn
(k, k![]() ), unde ωn este o frecventa care se poate
propaga prin cristal. Acest procedeu de a gasi toti k
), unde ωn este o frecventa care se poate
propaga prin cristal. Acest procedeu de a gasi toti k![]() pentru fiecare k se numeste "proiectia
structurii de benzi pe suprafata zonei Brillouin
pentru fiecare k se numeste "proiectia
structurii de benzi pe suprafata zonei Brillouin
In figura 1.3 este schitat un cristal fotonic format dintr - o retea de bare dielectrice. Pentru cazul a) nu exista moduri de suprafata. Pentru un cristal ale carui bare dielectrice sunt taiate pe jumatate conform cazului b avem de - a face cu moduri de suprafata. Daca continuam sa indepartam aceste bare atunci banda dielectrica s - ar suprapune peste banda de aer. Astfel s - a ajuns la concluzia ca pentru un cristal fotonic cu o anumita inclinatie se poate gasi o anumita terminatie care sa permita existenta modurilor de suprafata. Modurile de suprafata sunt unde care decad exponential in cristalul fotonic, fara sa treaca de acesta. Dar se pot crea defecte ale cristalului astfel incat fluxul fotonic sa fie captat in cristal.
● ● ●
![]()
![]()
![]()
● ● ● ● ● ●
● ● ● ● ● ● cristal cristal
a) b)
Figura 1.3 Cristal fotonic 2D
De exemplu putem realiza o vacanta in reteaua de bare de dielectric ca in figura 2. Prin inlaturarea unei bare din retea obtinem o cavitate care e inconjurata de pereti reflectorizanti. Daca cavitatea are dimensiunea potrivita astfel incat sa ii corespunda un mod electromagnetic din banda interzisa, atunci nu poate iesi din cristal si ii putem asocia un mod defectului [13
Daca defectul presupune indepartarea de dielectric, "un defect de aer",modul corespunzator cavitatii trece din banda dielectrica in banda interzisa si in functie de cantitatea de dielectric indepartata poate ajunge in banda de aer. Analog daca defectul presupune adaugarea de material dielectric modul cavitatii coboara din banda de aer in banda interzisa. In ambele cazuri defectul poate fi obtinut oriunde in banda interzisa. Totodata folosind defecte in linie ghidam fascicolul de fotoni dintr - o zona in alta. In figura 3 este evidentiat un ghid de unda prin indepartarea unui rand vertical de bare. Acesta este un mecanism nou de ghidare a luminii, pana acum cea mai utilizata fiind fibra optica, care se bazeaza pe reflexia interna totala. Insa daca o fibra optica se curbeaza mai puternic unghiul de incidenta este prea mare ca sa mai aiba loc reflexia totala interna si fascicolul de fotoni iese pe la colturi. Cristalele fotonice continua sa ghideze fascicolul de fotoni chiar si pentru curbe foarte stranse, deoarece frecventa modului ghidat este in interiorul benzii interzise acesta nu se disipa in cristal fapt ilustrat de in figura 4. Chiar daca raza de curbura este mai mica decat lungimea de unda, aproape tot fascicolul de fotoni care intra pe la un capat iese prin celalat singurele pierderi sunt date de reflexia de la intrarea ghidului [15].
Multe din aplicatiile cristalelor fotonice, care includ lasere si rezonatori cu pierderi foarte mici, necesita folosirea materialelor fotonice cu benzi complete. Prima structura care prezinta o banda interzisa 3D este structura de diamant, lucru evidentiat de Ho Chan si Soukoulis in urma calculelor teoretice a propagarii undelor electromagnetice in medii dielectrice periodice, iar primul material fotonic realizat de Yablonovitch avea simetrie fcc.


Figura 2.3 Defect punctual, cristal 2D Figura 3 Defect in lungime, cristal 2D
Cercetatorii de la MIT au demonstrat ca structura de diamant ofera o banda completa de - a lungul intregii suprafete a zonei Brillouin [16].

Figura 4.3 Ghidajul fascicolului de fotoni printr - un un cristal 2D
Si alte grupuri de cercetare au demonstrat teoretic existenta unei benzi fotonice interzise in structura de diamant. Calculele teoretice s - au bazat pe natura vectoriala a campului electromagnetic, in timp ce daca s- ar face calcule scalare nu am obtine rezultate corecte. Banda fotonica interzisa apare daca avem un raport al indicilor de refractie mai mare decat 2 si o gama larga de raporturi de umplere pentru o retea de sfere intr - o structura de diamant.
Elementele
de baza necesare pentru a obtine o banda fotonica
interzisa sunt conectivitatea(geometria
materialului), contrastul dielectric si raportul de umplere. Rezulta de aici intrebarea: Cu ce tipuri de structuri se pot obtine benzi
fotonice interzise
Pentru a raspunde la aceasta intrebare se definste ![]() care este
frecventa din mijlocului benzii interzise,
care este
frecventa din mijlocului benzii interzise, ![]() unde
unde ![]() este viteza efectiva a undelor electromagnetice in
mediu, iar
este viteza efectiva a undelor electromagnetice in
mediu, iar ![]() este vectorul de unda corespunzator lui
este vectorul de unda corespunzator lui![]() si care este proportional cu inversul constantei de
retea. Daca o anumita structura are sau nu o banda
interzisa depinde de suprapunerea dintre frecventei cele mai mici din
banda de valenta si frecventei cele mai mari din banda de
conductie de - a lungul
suprafetei zonei Brillouin. Pentru structura de diamant, atat cel mai mic
vector de unda (L)
la suprafata zonei Brillouin cat si celui mai
mare vector de unda (W sau K) determina inceputul benzii de conductie. Geometria
diamantului sau a structurii fata centrata tetragonala
(fct) este de asa natura ca cele doua frecvente de
banda nu se suprapun. In cele mai multe structuri cele doua
frecvente la cele doua puncte L si W coincid si atunci nu
am mai avea o banda fotonica interzisa.
si care este proportional cu inversul constantei de
retea. Daca o anumita structura are sau nu o banda
interzisa depinde de suprapunerea dintre frecventei cele mai mici din
banda de valenta si frecventei cele mai mari din banda de
conductie de - a lungul
suprafetei zonei Brillouin. Pentru structura de diamant, atat cel mai mic
vector de unda (L)
la suprafata zonei Brillouin cat si celui mai
mare vector de unda (W sau K) determina inceputul benzii de conductie. Geometria
diamantului sau a structurii fata centrata tetragonala
(fct) este de asa natura ca cele doua frecvente de
banda nu se suprapun. In cele mai multe structuri cele doua
frecvente la cele doua puncte L si W coincid si atunci nu
am mai avea o banda fotonica interzisa.
Din punct de vedere experimental, Yablonovitch a
demonstrat existenta materialelor cu banda fotoonica
interzisa. Cristalul de Yablonovite are simetria structurii de diamant cu
un raport de umplere de 85%, iar raportul teoretic banda interzisa mijlocul
benzii interzise este de 19%. Daca avem o structura cu simetrie de
diamant cu sfere de aer in interior am obtine un raport banda
interzisa mijlocul
benzii interzise de 29%. Structura fata centrata cubica
(fcc) nu are o banda interzisa completa intre benzile 2 si
3 [2]. (vezi Tabelul 1) Calculele teoretice pentru sfere de aer intr - o retea
fcc au evidentiat o suprapunere a benzilor 3 si 2 pentru unde p - polarizate de - a lungul
suprafetei zonei Brillouin intre U si X. Aceste benzi sunt degenerate
la punctul W. Aceste proprietati au condus la aparitia unei
regiuni de stari cu densitati scazute numita si "pseudobanda
interzisa". S - a incercat proiectarea unor structuri
cristaline 3D care sa fie usor fabricate experimental. Astfel, s - a
construit un material fotonic pornind de la un material gazda cu simetrie
de diamant in interiorul caruia s - au introdus cilindrii de dielectric.aceasta
structura avea benzi intrzise de aproape 30% pentru bare de dielectric sau
de 28% pentru bare de aer. S - a incercat
reducerea dimensiunilor blocurilor care formeaza materialul. Astfel un
grup de cercetatori din S.U.A au proiectat o noua structura 3D
numita strat
peste strat"si prezentata in figura 4.4. Acest material consta din straturi de
bare unudimensionale, cu o asezare care se repeta la fiecare 4
straturi, iar distanta din 4 in 4 straturi este c. In interiorul
fiecarui strat barele sunt aranjate astfel incat sa fie paralele
intre ele, cu distanta a intre
doua bare. Barele din stratul urmator sunt rotite cu unghi ce
variaza intre 90° si 60°. Barele din din stratul al trei - lea sunt mutate cu jumatate distanta
dintre bare, in raport cu barele din primul strat. Barele din fiecare strat
alternant sunt paralele. Aceasta structura are o simetrie
fata centrata tetragonal. Pentru cazul in care c a = ![]() reteaua
poate fi obtinuta dintr - o celula unitate fcc.
reteaua
poate fi obtinuta dintr - o celula unitate fcc.
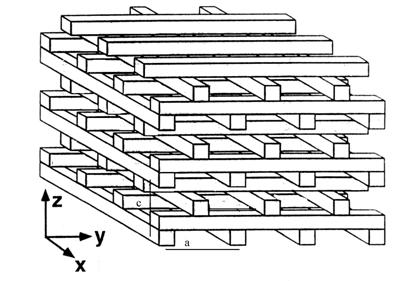
Figura 5.3 Structura strat peste strat
Structura strat peste
strat" permite modificarea unei game largi de parametrii dimensionali. Barele
pot avea o forma dreptunghiulara, circulara, eliptica cu
diferite raporturi de umplere. Materialul gazda poate fi un dielectric cu
indice de refractie mare sau poate fi aer. Alternativ structura poate fi construita
din bare de aer intr - un bloc de material dielectric. O proprietate
importanta a acestei structuri este dualitatea,
adica de exemplu un material poate fi descris ca e format din
bare de aer care se ating de grosime ![]() sau ca e format
din bare de dielectric de grosime
sau ca e format
din bare de dielectric de grosime ![]() printre care
circula aer. Acest caracter dual este folositor pentru calcule. Nu este
necesar ca barele sa se atinga ca in figura 5.3, se pot doar
suprapune. De fapt, acesta geometrie a structurii, astfel incat barele sa
nu se atinga, produce benzi fotonice mai largi. S - a optimizat banda fotonica interzisa
in functie de parametrii structurali. Acestia sunt
printre care
circula aer. Acest caracter dual este folositor pentru calcule. Nu este
necesar ca barele sa se atinga ca in figura 5.3, se pot doar
suprapune. De fapt, acesta geometrie a structurii, astfel incat barele sa
nu se atinga, produce benzi fotonice mai largi. S - a optimizat banda fotonica interzisa
in functie de parametrii structurali. Acestia sunt
raportul c/a,
raportul de umplere a structurii care e controlat prin variatia largimii barelor,
contrastul dielectric dintre cele doua materiale,
gradul de suprapunere dintre barele de dielectric.
Primul cristal fotonic "strat peste strat" care a fost fabricat functioneaza in domeniul microundelor, are o banda fotonica interzisa completa intre 12 si 14 GHz si este alcatuit din bare cilindrice de aluminiu. O structura similara a fost realizata din bare dreptunghiulare de aluminiu si are o banda interzisa intre 18 si 24 GHz. In cazul materialelor fotonice realizate din bare cilindrice care se ating ca in figura 5.3 cu raza unui cilindru r, iar distanta centru - la - centru dintre cilindrii a, raportul de umplere este de f = πr/2a. Raza controleaza si raportul c/a deoarece c = 8r. S - au calculat benzile fotonice in functie de raportul de umplere f = 0,22 iar c a = 1,27 si s - a determinat ca pentru o structura 3D "strat peste strat" formata din cilindrii de dielectric suprapusi, cu un raport al indicilor de refractie n = 3,6 raportul optim banda interzisa mijlocul benzii interzise este de 18%. Daca se folosesc cilindrii de forma eliptica banda interzisa este aproape inexistenta. Este important faptul ca pentru structura inversa cu cilindrii de aer intr - un material dielectric rezulta o banda interzisa mult mai mare de aproape 25%, iar pentru bare de aer de forma eliptica de 27%. Aceste structuri cu 80 - 85% aer cu o geometrie multiplu-conectata au benzi fotonice mai largi, iar pentru conceperea lor s- a utilizat corodarea ionica.
Tabelul 1. Materiale fotonice cu diferite simetrii de retea.
|
Simetrie |
Element |
Materialul elementului |
Benzi |
Banda inter-zisa/mijlocul benzii interzise |
|
fcc |
sfere |
aer |
pseudobanda |
|
|
fcc |
sfere |
aer | ||
|
diamant |
sfere |
sfere dielectrice | ||
|
diamant |
sfere |
sfere de aer | ||
|
diamant |
3 cilindrii |
cilindrii de aer | ||
|
fct 4 straturi |
bare dreptunghiulare |
nesuprapunere aer dielectric | ||
|
fct 4 straturi |
suprapunere |
bare de aer | ||
|
fct 4 straturi |
cilindrii care se ating |
dielectric | ||
|
fct 4 straturi |
cilindrii+sfere |
dielectric | ||
|
fct 4 straturi |
cilindrii |
aer - circular | ||
|
fct 4 straturi |
cilindrii |
aer - elliptic | ||
|
diamant |
3+1 cilindrii |
aer | ||
|
diamant |
3+1 cilindrii |
dielectric | ||
|
rombica |
cilindrii |
aer | ||
|
rombica |
cilindrii |
dielectric |
Pentru modelul experimental din domeniul microundelor din cilindrii de aluminiu care se ating cu un raport de aspect c/a = 1,13 iar raportul de umplere de 0,22 este necesar. un contrast al indicilor de refractie de minimum 2,2 pentru a obtine o banda fotonica interzisa, iar pentru n = 5,2 rezulta un raport banda interzisa mijlocul benzii interzise de 30%. Pentru a vedea cum se modifica banda interzisa, s - au introdus sfere din acelasi material dielectric ca si cilindrii la intersectia straturilor pentru a le uni. S -a determinat ca daca sferele au un volum mai mare de 10% din volumul cilindrilor, atunci banda interzisa devine mai larga datorita cresterii raportului de umplere si a geometriei rezultate. S - au calculat benzile fotonice de - a lungul directiei [110] si corespund cu rezultatele experimentale. Maximul benzii de valenta este in punctul K (0,75 0,75 0) la 11,7 GHz, iar experimental la 11,9 GHz pentru unde electromagnetice polarizate perpendicular pe cilindrii, intervalul de frecvente al benzii interzise avind o valoare limita superioara de 13,7 GHz calculata si 14 GHz experimentala. Banda interzisa este mult mai larga pentru propagarea undelor perpendicular pe straturi, in directia de asezare a acestora, limitele in punctul X fiind de 11,1 si 16,8 GHz fata de 10,7 si 17,4 GHz. (vezi Tabelul 2) Minimul benzii de conductie se situeaza in punctul L (0,5 0,5 0,5).
In cazul in care avem o structura cu bare dreptunghiulare de aer intr - un material dielectric astfel incat sa nu se suprapuna unele peste altele rezulta un raport banda interzisa mijlocul benzii interzise de 18% pentru un cristal cu 70% aer. Cand barele de aer se ating banda interzisa creste la 22%, similar structurilor cilindrice cu o geometrie multiplu-conectata. Trebuie observat ca barele dreptunghiulare care se suparapun nu conduc la o banda fotonica interzisa cu aceleasi dimensiuni ca un sistem cilindric.
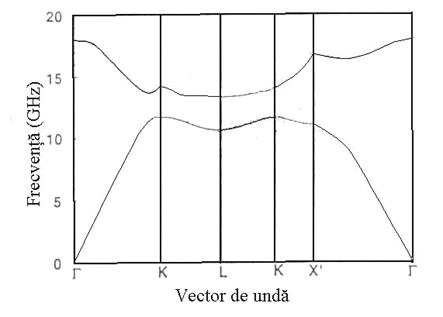
Figura 6.3 Frecventa in functie de vectorul de unda de - a lungul directiei [110] a zonei Brillouin. Calculele s - au facut astfel incat intensitatea campului electric sa fie perpendiculara pe bare.
Au fost fabricate structuri "strat peste strat" din bare dreptunghiulare de siliciu prin corodarea anizotropica a plachetelor in directia [110]. Au fost calculate benzile fotonice interzise pentru diferite valori ale raportului de aspect si s - a ajuns la concluzia ca pentru c/a intre 1,2 si 1,6, iar raportul de umplere intre 0,25 si 0,30 obtinem banda interzisa/mijlocul benzii interzise de aproape 20%. In aceste calcule c/a este mentinut constant in timp ce latimea barelor variaza. Daca crestem raportul de
umplere, atunci largimea benzii fotonice interzise scade. Minimul benzii de conductie este in punctul L, iar maximul benzii de valenta este aproape de K. Structura cu bare dreptunghiulare de siliciu a fost fabricata la trei lungimi de scala cu frecvente centrale din banda interzisa de 98,5, 325 si 439 GHz. S - a realizat o crestere a frecventei din mijlocul benzii interzise de la 20,1 GHz la 439 GHz.
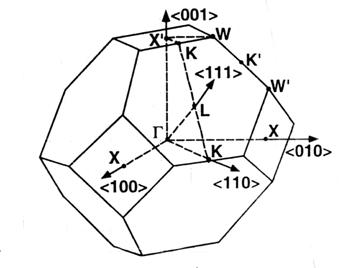
Figura 7.3 Prima zona Brillouin a unui cristal fotonic cu simetrie fcc
Tabelul 2. Intervalul de frecvente corespunzator propagarii undelor de - a lungul directiei de asezare a straturilor.
|
Ma-terial |
Index de refrac-tie |
Frecventa centrala masurata [GHz] |
Frecventa inferioara masurata [GHz] |
Frecventa inferioara calculata [GHz] |
Frecventa superioara masurata [GHz] |
Frecventa superioara calculata [GHz] |
|
Al. | ||||||
|
Al. | ||||||
|
Si. | ||||||
|
Si. | ||||||
|
Si. |
S - a incercat o variatie a structurii "strat peste strat", astfel incat barele dreptunghiulare de siliciu din stratul urmator s - au rotit cu un unghi θ = 70s5 fata de cele din stratul anterior anterior. Daca se reduce θ de la 90s la 70s5 atunci si banda fotonica interzisa se reduce cu 12%.
O clasa interesanta de structuri sunt cele cu simetrie rombica, A - 7, iar materialul fotonic se realizeaza conectand puncte din retea cu cilindrii. Astfel avem benzi interzise de aproape 30%.
O structura alternativa strat peste strat" a fost propusa de San Fan. Ea consta din doua materiale dielectrice asezate unele peste altele in care s - au facut gauri de aer. Parametrii dimensionali au fost optimizati astfel incat sa rezulte rapoarte banda interzisa/mijlocul benzii interzise de 14% folosind Si, SiO2 si aer si de 23% utilizand Si si aer.
In concluzie banda fotonica interzisa depinde in mod crucial de conectivitate si geometrie, contrastul indicilor de refractie si de raportul de umplere al structurii. S - a proiectat o noua structura strat peste strat" care prezinta o banda fotonica interzisa completa. Fiecare strat e alcatuit din bare paralele intre ele, iar barele din stratul urmator sunt rotite cu 90s. Aceasta metoda de asezare a dus la formarea unei celule unitate de 4 straturi. Exista diferite moduri de clasificare a cristalelor fotonice in functie de materialele folosite semiconductori, metale in functie de forma barelor cilindrice, dreptunghiulare, eliptice si in functie de simetria materialelor: diamant, fata centrata cubica, rombica. Am prezentat aceste structuri 3D pentru a evidentia aceasta varietate. S - au realizat structuri din aluminiu si siliciu din bare cilindrice, dreptunghiulare ca si structuri inverse. Frecventele centrale din banda fotonica interzisa sunt in intervalul 12,6 si 439 GHz.. Aceste materiale strat peste strat" prezinta un interes deosebit deoarece pot fi scalate dimensional astfel incat sa functioneze in domeniul de frecvente infrarosu, ceea ce ar conduce la noi aplicatii pentru cristalele fotonice.
In subcapitolele urmatoare voi prezenta cateva din aplicatiile cristalelor fotonice cum ar fi: ghiduri de unda 1D, microcavitati in ghiduri canal, fibra din material fotonic 2D, utilizarile cristalelor 3D in microunde.
2 Materiale fotonice 1D
2.1 Ghid de unda
Dintre varietatea de utilizari a cristalelor fotonice, realizarea ghidurilor de unda folosind materiale fotonice 1D, prezinta un interes deosebit deoarece coeficientul de transmisie se apropie de 90%. Trebuie mentionat faptul ca spre deosebire de laserele DFB a caror structura reticulara prezinta un contrast al indicilor de refractie de cel mult 1%, structurile fotonice cu banda interzisa necesita un contrast al indicilor de refractie mai mare de 2 1 [19]. Prima problema care rezulta din studierea acestor retele cu un raport al indicilor de refractie ridicat se refera la dimensiunea fizica a ghidului de unda, cat de multe grilaje trebuie puse astfel incat sa avem o banda fotonica interzisa. S - a determinat ca pentru o structura din GaAs cu o perioada de 400 nm urmata de zone cu aer largi de 80 nm, banda fotonica interzisa in intervalul lungimilor de unda 800 - 900 nm incepe sa se formeze pentru doua perioade. Banda interzisa este aproape formata pentru 4 perioade si este definitivata pentru 6 perioade. In comparatie cu structurile BFI ideale care au o atenuare de 16 dB/celula unitate, aceasta retea are o atenuare de 3 dB/celula unitate. Motivul acestei atenuari scazute este acela ca drumul optic nu este λ/4. Interactiile sunt suficient de puternice astfel incat sa se formeze o banda fotonica interzisa pentru un ghid de unda lung de cativa microni [13].
S - a mai studiat un alt tip de ghid de unda, un ghid de unda pentru un singur mod, cu o grosime de 0,2 μm si cu o diferenta a indicilor de refractie de 0,2(3,5 - 3,3). Aceste tipuri de ghiduri de unda sunt folosite pentru lasere cu semiconductori. Ghidul de unda este realizat din GaAs, pe un substrat de AlGaAs. Stratul pentru ghidaj, este pozitionat deasupra structurii pentru a minimiza adancimea corodarii. Pentru ca structura sa poata fi fabricata s - a ales o adancime de corodare de 0,8 μm iar distanta dintre gratii de 100 nm. Perioada este de 425 nm. Dupa trecerea prin 5 zone de aer, transmisia ghidul de unda a scazut la 65%, neluand in calcul si pierderile datorate reflexiilor. Acest rezultat poate fi inbunatatit la 82% mentinand aceiasi parametrii mai putin grosimea ghidului care a crescut de la 0,2 μm la 0,4 μm. Rezultatul nu se modifica chiar daca se mareste contrastul indicilor de refractie. Daca se reduce adancimea de corodare de la 0,8 μm la 0,5 μm pierderile sunt mai mari, transmisia scazand la 43%, ceea ce inseamna ca zonele cu aer trebuie sa fie cat mai adanci posibil. Modificand un alt parametru, latimea zonelor cu aer la 50 nm pierderile s - au redus cu inca 10%, de unde rezulta ca transmisia ghidului de unda a crescut la 92%. Banda interzisa este intre 820 si 900 nm. Calculele teoretice s - au efectuat folosind metoda matricei de transfer. Structura prezentata in acest paragraf a fost fabricata, iar masurarile experimentale au fost facute utilizand un laser Ti : Safir a carui gama de acord este intre 820 si 930 nm. Fluxul de fotoni se propaga aproximativ 500 μm, interactionaza cu ghidul de unda si se mai propaga inca 500 μm inainte sa ajunga la un detector. Banda fotonica interzisa obtinuta experimental este intre 840 si 910 nm.
In cazul unei astfel de structuri semiconductor - aer totdeauna vor exista anumite pierderi. Acestea sunt datorate faptului ca fluxul fotonic este ghidat numai de regiunea semiconductoare, iar in zonele cu aer au loc difractii si nu mai este o confinare a modului. Pierderile prin difractie pot fi eliminate daca in locul aerului se foloseste un dielectric astfel incat sa se realizeze o suprapunere perfecta intre modul ghidat atat in regiunile cu un indice de refractie mare cat si in cele cu un indice de refractie mic.
Mai sunt si alte tipuri de ghiduri de unda, nu numai in forma de structura reticulara cu un raport al indicilor de refractie mai mare de 2, de exemplu ghidul din figura 8.
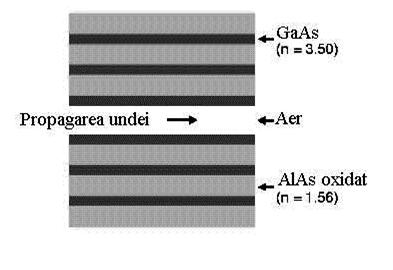
Figura 8.3 Ghid de unda dintr - un cristal 1D
Ghidul de unda din figura de mai sus este alcatuit din mai multe straturi de GaAs (n 3,5) si de AlAs oxidat (n 1,56), grosimea stratului de AlAs fiind dubla fata de grosimea stratului de GaAs. S - a inlaturat un strat de AlAs oxidat astfel incat propagarea undei sa se faca de - a lungul unei zone cu aer inconjurata de materialul cu un indice de refractie mai ridicat. Pierderile sunt foate mici, coeficientul de trnasmisie pentru modul fundamental fiind de 98,8%.

Figura 9.3 Ghid de unda dintr - un cristal 1D cu un cristal 2D
O alta structura care ghideaza fascicolul de fotoni este prezentata in figura 9. Ea este formata din doua cristale fotonice 1D ca cele de mai sus care acum au rolul de pereti reflectorizanti si un material fotonic 2D care reprezinta de fapt ghidul de unda. Astfel se poate realiza un ghid de unda hibrid asemenea unui cristal fotonic 3D dar mult mai simplu de fabricat. Acest nou tip de ghid de unda poate transporta fascicolul de fotoni prin curbe extrem de stranse dar cu pierderi foarte mici, sugerand posibilitatea realizarii de circuite fotonice integrate cu o densitate de integrare foarte mare.
2.2 Microcavitati in ghiduri de unda canal
Microcavitati la frecvente din domeniul microundelor pot fi fabricate utilizand pereti metalici puternic reflectorizanti, dar pentru frecvente optice metalele au pierderi foarte mari si de aceea trebuie folosite alt tip de materiale. Cristalele fotonice pot fi utilizate pentru realizarea de microcavitati deoarece elimina pierderile de radiatie in orice directie.
In acest subcapitol voi prezenta o noua clasa de microcavitati coplanare care utilizeaza un ghid de unda canal pentru a confina fluxul fotonic in doua dimensiuni si un cristal fotonic 1D pentru a confina fotonii in cea de - a trei - a. Conceptual aceaste microcavitati sunt asemanatoare cu rezonatoarele Fabry - Perot diferenta constand in faptul ca au o geometrie coplanara si o confinare foarte puternica a campurilor. Totodata aceste microcavitati pot fi fabricate folosind tehnici litografice conventionale aplicate materialelor semiconductoare.
Pentru a proiecta o microcavitate trebuie sa raspundem la doua intrebari care sunt modurile din cavitate si cum putem cupla enegia cu aceste moduri Pentru a raspunde la aceste intrebari folosim doua metode de calcul computerizate. Cele doua metode sunt din domeniul timp si domeniul frecventa si au fost prezentate in capitolul 2. Prima metoda ne permite sa determinam comportamentul temporal al microcavitatii eficienta la cuplaj, pierderile prin imprastiere, factorul de calitate, iar cu cea de - a doua rezulta starile proprii si distributia modurilor
Microcavitatile sunt realizate din ghiduri de unda canal cu un indice de refractie ridicat. Variatia periodica a indicelui de refractie se face prin corodarea unor gauri verticale in ghid, iar microcavitatea se formeaza prin adaugarea de material dielectric intre doua gauri. Pentru a intelege mecanismul confinarii campurilor in microcavitate, este folositor sa investigam mai intai care este efectul gaurilor asupra proprietatilor modurilor ghidate.
Modurile din ghidul de unda sunt determinate cu metoda domeniu frecventa pentru care se face aproximarea supercelulei, ghidul cu tot cu gaurile verticale este plasat intr - o supercelula care este repetata periodic in spatiu. In figura 11.3 este ilustrata relatia de dispersie pentru ghidul de unda canal cu gauri verticale, pentru modurile cu simetrie para fata de planul (x,y). Ghidul de unda dielectric este realizat din GaAs cu un indice de refractie de 3,37 la 1,55 μm. Relatia de dispersie s - a obtinut prin determinarea starilor proprii cu frecventele cele mai scazute a ghidului de unda in functie de valorile vectorului de unda de - a lungul directiei de propagare. Ghidul de unda, prezentat in figura 10.3, are o lungime de 1,2a si o inaltime de 0,4a, unde a este constanta de retea a dielectricului si in acelasi timp si distanta de la un centru la celalat dintre doua gauri vecine. Gaurile au un diametru de 0,6a. Constanta dielectricului ghidului este de 11,36. Acesti parametrii structurali au fost alesi astfel incat sa obtinem o buna confinare a intensitatii campului electric in microcavitate.
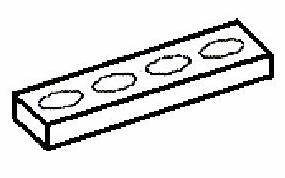
Figura 10.3 Ghid de unda dielectric
Graficul din figura 11.3 reprezinta relatia de dispersie pentru prima zona Brillouin. Starile de deasupra liniei diagonale nu sunt ghidate prin dielectric. Diagonala reprezinta marginea conului de lumina. Starile de sub diagonala sunt evanescente de - a lungul axelor x si z si sunt ghidate prin dielectric. Intre primul si cel de al doi - lea mod ghidat apare o banda interzisa. Aceasta banda interzisa nu se intinde peste toata zona Brillouin, ea exista doar pentru modurile ghidate. Banda fotonica interzisa joaca un rol foarte important, permitand unui mod sau grup de moduri sa se propage daca se face un defect in structura periodica. Dimensiunea benzii interzise este determinata de constanta dielelctricului ghidului de unda si de raza gaurilor verticale. In cazul nostru raportul banda interzisa mijlocul benzii interzise este de 27%.
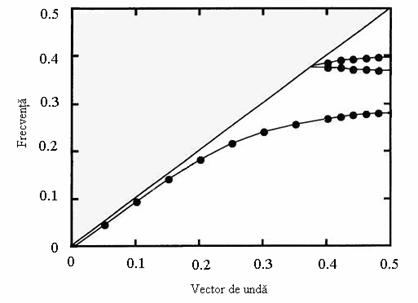
Figura 11.3 Graficul relatiei de dispersie pentru modurile din
ghidul de unda canal
Pentru a observa natura benzii interzise vom examina intensitatea campului electric pentru primele doua benzi. In figura 12.3 este prezentat vectorul intensitatea campului electric in planul (x, y) trecand prin mijlocul ghidului, in functie de un vector de unda la marginea zonei Brillouin. Campul este confinat de - a lungul ghidului de unda si decade exponetial daca ne indepartam de el, caracteristica specifica modurilor ghidate. In cazul figurii 12.3 a) intensitatea campului electric este concentrata puternic in regiunile cu dielectric din jurul fiecarei gauri cu aer, spre deosebire de figura 12.3 b) unde intensitatea campului electric este concentrata in interiorul gaurilor cu aer.

Figura 12.3 Vectorul intensitatea campului electric asociat a) cu prima si b) a doua banda interzisa
Acum vom
introduce un defect in structura ghidului de unda. Acest defect
consta in adaugarea de material dielectric intre doua
gauri. Initial aceasta stare este deasupra benzii interzise, iar
cu cat adaugam mai mul dielectric patrunde si mai mult in
interiorul benzii interzise. Astfel rezulta moduri rezonante care este confinat
in apropierea defectului. Acest mod rezonant isi cupleaza energia cu
modul ghidului de unda prin campuri evanescente de - a lungul grupului de
gauri. In figura 13 este ilustrat modul rezonant al unei
cavitati care contine 6 gauri verticale cu aer, cu 3
gauri de - o parte si de alta a defectului. Frecventa acestui
mod este de 0,31![]() a
unde
a
unde ![]() este viteza luminii in
vid, iar a este constanta de retea. Cum ne asteptam frecventa
este in interiorul benzii interzise, dupa cum vedem si in figura 11.
Gaurile actioneaza ca oglinzi Bragg.
este viteza luminii in
vid, iar a este constanta de retea. Cum ne asteptam frecventa
este in interiorul benzii interzise, dupa cum vedem si in figura 11.
Gaurile actioneaza ca oglinzi Bragg.
Daca marim numarul de gauri atunci are loc o confinare si mai buna a campului in cavitate. Insa aceasta idee are si un neajuns in sensul ca se reduce abilitatea de cuplaj a fluxului de fotoni in afara si in interiorul cavitatii. Un compromis ar fi micsorarea numarului de gauri numai pe o parte a cavitatii.
Modificand diferiti parametrii ai cavitatii putem ajusta numarul de moduri rezonante in banda interzisa, frecventa lor si gradul de confinare in cavitate. Acesti parametrii sunt inaltimea si lungimea ghidului de unda, raza gaurilor, distanta dintre doua gauri vecine si dimensiunea defectului.

Figura 13 Vectorul intensitatea campului electric asociat cu un defect in ghidul de unda
Deoarece microcavitatea poate functiona pentru orice
lungime de unda doar prin scalarea fiecarui parametru, este
convenabil sa alegem un parametru si sa - i scalam pe
ceilalti in raport cu el. Am ales drept parametru constanta de retea
a. In figura 13 defectul are dimensiunile d = 1,5a unde d este diatanta de
la un centru la celalat dintre gaurile de o parte si de alta a
defectului. Efectul acestui defect a fost sa introduca o singura
stare rezonanta in banda interzisa. Introducerea acestui defect poate
determina ca mai multe stari sa coboare din benzile de deasupra si
astfel mai multe stari vor aparea in banda interzisa. Modul din
figura 13 este modul rezonant fundamental. Primul mod rezonant de ordinul al
doi - lea apare la frecventa 0,37 ![]() a
care ii corespunde celei de a doua benzi din afara benzii interzise. Modurile
induse de defect si modurile ghidate din cea de a - doua banda nu se
cupleaza unele cu altele deoarece nu au aceeasi simetrie. Modurile
rezonante raman confinate in jurul defectului. Deoarece intre modul
rezonant fundamental si modurile rezonante de ordin mai mare exista
un interval destul de larg, aceste microcavitati pot avea la
iesire un singur mod.
a
care ii corespunde celei de a doua benzi din afara benzii interzise. Modurile
induse de defect si modurile ghidate din cea de a - doua banda nu se
cupleaza unele cu altele deoarece nu au aceeasi simetrie. Modurile
rezonante raman confinate in jurul defectului. Deoarece intre modul
rezonant fundamental si modurile rezonante de ordin mai mare exista
un interval destul de larg, aceste microcavitati pot avea la
iesire un singur mod.
Sunt doua posibilitati de realizare a unui defect adaugare sau indepartare de dielectric. Daca indepartam dielectric atunci modurile ghidate din prima banda trec in banda interzisa, iar rezultatele obtinute sunt asemanatoare cu celalat caz pe care l - am studiat, in sensul ca avem o buna confinare a intensitatii campului electric in jurul defectului si la iesire putem avea tot un singur mod.
Acum determinam comportamentul dinamic al modurilor in microcavitate eficienta la cuplaj dintre dintre modurile ghidate si modul rezonant din cavitate, influenta gaurilor asupra modurilor ghidate si factorul de calitate al cavitatii.
Pentru a avea o eficienta mare la cuplaj
trebuie ca modul din ghidul de unda sa aiba o componenta cu
aceeasi simetrie ca a modului rezonant. Modurile TE sunt acele moduri
pentru care intensitatea campul electric e polarizata paralel cu ghidul de
unda si este perpendiculara pe directia de propagare si
de aceea aceste moduri vor cupla energia mai eficient cu modul
cavitatii. Daca propagam un impuls gaussian prin ghidul de
unda, centrat pe frecventa 0,30![]() a
atunci apare un interval larg de frecvente intre 0,28
a
atunci apare un interval larg de frecvente intre 0,28![]() a
si 0,37
a
si 0,37![]() a
pentru care nu se transmite nimic, ceea ce corespunde cu rezultatele din figura
11. Modurile din banda interzisa sunt atenuate puternic si nu pot trece
de gaurile de aer, fiind reflectate inapoi. Pe de alta parte,
modurile din afara benzii interzise sunt transmise, pentru anumite
frecvente coeficien-tul de transmisie fiind de aproape suta la
suta. Modurile raman ghidate si prin gaurile de aer pierderile
prin imprastiere si reflexie fiind foarte mici. Daca
creeam cavitatea, atunci la frecventa 0,30
a
pentru care nu se transmite nimic, ceea ce corespunde cu rezultatele din figura
11. Modurile din banda interzisa sunt atenuate puternic si nu pot trece
de gaurile de aer, fiind reflectate inapoi. Pe de alta parte,
modurile din afara benzii interzise sunt transmise, pentru anumite
frecvente coeficien-tul de transmisie fiind de aproape suta la
suta. Modurile raman ghidate si prin gaurile de aer pierderile
prin imprastiere si reflexie fiind foarte mici. Daca
creeam cavitatea, atunci la frecventa 0,30![]() a apare
un varf de transmisie corespunzator modului rezonant. Eficienta la
cuplaj dintre modul ghidului de unda si modul rezonant depasind
80%.
a apare
un varf de transmisie corespunzator modului rezonant. Eficienta la
cuplaj dintre modul ghidului de unda si modul rezonant depasind
80%.
Factorul
de calitate Q masoara pierderile din cavitate. El are urmatoarea
definitie ![]() (1)
(1)
unde E'
este energia inmagazinata, ![]() este frecventa rezonanta,
iar P este puterea disipata.
este frecventa rezonanta,
iar P este puterea disipata.
Pentru a masura factorul de calitate pompam energie in cavitate si vedem cum scade in timp.

Figura 14.3 Factorul de calitate in functie de numarul de gauri de o parte si de alta a defectului
In figura 14.3 este prezentat factorul de calitate in functie de numarul de gauri de o parte si de alta a defectului. Pentru cavitatea noastra, care are 3 gauri de o parte si de alta a defectului, Q = 271. Daca numarul de gauri este mai mare atunci Q creste, iar pierderile scad. Insa Q nu poate sa creasca la infinit, iar daca sunt facute prea multe gauri atunci vor avea loc pierderi de energie. Astfel Q se satureaza, iar in cazul nostru valoarea maxima a lui Q este in jur de 700. Pentru ca eficienta cuplajului dintre modul ghidului si modul rezonant sa fie foarte buna, trebuie ca Q sa nu se satureze. Daca Q este maxim atunci toata energia cuplata cu cavitatea va radia in directii transversale.
Pentru a avea o buna confinare a radiatiei in microcavitate este necesar ca, contrastul dintre indicele de refractie al cavitatii si mediul inconjurator sa fie cat mai mare. Exista doua posibilitati prima care presupune suspendarea microcavitatii in aer, iar pentru cea de a doua, cavitatea este realizata pe un substrat cu un indice de refractie mic.
In primul caz microcavitatea este inconjurata de aer, ceea ce permite o buna confinare a intensitatii campului electric. Aceasta structura, prezentata in figura 15.3, se poate fabrica daca ghidul de unda se creste pe un substrat, iar apoi se indeparteaza o parte din substrat de sub cavitate. Doua gauri ale structurii sunt suspendate, iar celelalte sunt pe substrat. Daca corodam al - trei - lea set de gauri mai adanc astfel incat sa ajunga si in substrat, atunci optimizam si imprastierea modurilor de sub ghidul de unda. Microcavitatea este realizata din GaAs care are un indice de refractie de 3,37 la 1,55 μm, iar substratul din Al0,3Ga0,7As cu un indice de refractie de 3,07 la 1,55 μm. Acest contrast al indicilor de refractie este prea mic pentru ca ghidul de unda sa fi fost crescut direct pe substrat, pierderile unei structuri de acest tip fiind considerabile. Procesul de fabricatie este foarte simplu se depune un strat de AlAs de grosime 1 μm si peste el inca un strat de GaAs de 0,5 μm pe un substrat de GaAs. Structura ghidului si gaurile verticale au fost realizate prin corodare ionica reactiva. Stratul epitaxial de AlAs a fost indepartat prin corodare chimica. S - au fabricat microcavitati cu urmatoarele dimensiuni ghidul de unda are o lungime de 20 μm si o latime de 5,5 μm. Gaurile au un diametru de 2,5 μm cu o distanta de la un centru la celalat dintre doua gauri vecine de 5 μm.
Acest tip de microcavitati pot fi realizate si cu alte materiale semiconductoare nu numai cu materiale di grupele III - V. S - a fabricat o structura pe baza de siliciu dupa urmatorul proces tehnologic un strat de SiO2 gros de 1 μm s - a depus prin depunere chimica in stare de vapori la temperatura joasa. Peste el s - a depus un strat de Si de grosime 0,5 μm prin depunere chimica in stare de vapori la presiune scazuta. Ghidul de unda s - a facut prin corodare ionica reactiva a stratului de Si prin fotolitografie. Apoi s - a corodat SiO2. "Podul" din Si are 10 μm lungime si 4 μm latime. Patru gauri au fost plasate periodic de - a lungul ghidului de Si cu un diametru de 2 μm si cu o distanta de la centru la centru de 3 μm.
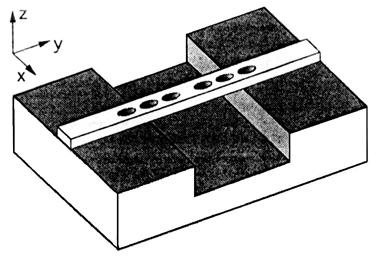
Figura 15.3 Microcavitate coplanara suspendata
Acest tip de microcavitati pot avea o alta geometrie, se pot creste direct pe un substrat cu un indice de refractie mic. Trebuie tinut cont ca patrunderea intensitatii campului electric in substrat depinde de diferenta dintre indicii de refractie. De aceea trebuie sa avem un contrast al indicilor de refractie cat mai mare posibil.O alta problema ar fi ca pentru orice tip de material folosit intensitatea campului electric se va extinde mai mult in substrat decat in aer si de aceea folosim mai multe geometrii aditionale pentru a confina modul in cavitate. O microcavitate de acest tip este prezentata in figura 16. Se foloseste un piedestal pentru a ridica cavitatea deasupra substratului. Acest lucru are ca efect izolarea cavitatii de substrat si reducerea pierderilor. O alta metoda de a reduce pirderile ar fi corodarea unor gauri mai adanci in ghidul de unda. Daca corodam niste gauri mai adanci in ghidul de unda astfel incat sa patrunda si in substrat, atunci o parte mai mare din campul electric este afectat de varatia periodica a indicelui de refractie. Astfel creste reflectivitatea "oglinzilor", pentru ca coloanele de aer se comporta ca niste oglinzi Bragg, si atunci se reduc pierderile. Mai multe materiale pot fi folosite pentru fabricarea acestor microcavitati. Si si SiO2 ofera un contrast al indicilor de refractie foarte bun, siliciu avand un indice de refractie de 3,48 si bioxidul de siliciu 1,44, pentru 1,55 μm. Ghidul este facut din Si, iar substratul este din SiO2. Adancimea coloanelor de aer este de doua ori grosimea ghidului, adica 1 μm.
Aceste cavitati au fost proiectate astfel incat modul rezonant din cavitate sa se cupleze eficient cu modurile TE din ghidul de unda. Modurile TM nu se cupleaza cu modul cavitatii. Pentru a proiecta un rezonator pentru modurile TM trebuie sa gasim o structura care sa aibe o banda interzisa pentru modurile polarizate in directie verticala. Ne amintim ca o banda interzisa larga, apare pentru modurile ghidate atunci cand doua benzi prezinta o diferenta intre cencentratia intensitatii campului electric in regiunile cu aer si cele cu dielectric. O structura de acest tip valabila pentru modurile TM este prezentata in figura 17. Intensitatea campului electric pentru prima banda se concentraza in jurul barelor din dielectric vecine doua cate doua, iar pentru cea de - a doua in interiorul zonelor cu aer.
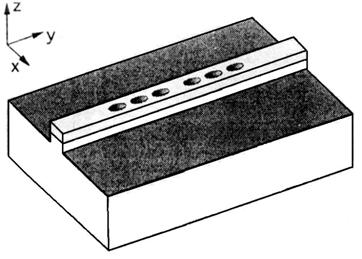
Figura 16.3 Microcavitate pe un substrat cu un indice de refractie scazut
Pentru a proiecta o structura care sa fie mai usor de fabricat, este necesar sa reducem inaltimea barelor. Insa daca barele sunt mai scurte atunci componenta longitudinala a intensitatii campului electric se mareste, iar banda intrezisa se micsoreaza. O imbunatatire adusa acestei structuri ar fi sa se conecteze toate varfurile barelor impreuna. Atunci intensitatea campului electric nu mai trece prin aer ci se concentraza in interiorul dielectricului, de unde rezulta ca prima banda s - ar situa mai jos, iar banda interzisa ar fi mai larga.

Figura 17.3 Microcavitate pentru modurile TM
In cazul microcavitatii pentru modurile ghidate TM, barele de dielectric pot avea diferite forme circulare, dreptunghiulare, eliptice, analog gaurile din microcavitatile pentru modurile ghidate TE, rezultatul obtinut avand ca efect aparitia de noi moduri rezonante in banda interzisa.
In concluzie in aceste doua subcapitole am prezentat aplicatiile cele mai importante ale cristalelor 1D, ghiduri de unda si microcavitati. Eficienta de transmisie este foarte buna, pentru ambele aplicatii, ghid de unda 1D 82% si ghid hibrid 1D 2D de 98,8% in cazul transmisiei modului fundamental, iar pentru microcavitati de 83% cu un factor de calitate Q = 271.
3 Cristale fotonice 2D
1 Materiale fotonice cu simetrie hexagonala
Orice structura periodica 3D ridica cateva probleme de fabricatie: contrastul dintre indicii de refractie trebuie sa fie mare ca difractia Bragg sa se produca, iar perioada de repetitie trebuie sa fie aproape de ordinul lungimii de unda, ceea ce face ca fabricarea cristalelor cu banda fotonica interzisa completa sa fie foarte dificila pentru frecvente din domeniul vizibil si infrarosu.
Acest lucru a determinat cercetatorii sa - si indrepte atentia catre structurile care sunt periodice in doar doua dimensiuni si uniforme in cea de - a trei - a. Printre tehnologiile care se aplica cu succes se numara: corodarea cu ioni reactivi a semiconductorilor si corodarea unei componente dintr - un material alcatuit din doua tipuri de sticla. Astfel rezulta o multitudine de gauri cu aer intr - un material gazda cu un indice de refractie mare. Teoretic si analiza acestor cristale este simpla, iar cand propagarea fluxului fotonic este restrictionat la planul transversal atunci se formeaza benzi fotonice interzise. Asemenea structuri au fost construite si rezultatele experimentale sunt in acord cu cele practice. Totusi aceste cristale nu au benzi fotonice interzise complete pentru ca in realitate fotonii se pot propaga liber in afara planului transversal, restrictia la planul transversal fiind artificiala. Cristalele 2D suprimeaza propagarea undelor electromagnetice in planul retelei, dar stoparea propagarii fotonilor in cea de a trei - a directie se poate obtine daca inseram cristalul intre doua oglinzi Bragg. Benzile interzise pentru modurile TE si TM trebuie sa se suprapuna unele peste atele pentru a forma o banda interzisa care sa opreasca propagarea fotonilor indiferent de tipul poalrizatiei. Dintre retelele Bravais 2D pentru o retea hexagonala zona Brillouin este aproape sferica ceea ce implica eixstenta unor benzi interzise destul de largi
In figura 18.3 e ilustrata o structura hexagonala 2D. Cele doua puncte A si B sunt ocupate de cilindrii cu raza ρ1 si ρ2, iar α este raportul razelor. Distanta dintre cele doua puncte este a. Daca α 0 avem o structura triunghiulara, daca α 1 clindrii au aceleasi raze si obtinem un aranjament bidimensional de hexagoane, numit structura de grafit. Daca α variaza intre 0 si 1 avem o intreaga clasa de structuri de nitrura de bor. Aceste cristale se caracterizeaza de doi parametrii factorul de umplere f si raportul razelor α. Cele mai largi benzi interzise de 7% si 4% s - au obtinut pentru structurile de nitrura de bor alcatuite din cilindrii de aer in GaAs cu un factor de umplere f %, iar 0,5 < α < 1. S - au examinat si structurile de nitrura de bor formate din bare de GaAs in aer si avem doua benzi interzise pentru 0,5 < α < 1, iar f 30%. Pentru structurile de grafit formate din bare de GaAs in aer banda interzisa cea mai larga de aproximativ 10% s - a obtinut pentru ρ 0,35a, iar f = 30%. Mai avem o banda interzisa pentru ρ 0,25a si f = 15%. Aceste structuri hexagonale 2D au benzi interzise destul de largi si sunt important de studiat datorita surapunerii benzilor pentru diferite polarizari

Figura 18.3 Structura 2D hexagonala
Pentru o retea cu simetrie triunghiulara sau patratica o banda fotonica interzisa 2D care sa fie indepndenta de polarizatie poate fi obtinuta numai cu o structura de "fagure de miere" cu coloane de aer
2 Structuri fotonice 2D in forma de fibra
S - a ajuns la concluzia ca cele mai largi benzi interzise pentru cristalele fotonice 2D rezulta daca structura este hexagonala.
Pentru a intelege pe deplin comportamentul structurilor periodice 2D este necesar sa consideram unde a caror vector de unda au o componenta longitudinala β. In figura 19 este prezentata o structura cu banda fotonica interzisa 2D, ale carui bare sunt aranjate in forma de fagure de miere si sunt uniforme in directie longitudinala [14].

Figura 19.3 Cristal fotonic 2D
Chiar daca aceste structuri nu prezinta benzi fotonice complete, totusi exista benzi fotonice interzise limitate in anumite directii. Pentru o frecventa care poate fi impusa folosind diferite fotodiode sau lasere, sunt valori interzise ale lui β pentru care nici o unda nu se propaga de - a lungul axei z chiar daca componentele din planul transversal al vectorului de unda kx si ky sunt reale.
Intr - un mediu uniform cu un indice de refractie n, numai valorile lui β mai mari decat kn (unde k = ω/c0) sunt interzise, astfel incat putem spune ca avem o banda fotonica interzisa pentru aceste valori ale lui β. Mai mult decat atat acest rezultat indreptateste fenomenul de reflexie totala interna pe baza caruia functioneaza fibrele optice. In figura 20 este prezentate conditiile pe care miezul fibrei trebuie sa le indeplineasca astfel incat fluxul de fotoni sa fie trasmis mai departe.

Figura 20.3 Fenomenul de reflexie totala interna
Materialul din care este realizat miezul are un indice de refractie n1 si este inconjurat de un alt material de protectie cu un indice de refractie n2. Fluxul de fotoni se poate propaga prin miez daca componenta longitudinala a vectorului de unda β este mai mica decat kn1. Daca β > kn2, atunci fluxul de fotoni nu trece de invelis si se propaga de - a lungul miezului. Spre deosebire, daca β are valori mai mici atunci fotonii pot scapa din miez, insa toate fibrele au inca un strat de protectie realizat de obicei dintr - un polimer cu indice mare de refractie care absoarbe sau refracta acesti fotoni. De aceea toate undele care nu sunt confinate in miez sunt absorbite de acest invelis, astfel incat numai undele din miez se deplaseaza de la un capat la celalat al fibrei se propaga. Pot exista mai multe benzi interzise pentru diferite valori ale lui β separate unele de altele de benzi permise. In functie de parametrii dimensionali se modifica si valoarea lui β si pozitiile benzilor interzise. Fotonii care au componenta longitudinala a vectorului de unda in interiorul benzii interzise nu se pot propaga in cristalul fotonic. Insa daca periodicitatea este intrerupta atunci, un anumit mod TE sau TM se cupleaza cu defectul si prin difractie Bragg se deplaseaza prin materialul fotonic. Defectul poate avea mai multe forme, cum ar fi indepartarea de unei portiuni dintr - o bara ca in figura 19. Daca structura periodica este inconjurata de un material cu un indice de refractie ridicat, atunci numai modurile defecte se propaga de la un capat la celalat al materialului fotonic cu banda interzisa. Structura joaca rolul unei fibre optice care ghideaza fluxul de fotoni pe baza difractiei Bragg si nu prin reflexie interna totala. Defectul este miezul fibrei, iar structura periodica este invelisul.
Pentru a fabrica o fibra de acest tip trebuie sa realizam o variatie periodica a indicelui de retractie. Din explicatiile teoretice din capitolele anterioare stim ca este mai avantajos sa avem regiuni izolate cu un indice de refractie mai mic intr - un material gazda cu un indice de refractie mai mare. Deoarece un cristal fotonic 2D cu simetrie hexagonala are cele mai largi benzi interzise s - a folosit un cristal de acest tip. S - a ajuns la concluzia ca cel mai potrivit material din care sa realizam o asemenea structura este bioxid de siliciul deoarece tehnologiile de lucru cu acest material sunt bine cunoscute, iar vascozitatea sa variaza gradual cu temperatura astfel incat procesul de tragere in fibra este mai simplu de controlat. Variatia indicilor de refractie necesara este oferita de gaurile cu aer din structura de unde rezulta un raport al indicilor de refractie de 1,45:1. Fabricarea cristalului fotonic in forma de fibra este un proces in mai multi pasi, deoarece dimensiunile transversale ale structurii trebuie reduse de la 30 mm la 2 μm. Acest proces este ilustrat in figura 21. Pentru fabricarea fibrei banda fotonica interzisa s - a pornit de la o bara cilindrica de bioxid de siliciu a) care, este frezata in exterior pana cand capata o forma hexagonala, iar in centru se face o gaura b). Aceste bare sunt puse unele peste altele pana cand structura capata o forma de fagure de miere c). In final structura este imbracata in bioxid de siliciu si trasa in fibra.
Se ridica intrebarea daca procesul de fabricatie este o reusita din punct de vedere mecanic sau nu. Este posibila asezarea barelor hexagonale unele peste altele fara ca ele sa intre unele in altele, gaurile de aer se deformeaza in timpul tragerii in fibra; raspunsul la aceste intrebari este afirmativ.
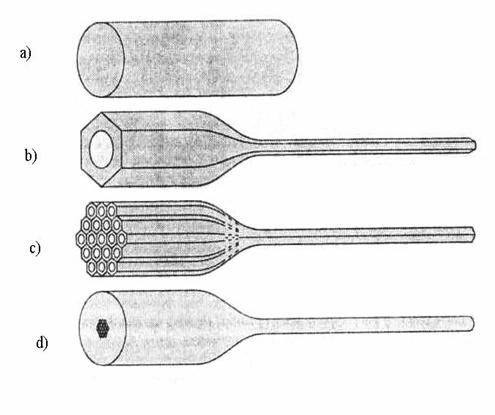
Figura 21.3 Procesul de fabricatie pentru fibra din cristal fotonic
S - a folosit o bara cilindrica din bioxid de siliciu cu diametrul de 30 mm si lunga de 250 mm. S - a facut o gaura centrala cu diametrul de 16 mm, iar exteriorul a fost frezat pana cand s - a obtinut o structura hexagonala in sectiune transversala. Asemenea procesului de realizare a fibrelor optice prin tehnica de filatura, largimea barei a fost redusa de la 30 mm la 1 mm astfel incat au rezultat cativa zeci de metrii de bara hexagonala. Aceasta a fost taiata din 250 in 250 mm, astfel incat 331 de bucati au fost aranjate in forma de fagure de miere, cu 11 bare de - a lungul fiecarei fete. Acum se poate face un defect la o bara, de exemplu neintroducand o bara sau lasand o bara fara gaura centrala. Barele hexagonale trebuie sa fie suficient de mari pentru a putea sa fie fixate unele langa altele. Toate barele au fost stranse cu un fir de talntal si au fost trase din nou in forma de bara hexagonala cu un diametru de 1 mm. Structura a fost inconjurata cu bare de bioxid de siliciu hexagonale si a fost trasa din nou prin procesul de filaj pentru rezultand fibra in forma finala. Imbracamintea de bioxid de siliciu din jurul barelor cu gauri este necesara pentru a face fibra suficient de mare pentru a fi manevrabila. Camasa de bioxid de siliciu din jurul barei hexagonale centrale e realizata tot din bare hexagonale cu un continut mai mare de apa de 1200 ppm OH fata de 120 ppm. Astfel barele de bioxid de siliciu din jur au o vascozitate mai mica ceea ce le va permite sa se imbine unele cu altele, iar gaurile din bara centrala sa nu se umple. Barele exterioare nu s - au imbinat prea bine insa gaurile nu s - au umplut cu bioxid de siliciu. Rezultatul final demonstreaza insa ca realizarea unei fibre din bioxid de siliciu si aer este posibila.
In concluzie am descris un cristal cu banda fotonica interzisa 2D facut din bare de bioxid de siliciu aranjate periodic intr - o retea de forma unui fagure de miere. Chiar daca nu prezinta o banda fotonica interzisa completa, exista anumite valori ale componentei longitudinale a vectorului de unda β pentrtu care fluxul de fotoni cu diferite lungimi de unda nu se pot propaga. Daca se introduce un defect in structura periodica care se poate numi miezul fibrei, atunci putem ghida fluxul de fotoni de - a lungul fibrei prin difractie Bragg.
3 Grilaje de difractie din cristale fotonice
In acest subcapitol voi prezenta o noua posibila aplicatie a cristalelor 2D si anume grilajele de difractie. Acest nou tip de grilaj este realizat dintr - un cristal fotonic cu simetrie hexagonala.
In figura 22.3 sunt prezentate doua grilaje din cristale fotonice. In partea stanga grialjul este alcatuie din bare circulare de dielectric de raza R in aer, iar in

Figura 22.3 Grilaje de difractie din cristal fotonic 2D
partea dreapta este
structura inversa din gauri cilindrice de aer intr - un material
gazda dielectric. Trebuie mentionat ca aceste grilaje sunt
compuse din doua parti in partea de jos a figurii
este un cristal fotonic 2D cu simetrie hexagonala si perioada d.
Materialul fotonic cu banda interzisa este considerat infinit de - a
lungul axei x, in timp ce de - a lungul axei y se limiteaza la Ng
nivele separate de o distanta ![]() Ng =
6 pentru figura noastra). Partea de sus este formata dintr - o retea cu
perioada dg Md unde M
este un numar natural. Aceasta structura este plasata la
distanta h fata de ultimul nivel al cristalului fotonic, barele
avand o raza R ,
iar materialul din care sunt facute are acelasi indice de
refractie ca si barele cilindrice ale cristalului fotonic.
Ng =
6 pentru figura noastra). Partea de sus este formata dintr - o retea cu
perioada dg Md unde M
este un numar natural. Aceasta structura este plasata la
distanta h fata de ultimul nivel al cristalului fotonic, barele
avand o raza R ,
iar materialul din care sunt facute are acelasi indice de
refractie ca si barele cilindrice ale cristalului fotonic.
Structura din partea dreapta alcatuita dintr - un material gazda dielectric in interiorul caruia sunt bare de aer circulare, distanta dintre partea superioara a dielectricului si barele cu raza R este ht si distanta dintre partea inferioara a materialului gazda si barele din cristalul fotonic este hb.
Pentru ca grilajele de difractie din cristale fotonice sa fie eficiente trebuie sa indeplineasca doua conditii legate de lungimea de unda prima caracterizeaza efectul de stralucire care se refera la stralucirea undei reflectate fata de unda incidenta pentru o anumita lungime de unda, iar cea de a doua se refera la existenta benzii fotonice interzise pentru lungimea de unda pentru care exista efectul de stralucire. In general cristalele fotonice prezinta benzi interzise pentru un interval de lungimi de unda mai mare decat perioada d a cristalului, centrul benzii interzise avand o valoare de 2d sau 3d. Ca o consecinta un grilaj care are aceeasi perioada ca si cristalul fotonic nu poate fi utilizat in regiunea unde au loc efectele de stralucire, adica pentru ordinul -1 de difractie care se propaga in directie inversa fata de unda incidenta.
Parametrii grilajului trebuie sa indeplineasca urmatoarea relatie
![]() (2)
(2)
unde dg este perioada grilajului, θ este unghiul de incidenta, iar λ este lungimea de unda. Intervalul de lungimi de unda care ne intereseaza si unde au loc efectele de stralucire este (2dg3, 2dg) unde sunt difractate doar doua ordine -1 si 0. Astfel daca perioada dg coincide cu perioada d a structurii fotonice, atunci zona de stralucire este sub banda fotonica interzisa. Cu alte cuvinte cand λ dg este mai mare ca 2 singurul ordin reflectat este ordinul zero care nu prezinta nici un interes in spectroscopie. De aceea dg = Md, relatia lui Littrow devenind
![]() (3)
(3)
astfel incat λ dg >
Grilajul din partea dreapta a figurii 22.3 este folosit pentru un flux fotonic s - polarizat, cristalul fotonic 2D are
benzi mai largi. Indicele de refractie al materialului dielectric este 3,
iar raza R a barelor cilindrice este 0,2 μm, rezultand o banda
fotonica interzisa intre λ = 1,9 μm si λ = 3,7
μm. Se considera d = 1 μm, M = 3, Ng = 5 si
distanta h = ![]() μm. S - au
realizat curbele de eficienta al grilajelor de acest tip,
parametrul modificat fiind R'de la 0,1; 0,12; 0,15; 0,17;
0,2; 0,25 μm, cu rezultate teoretice foarte bune. Ceea
ce este important de precizat este ca exista o regiune de
stralucire intre λ = 2 μm si λ = 3,5 μm dupa ce R μm cu valori maxime ale
eficientei de 99,96%. Deoarece aceasta valoare este determinata
de reflectivitatea cristalului fotonice atunci eficienta va fi suta
la suta daca vom mari pe Ng. Deoarece aceste
rezultate au fost obtinute fara sa se faca nici o
optimizare a parametrilor este de
asteptat sa se faca viitoare imbunatatiri pentru
aceste valori ale eficientei,
variind de exemplu parametrul h ajungand pana la 99,98%.
μm. S - au
realizat curbele de eficienta al grilajelor de acest tip,
parametrul modificat fiind R'de la 0,1; 0,12; 0,15; 0,17;
0,2; 0,25 μm, cu rezultate teoretice foarte bune. Ceea
ce este important de precizat este ca exista o regiune de
stralucire intre λ = 2 μm si λ = 3,5 μm dupa ce R μm cu valori maxime ale
eficientei de 99,96%. Deoarece aceasta valoare este determinata
de reflectivitatea cristalului fotonice atunci eficienta va fi suta
la suta daca vom mari pe Ng. Deoarece aceste
rezultate au fost obtinute fara sa se faca nici o
optimizare a parametrilor este de
asteptat sa se faca viitoare imbunatatiri pentru
aceste valori ale eficientei,
variind de exemplu parametrul h ajungand pana la 99,98%.
Pentru un flux de fotoni p - polarizati, cristalele
fotonice cu structura inversa prezinta benzi interzise cele mai
largi si de aceea vom considera cristalul fotonic din partea dreapta
a figurii 22. Pentru un material cu un indice de refractie 3 si
cu R mai mari de 0,32 μm se
obtin benzi fotonice destul de largi, aceasta valoare a razei fiind
adoptata pentru a rezulta o dimensiune nu prea mare pentru coloanele de
aer. Distanta ht = 0,43 μm astfel incat R sa
poata avea valori destul de mari. Ceilalti parametrii structurali
sunt Ng = 5 si distanta h = ![]() μm, rezultand o
banda fotonica interzisa intre λ = 3 μm si λ = 4,2 μm astfel inca a fost
necesar M = 3 pentru ca banda fotonica si zona de stralucire
sa fie cat mai apropiate. S - a determinat eficienta grilajului in
functie de lungimea de unda, parametrul modificat fiind R' = 0.25; 0.32; 0.4 μm.
Eficienta grilajelor din cristale fotonice pentru un flux fotonic p -
polarizat nu este destul de mare, maxim 90% pentru R = 0,32
μm, si nu rezulta nici un efect de stralucire. Pentru a
imbunatatii eficienia grilajului s - au facut unele
modificari. S - a
mentinut M = 3 dar h = 0,41 μm fata de h = 0,86 μm.
Deoarece R nu
se mai poate mari peste 0,4 μm, atunci pentru a creste
dimensiunea barelor se inlocuieste forma circulara cu una
eliptica. Lungimea semiaxei paralele cu axa y ramane egala cu 0,4 μm, adica a = 0,4 μm,
iar semiaxa paralela cu axa x este modificata intre 0,4 μm
pana la 1,2 μm. S - a calculat eficienta grilajului in
functie de lungimea de unda, modificandu - se b = 0,4 μm.
Eficienta maxima care se obtine e determinata in primul
rand de reflectivitatea cristalului fotonic si rezulta pentru valori
ale lui b mai mici de 0,8 μm. Aceasta valoare este de 99,5% rezultate
mai bune s - ar obtine daca marim Ng.
μm, rezultand o
banda fotonica interzisa intre λ = 3 μm si λ = 4,2 μm astfel inca a fost
necesar M = 3 pentru ca banda fotonica si zona de stralucire
sa fie cat mai apropiate. S - a determinat eficienta grilajului in
functie de lungimea de unda, parametrul modificat fiind R' = 0.25; 0.32; 0.4 μm.
Eficienta grilajelor din cristale fotonice pentru un flux fotonic p -
polarizat nu este destul de mare, maxim 90% pentru R = 0,32
μm, si nu rezulta nici un efect de stralucire. Pentru a
imbunatatii eficienia grilajului s - au facut unele
modificari. S - a
mentinut M = 3 dar h = 0,41 μm fata de h = 0,86 μm.
Deoarece R nu
se mai poate mari peste 0,4 μm, atunci pentru a creste
dimensiunea barelor se inlocuieste forma circulara cu una
eliptica. Lungimea semiaxei paralele cu axa y ramane egala cu 0,4 μm, adica a = 0,4 μm,
iar semiaxa paralela cu axa x este modificata intre 0,4 μm
pana la 1,2 μm. S - a calculat eficienta grilajului in
functie de lungimea de unda, modificandu - se b = 0,4 μm.
Eficienta maxima care se obtine e determinata in primul
rand de reflectivitatea cristalului fotonic si rezulta pentru valori
ale lui b mai mici de 0,8 μm. Aceasta valoare este de 99,5% rezultate
mai bune s - ar obtine daca marim Ng.
In concluzie am demonstrat ca grilajele de difractie din cristale fotonice cu bada interzisa ofera efecte de stralucire cu o eficienta de aproape 100% pentru ambele polarizatii. Curbele de eficienta pentru aceste noi tipuri de grilaje au o forma similara cu cele ale grilajelor clasice, pentru un flux fotonic s - polarizat, spre deosebire de un flux fotonic p - polarizat, ale carui curbe de eficienta nu se ridica la nivelul grilajelor clasice. Explicatia acestui comportament diferit poate fi excitarea modurilor ghidate la partea de deasupra a grilajului cu contrast inversat, intre grila superioara a cristalului fotonic si planul de interfata superior. Este bine cunoscut ca propagarea undelor de suprafata sau ghidate duc la aparitia unor defecte care pot deteriora efectul de stralucire al grilajelor clasice. Pentru a inbunatatii curbele de eficienta pentru fluxul fotonic polarizat si nepolarizat ar putea fi interesant sa folosim si alte tipuri de cristale fotonice. Obtinerea unor curbe de eficienta cu maxime aproape de 100% pentru un flux fotonic nepolarizat ar necesita benzi fotonice interzise complete, adica sa folosim cristale fotonice cu simetrie de grafit. Putem de exemplu sa introducem scaderi bruste ale eficientei indepartand anumite bare din cristalul fotonic, proprietate care ar fi utilizata pentru filtrajul fluxului de fotoni.
Aceasta noua aplicatie a cristalelor fotonice si anume realizarea grilajelor de difractie este la inceput si cercetarile nu sunt inca finalizate. Rezultatele nu au fost obtinute folosind diferite optimizari pentru fotonii s - polarizati, spre deosebire de grilajele pentru fotonii p - polarizati unde au fost necesare cateva imbunatatiri ale parametrilor astfel incat sa avem o eficienta foarte buna. Cercetarile continua astfel incat sa avem o eficienta a grilajelor de difractie din cristale fotonice foarte aproape de suta la suta, deoarece aceste griaje au un rol vital in multe domenii ale stiintei si tehnologiei incluzand spectroscopia, astronomia, pentru lasere de mare putere sau pentru filtre.
4 Lasere DFB si ghiduri de unda din cristale fotonice 2D
Chiar daca controlul asupra fluxului de fotoni intr - un cristal 2D nu este complet ca in cazul cristalelor 3D, este posibil sa fabricam o varietate de dispozitive. Alte aplicatii ale cristaleor 2D in afara celor prezentate mai sus, includ un nou tip de laser cu reactie pozitiva distribuita multidirectionala, DFB (distributed feedback).
Laserele DFB cu cristale fotonice genereaza la iesire un fascicol de fotoni cu o stabilitate mai buna si pentru o gama de lungimi de unda mai precise decat laserele DFB obisnuite. Principiul de functionare al laserelor DFB este urmatorul: laserele DFB contin un grilaj care datorita reactiei pozitive conduce la un castig pentru o lungime de unda care depinde de perioada grilajului. Cristalele fotonice ne permit sa proiectam lasere DFB multidirectionale, cu o suprafata emitatoare mai mare si cu largimi de lungimi de unda mai inguste.
Un asemenea dispozitiv a fost realizat utilizandu - se un
cristal fotonic 2D in care au fost integrate doua plachete A si B
folosindu - se tehnica de fuzionare a plachetelor. Prima placheta e
formata dintr - un strat activ cu gropi cuantice multiple de InGaAs InP, λ
= 1,3 μm, crescut pe un substrat de InP de tip p. Placheta B este
alcatuita dintr - o structura cu o retea triunghiulara
pe un substrat de InP de tip n. Acest laser este prezentat in figura 2 Perioada
retelei triunghiulare in directia Γ
- Χ este proiectata astfel incat sa coincida cu lungimea de
unda a fotonilor emisi de stratul activ, astfel incat mai are loc
inca un proces DFB in directia Γ - Χ. Reactia
distribuita pozitiva care e determinata de reteaua
triunghiulara conduce la o serie de efecte foarte interesante. Structura
triunghiulara periodica prezinta 6 directii Γ - Χ
echivalente, astfel incat fotonii care se propaga pe directii Γ
- Χ individuale sunt difractati nu numai inapoi ci si in
celelate 4 directii Γ - Χ (![]() 60s,
60s, ![]() 120s). Cu alte cuvinte 6 unde se cupleaza unele cu
altele. Rezultatul consta intr - un cuplaj coerent dintre 6 unde care se
propaga in directii Γ - Χ echivalente si are loc o
oscilatie laser
120s). Cu alte cuvinte 6 unde se cupleaza unele cu
altele. Rezultatul consta intr - un cuplaj coerent dintre 6 unde care se
propaga in directii Γ - Χ echivalente si are loc o
oscilatie laser

2D.
Figura 23 Laser DFB dintr - un cristal fotonic 2D (deasupra) care ii confera multidirectionalitate datorita efectului retelei triunghiulare
Fluxul de fotoni se cupleaza si in afara planului retelei triunghiulare, perpendi-cular pe substrat deoarece conditia lui Bragg este indeplinita si in aceasta directie. Cristalul fotonic controleaza nu numai modurile longitudinale, ca laserele DFB liniare, dar si pe modurile laterale. Astfel ne asteptam ca acest dispozitiv sa functioneze ca un laser de mare putere care poate oscila intr - o suprafata bidimensionala destul de larga.
Materialele fotonice cu banda interzisa 2D pot fi folosite ca ghiduri de unda daca se face un defect in linie in interiorul cristalului ca in figura Mai mult, defectele punctuale sunt cavitati ca in figura 2, iar cu o combinatie de aceste defecte rezulta niste dispozitive foarte folositoare in diverse aplicatii. Sa consideram un cristal fotonic 2D cu simetrie triunghiulara. Banda fotonica interzisa confineaza fluxul de fotoni in planul transversal, iar contrastul dintre indicii de refractie confineaza fluxul in directie verticala. Putem proiecta un dispozitiv care sa fie alcatuit dintr - un ghid de unda si doua cavitati i si j. Defectul liniar este un ghid de unda care are o eficienta de aproape suta la suta. Fiecare defect punctual joaca rolul unei cavitati care poate capta fotoni cu o anumita lungime de unda. Lungimea de unda corespunzatoare fotonilor prinsi in cavitate depinde de dimensiunea defectului. Defectul este o cavitate care se cupleaza cu un anumit mod rezonant. Cu alte cuvinte daca modificam dimensiunea defectului atunci modul rezonant cu care se cupleaza cavitatea isi schimba frecventa. Fotonii prinsi in cavitate sunt emisi in directie verticala. Acest dispozitiv a fost fabricat, iar rezultatele experimentale au demonstrat cum aceste defecte punctuale se cupleaza cu fotoni cu o anumita lungime de unda respectiv λi si λj si apoi sunt emisi in directie verticala, normal la cristal.

Figura 24.3 Dispozitiv alcatuit dintr - un ghid de unda cu defecte punctuale
Ghidul de unda este cuplat la o fibra optica cu o lentila, din partea dreapta, iar sursa de fotoni este un laser acordabil din semiconductor care lucreaza in regiunea 1,55 μm. S - a folosit o camera de vederi in infrarosu pentru a monitoriza capturarea si emisia fotonilor. Cand laserul a fost acordat la 1,545 μm defectul j emitea un flux puternic de fotoni, dar defectul i nu emitea deloc. Pe de alta parte la 1,566 μm defectul j nu mai emite spre deosebire de cavitatea i care emite puternic.
Pe baza acestui principiu este posibil sa creeam
un dispozitiv care emite sau nu un flux fotonic cu o anumita lungime de
unda, adaugand fibre optice deasupra cristalului fotonic pentru a
colecta fotonii emisi. Acest dispozitiv este foarte compact in sensul
ca latimea ghidului de unda impreuna cu defectele
punctuale este de aproape 10 μm si distanta dintre defectele
punctuale este de 4 μm, astfel incat un dispozitiv pentru 100 de lungimi
de unda ar avea o dimensiune de 10 ![]() 400 μm2.
400 μm2.
Acest dispozitiv care este ca un fel de comutator in functie de lungimea de unda este unul din numeroasele aplicatii ale cristalelor fotonice care au la baza aceasta localizare puternica a fotonilor in raport cu un defect.
5 Microcavitati din cristale fotonice 2D
Cristalele fotonice 2D au utilizari foarte diverse si de aceea multi cercetatori vad in aceste materiale viitorul optoelectronicii.
Vom investiga proprietatile unei microcavitati intr - un cristal fotonic 2D. Cristalul este alcatuit din mai multe bare de dielectric foarte lungi asezate intr - o retea patrata de lungime a. Fiecare coloana are o raza de 0,20a si un indice de refractie de 3,4. Normalizand fiecare parametru in raport cu constanta de retea a, putem scala microcavitatea la orice dimensiune. Vom vedea cum se propaga undele electromagnetice in planul normal la bare. Deoarece aceste coloane au simetrie de translatie de - a lungul axelor, undele se decupleaza in doua tipuri de moduri polarizate transversal TE si TM, in functie de campul electric sau magnetic normal la bare. Acest cristal prezinta o banda interzisa larga pentru modurile TM intre frecventele 0,29 c/a si 0,42 c/a. Cristalul nu are o banda interzisa pentru modurile TE si de aceea vom studia numai modurile TM.
Acum introducem un defect in aceasta structura exacta. Defectul poate avea orice forma si marime, poate rezulta prin modificarea indicelui de refractie a unei bare sau prin schimbarea razei sau indepartand o bara complet ca in figura 25.
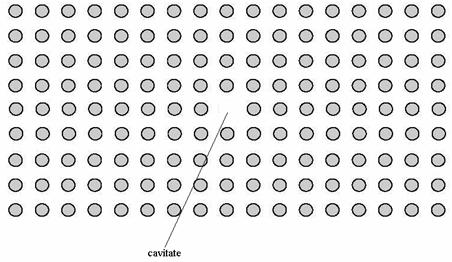
Figura 25.3 Microcavitate in cristal 2D
Modificam raza unei singure bare. Reducem treptat aceasta raza, iar cand atinge valoarea de 0,15a un mod rezonant apare in vecinatatea defectului. Deoarece defectul presupune indepartarea de material dielectric din cristal modul are o frecventa aproape de partea inferioara a benzii interzise. Pe masura ce raza este micsorata si mai mult frecventa modului rezonant urca in banda interzisa si atnge un maxim de 0,38 c a cand bara este indepartata complet. De unde rezulta ca frecventa modului rezonant poate fi modificata in functie de dimensiunea barelor.
Este posibil sa marim dimensiunea razei in loc sa o micsoram. Din nou pornind de la un cristal perfect, crestem gradual raza coloanelor. Deoarece defectul presupune adaugarea de material, modurile apar din partea superioara a benzii interzise, iar cand raza depaseste 0,4a modurile dispar din banda interzisa.
Putem sa studiem si eficienta la cuplaj pentru un defect care presupune indepartarea unei bare din structura, dar pentru a cupla energie in cavitate trebuie sa transferam energia prin peretii cristalului. Un flux incident de fotoni poate transfera energie modului rezonant datorita campurilor evanescente de la suprafata cristalului. Modul rezonant are simetrie para in raport cu planul (x,y) care trece prin mijlocul defectului deoarece campul electric e polarizat de - a lungul directiei z. Se trimite un impuls gausian spre cristal. Profilul gausian este centrat la frecventa 0,35 c a si are o latime de 0,20 c a, care depaseste frecventele limita ale benzii interzise. Spectrul de transmisie normalizat la amplitudinea incidenta este prezentat in figura de mai jos.

Figura 26.3 Spectrul transmisiei prin cavitate
Dupa cum se vede in spectrul de transmisie exista o zona unde nu se transmite nimic, intre frecventele 0,24 c/a si 0.42c/a, Modurile din interiorul zonei unde nu se transmite nimic sunt puternic atenuate, nu se pot propaga prin cristal si sunt reflectate inapoi. Pe de alta parte modurile din afara acestei regiuni sunt transmise foarte eficient, unele frecvente au coeficientul de transmisie aproape de unitate, adica aceste moduri au putine pierderi datorita reflexiilor si imprastierii. Varful din interiorul zonei interzise de transmisie corespunde eficientei cuplajului radiatiei incidente cu modul rezonant, dar nu depaseste 50%.
Factorul de calitate Q este o masura a pierderilor din cavitate. Deoarece reflectivitatea cristalului din jurul defectului se mareste cu numarul de bare, atunci Q va creste odata cu marirea dimensiunii cristalului. Valoarea lui Q in functie de dimensiunea cristalului se mareste exponential cu numarul de bare din cristal. S - a determinat o valoare a lui Q de aproape 104 cu 4 randuri de bare de o parte si de alta a defectului, ceea ce confirma presupunerile si rezultatele anterioare. Deoarece avem pierderi de energie prin marginile cristalului, Q nu se satureaza chiar si pentru un numar mare de bare.
In concluzie o alta aplicatie importanta a cristalelor 2D este microcavitatea, care s - a obtinut prin indepartarea unei bare de dielectric din interiorul structurii. Eficienta la cuplaj este destul de mica deoarece s - a calculat intr - un singur punct in spatiu dar, factorul de calitate are valori foarte bune, fara sa se satureze pentru o dimensiune prea mare a cristalului.
Am prezentat in acest subcapitol cateva din aplicatiile cristalelor fotonice 2D, fibra fotonica, grilaje de difractie, lasere DFB, comutatoare. Ceea ce este caracteristic acestor utilizari si foarte important de retinut este eficienta foarte buna si pierderile foarte mici. Fibra are o atenuare de 0,1 dB km si putem transmite si impulsuri laser de mare putere fara ca structura sa se defecteze. Eficienta grilajelor de difractie este de 99,98%. Multe grupuri de cercetatori investigheaza crsitalele fotonice 2D deoarece sunt mai simplu de fabricat si au numeroase aplicatii in diferite domenii ale stiintei si tehnicii.
|
Politica de confidentialitate |
| Copyright ©
2024 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |