Rezolutia energetica a unui detector
a. Notiuni generale. Functia de raspuns G(E,U) a unui detector care lucreaza in regim de impulsuri este definita ca distributia semnalelor dupa amplitudinea U, pentru o energie E data a particulelor ce intra in detector. In multe cazuri aceasta este o functie Gauss: cazul semnalelor provocate de particule incarcate de aceeasi energie, pe baza efectelor de ionizare intr-un detector cu gaz, detector cu scintilatie sau semiconductor. Exista si alte distributii pentru semnalele U. Largimea minima a functiei G(E,U) este definita de o serie de factori. Cand energia particulelor se masoara dupa efectele de ionizare, largimea minima este determinata de caracterul statistic al pierderii de energie in substanta, adica de fluctuatiile numarului de purtatori de sarcina, si in cazul scintilatorului de fluctuatiile numarului de fotoni.
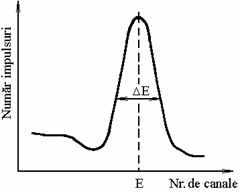
Fig. 2.50 Alegerea lui ![]() pentru picul de la energia E
pentru picul de la energia E
in vederea calcularii rezolutiei energetice ![]()
Rezolutia energetica h a unui detector se defineste ca raportul largimii ΔE la semiinaltime (fig. 2.50) a functiei G(E,U) pentru U fixat fata de valoarea E a maximului distributiei. Evident rezolutia energetica poate fi exprimata si ca raportul semilargimii ΔU la semiinaltime a functiei G(E,U) luata pentru energia radiatiei E fixe, dupa relatia:
![]()
unde amplitudinea semnalului U este functie de energie, U=f(E). Daca semnalul este proportional cu energia particulelor atunci:
![]()
Rezolutia energetica exprima posibilitatea de a deosebi doua radiatii dupa energie, cand aceste energii sunt apropiate.
Sa presupunem ca in detector
patrund doua grupe de particule cu energiile E1 si
respectiv E2, care dau doua distributii de semnale, cu
valorile medii ![]() . Daca
. Daca ![]() , cele doua grupe nu pot fi practic separate. Vom dovedi
aceasta afirmatie presupunand ca functia de raspuns
este o gaussiana. In aceasta situatie, probabilitatea de
aparitie a unor semnale U pentru particulele cu energia E1
este:
, cele doua grupe nu pot fi practic separate. Vom dovedi
aceasta afirmatie presupunand ca functia de raspuns
este o gaussiana. In aceasta situatie, probabilitatea de
aparitie a unor semnale U pentru particulele cu energia E1
este:
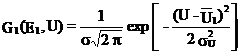
iar pentru particulele de energie E2:
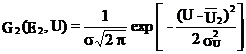
Daca notam ![]() , cele doua probabilitati devin:
, cele doua probabilitati devin:
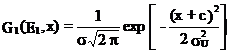
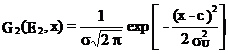
Probabilitatea totala ca sa inregistram semnale U fie de la particulele cu energia E1, fie
de la cele cu energia E2, va fi:
![]()
Functia G(E,x) va avea un singur
maxim daca ![]() si doua
maxime daca
si doua
maxime daca ![]() . Conditia
. Conditia ![]() , ne va da limita
, ne va da limita ![]() pentru care cele
doua energii mai pot fi separate. Se obtine pentru aceasta:
pentru care cele
doua energii mai pot fi separate. Se obtine pentru aceasta:
![]()
Deci in cazul ![]() avem doua maxime
in distributie si cele doua energii mai pot fi separate.
Mentionand ca pentru o distributie gaussiana largimea
la semianaltime ΔU se defineste in functie de abaterea
standard σU prin relatia:
avem doua maxime
in distributie si cele doua energii mai pot fi separate.
Mentionand ca pentru o distributie gaussiana largimea
la semianaltime ΔU se defineste in functie de abaterea
standard σU prin relatia: ![]() , obtinem ca pentru separare a doua energii
este necesar:
, obtinem ca pentru separare a doua energii
este necesar:
![]()
De asemenea relatia (2.105) devine:
![]()
Dispersia σ2 pentru detectorii in care energia se determina pe baza numarului de ioni (camera de ionizare), pe baza perechilor de purtatori (semiconductori) sau a numarului de fotoni (scintilatori) se poate afla in ipoteza ca toate actele de ionizare (de formare a purtatorilor) sunt independente una de alta si se supun distributiei Poisson. Daca N este numarul de perechi de purtatori (electron-gol, electron-ion) atunci σ2 = N. Notand cu ε energia medie pierduta de particula cu energie E pentru formarea unei perechi de purtatori, obtinem din (2.113):
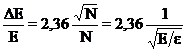
Totusi presupunerea ca actele de interactie sunt independente nu este adevarata. In camera de ionizare, particulele incarcate pierd energie pe intreg parcursul prin ionizare si excitare. Daca energia pierduta prin ionizare ar fi fost bine definita si probabilitatea de excitare
ar
fi zero, atunci fluctuatia numarului de perechi de ioni ar fi fost
±1. Daca probabilitatea de ionizare este mult mai mica decat
probabilitatea de excitare, procesul de ionizare poate fi socotit ca format din
acte independente si σ2=N. Se obtine insa in
aceasta presupunere o abatere standard mult mai mare decat cea
experimentala. De aceea se introduce un coeficient, numit factorul lui
Fano (F) care se defineste ca raportul dintre dispersia experimentala
si
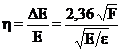
Aceasta rezolutie minima este de obicei alterata de zgomotul detectorului si al electronicii asociate. Deteminarea experimentala a rezolutiei concrete a unei instalatii se face trasand distributia semnalelor obtinute la iradierea detectorului cu particule monoenergetice. Pentru obtinerea acestui spectru, largimea canalului analizorului trebuie sa fie de cateva ori mai mica decat largimea functiei G(E,U) la semianaltime.
b. Detectori cu gaz. In cazul camerelor de ionizare, factorul Fano F are de obicei o valoare in jurul lui 0,7. Valoarea minima a rezolutiei energetice, data de relatia (2.113) poate fi atinsa daca toate particulele incarcate care ionizeaza gazul se opresc in zona sensibila a camerei
si lipsesc efectele de inductie. Aceste efecte pot fi reduse prin utilizarea unei camere cu grila si prin marirea constantei de timp in jurul valorii RC~10-3sec.
Pentru contorul proportional, rezolutia minima (2.113) este largita datorita fluctuatiilor factorului de multiplicare M. Abaterea standard relativa pentru factorul de multiplicare este:
![]()
unde se considera ca apar initial N perechi de ioni si se colecteaza MN electroni de catre firul central. In acest caz rezolutia energetica nu poate fi mai buna de:
![]()
Astfel, pentru energii ale particulelor de cca 1 MeV, rezolutia energetica este de aproximativ 3%.
c. Detectori cu scintilatii. Numarul de electroni ce sunt colectati de anod este dat de relatia:
![]()
unde A este un factor constant de proportionalitate fara dispersie, N este numarul de fotoni ce apar in scintilator, p este probabilitatea ca un foton aparut in scintilator sa produca un electron care sa ajunga pe prima dinoda si M este factorul de multiplicare.
Considerand ca U~Ne si ca toti factorii sunt independenti, atunci conform teoremei de propagare a erorilor rezulta pentru abaterea standard a tensiunii:
![]()
sau
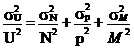
si rezolutia energetica devine:
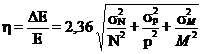 (2.121)
(2.121)
Primul termen din partea dreapta a relatiei (2.121) se evalueaza rapid, fiind 1/N. Cel de al doilea termen se determina de obicei experimental pentru fiecare detector in parte. Pentru a
calcula
pe ![]() reamintim ca:
reamintim ca:
![]()
unde δi este factorul de multiplicare al dinodei i, δi=δ, iar m este numarul de dinode. La dinoda k sosesc Npδk-1 electroni, iar aceasta va emite Npδk electroni cu dispersia Npδk. Aplicand teorema de propagare a erorilor putem scrie dispersia factorului de multiplicare:
![]()
unde
![]() este dispersia
multiplicarii diodei j. Din relatia evidenta:
este dispersia
multiplicarii diodei j. Din relatia evidenta:
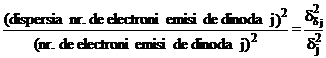
rezulta ca 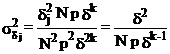
Introducand (2.124) si derivata lui M in (2.123) obtinem:
![]()
Deci:
![]()
Relatia (2.126) arata ca principala contributie in dispersia numarului de electroni ce ajung la anodul fotomultiplicatorului este data de dispersia coeficientului emisiei secundare pentru prima dinoda cat si de valoarea acestuia. De aceea pentru a micsora puternic dispersia numarului de electroni si deci, implicit a amplitudinii semnalului de tensiune, aproape in toti fotomultiplicatorii moderni se folosesc pentru prima dinoda materiale cu putere de emisie ridicata si se aplica intre fotocatod si prima dinoda tensiuni mari comparativ cu tensiunile aplicate intre celelalte dinode.
Introducand (2.126) in (2.121) obtinem:
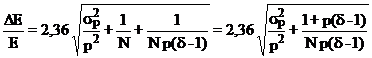
Deoarece numarul de fotoni produsi in scintilator este proportional cu energia particulei incarcate stopate in acesta, iar restul de marimi din formula (2.127) sunt constante ale fotomultiplicatorului, rezolutia energetica mai poate fi scrisa astfel:
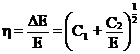
unde 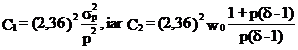 . Considerand p ≈ 0,05, pentru valoarea medie 5,
iar pentru energia w0 cheltuita de radiatia incidenta
in scintilator in vederea producerii unui foton o valoare in jur de 50 eV,
rezulta C2=1,67.10-3MeV. Pentru cristalele NaI(Tl)
foarte bune C1=2.10-4, si deci rezolutia
energetica este definita astfel:
. Considerand p ≈ 0,05, pentru valoarea medie 5,
iar pentru energia w0 cheltuita de radiatia incidenta
in scintilator in vederea producerii unui foton o valoare in jur de 50 eV,
rezulta C2=1,67.10-3MeV. Pentru cristalele NaI(Tl)
foarte bune C1=2.10-4, si deci rezolutia
energetica este definita astfel:
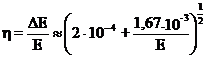
Pentru cristale de
NaI(Tl) se obtine ![]() in cazul
detectarii unor electroni cu energie de 100-150keV. Rezolutia se
imbunatateste pentru energii de 2-4MeV, atingand valori
in cazul
detectarii unor electroni cu energie de 100-150keV. Rezolutia se
imbunatateste pentru energii de 2-4MeV, atingand valori
de 4-5%. Relatiile de mai sus se verifica foarte bine experimental sub forma unei drepte in functie de Eγ-1/2:
![]() (2.130)
(2.130)
In fig. 2.47 este prezentata dependenta rezolutiei energetice experimentale de energia fotonilor pentru un cristal de NaI(Tl). Din dreapta obtinuta se pot estima constantele a si b.
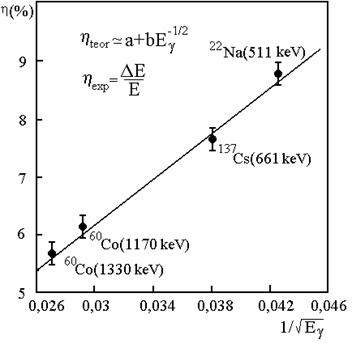
Fig. 2.51 Dependenta rezolutiei energetice
experimentale de energia fotonilor Eγ pentru NaI(Tl)
d. Detectori cu semiconductori. Considerand ca particulele incarcate care patrund in zona sensibila a detectorului sunt monoenergetice si ca pierd practic toata energia in aceasta zona, rezolutia energetica este data de relatia:
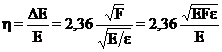
De unde pentru semilargimea energetica E se obtine relatia:
![]()
Factorul Fano determinat atat teoretic cat si experimental este in jur de 0,28 pentru siliciu si de 0,33 pentru germaniu.
Cu aceste valori , rezolutia energetica a unui detector cu siliciu exprimata in procente, se poate calcula dupa relatia:
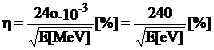
O relatie aproape identica se
poate folosi si pentru un detector cu germaniu. Folosind relatia
(2.133) se obtine o rezolutie energetica ![]() cu o semilargime
energetica ΔE=2,4keV pentru o radiatie incidenta de energie
egala cu 1 MeV. Pentru aceeasi radiatie incidenta,
rezolutia energetica a unui detector de NaI(Tl) calculata cu
relatia (2.129) este de 4,32%, adica de 18 ori mai slaba in
comparatie cu rezolutia energetica a unui detector cu
semiconductor. Rezolutia energetica definita de relatia
(2.133) este fireste o rezolutie optima. In realitate
rezolutia energetica este inrautatita de
alti factori ca: existenta curentilor de scurgere in volum
si la suprafata, colectarea incompleta a purtatorilor
de sarcina etc. Influenta acestora nu este totusi
esentiala. Astfel in cazul exemplului dat anterior, rezolutia se
modifica de la 0,24% la ~0,4%, ramanand in continuare foarte
buna si net superioara celorlalte tipuri de
cu o semilargime
energetica ΔE=2,4keV pentru o radiatie incidenta de energie
egala cu 1 MeV. Pentru aceeasi radiatie incidenta,
rezolutia energetica a unui detector de NaI(Tl) calculata cu
relatia (2.129) este de 4,32%, adica de 18 ori mai slaba in
comparatie cu rezolutia energetica a unui detector cu
semiconductor. Rezolutia energetica definita de relatia
(2.133) este fireste o rezolutie optima. In realitate
rezolutia energetica este inrautatita de
alti factori ca: existenta curentilor de scurgere in volum
si la suprafata, colectarea incompleta a purtatorilor
de sarcina etc. Influenta acestora nu este totusi
esentiala. Astfel in cazul exemplului dat anterior, rezolutia se
modifica de la 0,24% la ~0,4%, ramanand in continuare foarte
buna si net superioara celorlalte tipuri de 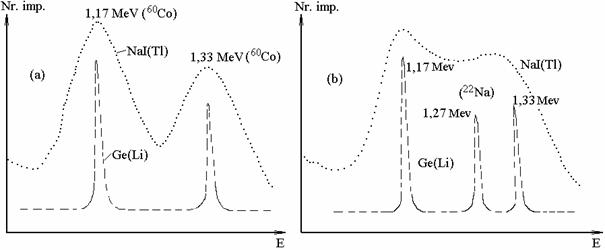 detectori.
detectori.
Fig. 2.48 Exemple comparative de spectre privind rezolutia energetica a unui detector Ge(Li) si aI(Tl)
|
Politica de confidentialitate |
| Copyright ©
2024 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |