
Sectiunea eficace este o marime importanta in obtinerea de informatii asupra dinamicii ciocnirilor nucleare la diferite energii . Notiunea de sectiune eficace este strans legata de caracterizarea proceselor de interactie dintre sisteme nucleare de naturi diferite si avand proprietati din cele mai diferite. O definitie generala a sectiunii eficace este destul de dificila [49,50]. Se accepta, in general, idea ca este probabilitatea de realizare a unei anumite interactii, valoarea sa depinzand de natura sistemelor nucleare care participa la ciocnire si de energia incidenta, cu luarea in considerare a ipotezei formei sistemelor nucleare care interactionaeza. De aceea, unitatea de masura este legata de sectiunea geometrica normala a procesului de interactie dintre doua sfere. Unitatea de masura tolerata se numeste barn si ia in considerare dimensiunile specifice sistemelor nucleare, anume: 1 barn = 10-28 m2 = 100 Fm2.
Sectiunea eficace mai poate fi considerata ca un coeficient specific interactiei. Astfel, sectiunea unei entitati tinta, s, pentru o interactie produsa de un sistem nuclear incident, cu sarcina sau fara sarcina, este definita ca raportul dintre probabilitatea de interactie pentru entitatea tinta considerata, P, si fluenta sistemelor nucleare incidente, F, anume:
![]() . (II.38)
. (II.38)
Fluenta reprezinta numarul de particule incidente, dN, pe o sfera care are aria sectiunii da. . Definitia sectiunii eficace data de relatia (II.38) este valabila daca probabilitatea P indeplineste conditia urmatoare: P << 1.
Trebuie mentionat faptul ca termenul de interactie se refera la orice proces in care energia si/sau directia particulei incidente este modificata sau particula incidenta este absorbita. În urma interactiei sunt emise una sau mai multe particule secundare.
Asa cum s-a vazut, definirea distributiei de multiplicitate in termenii teoriei probabilitatilor s-a facut cu ajutorul sectiunilor eficace totale si sectiunilor eficace partiale. În descrierea fenomenelor de producere multipla de particule aceste sectiuni, impreuna cu sectiunea eficace topologica si sectiunea eficace diferentiala, au un rol important . Utilitatea acestor marimi este legata de dependentele lor de energia de ciocnire, de natura sistemelor care participa la ciocnire, de tipul particulelor generate [4,51,52].
Sectiunea eficace totala, st, este definita ca sectiunea de creare a tuturor particulelor permise de legile de conservare intr-o ciocnire data, la o energie data. Acest tip de sectiune creste lent cu cresterea energiei pentru diferite sisteme nucleare care se ciocnesc.
Sectiunea eficace partiala, sn, da numarul de particule de un anumit tip, produse la o energie data. De aceea, acest tip de sectiune prezinta dependente de numarul de particule si de tipul de particula considerat. Sectiunea eficace partiala prezinta un maxim in vecinatatea energiei de prag pentru producerea tipului de particula considerat. Cresterea numarului de particule deplaseaza maximul spre energii mai mari.
Sectiunea eficace totala este data de suma tuturor sectiunilor eficace partiale, anume:
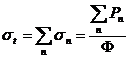 . (II.39)
. (II.39)
Sectiunea eficace topologica sch, descrie producerea unui anumit numar de particule cu sarcina in starea finala a unei ciocniri la o energie data. În acest caz, numarul particulelor cu sarcina, nch, este o variabila aleatoare, iar producerea unui anumit numar de particule cu sarcina, in starea finala, este un eveniment aleator. De aceea, descrierea sectiunii eficace topologice se face, pentru multiplicitati relativ mici, cu o distributie de probabilitate de tip Poisson, iar pentru multiplicitati mari cu o distributie de probabilitate de tip Gauss.
Daca numarul de particule cu sarcina din starea finala este fixat si se variaza energia de ciocnire, atunci sectiunea eficace topologica creste cu energia pana la o anumita valoare a energiei de ciocnire, apoi scade lent cu cresterea energiei.
Într-un experiment se masoara, in general, in mod direct sectiunile eficace topologice, iar prin diferite normari, dependente de experiment, se pot obtine distributiile de multiplicitate.
Descrierea completa a unui proces de interactie necesita informatii asupra distributiilor sectiunilor eficace specifice in termenii energiei sau impulsului oricarui sistem nuclear (particula, nucleu) care exista dupa interactie sau unghiului solid de emisie pentru sistemul nuclear considerat. Astfel de distributii sunt numite sectiuni eficace diferentiale.
Prin aceasta raportare la diferite marimi fizice, sectiunile eficace diferentiale permit obtinerea unui numar mare de caracteristici dinamice ale ciocnirilor nucleare. Fie un proces semiexclusiv de forma:
AP + AT n1a1 + n2a2 + .. + nmam + X , (II.40)
cu ni
(i=1,.,m) numarul de particule de tip ai (i=1,.,m)
detectate in starea finala si X toate celelalte particule produse dar nedetectate. Fie ![]() (i=1,.,m) impulsurile particulelor detectate in starea
finala, exprimate in sistemul centrului de masa (SCM). În
acest caz, sectiunea eficace diferentiala se exprima,
in sistemul centrului de masa, astfel:
(i=1,.,m) impulsurile particulelor detectate in starea
finala, exprimate in sistemul centrului de masa (SCM). În
acest caz, sectiunea eficace diferentiala se exprima,
in sistemul centrului de masa, astfel:
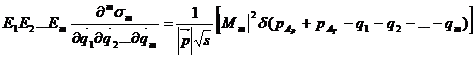 . (II.41)
. (II.41)
În relatia (II.41) Ei (i=1,.,m) sunt energiile particulelor din starea
finala, ![]() este patratul energiei disponibile
in sistemul centrului de masa, Mm
este amplitudinea de ciocnire (reactie), iar
este patratul energiei disponibile
in sistemul centrului de masa, Mm
este amplitudinea de ciocnire (reactie), iar ![]() este impulsul sistemelor nucleare care se
ciocnesc, in sistemul centrului de masa.
este impulsul sistemelor nucleare care se
ciocnesc, in sistemul centrului de masa.
Amplitudinea
de ciocnire depinde de 3m variabile
independente, invariante relativist. Cunoasterea amplitudinii de
ciocnire permite caracterizarea completa a ciocnirii. Pentru amplitudinea
de ciocnire se pot alege variabile diferite: impuls total, impuls longitudinal,
impuls transversal , rapiditate, unghi de emisie, etc. În functie de
variabila in raport cu care se face diferentierea in
relatia (II.41) si de dependenta marimii astfel
obtinute in membrul stang de variabila considerata se
obtin diferite tipuri de distributii. Cele mai importante sunt: distributia unghiulara
(variabila aleasa in acest caz este unghiul de emisie al particulei din starea finala;
notatiile uzuale pentru diferite distributii unghiulare sunt: ![]() ,
, ![]() ,
,![]() ), distributia
de rapiditate (variabila aleasa este rapiditatea, definita prin relatia urmatoare:
), distributia
de rapiditate (variabila aleasa este rapiditatea, definita prin relatia urmatoare: 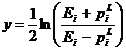 ; o notatie uzuala este:
; o notatie uzuala este: ![]() ) sau distributia
de pseudorapiditate (variabila aleasa este pseudorapiditatea, definita prin relatia
) sau distributia
de pseudorapiditate (variabila aleasa este pseudorapiditatea, definita prin relatia ![]() ; notatia uzuala este:
; notatia uzuala este: ![]() ); distributia de
impuls (notatie uzuala:
); distributia de
impuls (notatie uzuala: ![]() ) si distributia
de energie (notatie uzuala:
) si distributia
de energie (notatie uzuala: ![]() ). Pentru ultimele doua se mai folosesc denumirile de spectrul de impuls, respectiv, spectrul de energie.
). Pentru ultimele doua se mai folosesc denumirile de spectrul de impuls, respectiv, spectrul de energie.
Distributiile considerate anterior permit extragerea unor informatii dinamice extrem de importante pentru descrierea mecanismelor de interactie in ciocniri nucleare relativiste si stabilirea influentei geometriei ciocnirii asupra dinamicii ciocnirii. Cateva din aspectele de interes vor fi discutate in cele ce urmeaza.
Pentru a obtine valoarea experimentala a sectiunii eficace intr‑o ciocnire data trebuie sa fie cunoscute urmatoarele marimi: numarul de interactii in tinta ale nucleului incident si numarul de nuclee incidente pe tinta. Raportul dintre cele doua marimi se inmulteste cu sectiunea eficace pentru ciocnirea nucleon‑nucleon la aceeasi energie, sectiune care este tabelata [53], obtinandu‑se astfel sectiunea eficace a ciocnirii nucleu‑nucleu considerate [3-5,54,55].
Acest mod de determinarea a sectiunilor eficace in ciocniri nucleare relativiste ofera posibilitatea ca rezultatele experimentale obtinute sa prezinte o serie de dependente de interes, cum ar fi:
(i) dependenta de numarul de masa al nucleului tinta;
(ii) dependenta de numarul de masa al nucleului incident;
(iii) dependenta de gradul de centralitate a ciocnirii.
Rezultatele experimentale obtinute in ciocniri nucleu-nucleu la energii peste 1 A GeV indica unele dependente comune, anume [1-5,8-11,54-56]:
(a) sectiunile eficace - atat cele pentru ciocniri centrale, cat si cele pentru ciocniri periferice - cresc cu numarul de masa al nucleului tinta, pentru un nucleu incident dat;
(b) sectiunile eficace pentru ciocniri periferice cresc cu cresterea numarului de masa al nucleului incident, pentru un nucleu tinta dat;
(c) sectiunile eficace pentru ciocniri centrale scad cu cresterea numarului de masa al nucleului incident, pentru un nucleu tinta dat;
(d) pentru o ciocnire data sectiunea eficace scade cu cresterea gradului de centralitate a ciocnirii; scaderea este mult mai rapida pentru sisteme usoare si aproximativ simetrice;
(e) pentru o ciocnire data valoarea sectiunii eficace creste relativ lent cu energia; cresterea sectiunii eficace este mult mai lenta decat cresterea energiei.
Rezultatele
experimentale incluse in Tabelul II.6 si Tabelul II.7, pentru
ciocniri nucleu-nucleu, centrale si periferice, la 4.5 A GeV/c,
confirma aceste dependente. Multe din comportari se pot observa
mai usor folosind rapoarte diferite, cum ar fi: raportul dintre numerele
de masa ale nucleelor care se ciocnesc, raportul dintre sectiunile
eficace ale ciocnirilor considerate la sectiunea eficace pentru ciocnirea
care are suma maxima dintre numerele de masa ale nucleelor care se
ciocnesc sau energia maxima. În Tabelul II.8. sunt incluse
rezultatele obtinute pentru ciocniri O-Pb la energii cuprinse intre
2.1 A GeV si 200 A GeV. Se observa ca raportul ![]() creste mult mai
lent decat raportul dintre energii. Aceasta comportarea ar puea
sugera unele legaturi cu invarianta la scala a sectiunilor
eficace . Invarianta la scala implica gasirea unei variabile,
de obicei data de raportul dintre multiplicitatea dint-un eveniment
si multiplicitatea medie, z=n/<n>, pentru care distributia de
multiplicitate asociata, P(z), nu isi mai schimba forma
sau/si pozitia cu cresterea energiei disponibile in
sistemul centrului de masa, pentru ciocnire data.
creste mult mai
lent decat raportul dintre energii. Aceasta comportarea ar puea
sugera unele legaturi cu invarianta la scala a sectiunilor
eficace . Invarianta la scala implica gasirea unei variabile,
de obicei data de raportul dintre multiplicitatea dint-un eveniment
si multiplicitatea medie, z=n/<n>, pentru care distributia de
multiplicitate asociata, P(z), nu isi mai schimba forma
sau/si pozitia cu cresterea energiei disponibile in
sistemul centrului de masa, pentru ciocnire data.
Din
tipurile de comportari mentionate - pe baza rezultatelor
experimentale incluse in Tabelul II.7 - se mai observa ca
sectiunile eficace centrale isi schimba semnificativ
comportarea - intr-o dependenta de suma razelor nucleelor care se
ciocnesc - pentru ![]() . Aceasta modificare a comportarii se reflecta
si in alte dependente ale sectiunilor eficace. Unele
dintre dependente, cum ar fi cea legata de energia nucleului incident, ar putea sugera unele legaturi
cu proprietatea de invarianta la scala asociata
distributiei de multiplicitate.
. Aceasta modificare a comportarii se reflecta
si in alte dependente ale sectiunilor eficace. Unele
dintre dependente, cum ar fi cea legata de energia nucleului incident, ar putea sugera unele legaturi
cu proprietatea de invarianta la scala asociata
distributiei de multiplicitate.
|
AP - AT |
sexp(mb) |
scalc(mb) |
|
He-Li | ||
|
He-C | ||
|
He-Ne | ||
|
He-Al | ||
|
He-Cu |
| |
|
He-Pb | ||
|
C-Ne | ||
|
C-Si | ||
|
C-Cu | ||
|
C-Zr | ||
|
C-Pb | ||
|
O-Ne | ||
|
O-Pb |
Table II.6. Sectiuni eficace experimentale pentru ciocniri periferice nucleu-nucleu
la 4.5 A GeV/c. Rezultatele calculelor bazate pe relatia (II.42) sunt incluse in tabel
|
AP - AT |
T(qch qn |
sexp(mb) |
|
He-Li |
T(2,0) | |
|
He-Li |
T(5,0) | |
|
He-Li |
T(14,0) | |
|
He-C |
T(2,0) | |
|
He-C |
T(5,0) | |
|
He-C |
T(14,0) | |
|
He-Cu |
T(2,0) | |
|
He-Cu |
T(5,0) | |
|
He-Cu |
T(14,0) | |
|
He-Pb |
T(2,0) | |
|
He-Pb |
T(5,0) | |
|
He-Pb |
T(14,0) | |
|
C-C |
T(2,0) | |
|
C-C |
T(5,0) | |
|
C-C |
T(14,0) | |
|
C-Ne |
T(2,0) | |
|
C-Ne |
T(5,0) | |
|
C-Ne |
T(14,0) | |
|
C-Cu |
T(2,0) | |
|
C-Cu |
T(5,0) | |
|
C-Cu |
T(14,0) | |
|
C-Zr |
T(2,0) | |
|
C-Zr |
T(5,0) | |
|
C-Zr |
T(14,0) | |
|
C-Pb |
T(2,0) | |
|
C-Pb |
T(5,0) | |
|
C-Pb |
T(14,0) | |
|
O-Ne |
T(2,0) | |
|
O-Ne |
T(5,0) | |
|
O-Ne |
T(14,0) | |
|
O-Pb |
T(2,0) | |
|
O-Pb |
T(5,0) | |
|
O-Pb |
T(14,0) |
Tabelul II.7. Sectiuni eficace experimentale pentru ciocnri centrale
nucleu-nucleu la 4.5 A GeV/c
|
E (GeV/A) |
sexp(mb) |
sexp(E/A) / sexp(200 GeV/A) |
Tabelul II.8. Compararea sectiunilor eficace experimentale obtinute in ciocniri
periferice (inelastice) O-Pb la diferite energii relativiste
Dependentele experimentale observate sugereaza o descriere pe baza unor relatii geometrice. Pentru ciocnirile periferice (inelastice) se pot folosi relatii de forma [4,5,20,54-56]:
![]() , (II.42)
, (II.42)
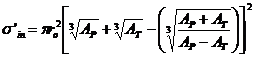 . (II.43)
. (II.43)
Dependenta
data de relatia (II.42) sugereaza ca nucleele care se
ciocnesc la energii mari interactioneaza in mod eficient
intr‑o distanta ![]() . În aceasta relatii d este un parametru de corectie care este datorat
'moliciunii' (transparentei) nivelelor cu nucleoni de la
suprafata nucleelor. Aceasta "moliciune" este o consecinta
a proprietatii de saturatie a fortelor nucleare [57,58].
. În aceasta relatii d este un parametru de corectie care este datorat
'moliciunii' (transparentei) nivelelor cu nucleoni de la
suprafata nucleelor. Aceasta "moliciune" este o consecinta
a proprietatii de saturatie a fortelor nucleare [57,58].
Valorile parametrilor ro si d variaza de la experiment la experiment. Astfel, in lucrarea [54] valorile considerate sunt ro = 1.3 Fm si d = 0.6, iar in lucrarea [56] se raporteaza valorile ro = 1.2 Fm si d = 1.3. Din fit‑urile la rezultatele experimentale obtinute in unele ciocniri nucleu-nucleu la 4.5 A GeV/c facute pana in prezent s‑au obtinut urmatoarele valori ale celor doi parametri: ro = 1.25 Fm, d
Relatia (II.43) sugereaza o modelare fenomenologica geometrica a tuturor ciocnirilor nucleu‑nucleu la energii peste 1 A GeV. Ea va fi discutata in cadrul partii a treia a cursului, consacrata modelarii dinamicii ciocnirilor nucleare relativiste. Ca si relatia (II.42), relatia (II.43) este utila pentru sectiunile eficace inelastice. Ea se poate aplica numai pentru ciocniri nesimetrice, insa. Cea mai folosita valoare a parametrului ro este, in acest caz, 1.4 Fm [3-5,55].
Este important de subliniat aici faptul ca relatiile (II.42) si (II.43) pot fi folosite si pentru sublinierea influentei geometriei ciocnirii asupra dinamicii ciocnirii pe un domeniu foarte larg de energii (1-200 A GeV) [3-5,8,9,30,31,54-56,59]. Ele pot fi legate, de asemenea, de diferite marimi fizice de interes pentru a aflat informatii noi asupra dinamicii ciocnirii. Printre aceste marimi se numara multiplicitatea, numarul de participanti, interferometria de intensitate etc. Unele dintre aceste conexiuni au fost deja amintite, iar altele se vor prezenta in capitolele urmatoare.
Trebuie mentionat - in incheierea acestei prezentari - faptul ca metoda de determinare experimentala a sectiunii eficace in ciocniri nucleare relativiste este afectata de cateva surse de eroare. Aceste surse de eroare sunt legate, in general, de caracteristicile tehnice ale sistemului de detectie si de metoda de prelucrare a datelor experimentale primare. Pentru Spectrometrul SKM 200 de la IUCN Dubna, sistem de detectie cu ajutorul caruia s-au obtinut majoritatea datelor experimentale folosite la laboratorul asociat cursului de Fizica nucleara relativista sursele de eroare legate de caracteristicile tehnice ale sistemului de detectie sunt determinate de timpii morti ai detectorilor cu scintilatie montati in anticoincidenta (tm = 20 ns), precum si de posibilitatea unor declansari incorecte, mai ales pentru ciocniri centrale, de catre un fragment al nucleului incident. Corectiile necesare la sectiunea eficace sunt de 2‑4 %, in primul caz, respectiv, 1‑2 %, in cel de al doilea caz.
Principalele surse de eroare determinate de metoda de explorare sunt ineficacitatea de explorare si pierderile de la explorare. Primele impun corectii in jur de 1 %, iar celelalte necesita corectii intre 1 % si 3 %, in functie de numarul de masa al nucleului tinta. Exista si alte surse de eroare, dar acestea impun corectii foarte mici asupra valorii experimentale a sectiunii eficace [4,20,54,55].
|
Politica de confidentialitate |
| Copyright ©
2024 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |