Vectori
Marimile fizice sunt de trei tipuri: scalare, vectoriale si tensoriale.
Marimile vectoriale sunt definite prin: valoare numerica (modul), punct de aplicatie, directie (suport) si sens. Vectorii sunt reprezentati sub forma unor segmente de dreapta orientate, clasificandu-se in vectori legati, vectori alunecatori si vectori liberi. Vectorii legati sau ficsi sunt determinati prin toate elementele mentionate: modul, punct de aplicatie, directie si sens; ex: viteza si acceleratia punctului material. Vectorii alunecatori sunt definiti prin directie, sens si modul, iar punctul de aplicatie se poate deplasa pe suport; ex: fortele aplicate corpului solid rigid. Vectorii liberi sunt determinati prin directie, sens si modul, iar punctul de aplicatie se poate deplasa in orice punct din spatiu; ex: momentul cuplului de forte.
Egalitatea vectorilor. Vectorii care reprezinta marimi de aceeasi natura sunt egali cand sunt definiti prin aceleasi elemente. Vectorii care au aceeasi marime, sens si directie sunt echipolenti.
Adunarea vectorilor. Pentru vectorii
liberi ![]() si
si ![]() (Fig. 1.3.a) vectorul
suma
(Fig. 1.3.a) vectorul
suma ![]()
![]() se determina cu regula paralelogramului: in originea O a vectorului
se determina cu regula paralelogramului: in originea O a vectorului ![]() se construieste
un vector echipolent cu
se construieste
un vector echipolent cu ![]() ; vectorul suma
; vectorul suma ![]() (numit si vector
rezultant sau rezultanta vectorilor
(numit si vector
rezultant sau rezultanta vectorilor ![]() si
si ![]() ) este diagonala paralelogramului construit pe vectorii
) este diagonala paralelogramului construit pe vectorii ![]() si
si ![]() (Fig. 1.3.b), avand
originea in O. Marimea
vectorului
(Fig. 1.3.b), avand
originea in O. Marimea
vectorului ![]() poate fi
calculata cu teorema lui Pitagora generalizata:
poate fi
calculata cu teorema lui Pitagora generalizata:
![]()
Vectorul suma al vectorilor liberi ![]() si
si ![]() mai poate fi
determinat cu regula triunghiului:
desenand in varful lui
mai poate fi
determinat cu regula triunghiului:
desenand in varful lui ![]() un vector echipolent
cu
un vector echipolent
cu ![]() , vectorul
, vectorul ![]() inchide triunghiul
astfel format, avand originea in O
si varful in varful lui
inchide triunghiul
astfel format, avand originea in O
si varful in varful lui ![]() , iar sensul de la originea lui
, iar sensul de la originea lui ![]() spre varful lui
spre varful lui ![]() (Fig. 1.3.c).
(Fig. 1.3.c).
Se observa ca prin schimbarea
ordinei de insumare nu se modifica rezultatul, deci adunarea vectorilor
este comutativa: ![]() . Adunarea vectorilor este si o operatie asociativa,
astfel ca, pentru trei vectori
. Adunarea vectorilor este si o operatie asociativa,
astfel ca, pentru trei vectori ![]() ,
, ![]() si
si ![]() , vectorul rezultant poate fi calculat fie prin insumarea
celui de-al treilea cu suma primilor doi (Fig. 1.3.d), fie prin insumarea celui
dintai cu suma ultimilor doi (Fig. 1.3.e), ceea ce se scrie:
, vectorul rezultant poate fi calculat fie prin insumarea
celui de-al treilea cu suma primilor doi (Fig. 1.3.d), fie prin insumarea celui
dintai cu suma ultimilor doi (Fig. 1.3.e), ceea ce se scrie: ![]() .
.
Adunarea
mai multor vectori se poate face prin generalizarea regulii triunghiului,
stabilindu-se regula conturului poligonal.
Aceasta consta in construirea unui contur poligonal prin asezarea
succesiva a vectorilor echipolenti termenilor adunarii, cu
originile in varfurilor vectorilor precedenti. Vectorul suma inchide
conturul poligonului astfel construit si are originea comuna cu a
primului vector: ![]() (Fig. 1.3.f).
(Fig. 1.3.f).
|
a |
0
b. |
0
c. |
||||||||
|
( d. |
0 e. |
f. |
Fig. 1.3. Adunarea vectorilor
Scaderea
vectorilor se efectueaza prin intermediul
adunarii. Pentru doi vectori liberi ![]() si
si ![]() , vectorul diferenta se poate scrie
, vectorul diferenta se poate scrie ![]() . Astfel, vectorul
. Astfel, vectorul ![]() devine suma vectorilor
devine suma vectorilor
![]() si -
si - ![]() (Fig. 1.4).
(Fig. 1.4).
|
|
0 |
Fig. 1.4. Scaderea vectorilor
Inmultirea
unui vector cu un scalar. Daca α este un
scalar, atunci produsul α![]() este un vector a carui marime este egala cu
produsul dintre α si valoarea absoluta a vectorului
este un vector a carui marime este egala cu
produsul dintre α si valoarea absoluta a vectorului ![]() . Vectorul α
. Vectorul α![]() are acelasi sens cu vectorul
are acelasi sens cu vectorul ![]() daca α este
pozitiv, iar sensul este opus daca α este negativ.
daca α este
pozitiv, iar sensul este opus daca α este negativ.
Produsul scalar a doi vectori ![]() si
si ![]() este rezultatul inmultirii modulelor acestora si a
cosinusul unghiului format de directiile lor:
este rezultatul inmultirii modulelor acestora si a
cosinusul unghiului format de directiile lor:
![]()
Produsul scalar este comutativ: ![]() si distributiv
fata de adunarea vectorilor:
si distributiv
fata de adunarea vectorilor: ![]() . Pentru vectorii paraleli de aceleasi sens: cos
. Pentru vectorii paraleli de aceleasi sens: cos![]() =1, deci
=1, deci ![]() ; pentru vectorii paraleli cu sensuri contrare cos
; pentru vectorii paraleli cu sensuri contrare cos![]() = -1, deci
= -1, deci ![]() ; produsul scalar a doi vectori perpendiculari este nul
deoarece cos
; produsul scalar a doi vectori perpendiculari este nul
deoarece cos![]() =0.
=0.
Produsul vectorial a doi vectori ![]() si
si ![]() este un vector notat
este un vector notat ![]() . Marimea produsului vectorial este egala cu aria
suprafetei plane definita de cei doi vectori:
. Marimea produsului vectorial este egala cu aria
suprafetei plane definita de cei doi vectori: ![]() (Fig. 1.5). Vectorul
(Fig. 1.5). Vectorul ![]() are originea in punctul
de concurenta a celor doi vectori
are originea in punctul
de concurenta a celor doi vectori ![]() si
si ![]() , directia perpendiculara pe planul format de
acestia si sensul stabilit cu regula burghiului
sau regula mainii drepte .
, directia perpendiculara pe planul format de
acestia si sensul stabilit cu regula burghiului
sau regula mainii drepte .
Produsul
vectorial nu este comutativ: ![]() , dar este distributiv fata de adunarea vectorilor:
, dar este distributiv fata de adunarea vectorilor:
![]() .
.
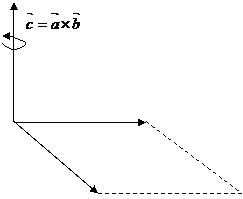
![]()
![]()
![]()
![]()
Fig.1.5. Produsul vectorial
Versorii si componentele
ortogonale ale unui vector. Versorul directiei
unui vector ![]() este un vector
este un vector ![]() , unde a
(scrisa si
, unde a
(scrisa si ![]() ) este marimea vectorului
) este marimea vectorului ![]() . Acesta este adimensional, are marimea egala cu
unitatea si are aceeasi directie cu vectorul
. Acesta este adimensional, are marimea egala cu
unitatea si are aceeasi directie cu vectorul ![]() .
.
Considerand ca originea vectorului
![]() coincide cu originea
unui sistem de axe triortogonal drept
(cartezian) Oxyz, pentru care
versorii acestor axe sunt
coincide cu originea
unui sistem de axe triortogonal drept
(cartezian) Oxyz, pentru care
versorii acestor axe sunt ![]() ,
, ![]() ,
, ![]() , regula paralelogramului permite descompunerea
vectorului
, regula paralelogramului permite descompunerea
vectorului ![]() in trei componente
reciproc ortogonale, scrise
in trei componente
reciproc ortogonale, scrise ![]() ,
, ![]() ,
, ![]() , astfel incat:
, astfel incat:
![]() .
.
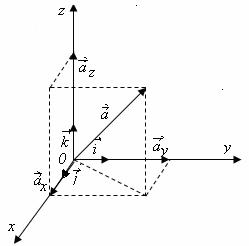
Fig. 1.6. Componentele ortogonale ale unui vector in sistemul cartezian Oxyz
Pentru un vector de pozitie ![]() al unui punct material
cu coordonatele x, y, z, relatia anterioara
devine:
al unui punct material
cu coordonatele x, y, z, relatia anterioara
devine:
![]()
Proiectiile
vectorului ![]() pe axele Ox, Oy
si Oz, marimile scalare
pe axele Ox, Oy
si Oz, marimile scalare ![]() ,
, ![]() ,
, ![]() , pot fi scrise in functie de unghiurile α, β,
γ, pe care le face vectorul
, pot fi scrise in functie de unghiurile α, β,
γ, pe care le face vectorul ![]() cu fiecare dintre
aceste axe, astfel:
cu fiecare dintre
aceste axe, astfel:
![]() ,
, ![]() ,
, ![]() .
.
Aceste
cosinusuri sunt numite cosinusurile directoare ale vectorului ![]() , iar intre ele exista relatia:
, iar intre ele exista relatia:
![]() .
.
Marimea vectorului ![]() este data de expresia:
este data de expresia:
![]() (Fig. 1.6).
(Fig. 1.6).
Intr-un
sistem de coordonate sferice polare (r, θ, φ), marimile ![]() ,
, ![]() ,
, ![]() se pot scrie
astfel:
se pot scrie
astfel:
![]()
![]()
![]()
unde θ reprezinta unghiul azimut, 0 ≤ θ < 2π, iar φ unghiul polar, 0 ≤ φ ≤ π (Fig. 1.7).
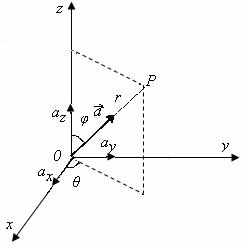
Fig. 1.7. Componentele ortogonale ale unui vector in sistemul de coordonate sferice (r, θ, φ)
Diferentiala unui vector. In analiza matematica, diferentiala descrie o schimbare
infinitezimala a unei variabile. In fizica, variatia unei
marimi ![]() este notata in
general cu
este notata in
general cu ![]() , sau, atunci cand aceasta variatie tinde spre
infinitul mic, cu
, sau, atunci cand aceasta variatie tinde spre
infinitul mic, cu ![]() .
.
Daca marimea ![]() depinde de o
singura variabila, t,
diferentiala sa este:
depinde de o
singura variabila, t,
diferentiala sa este: ![]() .
.
Daca
marimea ![]() depinde de variabilele
x, y, z, atunci diferentiala sa se scrie:
depinde de variabilele
x, y, z, atunci diferentiala sa se scrie:
![]() .
.
Pentru un
vector de pozitie ![]() ,
, ![]() ,
, ![]() ,
, ![]() , deci:
, deci: ![]() .
.
Derivata
unui vector. Daca un vector ![]() depinde de un
parametru oarecare
depinde de un
parametru oarecare![]() , derivata vectorului
, derivata vectorului ![]() in functie de
in functie de ![]() este:
este:
![]() ,
,
iar pentru doi
vectori variabili ![]() si
si ![]() , functii de parametrul
, functii de parametrul ![]() :
:
![]() .
.
Derivata produsului
dintre un scalar ![]() si un vector
si un vector ![]() , functii de acelasi parametru
, functii de acelasi parametru ![]() , este:
, este: ![]() .
.
Derivata produsului scalar:
![]() .
.
Derivata produsului vectorial:
![]() .
.
Integrala unui vector. Daca pentru un camp vectorial caracterizat prin marimea ![]() se poate scrie
integrala curbilinie
se poate scrie
integrala curbilinie ![]() , exprimand vectorul
, exprimand vectorul ![]() in functie de
componentele sale ortogonale astfel:
in functie de
componentele sale ortogonale astfel:
![]() ,
,
si avand in vedere
relatia ![]() , se obtine:
, se obtine:
![]() .
.
Operatori. Gradientul se aplica
unei marimi scalare ![]() iar rezultatul este un
vector:
iar rezultatul este un
vector:
![]() .
.
Divergenta de aplica unui vector si rezultatul este o marime scalara:
div ![]() .
.
Rotorul se aplica unui vector si rezultatul este un vector:
rot 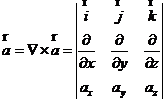 .
.
|
Politica de confidentialitate |
| Copyright ©
2024 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |