Algoritmul Bellman-Ford

Algoritmul Bellman-Ford

Acest algoritm gaseste cele mai scurte cai de la toate nodurile unui graf orientat pana la un anumit nod destinatie.

Observatie: Problema gasirii celor mai scurte cai de la un nod destinatie dat pana la toate celelalte noduri ale grafului este echivalenta cu cea a gasirii celor mai scurte cai de la toate nodurile pana la nodul destinatie: o problema se obtine din cealalta prin schimbarea sensului fiecarui arc (pastrand insa ponderea sa).

Pentru simplificarea prezentarii - dar fara a afecta gradul de generalitate al algoritmului -, sa presupunem ca nodul 1 reprezinta nodul destinatie. Atunci, problema consta in a gasi calea cea mai scurta de la fiecare nod la nodul

  Vom nota cu d_ij ponderea arcului ( i , j ) - numita si lungimea arcului sau distanta dintre nodul i si nodul j -, cu conventia

daca intre nodul i si nodul j nu exista un arc cu sensul de la primul la al doilea nod. Utilizand aceasta conventie, se poate face ipoteza - care nu impieteaza asupra gradului de generalitate - ca exista un arc intre oricare pereche de noduri, intrucat traseele si caile formate din arcele reale ale grafului vor fi singurele cu o lungime finita

Cea mai scurta cale de la un nod dat i la nodul 1 si care indeplineste conditiile de a contine cel mult h arce si de a trece prin nodul 1 doar o singura data se numeste o cea mai scurta cale ( h) de la nodul i la nodul 1 iar lungimea ei se noteaza cu .

Observatie: O astfel de cale s-ar putea sa treaca de mai multe ori prin acelasi nod deci sa nu constituie un traseu. Vom prezenta mai departe conditiile ca sa nu se intample asa ceva.

Algoritmul Bellman-Ford: Intr-un graf cu N noduri, sub conventiile (1) si

  ,

cele mai scurte trasee ( h) sunt date de iteratiile

 

pornind cu conditiile initiale

.

  Algoritmul se termina dupa un numar finit de iteratii

h  N

numai si numai daca toate buclele care nu contin nodul 1 au o lungime ne-negativa si, la final, reprezinta lungimea celei mai scurte cai, adica

  .

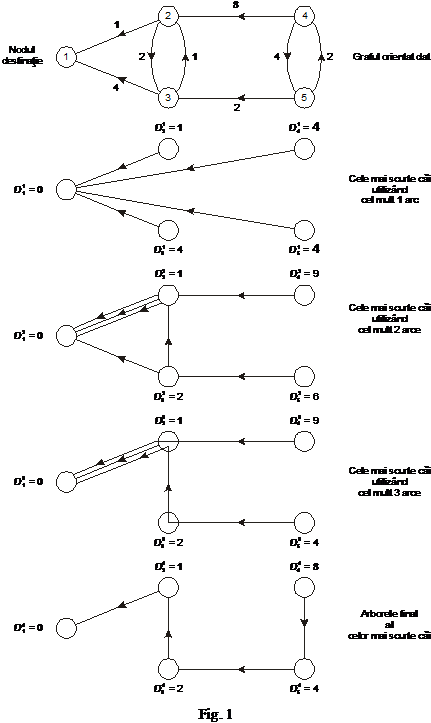
Acest algoritm gaseste mai intai traseele cele mai scurte de un arc, apoi traseele cele mai scurte de doua arce si asa mai departe. Un exemplu este ilustrat in
fig. 1, pentru un graf cu N = 5 noduri si in care cele mai scurte trasee ( h) constituie cai intrucat toate lungimile arcelor sunt pozitive si, deci, toate buclele au o lungime pozitiva

Pentru a demonstra ca scalarii generati conform algortimului reprezinta traseele cele mai scurte ( h) vom folosi metoda inductiei. Din (2)₂ si (2)₃ obtinem

 

astfel incat este, intr-adevar, egal cu lungimea traseului cel mai scurt ( 1) de la i la 1. Sa presupunem ca este egal cu lungimea traseului cel mai scurt ( k) de la i la 1 pentru k  h. Sa dovedim ca reprezinta lungimea traseului cel mai scurt ( h + 1) de la i la 1. Intr-adevar, un cel mai scurt drum ( h + 1) de la i la 1 fie este format din mai putin de h + 1 arce, caz in care lungimea sa este egala cu , fie consta din h + 1 arce, in care caz primul arc este (i , j) pentru un oarecare j  1, urmat de un traseu format din h arce de la j la 1 si in care nodul 1 nu apare repetat. Ultimul traseu trebuie sa fie un cel mai scurt traseu ( h) de la j la 1, caci, in caz contrar, prin concatenarea arcului (i , j) cu un traseu mai scurt ( h) de la j la 1 am obtine un traseu mai scurt ( h + 1) de la j la 1. Asadar

  lungimea traseului cel mai scurt ( h + 1) = .

Folosind metoda inductiei, vom avea

 

intrucat multimea de trasee ( k) de la nodul j la nodul 1 contine multimea corespondenta de trasee ( k - 1)). Prin urmare

  .

In plus, avem

  ,

astfel incat - din (6) - obtinem

lungimea traseului cel mai scurt ( h + 1) =

  = .

Cum (conform (8)),

  ,

din (10) rezulta

  lungimea traseului cel mai scurt ( h + 1) = .

q.e.d. 

Sa dovedim acum ca algoritmul Bellman-Ford se termina in cel mult N iteratii. Din relatia (4) se deduce ca nu putem reduce lungimile celor mai scurte tresee permitand un numar tot mai mare de arce in componenta traseelor. Rezulta ca nu poate exista un ciclu cu lungime negativa care sa nu contina nodul 1, intrucat un astfel de ciclu ar putea fi parcurs, in mod repetat, de un numar arbitrar de mare de ori in traseele de la un nod oarecare la nodul 1, facand, prin urmare, ca lungimea lor sa devina arbitrar de mica deci contrazicand relatia (4). Reciproc, sa presupunem ca toate ciclurile care nu contin nodul 1 au o lungime ne-negativa. Atunci, prin eliminarea tuturor astfel de cicluri din cele mai scurte trasee ( h), vom obtine cai de aceeasi lungime sau mai mica. Prin urmare, pentru fiecare i si fiecare h, va exista o cale care sa reprezinte cel mai scurt traseu ( h) de la i la 1 iar lungimea corespunzatoare a caii celei mai scurte va fi egala cu . Cum caile nu contin cicluri, ele pot fi constituite din cel mult N - 1 arce. Rezulta ca

  ,

ceea ce denota ca algoritmul se termina dupa cel mult N iteratii.  q.e.d. 

Observatie: Rezultatul obtinut ramane valabil chiar daca nu exista, in graful originar, nici o cale de la anumite noduri i la nodul 1. La terminarea algoritmului, vom avea, pentru acele noduri, .

Pentru a estima volumul de calcul necesar pentru gasirea lungimilor celor mai scurte cai, vom observa ca, in cel mai defavorabil caz, algoritmul necesita N iteratii, fiecare iteratie trebuie efectuata pentru N - 1 noduri iar, pentru fiecare nod, minimizarea se face intre cel mult N - 1 alternative. Asadar, volumul de calcul necesar creste, in cel mai defavorabil caz, proportional cu N ³ - ceea ce se mai scrie si sub forma O (N ³) . In fond, o analiza mai atenta evidentiaza faptul ca volumul de calcul este O (mA), unde A reprezinta numarul de arce iar m este numarul necesar de iteratii pana la terminare (fiind, de asemenea, numarul maxim de arce continute de calea cea mai scurta

Exemplu Graful din fig. A prezinta efectul unui ciclu de lungime negativa care nu contine nodul 1 si ilustreaza faptul ca se poate testa existenta unui astfel de ciclu prin simpla comparare a lui cu pentru fiecare i. Intr-adevar, conform conditiei de terminare a algoritmului Bellman-Ford, exista un astfel de ciclu de lungime negativa daca si numai daca (vezi (4)*) pentru un i oarecare. Lungimea celei mai scurte cai de la nodul 2 la nodul 1 din graf este egala cu 1. Algoritmul Bellman-Ford da si , indicand existenta unui ciclu de lungime negativa.

Pentru constructia celei mai scurte cai, sa presupunem ca toate ciclurile care nu contin nodul 1 au o lungime ne-negativa si sa notam cu D_i lungimea celei mai scurte cai de la nodul i la nodul 1. La terminarea algoritmului Bellman-Ford, vom obtine (ecuatia Bellman-Ford

   

care se traduce astfel: lungimea celei mai scurte cai de la nodul i la nodul 1 este data de suma dintre lungimea arcului care duce la nodul urmator dupa i pe calea cea mai scurta si lungimea celei mai scurte cai de la acel nod la nodul 1

Ecuatia Bellman-Ford permite gasirea cu usurinta a celor mai scurte cai (si nu a lungimilor celor mai scurte cai) daca toate ciclurile care nu contin nodul 1 au o lungime pozitiva (si nu o lungime zero). In acest scop, vom selecta, pentru fiecare i  1, un nod vecin j pentru care arcul (i , j) atinge un minim in relatia (13)₁ si vom considera subgraful format din aceste N - 1 arce (un exemplu ilustrativ este dat in fig. 2).

Pentru a gasi cea mai scurta cale din oricare nod i, vom porni din nodul i si vom urma arcele corespunzatoare ale subgrafului pana ajungem in nodul 1

Observatie: Un acelasi nod nu poate fi strabatut de doua ori inainte de a ajunge la nodul 1, intrucat, in caz contrar, s-ar forma un ciclu care - in virtutea relatiei (13)₁ - ar avea o lungime egala cu zero. Intr-adevar, fie, spre exemplu, (i₁ , i₂ , . , i_k , i₁) un astfel de ciclu; daca insumam ecuatiile

vom obtine

.

Intrucat subgraful obtinut conecteaza fiecare nod cu nodul 1 si are N - 1 arce, el trebuie sa fie un arbore acoperitor. Vom numi acest subgraf arborele acoperitor cu cele mai scurte cai [shortest path spanning tree], observand ca el are o structura speciala si anume: nodul 1 reprezinta radacina iar fiecare arc al arborelui este orientat catre radacina

In [Bert ] se arata cum poate fi obtinut arborele acoperitor cu cele mai scurte cai in cazul cand exista cicluri de lungime zero.

Utilizand constructia prezentata mai sus, se poate dovedi urmatoarea

Teorema Daca nu exista cicluri de lungime zero sau negativa, atunci ecuatia Bellman (vazuta ca un sistem de N ecuatii cu N necunoscute) are o solutie unica.

Demonstratie: Sa presupunem ca sunt alte solutii ale ecuatiei Bellman (13)₁ cu . Vom dovedi ca sunt egale cu lungimile D_i ale celor mai scurte cai. Sa reutilizam constructia cailor prezentata mai sus inlocuind D_i cu . Atunci va fi lungimea caii corespunzatoare de la nodul i la nodul1 cu . Sa consideram algoritmul Bellman-Ford cu doua conditii initiale diferite. Prima conditie initiala este pentru i  1 si , in care caz adevaratele lungimi D_i ale celor mai scurte cai se obtin dupa cel mult N - 1 iteratii. Cea de a doua conditie initiala este , in care caz se obtine dupa fiecare iteratie intrucat sunt solutii ale ecuatiei Bellman). Intrucat cea de a doua conditie initiala este - pentru fiecare i - mai mica decat sau cel mult egala cu prima conditie initiala, rezulta din iteratia Bellman-Ford (2)₂ ca . Prin urmare si unica solutie a ecuatiei Bellman o constituie multimea de adevarate lungimi D_i ale celor mai scurte cai q.e.d. 

In [Bert ] se demonstreaza ca, daca exista cicluri de lungime zero care nu cuprind nodul 1, atunci ecuatia Bellman nu are o solutie unica (desi algoritmul Bellman-Ford tot se termina cu lungimile corecte ale celor mai scurte cai daca se pleaca din conditiile initiale (2)₃ .

Algoritmul Belmann-Ford are proprietatea ca lucreaza corect chiar in situatia cand conditiile initiale pentru i  1 sunt numere arbitrare si cand iteratiile sunt efectuate in paralel pentru diferite noduri, in practic oricare ordine.

In continuare vom prezenta o versiune distribuita, asincrona a algoritmului Bellman-Ford - similara celei utilizate, inca din 1969, in reteaua ARPANET (unde fiecare pachet este dirijat independent de celelalte pachete din aceeasi sesiune) dar si destul de apropiata de metoda de dirijare din reteaua DNA - care calculeaza cele mai scurte distante de la fiecare nod sursa la oricare nod destinatie si care face fata modificarilor in timp ale lungimilor cailor (fie din cauza defectarii si reparatiilor unor linii, fie din cauza modificarilor de trafic din retea). Un aspect interesant al acestui algoritm il constituie faptul ca el necesita stocarea la noduri a unor informatii reduse - doar privind lungimile liniilor divergente din nod si identitatea oricarei destinatii si nu despre intreaga topologie a retelei).

Vom presupune ca fiecare ciclu are o lungime pozitiva, ca reteaua poseda, in orice moment, un grad de conectivitate mare si ca, daca (i , j) constituie o legatura, atunci si (j , i) reprezinta o legatura. Vom avea in vedere situatia (care corespunde realitatii practice) cand lungimile d_ij sufera variatii in timp. In analiza ce urmeaza vom presupune, totusi, ca lungimile d_ij sunt fixe dar ca conditiile initiale pot fi arbitrare. Aceste ipoteze furnizeaza un model adecvat pentru situatia cand lungimile legaturilor raman fixe dupa un anumit interval de timp t₀ de la o serie de schimbari.

Ne vom ocupa de cea mai mica distanta D_i de la fiecare nod i la un nod destinatie generic - fie el nodul 1, pentru a avea o situatie concreta in realitate, pentru fiecare nod destinatie trebuie executata o versiune separata a algoritmului). In ipotezele facute, aceste distante constituie solutia unica a ecuatiei Bellman (13) cu

j  N (i)

unde N (i) denota multimea vecinilor curenti ai nodului i (adica a nodurilor conectate cu i printr-o legatura cu sensul catre acesta).

Algoritmul Bellman-Ford va avea forma

 

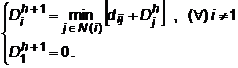
Am vazut ca algoritmul este convergent si conduce corect la cele mai scurte distante pentru conditiile initiale (2)₃ si

.

Algoritmul este propice pentru calculare distribuita intrucat iteratiile Bellman-Ford (2)^*₂ pot fi executate la fiecare nod i in paralel cu oricare alt nod. O posibilitate ar fi ca toate nodurile i sa efectueze iteratiile simultan, sa faca schimb de rezultate ale calculelor cu vecinii lor si sa execute din nou iteratiile cu indicele h incrementat cu o unitate. Cand se aplica conditiile initiale (2)₃ si (2)^*₁ , algoritmul se va termina dupa cel mult N iteratii (unde N este numarul de noduri ale grafului), fiecare nod i afland atat cea mai scurta distanta D_i cat si arcul (legatura) de iesire pe cea mai scurta cale spre nodul 1.

Din pacate, implementarea algoritmului intr-o astfel de maniera sincrona nu este atat de usoara pe cat pare, aparand o dubla dificultate: in primul rand, este necesar un mecanism pentru a face ca toate nodurile sa cada de acord pentru a declansa algoritmul; in al doilea rand, este necesar un mecanism pentru a iesi din algoritm si a porni o noua versiune daca starea sau lungimea unei legaturi se modifica in timpul derularii algoritmului. Desi este posibila rezolvarea cu succes a acestor dificultati [Sega ], algoritmul devine mult mai complex si, deci, mai impropriu de implementat.

O alternativa mai simpla o constituie o versiune asincrona a algoritmului Bellman-Ford, alternativa care nu cere neaparat mentinerea sincronismului intre noduri si care permite inceperea iteratiilor cu conditiile initiale (2)₃ si (2)^*₁ . Aceasta elimina necesitatea unui protocol de initializare sau de repornire a algoritmului. Algoritmul functioneaza la nesfarsit, executand, din timp in timp, la fiecare nod i  1, iteratia

 

utilizand ultimele estimari D_j primite din partea vecinilor j  N (i) si cele mai recente informatii despre starea si lungimea legaturilor care ies din respectivul nod i. Algoritmul mai cere ca fiecare nod i sa transmita, din timp in timp, ultimele sale estimari ale D_i catre toti vecinii sai. Dar nu este necesara sincronizarea, la toate nodurile, nici a iteratiilor, nici a transmisiilor de mesaje. In plus, nu se face nici o presupunere asupra valorilor initiale ale D_j , j  N (i) disponibile la fiecare nod i. Singura cerinta este ca un nod i sa execute in final iteratia Bellman-Ford (13)^*₁ si sa transmita, in cele din urma, rezultatul catre vecini - ceea ce inseamna un mod de functionare total asincron.

Algoritmul ramane corect si cand este executat in mod asincron. Pentru a dovedi acest lucru vom demonstra ca, daca un numar de legaturi isi modifica lungimea pana la un anumit moment t₀ dar nu si ulterior, algoritmul asincron gaseste corect, intr-un interval de timp finit dupa t₀ , cele mai scurte distante de la fiecare nod i (precizam ca, acest algoritm a fost implementat in versiunea originara a retelei ARPANET , cu schimburi de informatii, la fiecare 625 [ms], intre nodurile vecine priivitor la valorile curent estimate D_j ale celor mai scurte distante dar fara repornirea algoritmului dupa modificarea lungimii unei legaturi sau defectarea acesteia - deoarece lungimile d_ij ale legaturilor se modificau foarte des in aceasta retea, conditia de atingere a unui regim stationar, presupusa de functionarea corecta a algoritmului expus aici, fiind arareori obtinuta

Algoritmul Bellman-Ford distribuit, asincron: In fiecare moment t, un nod i (i  1) dispune de:

m      estimata a celei mai scurte distante pana la fiecare din nodurile vecine j (j  N (i)) cu care a comunicat ultima data nodul i ;

m      Estimata D_i (t) a celei mai scurte distante de la nodul i care a fost ultima data calculata in acest nod conform iteratiilor Bellman-Ford

Estimatele distantelor pana la nodul destinatie 1 sunt, prin definitie, zero, adica

 

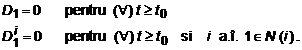
  Fiecare nod i dispune de lungimile d_ij (j  N (i)) ale tuturor legaturilor cu vecinii, lungimi care sunt presupuse constante dupa momentul initial t₀ . Se presupune ca estimatele distantelor nu se modifica, cu exceptia unor anumite momente t₀ , t₁ , t₂ , . (unde

t_m > t_m

  cu

cand, la fiecare nod i (i  1) are loc unul din urmatoarele trei evenimente:

Nodul i actualizeaza valoarea lui D_i (t) conform iteratiei

 

si lasa neschimbate estimatele .

Nodul i primeste, de la unul sau mai multi vecini j  N (i), valoarea lui D_j care a fost calculata in nodul j la un oarecare moment anterior, actualizeaza estimata si lasa neschimbate toate celelalte estimate.

Nodul i este inactiv, caz in care toate estimatele disponibile in acest nod sunt lasate neschimbate.

Fie T ⁱ multimea momentelor la care apare o actualizare ca in cazul 1 la nodul 1 si multimea momentelor la care se primeste la nodul i un mesaj de la nodul j, ca in cazul 2.

Se fac urmatoarele ipoteze:

Nodurile nu inceteaza nici o data sa si actualizeze estimatele si sa primeasca mesaje de la toti vecinii (adica T ⁱ si au un numar infinit de elemente pentru toti i  1 si j  N (i) ).

Informatiile despre vechile distante sunt, in final, purjate din sistem (adica, dandu-se oricare moment de timp , exista un moment astfel incat estimatele D_j , calculate la nodul j anterior momentului , nu sunt receptionate la nici un nod vecin i dupa momentul ).

In ipotezele de mai sus si presupunand ca oricare ciclu are o lungime pozitiva, fie conditiile initiale D_i (t₀) si , , niste numere arbitrare. Atunci exista un moment t_m astfel incat

  D_i (t) , () t  t_m , i =

unde D_i reprezinta valoarea corecta a celei mai scurte distante de la nodul i pana la nodul destinatie 1 (adica estimatele converg c tre valoarea corecta intr-un timp finit).

Observatie: Algoritmul functioneaza corect daca exista o cale de la fiecare nod pana la nodul 1. In caz contrar, algoritmul se aplica sub-grafului care este conex cu nodul 1. Pentru un nod i care apartine unui sub-graf caruia nodul i nu-i apartine dar are cel putin un vecin (astfel incat sa fie capabil sa execute algoritmul), se va obtine pentru . Aceasta proprietate poate fi utilizata de catre un nod pentru a identifica destinatia cu care nu este conectat.

Algoritmul Bellman-Ford distribuit, asincron prezinta doua dezavantaje:

In cel mai defavorabil caz, algoritmul poate necesita un numar excesiv de iteratii pana la terminare - fapt provocat nu de natura asincrona a algoritmului ci de alegerea arbitrara a conditiilor initiale; un caz in care apare un numar excesiv de iteratii chiar in varianta sincrona a algoritmului Bellman-Ford este ilustrat in urmatorul

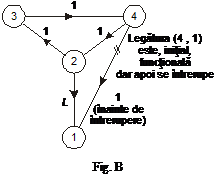
Exemplu Fie graful din fig. B, cu nodul 1 ca destinatie. Sa presupunem ca alegem drept conditii initiale cele mai scurte distante de la nodurile 2, 3 si 4 pana la nodul 1 inainte ca legatura (4 , 1) sa se defecteze, adica: D₂ = 3, D₃ = 2 si D₄

Dupa ce legatura (4 , 1) se defecteaza, sunt necesare aproape L iteratii pentru ca nodul 2 sa realizeze ca cea mai scurta cale de la el pana la nodul 1 este legatura directa . Acest exemplu ilustreaza asa-numitul "fenomen al stirilor proaste", conform caruia algoritmul raspunde lent la o crestere brusca a lungimii unei sau mai multor legaturi.

O metoda euristica permitand remedierea acestui neajuns este prezentata in [Bert ]. Alte posibilitati sunt prezentate in [Jaff ] si [Humb ].

In cel mai defavorabil caz, algoritmul necesita un numar excesiv de transmisii de mesaje. Un exemplu care ilustreaza faptul ca versiunea asincrona a algoritmului Bellman-Ford necesita mult mai multe transmisii de mesaje decat versiunea sincrona este prezentat in urmatorul

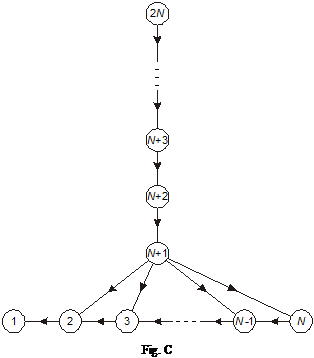
Exemplu Fie graful din fig. B, cu nodul 1 ca destinatie si cu toate legaturile de lungime 1.

Estimatele initiale ale celor mai scurte distante din toate nodurile sunt egale cu .

Sa consideram urmatoarea secventa de evenimente (pentru care toate mesajele sunt receptionate cu o intarziere nula

Nodul 2 isi actualizeaza cele mai scurte distante si comunica rezultatele nodului 3. La randul lui, nodul 3 isi actualizeaza cele mai scurte distante si comunica rezultatele nodului 4 si asa mai departe. Nodul N - 1 isi actualizeaza cele mai scurte distante si comunica rezultatele nodului N. In fine, nodul N isi actualizeaza cele mai scurte distante si comunica rezultatele nodului N + 1. In total se transmit N - 1 mesaje.

Nodul N + 1 isi actualizeaza cele mai scurte distante si comunica rezultatele nodului N + 2 si asa mai departe. Nodul 2N - 1 isi actualizeaza cele mai scurte distante si comunica rezultatele nodului 2N. Nodul N isi actualizeaza cele mai scurte distante. Exista N - 1 mesaje.

Pentru i = N - 1, N - 2, . , 2 (in aceasta ordine), nodul i isi comunica actualizarile nodului N + 1 si se repeta secventa 2. Sunt N  (N - 2) mesaje.

Numarul total de mesaje este N ² - 2. Daca algoritmul s-ar executa in mod sincron, cu trimiterea unui mesaj de la un nod catre vecinii sai doar atunci cand estimatele celor mai scurte distante se modifica, numarul necesar de mesaje ar fi 3 (N - 1) - 1. Dificultatea in versiunea asincrona consta in faptul ca o mare cantitate de informatie inutila soseste la nodul N + 1 prea devreme si declanseaza o multime de mesaje inutile de la nodul N + 1, care vor circula pana la nodul 2N.