Cautarea de siruri Knuth-Morris-Pratt

Cautarea de siruri Knuth-Morris-Pratt

In anul 1970 Knuth, Morris si Pratt au inventat un algoritm de cautare in siruri de caractere care necesita un numar de comparatii de ordinul n chiar in cel mai defavorabil caz.

Noul algoritm se bazeaza pe observatia ca avansul modelului in cadrul sirului cu o singura pozitie la intalnirea unei nepotriviri, asa cum se realizeaza in metoda anterioara, pe langa o eficienta scazuta, conduce la pierderea unor informatii utile.

Astfel dupa o potrivire partiala a inceputului modelului cu sirul,

Intrucat se cunoaste partial sirul (pana in punctul baleat),

Daca avem cunostinte apriorice asupra modelului obtinute prin precompilare,

Le putem folosi pentru a avansa mai rapid in sir.

Acest lucru este pus in evidenta de exemplul urmator in care:

Se cauta modelul MARGINE in textul sursa;

Caracterele care se compara sunt cele subliniate;

Dupa fiecare nepotrivire, modelul este deplasat de-a lungul intregului drum parcurs intrucat deplasari mai scurte nu ar putea conduce la o potrivire totala [4.3.3.a].

MAREA MARMARA SE MARGINESTE

MARGINE

MARGINE

MARGINE

MARGINE

MARGINE [4.3.3.a]

MARGINE

. . .

MARGINE

Utilizand predicatele P si Q, algoritmul KMP poate fi formulat astfel [4.3.2.b]:

i:= 0; j:= 0;

WHILE (j<m) AND (i<n) DO [4.3.3.b]

BEGIN

WHILE (j>=0) AND (s[i]<>p[j]) DO j:= d;

i:= i+1; j:= j+1

END;

Formularea algoritmului este aproape completa, cu exceptia factorului d care precizeaza valoarea deplasarii.

Se subliniaza faptul ca in continuare Q(i-j) si P(i-j,j) sunt invariatii globali la care se adauga relatiile 0<i<n si 0<j<m.

Este foarte important de subliniat faptul ca de aici inainte nu i va fi indicele care precizeaza pozitia primului caracter al modelului in sir ci valoarea i-j.

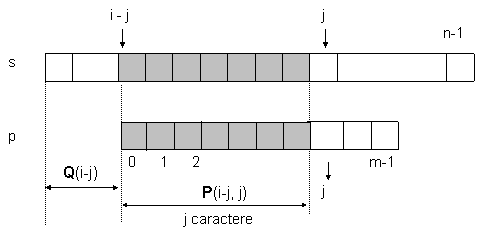
Indicele i precizeaza pozitia la care a ajuns procesul de cautare in sirul s (fig.4.3.3.a].

Fig. 4.3.3.a. Reprezentarea predicatelor P si Q in contextul cautarii KMP

Daca algoritmul se termina deoarece j = m, termenul P(i-j,j) al invariantului devine P(i-m,m), ceea ce conform relatiei care-l defineste pe P indica o potrivire incepand de la pozitia i-m .

Daca la terminare i = n si j < m, invariantul Q(i) implica absenta vreunei potriviri.

In vederea determinarii valorii lui d trebuie lamurit rolul atribuirii j:= d.

Considerand prin definitie ca d < j atunci atribuirea j:= d reprezinta o deplasare a modelului spre dreapta cu j - d pozitii.

Este evident ca este de dorit ca deplasarea sa fie cat mai lunga si in consecinta d cat mai mic posibil.

Pentru a determina valoarea lui d se prezinta doua exemple.

Exemplul 4.3.3.a. Se considera situatia din figura 4.3.3.b.

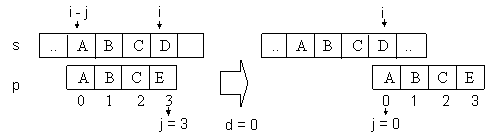
Fig. 4.3.3.b. Deplasarea modelului in cadrul sirului s. Cazul 1.

Se observa ca deplasarea se poate face peste 3 pozitii intrucat nu mai pot apare alte potriviri. In aceste conditii  d = 0 , iar atribuirea  j = d produce deplasarea cu  j-d = 3 pozitii.

X

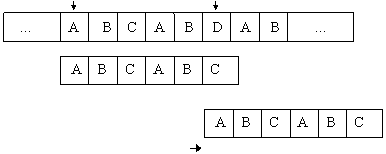
Exemplul 4.3.3.b. Se considera situatia din figura 4.3.3.c.

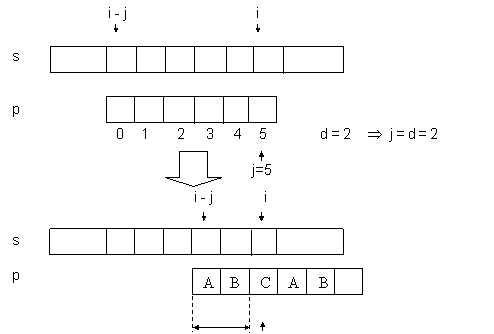
A B C A B C

A B C A B E

A B C A B C

0 1 2 3 4 5

d=2 j=2

Fig. 4.3.3.c. Deplasarea modelului in cadrul sirului s. Cazul 2.

In aceasta situatie deplasarea nu se poate face peste toata lungimea modelului intrucat mai exista o posibilitate de potrivire incepand de la i-2.

Acest lucru se intampla intrucat in cadrul modelului exista 2 subsecvente identice 'AB' de lungime 2.

Se noteaza cu d lungimea acestei subsecvente.

Dupa cum se observa din figura 4.3.3.c, deplasarea modelului la dreapta se poate face numai peste j-d (5 - 2 = 3) pozitii deoarece primele d pozitii ale modelului coincid cu cele d pozitii ale textului care preced indicele i (care indica neconcordanta).

In concluzie:

a) Initial exista o potrivire intre sirul s si modelul p incepand de la pozitia i-j pe lungime j adica este valabil invariantul P(i-j,j) & Q(i-j).

b) Dupa efectuarea deplasarii avem din nou o potrivire la i-d de lungime d adica este valabil invariantul P(i-d,d) & Q(i-d).

Aceasta situatie rezulta din observatia ca in model exista doua subsecvente identice de lungime d una la inceputul modelului alta de la pozitia j-d la j-1.

Formal acest lucru este precizat de relatia [4.3.3.c].

p₀ p_d-1 = p_j-d p_j [4.3.3.c]

Pentru ca lucrurile sa se desfasoare corect este necesar ca lungimea lui d sa fie maxima, adica sa avem cea mai lunga subsecventa care indeplineste conditiile precizate.

Rezultatul esential este acela ca valoarea lui d este determinata exclusiv din structura modelului si nu depinde de textul propriu-zis.

Din cele expuse rezulta ca pentru a-l determina pe d:

Pentru fiecare valoare a lui j

Se cauta in model cel mai mare d, adica cea mai lunga secventa de caractere a modelului care precede imediat pozitia j si care se potriveste ca un numar egal de caractere de la inceputul modelului.

Se noteaza valoarea d pentru un anumit j cu d_j.

Intrucat valorile d_j depind numai si numai de model, inaintea cautarii propriu-zise poate fi construit un tablou d cu aceste valori printr-un proces de precompilare a modelului.

Desigur acest efort merita sa fie depus daca  m << n. In continuare se prezinta trei situatii particulare de determinare a valorii deplasamentului d.

Exemplul 4.3.3.c. Se considera situatia din figura 4.3.3.d.

i - j i

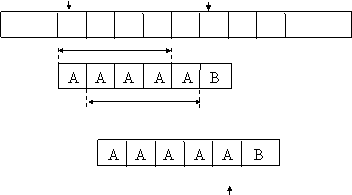
s A A A A A A A A

p

0 1 2 3 4 5 d₅ = 4 T j = d₅ = 4

p

j=4

0 1 2 3 4 5

j = 4

Fig. 4.3.3.d. Determinarea deplasamentului d . Cazul 1.

-----

Exemplul 4.3.3.d. Se considera situatia din figura 4.3.3.e.

i - j i

s

p

0 1 2 3 4 5 d₅ = 0 T j = d₅ = 0

p 

j = 0 0 1 2 3 4 5

Fig. 4.3.3.e. Determinarea deplasamentului d. Cazul 2.

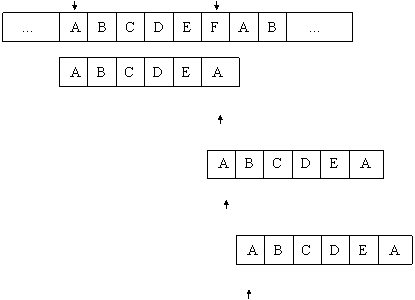
Exemplul 4.3.3.e. Se considera situatia din figura 4.3.3.f.

i - j i

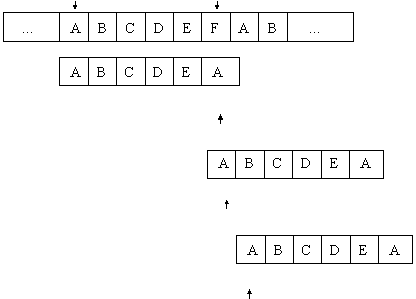
s 

p

0 1 2 3 4 5 d₅ = 0 T j = d₅ = 0

j = 5

p 

0 1 2 3 4 5

j = 0

p 

0 1 2 3 4 5

j = -1 d₅ = -1

Fig. 4.3.3.f. Determinarea deplasamentului d. Cazul 3.

Ultimul exemplu sugereaza ca se poate merge mai departe cu deplasarile si ca in loc sa se realizeze deplasarea peste 5 pozitii, in aceasta situatie se poate face peste intregul model deci  d₅ = -1  iar deplasarea se face peste 5 - (-1) = 6 pozitii.

Acest lucru este posibil deoarece primul caracter al modelului este identic cu ultimul sau caracter.

Intrucat s-a constatat necoincidenta pentru ultimul caracter al modelului, rezulta ca nu poate exista o coincidenta nici in cazul primului caracter al acestuia (identic cu ultimul), deci deplasarea se poate realiza peste el.

In aceste conditii, calculul lui d_j care presupune cautarea celor mai lungi secvente care se potrivesc in baza relatiei [4.3.3.c], poate fi completat dupa cum urmeaza.

Daca se constata ca  d_j = 0 si  p₀ = p_j , atunci se poate face d_j = -1 indicand deplasarea integrala a modelului fata de pozitia sa curenta in cadrul sirului s.

-----

In figura 4.3.3.g. apare un tablou demonstrativ in care pentru mai multe siruri model  p  se precizeaza structura tabloului d asociat adica valorile d_j corespunzatoare caracterelor modelului rezultate in urma precompilarii.

In stanga tabelului apare modelul p iar in dreapta tabelul d asociat.