Limbaje regulate

LIMBAJE REGULATE

1. Exemple practice de automate finite deterministe (AFD);
2. Definitia formala a unui AFD,

moduri de descriere;

limbaj recunoscut de un AFD

3. O metoda de definire a unui AFD care sa recunoasca un limbaj dat
4. Lema de pompare pentru limbaje regulate
5. Automate finite nedeterministe

definitie

echivalenta

6. Operatii de inchidere (regulate)
7. Expresii regulate

definitie

echivalenta

Diferentele dintre un AFD si un AFN sunt:

qIQ: pentru fiecare simbol aIS

in AFD pleaca o singura sageata,

0,

in AFN pleaca 1, sau

mai multe sageti;

Sagetile sunt etichetate:

in AFD: cu simboluri din S

cu simboluri din S

in AFN: cu simbolul vid, l

Modul de calcul

Definitie

AFN = (Q S d, q₀, F), unde:

Q = multime finita, nevida, ale carei elemente se numesc stari;

S = multime finita, nevida, numita alfabet de intrare, ale carei elemente se numesc simboluri;

d : Q x (S P(Q), numita functia de tranzitie;

q₀ IQ, numita starea initiala;

FÍQ numita multimea starilor finale.

Notatie

S_l S

Exemplu

AFN care recunoaste limbajul:

L₂=

Teorema

AFN AFD

Corolar

L S*, LIL₃: AFN care recunoaste L.

Definitie

Operatii de inchidere = operatii regulate =

• reuniunea,
• concatenarea,
• operatia star (*).

Teorema

L₃ este inchisa la reuniune, concatenare, operatia star.

Definitie

Expresie regulata =

o expresie R care satisface una dintre urmatoarele conditii:

1. aIS este o expresie regulata (reprezentand limbajul S
2. l este o expresie regulata (reprezentand limbajul S
3. este o expresie regulata (reprezentand limbajul vid);
4. daca R₁ si R₂ sunt expresii regulate T

(R₁ R₂) este o expresie regulata,

(R₁oR₂) este o expresie regulata,

(R₁*) este o expresie regulata.

Exemplu

Teorema

L S*, LIL₃: o expresie regulata R peste S care descrie L.

Definitie

AFNG = (Q, S d, q_start, q_accept), unde:

Q = multime finita, nevida, ale carei elemente se numesc stari;

S = multime finita, nevida, numita alfabet de intrare, ale carei elemente se numesc simboluri;

q_start IQ, numita starea initiala;

q_accept IQ, numita starea finala;

d : (Q ) x (Q ) R, numita functia de tranzitie.

CURS 2

LIMBAJE INDEPENDENTE DE CONTEXT (RECAPITULARE)

1. Definitii

gramatica

gramatica independenta de context

limbaj independent de context

2. Forme normale

definitie

exemple

aducerea la forma normala Chomsky

3. Lema de pompare

4. Operatii de inchidere

L₂ este inchisa la reuniune, concatenare, operatia *, omomorfism

L₂ nu este inchisa la intersectie si complementara

5. Automatul pushdown

• memoria finita a unui AFD nu poate memora numere n foarte mari.
• gramaticile independente de context (GIC)
• structura recursiva
• Domenii de utilizare a GIC:
• studiul limbilor naturale,
• Domenii de aplicabilitate
• specificarea si compilarea limbajelor de programare
• sintaxa unui limbaj de programare
• parsere

Nota:

Desi AFD si EXPR REG pot descrie un numar mare de limbaje, exista si limbaje - unele chiar destul de simple - pe care nu le pot descrie:

EX:

Motivul: memoria finita a unui AFD nu poate memora numere n foarte mari.

Un mecanism mai puternic este cel al GRAMATICILOR INDEPENDENTE DE CONTEXT (GIC)

Ele pot descrie unele aspecte care au o STRUCTURA RECURSIVA, fiind astfel utile intr-o varietate de domenii:

Un exemplu de UTILIZARE a GIC: STUDIUL LIMBILOR NATURALE.

Relatii dintre termeni precum: substantiv, verb, adjectiv, prepozitie, precum si dintre expersii substantivale, verbale etc. sunt - in mod natural - de tip recursiv:

O expresie verbala poate contine o expersie substantivala (de ex.) care, la randul ei, poate contine o expresie verbala sau adjectivala etc. Oei, o GIC poate modela in mod convenabil astfel de situatii

Un exemplu de APLICARE a GIC: SPECIFICAREA SI COMPILAREA LIMBAJELOR DE PROGRAMARE.

Sintaxa unui limbaj de programare poate fi invatata si pornind de la gramatica acestuia.

Proiectarea compilatoarelor si interpretoarelor de lb. de progr. Incepe deseori cu construirea unei GIC pt acel lb.

Cele mai multe compilatoare si interpretoare contin o componenta, numita PARSER, care extrage semnificatia unui program chiar inainte ca ca respectivul cod sa fie compilat sau ca instructiunea interpretata sa fie executata.

Acest proces de extragere a semnificatiei din codul programului se n. PARSING si permite "traducerea" codului scris intr-un lb. de progr. de nivel inalt intr-o forma mai adecvata executarii de catre calculator.

O posibila reprezentare a acestei semnificatii este arborele de derivare al codului (PARSING TREE) obtinut cu ajutorul GIC a lb. de progr. respectiv.

Exista numeroase metodologii care permit construirea - uneori automat - a unui parser direct din GIC a lb. de progr.

Reamintim ca:

1. Limbajele generate / descrise de G.I.C. se numesc L.I.C.;
2. Clasa L₂ L₃;
3. Un mecanism, care s-a dovedit a fi echivalent cu cel al G.I.C., este constituit de APD.

Definitia 1

Gramatica = (V,S P, S) unde:

V = multime finita, nevida, ale carei elemente se numesc variabile sau neterminale;

S = multime finita, nevida, numita alfabet de intrare, ale carei elemente se numesc terminale; V S

P = multime finita, nevida, ale carei elemente se numesc productii sau reguli de substitutie;

(ele descriu modul in care o variabila poate fi inlocuita cu o secventa de terminale si neterminale);

SIV se numeste variabila (simbolul) de start.

Exemplu

G₁=(, , , A)

Reprezentarea derivarilor:

• linear:

AT0A1T00A11T000A111T0³B1³T

• sintetic:

A _GT

• arbore de derivare:

Nota:

Exemplu

G₁=(, , , A)

O gramatica va calcula astfel:

P1) incepe cu productia / una dintre productiile in care in m.stg. apare smb. de start si inlocuieste smb. de start cu secventa din m. dr. ;

P2) alege o variabila din acest m.dr. si

o productie care contine acea variabila in m. sau stg.

si o inlocuieste cu m.dr. al acelei productii;

P3) se reia (Pasul 2) pana cand in m.dr. avem doar terminale.

Acest proces se numeste derivare si se poate reprezenta in mai multe moduri:

linear

AT0A1T00A11T000A111T0³B1³T

sintetic

A T

arbore de derivare

o derivare se incheie atunci cand frunzele arborelui de derivare sunt etichetate numai cu terminale.

Definitia 2

Gramatica independenta de context = (V,S P, S) a.i.

a b I P: |a|=1 si a I V.

Definitia 3

Limbaj independent de context = L.I.C. =

L(G)=

Exemplu

G₂=(, , , S) T

L₂

Nota:

Definitia 2

Gramatica independenta de context

o gramatica G=(V,S, P, S) in care fiecare productie are in m.stg. 1! singura variabila. ......

Definitia 3

Limbaj independent de context = L.I.C. =

limbajul descris de o G.I.C. .......

Exemplu

G₂=(, , , S) T

Limbajul parantezelor bine imbricate

Definitia 4

G I G.I.C. se afla in forma normala GREIBACH (FNG)

p I P, p : A aB, unde:

A I V,

a I S

B I (V S

Teorema 1

L=L(G) I L.I.C., l L: G' in FNG a.i. L=L(G').

Nota:

F.N. sunt standardizari ale GIC care faciliteaza anumite prelucrari, demonstratii, aplicari de algoritmi etc. Definitia 4

Definitia 4

G I G.I.C. se afla in forma normala GREIBACH (FNG)

orice productie din P este de forma A aB, unde: A I V,

a I S

B I (V S

Teorema 1

Orice LIC care nu contine cuvantul vid, poate fi generat de o GIC aflata in FNG.

Definitia 5

G I G.I.C. se afla in forma normala CHOMSKY (FNC)

p I P, p : A BC sau A a, unde:

A,B,C I V, B S C,

a I S

In plus, S l I P.

Lema 1 (demonstratia: EXERCITIU)

Fie G I G.I.C. aflata in FNC si L = L(G) T

wIL, |w|=n: |S _GT*w| = 2n-1, n I N.

Nota:

Definitia 5

G I G.I.C. se afla in forma normala CHOMSKY (FNC)

productie din P ested e forma A BC sau A a, unde:

A,B,C I V, B S C,

a I S

In plus, se admite productia S l

Lema 1

Fie L un LIC generat de o GIC aflata in FNC.

Atunci, lungimea oricarei derivari pentru un cuvant de lungime n este de 2n-1 ....

Teorema 2

L=L(G) I L.I.C.: G' in FNC a.i. L=L(G').

Demonstratie

Fie G = (V,S P, S), L = L(G); construim G'= (V₀,S , P₀, S₀), echivalenta, in FNC.

(P1) adaugam un nou simbol de start S₀ si

o noua productie: S₀ S

Nota:

Teorema 2

L=L(G) I L.I.C.: G' in FNC a.i. L=L(G').

Ideea demonstratiei:

Se aplica un fel de tranzitivitate a productiilor

Demonstratie

Fie G = (V,S P, S), L = L(G); construim G'= (V₀,S , P₀, S₀), echivalenta, in FNC.

Evident: S S dar V₀, P₀, S₀ se vor modifica astfel:

(P1) adaugam un nou simbol de start S₀ si

o noua productie: S₀ S

=> smb. de start al noii gramatici nu va aparea in m.dr. al nici unei productii,

adica se garanateaza conditia B S C.

(P2) eliminam productiile A l, A S;

apoi, pt fiecare aparitie a simbolul A in membrul drept al unei productii adaugam o productie similara in care simbolul A respectiv a disparut.

exemplul

Productia R uAvAw, u,v,w I (V S )*, este inlocuita cu:

R uvAw,

R uAvw,

R uvw,

exemplul

Productia R uAv, u,v I (V S )*, este inlocuita cu:

R uv

exemplul

Productia R A este inlocuita cu:

R à l (doar daca R l nu a fost deja eliminata).

(P3) inlocuim "perechile de productii unitare" de tipul:

A B,

B u, uI(V S

cu A u,

B u,

doar daca A u nu este o "regula unitara" care a fost deja eliminata.

(P4) pentru productiile "duble" de tipul:

A u₁u₂, unde u_i IV sau u_i I S, i=1,2

• se inlocuieste fiecare terminal u_i cu neterminalul U_i si
• se adauga o noua productie  U_i u_i, i=1,2

Nota:

(P3) inlocuim "perechile de productii unitare":

pt ca pe cele unitare singulare le-am tratat la pasul 2

Atentie: u este o secventa de terminale si neterminale, nu un singur simbol!!!!!

(P5) restul productiilor, adica cele de tipul:

A u₁u₂u₃.u_n, n ≥ 3 si i n: u_i IV sau u_i I S

se inlocuiesc, fiecare, cu setul de productii

A u₁A₁,

A₁ u₂A₂,

A₂ u₃A₃,

......

A_n-2 u_n-1u_n,

unde A₁, A₂, .,A_n-2 sunt noi variabile, adaugate lui V₀. q.e.d.

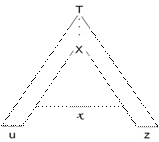
Lema de pompare pentru L.I.C.

Fie A S*, AIL.I.C. =>

pIN (constanta=lungimea de pompare) a.i.

sIA, |s| ≥ p u,v,x,y,zIS* cu proprietatile:

(i) s = uvxyz,

(ii) i ≥ o: uvⁱxyⁱz I A,

(iii) |vy| > 0,

(iv) |vxy| p.

Nota:

Ca si in cazul limbajelor regulate, lema de pompare pt LIC este utilizata pentru a demonstra ca un limbaj L nu este independent de context.

Lema de pompare pentru L.I.C.

Ideea demonstratiei:

Consideram arborele de derivare al unei secvente sIA f. lunga => arborele de derivare e f. adanc. =>

=> cel putin un terminal care apare in s si care eticheteaza o frunza din arborele de derivare al s si pentru care drumul care il leaga de radacina este f. lung. =>

=> pe acest drum cel putin un neterminal X care se repeta ca eticheta de nod =>

putem inlocui subarborele care are ca radacina a 2^a aparitie a lui X cu subarborele care are ca radacina prima aparitie a lui X (mai lung) si obtinem tot un arbore de derivare valid pentru G =>

=>obtinem tot o fraza din A

demonstratie

Constanta de pompare:

p = n^card(V)+2, unde n=|w|, A w I P.

Putem pp. ca n ≥ 2.

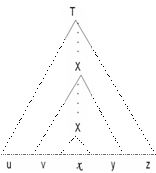
i=2  i=0

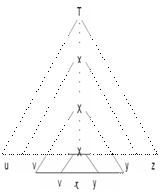
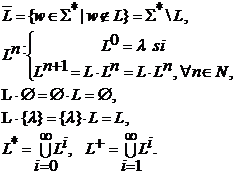Definitii 6 

L₁,L₂ S

L₁ L₂=,

L₁ L₂=,

L₁ L₂=,

L₁ ^o L₂=,

mi(L)=.

Lema 3

L.I.C. este inchisa la reuniune, concatenare si operatia *.

demonstratie

Fie L₁,L₂IL.I.C, L_i=L(G_i), unde G_i=(V_i,S_i,P_i,S_i), i=1,2:

L₁ L₂ este generat de G' V',S',P',S'), unde:

V'=V₁ V₂

S S S

S'=S₀,

P'=P₁ P₂

L₁ ^o L₂ este generat de G'=(V',S',P',S'), unde:

V'=V₁ V₂

S S S

S'=S₀,

P'=P₁ P₂

L* este generat de G'=(V',S',P',S'), unde:

V'=V

S S

S'=simbolul de start,

P'=P

Evident, toate cele 3 garamatici sunt independente de context.

Lema 4

L.I.C. este inchisa la operatia mirror si la omomorfism.

demonstratie

(i) Fie LIL.I.C, L=L(G), unde G=(V,S,P,S);  putem pp ca G este in FNC

=> construim G'=(V,S,P',S), unde

P'=

L(G')=mi(L), i.e. : S_G =>* w S _G'=>* mi(w), adica:

S=>x₁=>x₂=>.=>x_n este o derivare in G

S=>mi(x₁ >mi(x₂)=>.=>mi(x_n) este o derivare in G'.

n=1

=> x= l sau x I S => evident.

n≥1

Fie S_G =>* x, respectiv S _G'=>* mi(x) in n+1 pasi =>

1) Prima productie este S AB, respectiv S BA

2) yIS* a.i. x=yB => mi(x)=mi(yB)=Bmi(y)

=> lg derivarii lui y in G (mi(y) in G') este n

cf. ip.ind.

o derivare pt y in G iff o derivare pt mi(y) in G'.

compunere cu S AB (S BA)

S_G =>* x S _G'=>* mi(x).

(ii) Inchiderea la [substitutie] si omomorfism se dem. analog.

Lema 5

L.I.C. NU este inchisa la intersectie si complementara.

demonstratie

(i) Fie G₁=(,,,S},

G₂ ,,,S}.

=> L(G₁)= I L.I.C;

L(G₂)= I L.I.C.

Observam ca L(G₁) L(G₂)= L.I.C.

(ii) Ppa L.I.C. inchisa la complementara si fie LIL.I.C. >

Cum LIC - inchisa la reuniune si complementara(Lema3si pp noastra de mai sus)inseamna ca L₁ L₂ I LIC

=> L₁ L₂IL.I.C T L.I.C. inchisa la T contradictie cu (i).

APD reprezinta un nou model de calculabilitate

Stiva

AFN: 

APD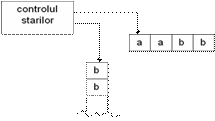

Nota:

APD reprezinta

un nou model de calculabilitate

puterea generativa similara G.I.C.

limbaje pt care caracterul de LIC poate fi mai usor demosntratat cu APD decat cu GIC.

Un APD seamana cu un AFN dar dispune de o componenta suplimentara: o STIVA.

Stiva ofera un spatiu de memorie suplimentar , potential nelimitat, pe langa cel finit al automatului: APD poate scrie (depune) smb. in stiva si le poate citi ulterior.

Obs. Accesul este insa secvential: APD poate citi doar smb. din varful stivei. Chiar si asa, el poate recunoaste limbaje nereg. precum :

citeste primul smb. de pe banda de intrare; pp. ca este 0;

APD depune acest smb. in stiva;

pp. ca si urmatoarele n smb. sunt 0 => APD le depune in stiva ca si pe primul;

pp. ca al n+2lea smb. citit este 1 => APD elimina un smb. 0 din stiva;

pp. ca si urmatoarele smb. citite de pe banda de intrare sunt 1 => APD elimina cate un smb. 0 din stiva pt fiecare smb. 1 citit;

daca la finalul citirii benzii de intrare stiva este vida inseamna ca nr total de smb 1 citite a fost egal cu nr total de smb o citite si depuse in stiva => secventa de intrare face parte din limbaj.

Observatii

AFD AFN

APDN ≥ APD

APDN, APD;

*}: APDN.

Nota:

Observatii

Din descrirea de mai sus se vede ca APD are intrinsec o natura nedeterminista.

APD poate fi det. sau nedet. Dar in timp ce AFN AFD, APDN au o putere generativa mai mare decat APD:

Exemplu: limbajul poate fi recunoscut si de un APDN si de un APD,

dar limbajul *} nu poate fi recunoscut decat de un APDN.

Deosebiri intre APD si AFD:

1) Doua alfabete, S si G

2) dom(d) = Q x (S ) x (G

3) codom(d) = P(Q x (G

Nota:

Deosebiri intre APD si AFD:

La APD trebuie sa luam in considerare nu numai banda de I si setul de stari ci si stiva;

simbolurile scrise in stiva pot fi preluate din acelasi alfabet / din alt alfabet decat cel al benzii de intrare => in definitia APD vom avea 2 alfabete: S si G

Urmatoarea actiune a APD este det. de:

starea crt. a APD,

simbolul citit de pe banda de intrare

simbolul aflat in varful stivei,

atentie: APD poate intalni si pe banda de intrare si in stiva smb. vid, l. =>..

Dom. de def. al functiei de trazitie d este Q x (S ) x (G

Urmatoarea actiune a APD poate consta in:

trecerea intr-o noua stare si EVENTUAL scrierea unui smb, in stiva.

In plus, modelul APD fiind intrinsec nedeterminist, APD poate trece in diferite stari=>codom(d)=P(Q x (G

Definitia 7

Automat pushdown=APD Q, S G d, q₀, F), unde:

Q = multime finita, nevida, ale carei elemente se numesc stari;

S = multime finita, nevida, numita alfabet de intrare, ale carei elemente se numesc simboluri, (S_l S

G= multime finita, nevida, numita alfabetul stivei, (G_l G

d : Q x S_l x G_l P(Q x G_l), numita functia de tranzitie;

q₀ IQ, numita starea initiala;

FÍQ numita multimea starilor finale.

Notatie

Observatie

• Metoda standard de testare a vidarii stivei: $ I G
• Metoda standard de testare a terminarii secventei de intrare: trecerea intr-o stare finala.

Teorema 3

Fie L S*. Atunci:

G I G.I.C.: L=L(G) A I APD: L=L(A).

Nota:

Notatie

APD, aflat in starea qi,

citeste smb. a de pe banda de intrare,

extrage smb. b din stiva,

depune smb. c in stiva.

Daca a = l T APD face tranzitia (chiar daca/si) fara sa citeasca nimic de pe banda de intrare;

Daca b = l T APD face tranzitia (chiar daca/si) fara sa extraga nimic din stiva;

Daca c = l T APD face tranzitia (chiar daca/si) fara sa depuna nimic din stiva.

Observatie

Definitia formala a APD NU contine nici un mecanism explicit de testare a vidarii stivei T

METODA STANDARD: se utilizeaza un smb. special din G, $, care este depus in stiva de la inceput;

cand acest smb. este intalnit (cand a ajuns in varful stivei) inseamna ca stiva s-a golit.

Analog, definitia formala a APD NU contine nici un mecanism explicit de testare a terminarii secventei de intrare T

METODA STANDARD: trecerea intr-o stare finala numai cand s-a incheiat citirea tuturor smb. de pe banda de intrare.

Teorema 3

Echivalenta dintre GIC si APD ca putere generativa

Fie L S*. Atunci:

G I G.I.C.: L=L(G) A I APD: L=L(A).

CURS 3

Masini Turing

1. Exemple

2. Definitia formala

3. Limbaje Turing-recunoscute si limbaje Turing-decidabile

Nota:

TM reprezinta un model de calcul mult mai puternic decat

AFD sau AFN (memorie finita) sau

APD (memorie infinita dar accesibila doar secvential).

Masina Turing (TM) a fost definita de matematicianul englez Alan TURING in 1936 ca un dispozitiv de calcul menit sa "calculeze orice functie intuitiv calculabila". In acest scop, A.Turing a inzestrat masina cu o memorie infinita si fara restrictii de acces si cu un dispozitiv de citire/scriere.

=> o MT poate face tot ce poate face un calculator real.

Totusi exista probleme pe care nicio MT (si nici un calculator real) nu le pot rezolva.

Aceste probleme transcend limitele teoretice ale calculabilitatii.

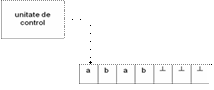
Nota:

1) Informal: O TM este un automat care dispune de:

O banda infinita, utilizata ca dispozitiv de memorare => o TM are memorie infinita;

Un cap de citire/scriere care se poate deplasa pe banda,

poate citi / scrie simboluri pe banda.

Initial, banda contine numai secventa de intrare si e vida in rest. Daca masina trebuie sa memoreze informatii, ea poate scrie aceste info. Pe banda. Si aceasta info. poate fi citita prin deplasarea capului de citire/scriere la stanga (inapoi) pe banda.

2) Masina calculeaza astfel:

Citeste un smb. de pe banda si se muta dintr-o stare in alta pana poate produce un rezultat. Aceasta revine la trecerea intr-o stare de acceptare sau de respingere, corespunzator acceptarii / respingerii secventei de intrare. Daca TM nu intra nici in starea de accepatre nici in starea de respingere, atunci, pe secventa respectiva de intrare, va cicla la infinit.

MT poate sa simuleze

• orice calculator real
• orice limbaj de programare.

Nota:

1) Care este deci relatia unei MT cu un calculator real?

Un calculator dispune de o memorie cu acces direct, in timp ce

memoria unei MT (banda ei de lucru) este scanata intotdeauna secvential (nu este permis nici un fel de salt). Prin scanari repetate si marcarea simbolurilor prelucrate, putem simula insa accesul direct la simbolurile de pe banda MT.

2) O MT poate fi privita si ca un limbaj de programare (foarte slab si primitiv dar capabil totusi sa programeze orice algoritm):

dispune de o structura de date (unica): stringul;

dispune de un set redus de instructiuni (de calcul si de test):

deplasarea cursorului la dreapta;

deplasarea cursorului la stanga;

citirea simbolului din celula curenta;

scrierea unui simbol peste simbolul din celula curenta;

alegerea uneia dintre operatiile de mai sus in functie de simbolul citit in celula curenta;

Exista variante de MT (numite enumeratoare) care, pe langa banda de intrare, dispun si de o "imprimanta" ca dispozitiv de iesire.

Exemplu

Fie L = *}. Construim o MT care sa testeze apartenenta unei secvente binare la L.

idee

avem voie sa ne deplasam la stanga si la dreapta in secventa de intrare si putem "marca" un simbol, odata ce l-am examinat.

Cursorul va scana in mod repetat secventa de intrare:

• la fiecare trecere va compara un simbol din stanga cu unul situat in dreapta lui # si, daca coincid, le inlocuieste cu x;
• daca toate simbolurile din secventa au fost inlocuite cu x, atunci MT trece in una dintre starile finale de acceptare; altfel trece in una dintre starile finale de respingere.

Nota:

Idee: ca la AFD, ne plasam in postura unei MT: citim o secv. kilometrica de smb si tb sa verificam daca ea consta din 2 subsecvente identice separate printr-un smb special.

Secventa e prea lunga pt a o putea "tine minte" intergal, dar avem voie sa ne deplasam la stg. si la dr. ei si, de asemenea, putem "marca" un smb odata ce l-am examinat.

=> algoritmul:

(P1) se scaneaza secventa de intrare wI* in cautarea simbolului special # ;

daca simbolul este gasit, atunci se trece la pasul 2; altfel, secventa este respinsa.

(P2) se scaneaza prima pereche de simboluri cele mai din stanga din cele 2 subsecvente;

daca coincid, atunci se inlocuiesc cu x si se trece la pasul 3; altfel, secventa este respinsa.

(P3) se scaneaza urmatoarea pereche de simboluri, pana se epuizeaza simbolurile din stanga lui #;

daca la dreapta lui # mai raman simboluri binare, atunci secventa de intrare w este respinsa; altfel, w este acceptata.

Definitia formala

Definitia 1

MT = un sistem (Q, S G d, q₀, q_a, q_r) unde:

Q = multime finita: multimea starilor;

S = multime finita: alfabetul de intrare; S Q=

G = multime finita: alfabetul benzii; S G VIG V S

d : Q x G Q x G x : functia de tranzitie;

q₀ I Q: starea initiala;

q_a I Q: starea finala de acceptare a secventei de intrare;

q_r I Q: starea finala de respingere a secventei de intrare.

Notatie

MT =

Observatie: Modul de calcul al MT:

1) Initial, MT se afla in starea q₀

si primeste pe banda, in primele n locatii din extr. stg., secventa de intrare w=w₁w₂.w_nIS

restul benzii este vida: locatiile sunt umplute cu simbolul blank ┴). Cum S nu contine smb. blank, primul blank ┴ care apare pe banda marcheaza sfarsitul secv. de intrare.

2) Cursorul se afla in extremitatea stanga a benzii (in prima locatie). Dupa lansarea MT in lucru, aceasta calculeaza cf. definitiei fctiei de tranzitie:

d(q,a)= (p,b,R)

MT, aflata in starea q, citeste pe banda de intrare simbolul a =>

• MT trece in starea p,
• inlocuieste simbolul a cu simbolul b in celula examinata si
• deplaseaza cursorul cu o celula la dreapta celulei examinate.

3) Daca MT incearca sa deplaseze cursorul dincolo de extremitatea stanga a benzii, acesta ramane in dreptul primei locatii din extremitatea stanga, chiar daca fctia de tranzitie indica - prin smb L - o deplasare la stg.

4) Calculul continua pana MT ajunge in q_a sau q_r si se opreste. Altfel, cicleaza nedefinit.

Definitia 2

Configuratie a unei MIMT = un triplet format din:

• starea curenta a M, q;
• continutul curent al benzii, v w;
• pozitia curenta a cursorului.

Notatie

vqw, v,wIG*, qIQ.

Exemplu

Configuratia 1011q₇01111 inseamna

Nota:

Am vazut ca, pe masura de MT calculeaza secv. de intrare, apar modificari ale:

starii crt. a MT,

continutului benzii,

pozitiei cursorului (indicata de primul simbol din w).

Un triplet de astfel de valori se n. configuratie a MT.

Definitia 3

Configuratia C₁ produce configuratia C₂

MT trece - corect - din C₁ in C₂ intr-un singur pas

Fie a,b,c I G

v,w I G

q_i, q_j I Q

Spunem ca o configuratie vaq_ibw produce configuratia vq_jacw daca d(q_i,b)=(q_j,c,L);

Analog: o configuratie vaq_ibw produce configuratia vacq_jw daca d(q_i,b)=(q_j,c,R).

Cazuri particulare de configuratii

1) Configuratia initiala: q₀w (MT este in starea initala si cursorul este in dreptul primului smb din secv. de intrare w);

2) Configuratii de oprire = nu produc o alta noua configuratie

• configuratia de acceptare : q=q_a, (= orice configuratie in care q=q_a;)
• configuratia de respingere : q=q_r; (= orice configuratie in care q=q_r;)

3) Cursorul este in extr. stanga a benzii => config. curenta q_ibw produce:

• q_jcw daca cursorul ramane pe loc, (evitam deplasarea lui dincole de extr. stg. a benzii);
• cq_jw daca cursorul se deplaseaza la dreapta;

4) Cursorul este in extr. dreapta a benzii =>

config. curenta vaq_i este echivalenta cu vaq_i┴ . => am redus acest caz part. la cazul general cu ┴ in loc de bw.

Limbaje Turing-recunoscute si limbaje Turing-decidabile

Definitia 4

MIMT M accepta secventa de intrare w IS

o secventa de configuratii C₁, C₂, ., C_s astfel incat:

C₁ este configuratia initiala a lui M pentru intrarea w,

i s-1: C_i C_i+1 ,

C_s este o configuratie de acceptare.

Definitia 5

Fie MIMT: L(M) = limbajul masinii Turing M = .

Nota:

L(M) = limbajul masinii Turing M = multimea frazelor peste S acceptate de M.

Definitia 6

Limbajul L S* se numeste Turing-recunoscut = recursiv enumerabil

MIMT: L=L(M).

Definitia 7

1) MIMT se numeste decidenta M se opreste indiferent ce secventa primeste la intrare.

2) Fie MIMT si L S*; Spunem ca M decide asupra limbajului L

(i) L=L(M),

(ii) M este decidenta.

Nota:

O MT poate esua asupra unei secv. de intrare daca:

Intra in starea q_r si deci respinge secventa;

2) Intra intr-o ciclare infinita (ceea ce nu inseamna neaparat repetarea aceleasi secv. de pasi ci o comportare mai mult sau mai putin complexa care insa nu duce niciodata in una dintre starile finale q_a sau q_r.

=> Pot aparea situatii in care MT calculeaza un timp indelungat fara a produce niciun rezultat si totusi NU SE POATE DECIDE daca acest fapt se indica

T    intrarea in ciclare sau pur si simplu

T    un calcul f. complicat care cere f. mult timp.

=> E preferabil sa lucram cu MT care, pt. secv. de intrare, se opresc (nu cicleaza niciodata). Astfel de MT se n. decidente.

Definitia 8

Limbajul L S* se numeste [Turing-]decidabil = recursiv

MIMT decidenta: L=L(M).

Nota:

Adica: L este recunoscut de o MT care se opreste indiferent de secventa primita la intrare.

Observatie

L Turing-decidabil => L este Turing-recunoscut dar

(rec.) (r.e.)

<

Nota:

L Turing-recunoscute care nu sunt Turing-decidabile

Exemplul 1

L₁ = {wI nIN: |w|=2n+1} este Turing-decidabil =>

M₁="Fie secventa de intrare wI

1. Daca pe banda de intrare ! simbol, atunci M₁ accepta; altfel, se aduce cursorul in extremitatea stanga a benzii.
2. Se scaneaza banda si se bareaza primul simbol intalnit (nemarcat).

Daca nu exista, atunci M₁ respinge.

3. Se scaneaza banda si se bareaza primul simbol intalnit (nemarcat).

Daca nu exista, atunci M₁ accepta; altfel, se aduce cursorul in extremitatea stanga si se reia de la Pasul 2."

Definim formal M₁=(, S G d, q₀, q_a, q_r)

unde d

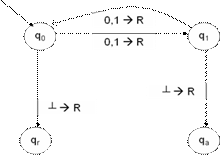
Exemplu de secventa acceptata de M₁: 

q₀101 = q₀101┴ 1q₁01┴ 10q₀1┴ 101q₁┴ 101q_a

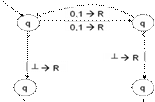
Exemplu de secventa respinsa de M₁:

q₀1011 = q₀1011┴ 1q₁011┴ 10q₀11┴ 101q₁1┴ 1011q₀ ┴ 1011q_r.

Exemplul 2

L₂ = este Turing-decidabil =>

M₂="Fie secventa de intrare wI

1. Se scaneaza banda de la stanga la dreapta;

daca se intalneste un simbol diferit de 0, atunci M₂ respinge.

2. Se aduce cursorul in extremitatea stanga si se scaneaza banda, barandu-se simbolurile 0 din 2 in 2, incepand cu primul 0 nebarat intalnit.

3. Daca la Pasul 2 banda continea un singur simbol 0, atunci M₂ accepta.

4. Daca la Pasul 2 banda continea mai mult de un simbol 0 si numarul de simboluri 0 era impar, atunci M₂ respinge.

5. Se readuce cursorul in extremitatea stanga a benzii.

6. Se reia Pasul 2."

Definim formal

M₂ ,

S G d, q₁, q_a, q_r),

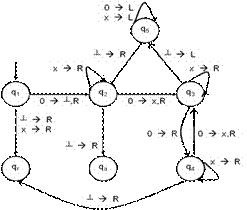
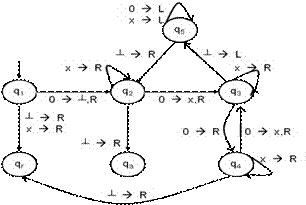
Nota:

Explicam codificarea folosita:

Eticheta 0 ┴,R de pe tranzitia de la q₁ la q₂ inseamna ca MT aflata in starea q₁ citeste de pe banda smb. 0;

ca urmare, MT trece in starea q₂, depune smb blank in celula citita si deplaseaza cursorul catre dreapta,

adica: sageata, cele 2 stari pe care aceasta le leaga si eticheta sagetii corespund tranzitiei: d(q₁,0)= (q₂,┴,R).

Eticheta 0 R de pe tranzitia de la q₃ la q₄ inseamna ca MT aflata in starea q₃ citeste de pe banda smb. 0;

ca urmare, MT trece in starea q₄, nu modifica insa continutul celulei (benzii) si deplaseaza cursorul catre dreapta,

adica: sageata, cele 2 stari pe care aceasta le leaga si eticheta sagetii corespund tranzitiei: d(q₃,0)= (q₄,0,R).

Modul de lucru al M₂:

Ea incepe prin a depune un blank peste cel mai din stanga 0 de pe banda => Mt va putea determina, la Pasul 5, extr. stg. a benzii (puteam folosi ca delimitator stanga un smb special, ca de ex. #, dar am fi marit alfabetul G si am fi complicat diagrama.

Exemplu de secventa acceptata de M₂:

q₁0000 ┴q₂000 ┴xq₃00 ┴x0q₄0 ┴x0xq₃┴ ┴x0q₅x┴ ┴xq₅0x┴ ┴q₅x0x┴ q₅┴x0x┴ ┴q₂x0x ┴ ┴xq₂0x ┴

┴xxq₃x┴ ┴xxxq₃┴ ┴xxq₅x┴ ┴xq₅xx┴ ┴q₅xxx┴ q₅┴ xxx┴ ┴q₂xxx┴ ┴xq₂xx┴

┴xxq₂x┴ ┴xxxq₂┴ ┴xxx┴q_a

Observatie

Testul din Pasul 4 al MT M₂ se poate efectua si prin apelarea MT M₁.

Nota:

=> diagrama de stare trebuie modificata corespunzator.

Observam ca MT pot modela si capacitatea calculatoarelor reale de a rula programe care apeleaza alte programe.

Exercitii

MT pentru limbajele:

L₃ = { w#w | w I

L₄ = ;

L₅ = { #x₁#x₂##x_n| x_iI* si x_i x_j, i j n, nIN }.

CURS 4

Variante de masini Turing

1. Terminologia de descriere a MT
2. MT cu 3 "deplasari"
3. MT cu mai multe benzi
4. MT nedeterministe
5. Enumeratoare
6. Echivalenta modelelor de calculabilitate
7. Problema a 10-a a lui Hilbert

Terminologia de descriere a MT

O MT poate fi descrisa in 3 moduri:

• formal:

sunt date complet Q, S G d

• la nivelul implementarii MT:

se utilizeaza limba naturala pt a defini:

modul in care se deplaseaza cursorul,

modul de memorare a informatiei de pe banda de lucru;

• la nivelul cel mai inalt:

se utilizeaza limba naturala pt a descrie un algoritm, ignorand complet modul de implementare a acestuia.

Definim formatul si notatia utilizate pt a descrie o MT:

datele de intrare constau intotdeauna dintr-o secventa de simboluri;

daca intrarea trebuie sa fie un obiect (un graf, un polinom, un automat etc. sau o combinatie a acestora), atunci va trebui mai intai sa-l reprezentam printr-o secventa.

Intrucat codificarile alternative pot fi decodifcate unele in altele de catre MT (eficient) => putem alege orice codificare pt obiectul de intrare.

Vom nota

• 1! obiect O, codificat printr-o secventa, prin <O>;
• mai multe obiecte O₁,O₂,..,O_n, codificate printr-o unica secventa, prin < O₁,O₂,..,O_n >.
• prima linie a textului va descrie datele de intrare ale MT;
• daca intrarea este:
• chiar o secventa de simboluri w => ea este interpretata ca un cuvant peste un alfabet si notata w;
• codificarea unui obiect <A> => MT incepe automat cu VERIFICAREA CORECTITUDINII CODIFICARII.
• algoritmul este impartit in etape pasi de calcul numerotati;
• bloc indentare.

Problema

Sa se gaseasca un algoritm care sa verifice daca un graf neorientat oarecare este conex sau nu.

Formalizare

Fie A = un limbaj care consta din toate secventele care reprezinta grafuri neorientate conexe =>

A = ;

trebuie sa gasim o MT decidenta care sa decida asupra limbajului A.

M = "Fie intrarea <G> (adica: o codificare a grafului G):

1. Se selecteaza "primul" nod din G si se marcheaza.

2. Se reia pasul urmator pana cand nu se mai pot marca noi noduri:

3. Fie un nod oarecare v din G; daca el este legat printr-o muchie de un nod deja marcat, atunci nodul v trebuie marcat si el.

4. Se scaneaza toate nodurile din G pt a verifica daca sunt toate marcate sau nu. Daca sunt marcate toate nodurile, atunci M accepta; altfel, M respinge."

Exemplu

<G>=((1,2,3,4);(1,2),(1,3),(1,4),(2,3)).

Explicam modul de codificare a lui G:

MT incepe prin a verifica corectitudinea codificarii <G>.

Daca testul se incheie cu succes (codificarea e corecta), atunci MT trece la prima etapa a algoritmului.

MT cu 3 "deplasari"

Exemplu

Fie MT = (Q, S G d, q₀, q_a, q_r) unde:

d : Q x G Q x G x ;

Fie MT' = (Q', S G d', q'₀, q'_a, q'_r) unde:

d Q' x G Q' x G x ;

d q_i, a) = (q_j,b,S)

d (q_i, a) = (q_k,b,R), d (q_k, b) = (q_j,b,L).

=> Cele 2 modele sunt computational echivalente dar:

• e nevoie de cate o o stare auxiliara suplimentara;
• sunt necesare 2 tranzitii in loc de una.

Nota:

Vom arata ca MT este un model de calculabilitate ROBUST,

i.e.: MT standard, cu n benzi, nedet, recunosc aceeasi clasa de limbaje.

(si AFD si APD sunt destul de robuste dar nu la fel de robuste ca MT!!!)

Exemplu

Fie MT = (Q, S G d, q₀, q_a, q_r) unde:

d : Q x G Q x G x ;

Fie MT' = (Q', S G d', q'₀, q'_a, q'_r) unde:

d Q' x G Q' x G x ;

Adica: cursorul se poate deplasa la stg/dr. sau poate ramane pe loc.

MT si MT' recunosc aceeasi clasa de limbaje pt ca fiecare tranzitie a MT' de forma

d q_i, a) = (q_j,b,S)

poate fi simulata prin 2 tranzitii de forma:

d (q_i, a) = (q_k,b,R), d (q_k, b) = (q_j,b,L)

=> Cele 2 modele sunt computational echivalente dar "pretul" simularii MT cu 3 "deplasari" de catre o MT cu 2 "deplasari" este:

spatiu de memorie mai mare (e nevoie de cate o stare auxiliara suplimentara);

timp de executie mai lung (e nevoie de 2 tranzitii in loc de una).

In continuare, vom da pentru MT doar descrierea la nivelul cel mai inalt; din ea se poate deriva relativ usor functia de tranzitie.

MT cu mai multe benzi

Definitia 1

O MT cu mai multe benzi este o MT standard

M = (Q S G d, q₀, q_a, q_r) care:

(i) are n 1 benzi de lucru si n 1 cursoare corespunzatoare;

(ii) initial prima banda contine secventa de intrare iar celelalte n-1 benzi sunt vide;

(iii) d : Q x Gⁿ Q x Gⁿ x ⁿ,

d(q_i,a₁,a₂,.,a_n) = (q_j,b₁,b₂,.,b_n,L,R,S,L,.,S).

Nota:

Definitie

O MT cu mai multe benzi este o MT standard

M = (Q S G d, q₀, q_a, q_r) care:

(i) are n 1 benzi de lucru si n 1 cursoare corespunzatoare;

(ii) initial prima banda contine secventa de intrare iar celelalte n-1 benzi sunt vide;

(iii) Functia de tranzitie este modificata pt a permite cursoarelor sa citeasca, sa scrie si sa se deplaseze pe unele sau pe toate benzile simultan:

d : Q x Gⁿ Q x Gⁿ x ⁿ,

d(q_i,a₁,a₂,.,a_n) = (q_j,b₁,b₂,.,b_n,L,R,S,L,.,S);

Adica: MT se afla in starea q_i si cursorul k citeste simbolul a_k de pe banda k, 1 k n. Ca urmare, MT trece in starea q_j iar cursorul k scrie pe banda k simbolul b_k, 1 k n, dupa care se deplaseaza la dr/stg sau ramane pe loc.

Aparent mai puternice, si MT cu mai multe benzi sunt computational echivalente cu MT standard pt ca MT cu mai multe benzi poate fi simulata cu o MT standard.

Teorema 1

M = MT cu mai multe benzi =>

S = MT standard a.i. L(S) = L(M).

ideea demonstratiei

Fie M = (Q, S G d, q₀, q_a, q_r) o MT cu n 2 benzi si

S = (Q', S G d', q'₀, q'_a, q'_r) o MT standard.

Nota:

Teorema 1

Pentru orice MT cu mai multe benzi se poate construi o MT standard, echivalenta.

ideea demonstratiei

Fie M = (Q, S G d, q₀, q_a, q_r) o MT cu n 2 benzi si

S = (Q', S G d', q'₀, q'_a, q'_r) o MT cu 1! banda.

Vom simula MT M cu ajutorul MT S memorand info. de pe cele n 2 benzi ale M pe banda (unica) a lui S.

Exemplu:

=>

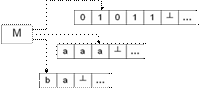=> (i) un simbol aditional #, pt delimitator;

(ii) aIS a IG

=> S devine o MT cu mai multe benzi si cursoare virtuale.

Nota:

Exemplu

=> In acest scop am folosit:

(i) un simbol aditional, #, ca delimitator, pentru a separa pe unica banda a lui S, cele n secvente de pe cele n benzi ale M;

(ii) cate un nou simbol pt fiecare simbol din S, pt a simula pozitia cursorului corespunzator (adica: pt fiecare simbol aI G adaugam in G' simbolul a

=> S devine o MT cu mai multe benzi si cursoare virtuale.

demonstratie

S = "Fie secventa de intrare w=w₁w₂.w_kIS

1. S isi formateaza banda de intrare pt a reprezenta cele n benzi ale M, la momentul initial:

#w₁'w₂w₃.w_k#

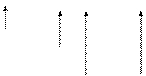
banda 1

banda 2

banda 3..banda n

2. S scaneaza unica sa banda de la primul delimitator # pana la cel de-al (n+1)lea delimitator # in scopul de a determina simbolurile aflate in dreptul cursoarelor virtuale.

Apoi, S mai face o parcurgere pentru a actualiza benzile virtuale conform definitiei functiei de tranzitie a lui M;

3. Daca S deplaseaza unul dintre cursoarele virtuale la dreapta unui delimitator #, aceasta inseamna ca M a mutat cursorul corespunzator peste portiunea vida a benzii respective. => S:

• depune simbolul special in celula respectiva de pe unica sa banda,
• deplaseaza continutul benzii sale, de la acea celula pana la cel mai din dreapta delimitator #, cu o celula la dreapta.

Apoi, continua simularea ca mai sus."

Corolar 1

L S* este Turing-recunoscut

o MT cu mai multe benzi, M, a.i. L=L(M).

demonstratie

"T

MT standard este o MT cu mai multe benzi triviala (n = 1).

"

Fie MIMT, M are mai multe benzi: L=L(M);

Cf. Teoremei 1, SIMT standard, echivalenta cu M;

T L = L(S).

MT nedeterminsite

• MTN ≈ AFN, APDN;
• Modelul de calcul: arbore;
• MTN accepta secventa de intrare

cel putin una dintre ramurile arborelui are ca eticheta a frunzei o configuratie de acceptare.

Definitia 2

O MT nedeterminista este o MT standard

M = (Q S G d, q₀, q_a, q_r) unde:

d : Q x G P(Q x G x ).

Teorema 2

N = MT nedeterminista =>

S = MT standard a.i. L(S) = L(N).

ideea demonstratiei

Fie N o MT nedeterminsita;

este suficient sa construim o MT, M, cu trei benzi care sa simuleze N deoarece,

conform Teoremei 1, vom putea apoi sa construim o MT standard, S, care sa o simuleze pe M.

• M va incerca toate ramurile de calcul posibile ale N;
• daca va ajunge vreodata in starea q_a atunci M recunoaste secventa de intrare, altfel simularea nu se va termina.
• Cautarea unei configuratii de acceptare efectuata de M in arborele lui N:

1. DEPTH FIRST;
2. BREADTH FIRST.

cazul (1): exploram in adancime o ramura infinita si ignoram una valida..

cazul (2): sigur vom examina toate nodurile arborelui pana gasim configuratia de acceptare

Nota:

Vom simula MT nedeterminsita N cu o MT determinista cu mai multe benzi M astfel:

pentru fiecare secventa de intrare primita, M va incerca toate ramurile de calcul posibile ale N;

daca va ajunge vreodata in starea q_a atunci M va recunoaste secventa de intare respectiva, altfel, simularea nu se va termina;

cautarea efectuata de M in arbore pt a gasi o configuratie de acceptare se poate face DEPTH FIRST sau BREADTH FIRST.

Prima strategie pare mai indicata dar nu este!!!!: putem explora in adancime o ramura de calcul infinita si sa ignoram astfel o ramura valida!!!

=> utilizam metoda BREADTH FIRST: vom vizita toate nodurile de pe nivelul n inainte de a trece la nodurile de pe nivelul n+1;

=> astfel suntem siguri ca vom examina toate nodurile arborelui pana gasim configuratia de acceptare.

demonstratie

Fie d : Q x G P(Q x G x ) functia de tranzitie a lui N.

Notam b=max)=codom(d

=> b=nr max de cop i pe care ii poate avea un nod din arborele de derivare al lui N

Notam cu S_b

Construim o MT determinista M cu 3 benzi astfel:

• banda 1: contine permanent cuvantul de intrare;
• banda 2: contine si actualizeaza permanent un duplicat al continutului benzii de lucru a lui N, reprezentand una dintre ramurile de calcul nedeterminist efectuat de N;
• banda 3: tine evidenta pozitiei din arbore in care se afla S .

banda de intrare

banda de simulare

banda de adresa

Banda 3 contine in orice moment un cuvant aIS_b

acest cuvant reprezinta:

• fie una dintre ramurile de calcul nedeterminist efectuat de N, de la radacina pana la nodul a carui adresa este exact a
• fie o adresa nevalida

Nota:

Explicitam modul in care este reprezentata informatia pe banda 3:

intrucat fiecare nod din arborele de calcul (derivare) al N poate avea maximum b copíi (cf. obs. de mai sus),

vom asocia fiecarui nod din arbore inca o adresa (eticheta), sub forma unui cuvant peste alfabetul S_b

Astfel,

adresa nodului-radacina este cuvantul vid, lI S_b

daca un nod are adresa 231 inseamna ca ajungem la nodul respectiv plecand din radacina catre al doilea ei fiu, apoi la al treilea fiu al fiului radacinii (nepot!) si, in fine, la primul fiu al acestuia (stranepot!))

ATENTIE! nu toate cuvinetele peste S_b pot fi adrese valide de-a lungul unei ramuri de calcul: de ex. simbolul urmator din secventa este un simbol aIS_b dar nodul-tata are mai putin de a copii.

Pe de alta parte, fiecare simbol dintr-o secventa valida din S_b va indica urmatoarea alegere care trebuie facuta atunci cand trebuie simulat un pas pe una dintre ramurile calculului nedeterminist efectuat de N.

Prin urmare, banda 3 contine in orice moment un cuvant aIS_b

acest cuvant reprezinta:

T    fie una dintre ramurile de calcul nedet. efectuat de N, de la radacina pana la nodul a carui adresa este exact a

T    fie o adresa nevalida (vezi mai sus).

M="Fie secventa de intrare w:

1. Initial, banda 1 contine cuvantul de intrare w , banda 2 este vida iar pe banda 3 se genereaza primul cuvant aIS_b

2. Se copiaza continutul benzii 1 pe banda 2.

3. Se utilizeaza banda 2 pentru a simula una dintre ramurile calcului nedeterminist efectuat de N pe intrarea w.

Inainte de a simula un pas de calcul efectuat de N, M examineaza simbolul urmator de pe banda 3 pt a determina care dintre posibilitatile de continuare oferite de d_N trebuie aleasa.

Daca nu mai sunt simboluri pe banda 3, atunci se trece la Pasul 4.

Daca alegerea facuta este nevalida, atunci se trece tot la Pasul 4.

Daca s-a intrat intr-o configuratie de respingere, se merge tot la Pasul 4.

Daca s-a intrat intr-o configuratie de acceptare, M recunoaste intrarea w si se opreste.

4. Se inlocuieste secventa de pe banda 3 cu urmatorul cuvant peste S_b, in ordine lexicografica. Se simuleaza urmatoarea ramura de calcul al N reluand de la Pasul 2."

Corolar 2

L S* este Turing-recunoscut

o MT nedeterminista, N, a.i. L=L(N).

demonstratie

T

MT standard este o MT nedeterminista triviala.

Fie NIMT, N este nedeterminista: L=L(N);

Cf. Teoremei 2, SIMT standard, echivalenta cu N;

T L = L(S).

Definitie 3

O MT nedeterminista se numeste decidenta

wIS*, toate ramurile ei de calcul se opresc.

Corolar 3

L S* este decidabil

o MT nedeterminista decidenta, N, a.i. L=L(N).

Enumeratoare

Limbajele Turing recunoscute = limbaje recursiv enumerabile

Enumerator

Imprimanta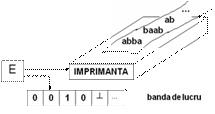  

Modul de lucru:

• initial: banda de intrare este vida;
• limbajul enumerat de E: multimea tuturor secventelor de simboluri printate de imprimanta;
• situatia de ciclare: tiparirea unei liste infinite de cuvinte.

Teorema 3

Fie L S*; L este Turing-recunoscut

EIMT a.i. L=L(E).

demonstratie

Fie EIMT a.i. L=L(E).

M=" Fie secventa de intrare w:

1. Se ruleaza enumeratorul E pe intrarea w.

De fiecare data cand E printeaza un cuvant, se compara acest cuvant cu secventa w.

2. Daca apare o coincidenta, atunci M accepta."

Evident, M accepta secventele din lista tiparita de E.

T

Fie MIMT a.i. L=L(M).

E=" Indiferent care este cuvantul de pe banda de intrare a lui E, acesta este ignorat:

1. Pentru fiecare i=1 ,. se repeta urmatorii pasi:

2. M executa i pasi de calcul pentru fiecare cuvant de intrare s₁,s₂,.,s_iIS

3. Daca vreunul dintre cei i pasi de calcul aduce M intr-o configuratie de acceptare, atunci cuvintele corespunzatoare din sirul s₁,s₂,.,s_i sunt tiparite de imprimanta lui E."

Observatii

1. Pentru a construi E a fost nevoie se o listare a cuvintelor din S: orice listare (fara repetitii) este acceptabila.
2. Evident, daca M accepta un cuvant oarecare sIS*, acesta apare la un moment dat in lista tiparita de E. De fapt, el va fi tiparit de o infinitate de ori deoarece M reia calculul de la pasul 1 pt fiecare i, oridecateori lista s₁,s₂,.,s_i se lungeste cu inca un cuvant.
3. Procedura de mai sus simuleaza rularea lui M in paralel pe toate cuvintele de intrare posibile:
4. i=1 s₁ 1 pas de calcul
5. i=2 s₁ 2 pasi de calcul
6. s₂ 2 pasi de calcul
7. i=3 s₁ 3 pasi de calcul
8. s₂ 3 pasi de calcul acceptat
9. s₃ 3 pasi de calcul
10. i=4 s₁ 4 pasi de calcul acceptat
11. s₂ 4 pasi de calcul acceptat
12. s₃ 4pasi de calcul
13. s₄ 4 pasi de calcul acceptat
14. .........................

Echivalenta modelelor de calculabilitate

Am definit mai multe variante de MT si am demonstrat echivalenta lor .

Exista si alte modele de calculabilitate:

• functiile l-calculabile: Alonzo CHURCH, Stephen Cole KLEENE,1934
• functiile general recursive: Kurt Godel, 1935
• sistemele (masinile) Post: Emil POST, 1936
• algoritmii normali Markov: A.A.MARKOV, 1954.

Toate au aceeasi caracteristica: acces nerestrictionat la o memorie nelimitata.

In plus, toate sunt echivalente cu MT (si deci unele cu altele

=> clasa algoritmilor pe care o descriu este unica si naturala.

vezi si clasa limbajelor de programare.

Problema a 10-a a lui Hilbert

Algoritm: o notiune primara

Problema a 10-a a lui Hilbert

Nota:

Algoritmii au o istorie lunga in matematica (gasirea numerelor prime, a cmmdc etc.) dar notiunea insasi nu a capatat (inca) o definitie matematica precisa, lucru esential pentru rezolvarea unor probleme importante, care au - de cele mai multe ori - conotatii filosofice.

Se opereaza insa cu notiunea intuitiva de algoritm, se folosesc descrieri, proprietati etc.

Lipsa unei definitii riguroase a avut nu numai urmari "dramatice" pt posibilitatea de a rezolva o serie de probleme importante dar a avut si conotatii filosofice dintre cele mai semnificative.

Vom ilustra acest fapt prin intermediul unei probleme celebre, problema a 10-a a lui Hilbert.

Congresul International al matematicienilor, 1900, Paris;

Conferinta lui David HILBERT: lista celor 23 probleme

Observatii

• ". un proces cu ajutorul caruia, dupa un numar finit de operatii, sa se determine .."
• Hilbert presupunea ca algoritmul exista si trebuie doar descoperit.
• Lipsa unei definitii formale pentru notiunea de algoritm solutii pentru cazuri particulare ale problemelor dar nu pentru o clasa intreaga.

Nota:

La Congresul International al matematicienilor care a avut loc in anul 1900 la Paris, matematicianul german David HILBERT a tinut o conferinta devenita celebra. In aceasta conferinta, Hilbert a identificat 23 de probleme pe care le-a considerat a fi o provocare adresata matematicienilor secolului XX. Cea de-a 10a problema din lista implica notiunea - neformalizata - de algoritm:

sa se gaseasca un algoritm care sa verifice daca un polinom in oricate variabile admite o radacina in Z.

Observatii.

David Hilbert nu a folosit termenul de algoritm ci formularea: ". un proces cu ajutorul caruia, dupa un numar finit de operatii, sa se determine .."

Enuntul problemei indica faptul ca Hilbert nu se indoia de existenta unui astfel de algoritm; el considera dificila doar gasirea lui.

Notiunea intuitiva, neformalizata, de algoritm cu care operau matematicienii la inceputul secolului XX le permitea sa gaseasca algoritmi pentru anumite cazuri particulare ale unor probleme dar in niciun caz nu le putea permite sa DEMONSTREZE inexistenta unui algoritm pt rezolvarea unei CLASE de probleme. Pt acest lucru era nevoie de de definitia riguroasa a notiunii de algoritm.

Teza Church-Turing

Problema a 10a a lui Hilbert.

1970, Yuri MATIJASEVIČ, (Martin DAVIS, Hilary PUTNAM, Julia ROBINSON):

nu exista nici un algoritm care sa verifice daca un polinom oarecare are radacini intregi

Problema a 10a a lui Hilbert este nerezolvabila algoritmic.

Nota:

Aceasta definitie a aparut in anul 1936 in lucrarile lui A. Church si A. Turing.

Asa cum am aratat, primul este autorul formalismului notational denumit l-calcul; al doilea al masinilor omonime.

Imediat s-a demonstrat echivalenta celor 2 definitii matematice.

Relatia dintre aceste definitii matematice riguroase si notiunea informala de algoritm este cunoscuta sub numele de teza Church-Turing:

Clasa alg. (fctiilor intuitiv calculabile) coincide cu clasa fctiilor l-calculabile (fctiilor calculabile cu MT).

Aceasta teza a furnizat o definitie pentru notiunea de algoritm suficienta (si necesara) pentru a rezolva Problema a 10a a lui Hilbert. In 1970, Yuri MATIJASEVIČ, bazandu-se pe rezultate anterioare datorate lui Martin DAVIS, Hilary PUTNAM, Julia ROBINSON, arata ca nu exista nici un algoritm care sa verifice daca un polinom oarecare are radacini intregi ( .Problema a 10a alui Hilbert este nerezolvabila algoritmic.)

Fie D =

D este decidabila ?

D este Turing-recunoscuta dar nu este decidabila.

Cazul unar:

Fie D₁=.

Construim o MT, M₁, care recunoaste D₁:

M₁ = "Fie p₁ un polinom oarecare in variabila x:

1. Se evalueaza p₁ succesiv pentru x=0, x=1, x=-1, x=2, x=-2, x=3

2. Daca la un moment oarecare se obtine 0, atunci M₁ accepta p₁."

Cazul general:

putem construi o MT, M, similara care va testa fiecare polinom de intrare p pentru diferite combinatii de valori, in functie de numarul de variabile.

n=2: (x₁,x₂)I

n=3: (x₁,x₂,x₃)I

AFD A accepta w ? <A,w> I ACC_AFD?

T a demonstra ca o problema de calculabilitate este rezolvabila algoritmic a demonstra ca un limbaj (asociat) este decidabil.

Teorema 1

Limbajul ACC_AFD= este decidabil.

Teorema 2

Limbajul ACC_AFN = este decidabil.

Teorema 3

Limbajul ACC_REX = este decidabil.

Observatie

T1, T2, T3

AFD AFN REX din punct de vedere al decidabilitatii limbajului recunoscut/generat

Teorema 4

Limbajul VID_AFD = este decidabil.

Teorema 5

Limbajul EQV_AFD = este decidabil.

Probleme decidabile in clasa limbajelor independente de context

Teorema 6

Limbajul ACC_GIC = este decidabil.

Lema 1

Fie GIGIC in forma normala Chomsky si wIL(G): |w|=n, nIN;

=> orice derivare a lui w in G are 2n-1 pasi.

Observatie

Teorema anterioara: GIC, APD: L(GIC)=L(APD).

T toate rezultatele demonstrate pentru gramaticile independente de context au loc si pentru automatele pushdown.

Teorema 7

Limbajul VID_GIC = este decidabil.

Observatie

Limbajul EQV_GIC = :

Cf. Teoremei 5, problema egalitatii limbajelor generate de gramatici REGULATE este decidabila

EQV_GIC = NU este decidabil.

Teorema 8

Orice limbaj independent de context este decidabil.

CURS 6

Problema opririi

1. Metoda diagonalizarii
2. Nedecidabilitatea unui limbaj dat
3. Un limbaj care nu este Turing-recunoscut

Definitia 1

Multimea A se n. numarabila

A este finita sau

f: N A, bijectiva.

Exemple de multimi numarabile

1. N' =
2. T =
3. Enumerarea lui Cantor

Multimile N² si N au aceeasi cardinalitate (1874)

functia J este bijectiva;

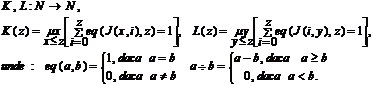inversele ei sunt:

J(x,y) = numarul lui Cantor asociat perechii (x,y);

Tripletul (J,K,L):

J(K(z),L(z))=z;K(J(x,y))=x,L(J(x,y))=y

triplet de functii pereche

Contraexemplu

R

4. Q = este numarabila

Utilizam tehnica diagonalizarii

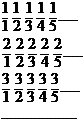Construim o matrice:

=> numarul rational m/n: celula aflata la intersectia liniei m cu coloana n.

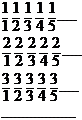
eliminam repetitiile =>

=> Limbaje care nu sunt decidabile si nici macar Turing recunoscute.

? multimea limbajelor este nenumarabila,

multimea MT este numarabila,

o MT poate recunoaste 1! limbaj.

Propozitia 1

L a*: L L(M), MIMT

demonstratie

(i) MT = multimea masinilor Turing este numarabila

Observam ca multimea a* este numarabila, a

MIMT poate fi codificata peste un alfabet A convenabil ales.

eliminam wIA*: w <M>, MIMT

obtinem o enumerare a MT.

(ii) multimea B a secventelor binare infinite este nenumarabila

Folosim metoda diagonalizarii

ppa f:N B, bijectiva a.i. f(n)=b_nIB

b=00111..

b f(n), nIN :

a n^a cifra binara din b este:

0, daca a n-a cifra binara din f(n) este 1;

1, daca a n-a cifra binara din f(n) este 0.

=> B este nenumarabila.

(iii) multimea L = este nenumarabila

E suficient sa gasim f: L B, bijectiva.

Fie a*=; L l_L infinita, unica, definita astfel:

cel de-al i-lea bit din l_L este: 1, daca s_iIL,

0, daca s_iÏL.

Exemplu: a=, L=

=> a

L

=> l_L= 0 1 0 1 1 0 0 1 1 1 1 0...

=> f: L B: f(L)= l_L

Evident: f = bijectiva.

cf. (ii) B =nenumarabila => L nenumarabila.

Din (i) si (ii) => exista limbaje care nu sunt Turing-recunoscute

Nedecidabilitatea unui limbaj dat

O MT, M, accepta sau nu o anumita secventa de intrare, w?

PROBLEMA ACCEPTABILITATII pt. LIMBAJE RECURSIV ENUMERABILE

PROBLEMA OPRIRII

ACC_MT=

Teorema 1

Limbajul ACC_MT= nu este decidabil.

Observatia 1

Lb ACC_MT este Turing-recunoscut dar nu este Turing-decidabil:

U = "Fie secventa de intrare <M,w>, unde MIMT si wIa

1. Se simuleaza M pe intrarea w.

2. Daca M accepta w, atunci U accepta <M,w>;

daca M respinge w, atunci U respinge <M,w>."

==> U recunoaste limbajul ACC_MT dar nu decide asupra lui:

M cicleaza pe w U cicleaza pe <M,w>.

? M nu se opreste pe w U respinge <M,w>

ACC_MT= decidabil

Observatia 2

Problema acceptabilitatii pt MT, ACC_MT, se n. si PROBLEMA OPRIRII tocmai datorita acestui fapt.

Observatia 3

U = exemplu de MT universala

O MT oarecare se numeste universala

ea poate simula orice MT, cu conditia sa primeasca la intrare o descriere corecta a acesteia.

Observatia 4

Teorema 1: MT acceptoare sunt mai puternice decat MT decidente.

demonstratie (T1)

Ppa ca limbajul ACC_MT este decidabil T

H = "Fie secventa de intrare <M,w>, unde M IMT si wIa

1. Se simuleaza M pe intrarea w.

2. Daca M accepta w, atunci H se opreste si accepta <M,w>;

daca M nu accepta w, atunci H se opreste si respinge <M,w>."

D apeleaza H pentru a determina ce actiune executa M atunci cand primeste, ca secventa de intrare w , propria sa descriere <M>;

dupa ce D a obtinut aceasta informatie ea executa exact actiunea contrara, i.e.:

D = "Fie secventa de intrare <M> , unde MIMT:

1. Se ruleaza H pe secventa de intrare <M,<M>>.

2. Se returneaza rezultatul opus rezultatului returnat de H, adica,

daca H accepta intrarea <M,<M>> (ceea ce se intampla atunci cand M accepta <M>) atunci D respinge;

daca H respinge intrarea <M,<M>> (ceea ce se intampla atunci cand M nu accepta <M>) atunci D accepta <M>."

Dar MT M din secventa de intrare este oarecare: ce se intampla cand D primeste la intrare propria sa descriere <D>?

respinge, daca D accepta <D>.

T D(<D>) =

accepta, daca D nu accepta <D>,

T contradictie

T nici D nici H nu pot exista in realitate

T limbajul ACC_MT nu este decidabil.

Fie multimea tuturor masinilor Turing, MT:

acc, daca M_i accepta intrarea <M_j>,

i.e.: celula (i,j)=

V, daca M_i nu accepta intrarea <M_j> (respinge sau cicleaza)

i.e.: celula (i,j)= rezultatul returnat de H pe intrarea <M_i,<Mj>>.

Un limbaj care nu este Turing-recunoscut

Definitia 2

Limbajul L S se numeste co-Turing-recunoscut

L' a*, L' = Turing-recunoscut astfel incat L' = a* L.

Teorema 2

L S*: L este decidabil

L este Turing-recunoscut si co-Turing-recunoscut.

demonstratie " T

ip: L este decidabil T L este Turing-recunoscut.

dar: L este decidabil T L este decidabil

T L este Turing-recunoscut T L este co-Turing-recunoscut (cf. def.).

"

ip: L este Turing-recunoscut si co-Turing-recunoscut

T L si L sunt Turing-recunoscute (cf. def.)

T M₁,M₂IMT: L=L(M₁), L =L(M₂).

Definim MT, M, astfel :

M = "Fie cuvantul de intrare w I S

1. Se ruleaza M₁ si M₂ in paralel pe intrarea w.

2. Daca M₁ accepta w atunci M accepta w iar daca M₂ accepta w atunci M respinge w."

Rularea in paralel a celor doua MT M₁ si M₂ : inzestrarea lui M cu 2 benzi de lucru.

Simularea se face alternativ: M simuleaza cate un pas al fiecarei masini pana cand una dintre ele se opreste.

M decide asupra limbajului L:

fie un cuvant oarecare w I S T w I L sau w I L

T fie M₁ fie M₂ accepta intrarea w.

Dar, conform definitiei sale, M se opreste oridecateori M₁ sau M₂ accepta cuvantul de intrare primit.

In plus, M accepta toate secventele din L si respinge toate secventele din L

T M decide asupra limbajului L T L este decidabil.

Corolarul 1

Limbajul NU este Turing-recunoscut.

demonstratie

Ppa: limbajul este Turing-recunoscut

Am dem ca limbajul ACC_MT este Turing-recunoscut

ACC_MT este decidabil (cf. Teorema 2) T contradictie cu Teorema 1.