Scopul fundamental al acestui capitol este:
De a furniza un set extins de exemple referitoare la utilizarea structurilor de date introduse in capitolul 1;
De a sublinia influenta profunda pe care adoptarea unei anumite structuri o are asupra algoritmului care o utilizeaza si asupra tehnicilor de programare care implementeaza algoritmul respectiv.
Sortarea este domeniul ideal al studiului:
Constructiei algoritmilor,
Al performantelor algoritmilor,
Al avantajelor si dezavantajelor unor algoritmi fata de altii in acceptiunea unei aplicatii concrete
Al tehnicilor de programare aferente difertitior algoritmi
Prin sortare se intelege in general ordonarea unei multimi de elemente, cu scopul de a facilita cautarea ulterioara a unui element dat.
Sortarea este o activitate fundamentala cu caracter universal.
Spre exemplu in cartea de telefoane, in dictionare, in depozitele de marfuri si in general in orice situatie in care trebuiesc cautate si regasite obiecte, sortarea este prezenta.
In cadrul acestui capitol se presupune ca sortarea se refera la anumite elemente care au o structura articol definita dupa cum urmeaza [1.a]:
TYPE TipElement = RECORD PRIVATE
cheie: integer; [1.a]
END;
Campul cheie precizat, poate fi neesential din punctul de vedere al informatiei inregistrate in articol, partea esentiala a informatiei fiind continuta in celelalte campuri.
Din punctul de vedere al sortarii insa, cheie este cel mai important camp intrucat este valabila urmatoarea definitie a sortarii.
o Fiind dat un sir de elemente apartinand tipul mai sus definit
a1, a2,.,an
o Prin sortare se intelege permutarea elementelor sirului intr-o anumita ordine:
ak1, ak2,..,akn
o Astfel incat sirul cheilor sa devina monoton crescator, cu alte cuvinte sa avem
ak1.cheie ak2.cheie akn.cheie
Tipul campului cheie se presupune a fi intreg pentru o intelegere mai facila, in realitate el poate fi insa orice tip scalar.
O metoda de sortare se spune ca este stabila daca dupa sortare, ordinea relativa a elementelor cu chei egale coincide cu cea initiala, element esential in special in cazul in care se executa sortarea dupa mai multe chei.
In cazul sortarii, dependenta dintre algoritmul care realizeaza sortarea si structura de date prelucrata este profunda.
Din acest motiv metodele de sortare sunt clasificate in doua mari categorii dupa cum elementele de sortat:
o Sunt inregistrate ca si tablouri in memoria centrala a sistemului de calcul ceea ce conduce la sortarea tablourilor numita sortare interna
o Sunt inregistrate intr-o memorie externa: ceea ce conduce la sortarea fisierelor (secventelor) numita si sortare externa.
Cerinta fundamentala care se formuleaza fata de metodele de sortare a tablourilor se refera la utilizarea cat mai economica a zonei de memorie disponibile.
Din acest motive pentru inceput, prezinta interes numai algoritmii care, dat fiind tabloul a, realizeaza sortarea 'in situ', adica chiar in zona de memorie alocata tabloului.
Pornind de la aceasta restrictie, in continuare algoritmii vor fi clasificati in functie de eficienta lor, respectiv in functie de timpul de executie pe care il necesita.
Aprecierea cantitativa a eficientei unui algoritm de sortare se realizeaza prin intermediul unor indicatori specifici.
Un astfel de indicator este numarul comparatiilor de chei notat cu C, pe care le executa algoritmul.
Un alt indicator este numarul de atribuiri de elemente, respectiv numarul de miscari de elemente executate de algoritm notat cu M.
Ambii indicatori depind de numarul total n al elementelor care trebuiesc sortate.
In cazul unor algoritmi de sortare simpli bazati pe asa-zisele metode directe de sortare atat C cat si M sunt proportionali cu n2 adica sunt O(n2).
Exista insa si metode avansate de sortare, care au o complexitate mult mai mare si in cazul carora indicatorii C si M sunt de ordinul lui n log n ( O(n log n)
Raportul n2/(n log n), care ilustreaza castigul de eficienta realizat de acesti algoritmi, este aproximativ egal cu 10 pentru n = 64, respectiv 100 pentru n = 1000.
Cu toate ca ameliorarea este substantiala, metodele de sortare directe prezinta interes din urmatoarele motive:
Sunt foarte potrivite pentru explicitarea principiilor majore ale sortarii.
Procedurile care le implementeaza sunt scurte si relativ usor de inteles.
Desi metodele avansate necesita mai putine operatii, aceste operatii sunt mult mai complexe in detaliile lor, respectiv metodele directe se dovedesc a fi superioare celor avansate pentru valori mici ale lui n.
Reprezinta punctul de pornire pentru metodele de sortare avansate.
Metodele de sortare care realizeaza sortarea 'in situ' se pot clasifica in trei mai categorii:
Sortarea prin insertie;
Sortarea prin selectie;
Sprin interschimbare.
In prezentarea acestor metode se va lucra cu tipul element definit anterior, precum si cu urmatoarele notatii [2.a].
TYPE TipIndice = 0..n;
TipTablou = ARRAY [TipIndice] OF TipElement;
VAR a: TipTablou; temp: TipElement; [2.a]
Aceasta metoda este larg utilizata de jucatorii de carti.
Elementele (cartile) sunt in mod conceptual divizate intr-o secventa destinatie a1ai-1 si intr-o secventa sursa ai.an.
In fiecare pas incepand cu i = 2 , elementul i al tabloului (care este de fapt primul element al secventei sursa), este luat si transferat in secventa destinatie prin inserarea sa la locul potrivit.
Se incrementeaza i si se reia ciclul.
Astfel la inceput se sorteaza primele doua elemente, apoi primele trei elemente si asa mai departe.
Se face precizarea ca in pasul i, primele i-l elemente sunt deja sortate, astfel incat sortarea consta numai in a insera elementul a[i] la locul potrivit intr-o secventa deja sortata.
In termeni formali, acest algoritm este precizat in secventa [2.1.a].
-------- ----- ------ ----- ----- ----- ----- ------
FOR i := 2 TO n DO
BEGIN [2.1.a]
temp:=a[i];
*insereaza x la locul potrivit in a[1]a[i]}
END;
Selectarea locului in care trebuie inserat a[i] se face parcurgand secventa destinatie deja sortata a[1],,a[i-1] de la dreapta la stanga,
Oprirea se realizeaza pe primul element a[j] care are cheia mai mica sau egala cu a[i],
Daca un astfel de element a[j] nu exista, oprirea se realizeaza pe a[1] adica pe prima pozitie.
Simultan cu parcurgerea, se realizeaza si deplasarea spre dreapta cu o pozitie a fiecarui element testat pana in momentul indeplinirii conditiei de oprire.
Acest caz tipic de repetitie cu doua conditii de terminare readuce in atentie metoda fanionului (&1.4.2.1).
Pentru aplicarea ei se introduce elementul auxiliar a[0] care se asigneaza initial cu a[i].
In felul acesta, cel mai tarziu pentru j = 0, conditia de a avea cheia lui a[j] 'mai mica sau egala' cu cheia lui a[i] se gaseste indeplinita.
Insertia propriu-zisa se realizeaza pe pozitia j+1.
Algoritmul care implementeaza sortarea prin insertie apare in [2.1.b] iar profilul sau temporal in figura 2.1.a.
PROCEDURE SortarePrinInsertie;
VAR i,j: TipIndice; temp: TipElement;
BEGIN
FOR i:= 2 TO n DO
BEGIN
temp:= a[i]; a[0]:= temp; j:= i‑1;
WHILE a[j].cheie>temp.cheie DO
BEGIN
a[j+1]:= a[j]; j:= j‑1 [2.1.b]
END;
a[j+1]:= temp
END
END
 SortarePrinInsertie
SortarePrinInsertie
FOR (n -1 iteratii)
2 atribuiri O(1)
WHILE (n -1 iteratii) O((n-1) n) = O(n O(n
1 comparatie
1 atribuire O(n-1) = O(n)
1 atribuire O(1)
Fig.2.1.a. Profilul temporal al algoritmului de sortare prin insertie
Dupa cum se observa, algoritmul de sortare contine un ciclu exterior dupa i care se reia de n-1 ori (bucla FOR).
In cadrul fiecarui ciclu exterior se executa un ciclu interior de lungime variabila dupa j, pana la indeplinirea conditiei (bucla WHILE).
In pasul i al ciclului exterior FOR , numarul minim de reluari ale ciclului interior este 0 iar numarul maxim de reluari este i-1 .
Analiza sortarii prin insertie
In cadrul celui de-al i-lea ciclu FOR, numarul Ci al comparatiilor de chei executate in bucla WHILE, depinde de ordinea initiala a cheilor, fiind:
Cel putin 1 (secventa ordonata),
Cel mult i-l (secventa ordonata invers)
In medie i/2, presupunand ca toate permutarile celor n chei sunt egal posibile
Intrucat avem n-1 reluari ale lui FOR pentru i:= 2..n , parametrul C are valorile precizate in [2.1.c].
![]()
![]()
![]()
Numarul maxim de atribuiri de elemente in cadrul unui ciclu FOR este C i + 3 si corespunde numarului maxim de comparatii
Explicatia: la numarul C i de atribuiri executate in cadrul ciclului interior WHILE de tip a[j+1]:= a[j]) se mai adauga 3 atribuiri (temp:= a[i], a[0]:= temp si a[i+1]:= temp).
Chiar pentru numarul minim de comparatii de chei (C i egal cu 1) cele trei atribuiri raman valabile.
In consecinta, parametrul M ia urmatoarele valori [2.1.d].
![]()
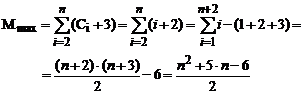
![]()
Se observa ca atat C cat si M sunt de ordinul lui n2 (O(n2)).
Valorile minime ale indicatorilor rezulta cand a este ordonat, iar valorile maxime, cand a este ordonat invers.
Sortarea prin insertie este o sortare stabila.
In secventa [2.1.e] se prezinta o varianta C a acestei metode de sortare cu fanionul pozitionat pe pozitia n.
// Sortarea prin insertie - varianta C
insertie(int a[],int n)
a[j-1]=a[n];
Algoritmul de sortare prin insertie poate fi imbunatatit pornind de la observatia ca secventa destinatie este deja sortata.
In acest caz cautarea locului de insertie se poate face mult mai rapid utilizand tehnica cautarii binare, prin impartiri succesive in parti egale a intervalului de cautare.
Algoritmul modificat se numeste insertie binara [2.1.f].
PRIVATE PROCEDURE SortarePrinInsertieBinara;
VAR i,j,stanga,dreapta,m: TipIndice; temp: TipElement;
a: TipTablou;
BEGIN
FOR i:= 2 TO n DO
BEGIN
temp:= a[i]; stanga:= 1; dreapta:= i‑1;
WHILE stanga<=dreapta DO
BEGIN [2.1.f]
m:= (stanga+dreapta)DIV 2;
IF a[m].cheie>temp.cheie THEN
dreapta:= m‑1
ELSE
stanga:= m+1
END;
FOR j:= i‑1 DOWNTO stanga DO a[j+1]:= a[j];
a[stanga]:= temp
END
END
Analiza insertiei binare
Pozitia de inserat este gasita daca
a[j].cheie x.cheie a[j+1].cheie ,
adica intervalul de cautare ajunge de dimensiune 1.
Daca intervalul initial este de lungime i sunt necesari log (i) pasi pentru determinarea locului insertiei.
Intrucat procesul de sortare presupune parcurgerea prin metoda injumatatirii binare a unor secvente de lungime i (care contin i chei), pentru i=1,2,,n , numarul total de comparatii C efectuate in bucla WHILE este cel evidentiat de expresia prezentata in [2.1.g].
![]()
Aceasta suma se poate aproxima prin integrala:
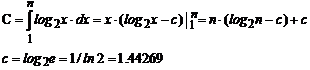
Numarul comparatiilor de chei este in principiu independent de ordinea initiala a cheilor.
De fapt numarul minim de comparatii, este necesar pentru un sir ordonat invers, iar numarul maxim pentru un sir ordonat.
Acesta este un caz de comportament anormal al unui algoritm de sortare.
Din nefericire beneficiile cautarii binare se rasfrang numai asupra numarului de comparatii si nu asupra numarului de miscari.
De regula, mutarea cheilor si a informatiilor asociate necesita mai mult timp decat compararea a doua chei,
Astfel intrucat M ramane de ordinul lui n2, performantele acestei metode de sortare nu cresc in masura in care ar fi de asteptat.
De fapt, resortarea unui tablou gata sortat, utilizand insertia binara, consuma mai mult timp decat insertia cu cautare secventiala.
In ultima instanta, sortarea prin insertie nu este o metoda potrivita de sortare cu ajutorul calculatorului, deoarece insertia unui element presupune deplasarea cu o pozitie in tablou a unui sir de elemente, deplasare care este neeconomica.
Acest dezavantaj conduce la ideea dezvoltarii unor algoritmi in care miscarile sa afecteze un numar mai redus de elemente si sa se realizeze pe distante mai mari.
Sortarea prin selectie rezolva aceste probleme.
Sortarea prin selectie foloseste procedeul de a selecta elementul cu cheia minima si de a schimba intre ele pozitia acestui element cu cea a primului element.
Se repeta acest procedeu cu cele n -1 elemente ramase, apoi cu cele n -2, etc., terminand cu ultimele doua elemente.
Aceasta metoda este oarecum opusa sortarii prin insertie care presupune la fiecare pas un singur element al secventei sursa si toate elementele secventei destinatie in care se cauta de fapt locul de insertie.
Selectia in schimb presupune toate elementele secventei sursa dintre care selecteaza pe cel cu cheia cea mai mica si il depoziteaza ca element urmator al secventei destinatie.
FOR i:= 1 TO n‑1 DO [2.2.a]
BEGIN
*gaseste cel mai mic element al lui a[i]a[n] si
asigneaza pe min cu indicele lui;
*interschimba pe a[i] cu a[min]
END;
In urma procesului de detaliere rezulta algoritmul prezentat in [2.2.b] al carui profil temporal apare in figura 2.2.a.
PROCEDURE SortarePrinSelectie;
VAR i,j,min: TipIndice; temp: TipElement;
a: TipTablou;
BEGIN
FOR i:= 1 TO n‑1 DO
BEGIN
min:= i; temp:= a[i];
FOR j:= i+1 TO n DO
IF a[j].cheie<temp.cheie THEN [2.2.b]
BEGIN
min:= j; temp:= a[j]
END;
a[min]:= a[i]; a[i]:= temp
END
END

SortarePrinSelectie

FOR (n -1 iteratii)
![]()
1 atribuire

FOR (i -1 iteratii)
Hm -1 atribuiri
1 comparatie
![]()
1 atribuire
![]()
2 atribuiri
Fig.2.2.a. Profilul temporal al sortarii prin selectie
Analiza sortarii prin selectie
Numarul comparatiilor de chei C este independent de ordinea initiala a cheilor.
![]()
Numarul atribuirilor este de cel putin 3 pentru fiecare valoare a lui i, (temp:= a[i],a[min]:= a[i],a[i]:= temp), de unde rezulta:
![]()
Acest minim poate fi atins efectiv, daca initial cheile sunt deja sortate.
Pe de alta parte daca cheile sunt initial in ordine inversa Mmax se determina cu ajutorul formulei empirice [2.2.e] [Wi76].
Valoarea medie a lui M nu este media aritmetica a lui Mmin si Mmax , ea obtinandu-se printr-un rationament probabilistic in felul urmator.
Se considera o secventa de m chei.
Fie o permutare oarecare a celor m chei notata cu k1 , k2 , , km.
Se determina numarul termenilor kj avand proprietatea de a fi mai mici decat toti termenii precedenti k1 , k2 , ,.kj-1.
Se aduna toate valorile obtinute pentru cele m! permutari posibile si se imparte suma la m!
Se demonstreaza ca rezultatul acestui calcul este Hm-1, unde Hm este suma partiala a seriei armonice [2.2.f][Wi76]:
![]()
Aceasta valoare reprezinta media numarului de atribuiri ale lui temp, executate pentru o secventa de m elemente, deoarece temp se atribuie ori de cate ori se gaseste un element mai mic decat toate elementele care-l preced.
Tinand cont si de atribuirile temp:=a[i],a[min]:=a[i] si a[i]:=temp, valoarea medie a numarului total de atribuiri pentru m termeni este Hm+2.
Se demonstreaza ca desi seria este divergenta, o suma partiala a sa se poate calcula cu ajutorul formulei [2.2.g]:
![]()
unde g = 0.5772156649... este constanta lui Euler [Kn76].
Pentru un m suficient de mare valoarea lui Hm se poate aproxima prin expresia:
![]()
Intrucat in procesul de sortare se parcurg succesiv secvente care au respectiv lungimea m = n , n-1 , n-2 ,, 1, fiecare dintre ele necesitand in medie Hm+2 atribuiri, numarul mediu total de atribuiri Mmed va avea expresia:
![]()
Suma de termeni discreti, poate fi aproximata cu ajutorul calculului integral [2.2.j]
![]()
aproximare care conduce la rezultatul:
![]()
In concluzie, algoritmul bazat pe selectie este de preferat celui bazat pe insertie, cu toate ca in cazurile in care cheile sunt ordonate, sau aproape ordonate, sortarea prin insertie este mai rapida.
Optimizarea performantei sortarii prin selectie poate fi realizata prin reducerea numarului de miscari de elemente ale tabloului.
In [Se88] se propune o astfel de varianta in care in loc de a memora de fiecare data elementul minim curent in variabila temp, se retine doar indicele acestuia, mutarea urmand a se realiza doar pentru ultimul element gasit, la parasirea ciclului FOR interior [2.2.k].
PROCEDURE SelectieOptimizata;
VAR i,j,min: TipIndice; temp: TipElement;
a: TipTablou;
BEGIN
FOR i:= 1 TO n‑1 DO [2.2.k]
BEGIN
min:= i;
FOR j:= i+1 TO n DO
IF a[j].cheie<temp.cheie THEN min:= j;
temp:= a[min]; a[min]:= a[i]; a[i]:= temp
END
END
Masuratorile experimentale efectuate insa asupra acestei variante nu evidentiaza vreo ameliorare nici chiar pentru valori mari ale dimensiunii tabloului de sortat.
Explicatia rezida in faptul ca atribuirile care necesita in plus accesul la componenta unui tablou se realizeaza practic in acelasi timp ca si o atribuire normala.
Clasificarea metodelor de sortare in diferite familii ca insertie, interschimbare sau selectie nu este intotdeauna foarte bine definita.
Paragrafele anterioare au analizat algoritmi care desi implementeaza insertia sau selectia, se bazeaza pe fapt pe interschimbare.
In acest paragraf se prezinta o metoda de sortare in care interschimbarea a doua elemente este caracteristica dominanta.
Principiul de baza al acestei metode este urmatorul: se compara si se interschimba perechile de elemente alaturate, pana cand toate elementele sunt sortate.
Ca si la celelalte metode, se realizeaza treceri repetate prin tablou, de la capat spre inceput, de fiecare data deplasand cel mai mic element al multimii ramase spre capatul din stanga al tabloului.
Daca se considera tabloul in pozitie verticala si se asimileaza elementele sale cu niste bule de aer in interiorul unui lichid, fiecare bula avand o greutate proportionala cu valoarea cheii, atunci fiecare trecere prin tablou se soldeaza cu ascensiunea unei bule la nivelul specific de greutate.
Din acest motiv aceasta metoda de sortare este cunoscuta in literatura sub denumirea de bubblesort (sortare prin metoda bulelor).
Algoritmul aferent acestei metode apare in continuare [2.a]:
PROCEDURE Bubblesort;
VAR i,j: TipIndice; temp: TipElement;
BEGIN
FOR i:= 2 TO n DO
BEGIN [2.a]
FOR j:= n DOWNTO i DO
IF a[j‑1].cheie>a[j].cheie THEN
BEGIN
temp:= a[j‑1]; a[j‑1]:= a[j]; a[j]:= temp
END
END
END
Profilul temporal al algoritmului de sortare prin interschimbare este prezentat in figura 2.a si el conduce la o estimare a incadrarii performantei algoritmului in ordinul O(n2).

Bubblesort

FOR (n - 1 iteratii)

FOR (i - 1 iteratii)
O(n
1 comparatie O(n) O(n n) = O(n
![]()
3 atribuiri
Fig.2.a. Profilul temporal al sortarii prin interschimbare
In multe cazuri ordonarea se termina inainte de a se parcurge toate iteratiile buclei FOR exterioare.
In acest caz, restul iteratiilor sunt fara efect, deoarece elementele sunt deja ordonate.
O modalitate evidenta de imbunatatire a algoritmului bazata pe aceasta observatie este aceea prin care se memoreaza daca a avut sau nu loc vreo interschimbare in cursul unei treceri.
Si in acest caz este insa necesara o ultima trecere, fara nici o interschimbare care marcheaza finalizarea algoritmului.
PROCEDURE Bubblesort1;
VAR i: TipIndice; modificat: boolean;
temp: TipElement;
BEGIN
REPEAT
modificat:= false;
FOR i:= 1 TO n-1 DO
IF a[i].cheie>a[i+1].cheie THEN [2.b]
BEGIN
temp:= a[i]; a[i]:= a[i+1]; a[i+1]:= temp;
modificat:= true
END
UNTIL NOT modificat
END
Un element usor plasat la capatul greu al tabloului este readus la locul sau intr-o singura trecere,
In schimb un element greu plasat la capatul usor al tabloului va fi readus spre locul sau doar cu cate o pozitie la fiecare trecere.
va fi sortat cu ajutorul metodei bubblesort imbunatatite intr-o singura trecere,
va necesita sapte treceri in vederea sortarii.
PROCEDURE Shakersort;
VAR j,ultim,stanga,dreapta: TipIndice;
temp: TipElement;
BEGIN
stanga:= 2; dreapta:= n; ultim:= n;
REPEAT
FOR j:= dreapta DOWNTO stanga DO [2.c]
IF a[j‑1].cheie>a[j].cheie THEN
BEGIN
temp:= a[j‑1]; a[j‑1]:= a[j]; a[j]:= temp;
ultim:= j
END;
stanga:= ultim+1;
FOR j:=stanga TO dreapta DO
IF a[j‑1].cheie>a[j].cheie THEN
BEGIN
temp:=a[j‑1]; a[j‑1]:=a[j]; a[j]:=temp;
ultim:=j
END;
dreapta:=ultim‑1
UNTIL (stanga>dreapta)
END
![]()
![]()
![]()
![]()
![]()
34 65 12 22 83 18 04 67
![]() sortare-4
sortare-4
![]()
![]() sortare-2
sortare-2
04 18 12 22 34 65 83 67
![]()
sortare-1
04 12 18 22 34 65 67 83
Fig. 2.4. Sortare prin insertie cu diminuarea incrementului
h , h2 , , ht , unde ht = 1, hi > hi+1 si 1 i < t [2.4.a]
PROCEDURE Shellsort;
CONST t=4;
VAR i,j,pas,s: TipIndice; temp: TipElement;
m: 1..t;
h: ARRAY[1..t] OF integer;
BEGIN
h[1]:= 9; h[2]:= 5; h[3]:= 3; h[4]:= 1;
FOR m:= 1 TO t DO
BEGIN
pas:= h[m]; s:= ‑pas;
FOR i:= pas+1 TO n DO
BEGIN
temp:= a[i]; j:= i‑pas;
IF s=0 THEN s:= ‑pas;
s:= s+1; a[s]:= temp; [2.4.b]
WHILE temp.cheie<a[j].cheie DO
BEGIN
a[j+k]:= a[j]; j:= j‑pas
END;
a[j+k]:= temp
END
END
END
1, 4, 13, 40, 121,
h t , h t-1 , , h k , h k-1 , , h1 [2.4.c]
unde h k-1
= 3 h k
+1 , h t
= 1 si t =
![]()
l, 3, 7, 15, 3l, [2.4.d]
unde h k-1
= 2 h k
+1 , h t
= 1 si t =
![]()
PROCEDURE Shellsort1;
VAR i,j,h: TipIndice; temp: TipElement;
BEGIN
h:= 1;
REPEAT h:= 3*h+1 UNTIL h>n;
REPEAT
h:= h DIV 3;
FOR i:= h+1 TO n DO [2.4.e]
BEGIN
temp:= a[i]; j:= i;
WHILE (a[j-h].cheie>temp.cheie) AND (j>h) DO
BEGIN
a[j]:= a[j-h]; j:= j-h
END;
a[j]:= temp
END;
UNTIL h=1
END
![]()
![]()
12 04
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Fig.2.5.a. Arbore de selectii
![]()
![]()
![]()
![]() 12
12
![]()
![]()
![]()
![]()
![]() 34 12 18
34 12 18
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 34 65 12 22 83 18 67
34 65 12 22 83 18 67
Fig. 2.5.b. Selectia celei mai mici chei
![]() 12
12
![]()
12 18
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 34 65 12 22 83 18 67
34 65 12 22 83 18 67
Fig. 2.5.c. Completarea locurilor libere
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() h1
h1
![]()
h2 h3
![]()
![]()
![]()
![]()
h4 h5 h6 h7
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
h8 h9 h10 h11 h12 h13 h14 h15
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
Fig. 2.5.d. Reprezentarea unui ansamblu printr-un tablou liniar h
Se presupune un ansamblu hs+1 , hs+2 , ., hd definit prin indicii s +1 si d
Acestui ansamblu i se adauga la stanga, pe pozitia hs un nou element x , obtinandu-se un ansamblu extins spre stanga hs , , hd .
![]()
![]() h1 04
h1 04
![]()
![]()
![]()
![]()
![]() 22 04 22 12
22 04 22 12
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
04 65 83 18 12 12 65 83 18 34
![]()
![]()
(a) (b)
Fig. 2.5.e. Deplasarea unei chei intr-un ansamblu
In figura 2.5.e.(a) apare ca exemplu ansamblul h2 , ., h7 , iar in aceeasi figura (b), ansamblul extins spre stanga cu un element x = 34 .
Deplasarea unei chei de sus in jos intr-un ansamblu - varianta pseudocod
procedure Deplasare(s,d: TipIndice)
i:= s;
temp:= h[i]
![]() cat timp exista niveluri
in ansamblu (j i) si
locul de
cat timp exista niveluri
in ansamblu (j i) si
locul de
plasare nu a fost gasit executa
selecteaza pe cel mai mic dintre fii elementului
indicat de i (pe h[j] sau pe h[j+1]
![]() daca temp>fiul_selectat
atunci
daca temp>fiul_selectat
atunci
deplaseaza fiul selectat in locul tatalui
sau (h[i]:=h[j]);
*avanseaza pe nivelul urmator al ansamblului
(i:=j; j:=2*i)
altfel [2.5.b]
retur
*plaseaza pe temp la locul sau in ansamblu
(h[i]:=temp);
Procedura Pascal care implementeaza algoritmul de deplasare apare in [2.5.c].
PROCEDURE Deplasare(s,d: TipIndice);
VAR i,j: TipIndice; temp: TipElement; ret: boolean;
BEGIN
i:= s; j:= 2*i; temp:= h[i]; ret:= false;
WHILE(j<=d) AND (NOT ret) DO
BEGIN
IF j<d THEN
IF h[j].cheie>h[j+1].cheie THEN j:= j+1;
IF temp.cheie>h[j].cheie THEN
BEGIN
h[i]:= h[j]; i:= j; j:= 2*i [2.5.c]
END
ELSE
ret:= true
END;
h[i]:= temp
END
R.W. Floyd a sugerat o metoda de a construi un ansamblu in situ, utilizand procedura de deplasare in ansamblu prezentata mai sus:
Se considera un tablou h1 , , hn in care in mod evident elementele hn/2 , , hn formeaza deja un ansamblu deoarece nu exista nici o pereche de indici i si j care sa satisfaca relatia j=2*i (sau j=2*i+1).
Aceste elemente formeaza cea ce poate fi considerat drept sirul de baza al ansamblului asociat.
In continuare, ansamblul este extins spre stanga, la fiecare pas cu cate un element, introdus in varf si deplasat pana la locul sau.
Prin urmare, considerand ca tabloul initial este memorat in h, procesul de generare 'in situ' al unui ansamblu poate fi descris prin secventa [2.5.d].
s:= (n DIV 2)+1;
WHILE s>1 DO
BEGIN [2.5.d]
s:= s‑1; Deplasare(s,n)
END;
In vederea sortarii elementelor, se executa n pasi de Deplasare, dupa fiecare pas selectandu-se varful ansamblului.
Problema care apare este aceea a locului in care se memoreaza varfurile consecutive ale ansamblului, respectiv elementele sortate, respectand constrangerea 'in situ'.
Aceasta problema poate fi rezolvata astfel:
In fiecare pas al procesului de sortare se interschimba ultima componenta a ansamblului cu componenta aflata in varful acestuia (h[1]).
Dupa fiecare astfel de interschimbare ansamblul se restrange la dreapta cu o componenta.
In continuare se lasa componenta din varf (h[1]) sa se deplaseze spre locul sau in ansamblu.
In termenii procedurii Deplasare aceasta tehnica poate fi descrisa ca in secventa [2.5.e].
d:= n;
WHILE d >1 DO
BEGIN
temp:= h[1]; h[1]:= h[d]; h[d]:= temp; [2.5.e]
d:= d‑1; Deplasare(1,d)
END;
Cheile se obtin sortate in ordine inversa, lucru care poate fi usor remediat modificand sensul relatiilor de comparatie din cadrul procedurii Deplasare.
Rezulta urmatorul algoritm care ilustreaza tehnica de sortare heapsort [2.5.f].
PROCEDURE Heapsort;
VAR s,d: TipIndice; temp: TipElement;
PROCEDURE Deplasare;
VAR i,j: TipIndice; ret: boolean;
BEGIN
i:=s; j:= 2*i; temp:= h[i]; ret:= false;
WHILE (j<=d) AND (NOT ret) DO
BEGIN
IF j<d THEN
IF h[j].cheie<h[j+1].cheie THEN j:= j+1;
IF temp.cheie<h[j] THEN
BEGIN
h[i]:= h[j]; i:= j; j:= 2*i
END
ELSE
ret:= true
END;
h[i]:= temp
END;
BEGIN
s:= (n DIV 2)+1; d:= n; [2.5.f]
WHILE s>1 DO
BEGIN
s:= s‑1; Deplasare
END;
WHILE d>1 DO
BEGIN
temp:= h[1]; h[1]:= h[d]; h[d]:= temp;
d:= d‑1; Deplasare
END
END
Analiza metodei heapsort.
La prima vedere nu rezulta in mod evident faptul ca aceasta metoda conduce la rezultate bune.
Analiza performantelor metodei heapsort contrazice insa aceasta parere.
La faza de constructie a ansamblului sunt necesari n/2 pasi de deplasare,
In fiecare fiecare pas se muta elemente de-a lungul a respectiv log(n/2) , log(n/2 +1) , , log(n-1) pozitii, (in cel mai defavorabil caz), unde logaritmul se ia in baza 2 si se trunchiaza la prima valoare intreaga.
In continuare, faza de sortare necesita n-1 deplasari cu cel mult log (n-2) , log (n-1) , , 1 miscari.
In plus mai sunt necesare 3 (n -1) miscari pentru a aseza elementele sortate in ordine.
Toate acestea dovedesc ca in cel mai defavorabil caz, tehnica heapsort are nevoie de un numar de pasi de ordinul O(n log n) [2.5.g].
O(n/2 log (n-1) + (n-1) log (n-1) + 3 (n-1)) = O(n log n) [2.5.g]
Este greu de determinat cazul cel mai defavorabil si cazul cel mai favorabil pentru aceasta metoda.
In general insa, tehnica heapsort este mai eficienta in cazurile in care elementele sunt intr-o mai mare masura sortate in ordine inversa; evident faza de creare a arborelui nu necesita nici o miscare daca elementele sunt chiar in ordine inversa.
Numarul mediu de miscari este aproximativ egal cu 1/2 n log n , deviatiile de la aceasta valoare fiind relativ mici.
In maniera specifica metodelor de sortare avansate, valorile mici ale numarului de elemente n, nu sunt suficient de reprezentative, eficienta metodei crescand o data cu cresterea lui n .
In secventa [2.5.h] se prezinta varianta C a algoritmului de sortare prin metoda ansamblelor.
sortare prin metoda ansamblelor - heapsort - varianta C
deplasare(int s,int d)
a[i-1]=x;
[2.5.h]
heapsort()
Desi metoda bubblesort bazata pe principiul interschimbarii este cea mai putin performanta dintre metodele studiate,
C.A.R. Hoare, pornind de la acelasi principiu, a conceput o metoda cu performante spectaculare pe care a denumit-o quicksort (sortare rapida).
Aceasta se bazeaza pe aceeasi idee de a creste eficienta interschimbarilor prin marirea distantei dintre elementele implicate.
Sortarea prin partitionare porneste de la urmatorul algoritm.
Fie x un element oarecare al tabloului de sortat a1 , , an .
Se parcurge tabloul de la stanga spre dreapta pana se gaseste primul element ai > x .
In continuare se parcurge tabloul de la dreapta spre stanga pana se gaseste primul element aj < x .
Se interschimba intre ele elementele ai si aj ,
Se continua parcurgerea tabloului de la stanga respectiv de la dreapta (din punctele in care s-a ajuns anterior), pana se gasesc alte doua elemente care se interschimba, s.a.m.d.
Procesul se termina cand cele doua parcurgeri se 'intalnesc' undeva in interiorul tabloului.
Efectul final este ca acum sirul initial este partitionat intr-o partitie stanga cu chei mai mici decat x si o partitie dreapta cu chei mai mari decat x.
Considerand elementele sirului memorate in tabloul a , principiul partitionarii apare prezentat sintetic in [2.6.a].
*Partitionarea unui tablou - varianta pseudocod
procedure Partitionare *selecteaza elementul x (de regula de la mijlocul
intervalului de partitionat)
![]() repeta
repeta
*cauta primul element a[i]>x, parcurgand
intervalul de la stanga la dreapta
*cauta primul element a[j]<x, parcurgand
intervalul de la dreapta la stanga
![]() daca i<=j atunci [2.6.a]
daca i<=j atunci [2.6.a]
*interschimba pe a[i] cu a[j]
pana cand parcurgerile se intalnesc (i>j)
Inainte de a trece la sortarea propriu-zisa, se da o formulare mai precisa partitionarii in forma unei proceduri [2.6.b].
Se precizeaza ca relatiile > respectiv < au fost inlocuite cu respectiv ale caror negate utilizate in instructiunile WHILE sunt < respectiv >.
In acest caz x joaca rol de fanion pentru ambele parcurgeri.
PROCEDURE Partitionare;
VAR x,temp: TipElement;
BEGIN
[1] i:= 1; j:= n;
[2] x:= a[n DIV 2]; [2.6.b]
[3] REPEAT
[4] WHILE a[i].cheie<x.cheie DO i:= i+1;
[5] WHILE a[j].cheie>x.cheie DO j:= j‑1;
[6] IF i<=j THEN
BEGIN
[7] temp:= a[i]; a[i]:= a[j]; a[j]:= temp;
[8] i:= i+1; j:= j‑1
END
[9] UNTIL i>j
END;
In continuare, cu ajutorul partitionarii, sortarea se realizeaza simplu:
Dupa o prima partitionare a secventei de elemente se aplica aceeasi procedura celor doua partitii rezultate,
Apoi celor patru partitii ale acestora, s.a.m.d.
Pana cand fiecare partitie se reduce la un singur element.
Tehnica sortarii bazata pe partitionare este ilustrata in secventa [2.6.c].
Sortarea prin partitionare -quicksort - varianta pseudocod
procedure QuickSort(s,d);
*partitioneaza intervalul s,d fata de Mijloc
daca exista partitie stanga atunci
QuickSort(s,Mijloc-1) [2.6.c]
daca exista partitie dreapta atunci
QuickSort(Mijloc+1,d);
In secventa [2.6.d] apare o implementare a sortarii Quicksort in varianta Pascal iar in secventa [2.6.e] varianta de implementare in limbajul C.
PROCEDURE Quicksort;
PROCEDURE Sortare(VAR s,d: TipIndice);
VAR i,j: TipIndice;
x,temp: TipElement;
BEGIN
i:= s; j:= d;
x:= a[(s+d) DIV 2];
REPEAT
WHILE a[i].cheie<x.cheie DO i:= i+1;
WHILE x.cheie<a[j].cheie DO j:= j‑1; [2.6.d]
IF i<=j THEN
BEGIN
temp:= a[i]; a[i]:= a[j]; a[j]:= temp;
i:= i+1; j:= j‑1
END
UNTIL i>j;
IF s<j THEN Sortare(s,j);
IF i<d THEN Sortare(i,d);
END;
BEGIN
Sortare(1,n)
END
//Sortarea prin partitionare - quicksort - varianta C
quicksort(int s,int d)
}while(i<=j);
if(s<j)quicksort(s,j);
if(d>i)quicksort(i,d);
In continuare se prezinta o maniera de implementare a aceluiasi algoritm utilizand o procedura nerecursiva.
Elementul cheie al solutiei iterative rezida in mentinerea unei liste a cererilor de partitionare.
Astfel, la fiecare trecere apar doua noi partitii.
Una dintre ele se prelucreaza imediat, cealalta se amana, prin memorarea ei ca cerere in lista.
In mod evident, lista de cereri trebuie rezolvata in sens invers, adica prima solicitare se va rezolva ultima si invers,
Cu alte cuvinte lista se trateaza ca o stiva.
In secventa [2.6.f ] apare o schita de principiu a acestei implementari in varianta pseudocod.
*Sortare QuickSort. Implementare nerecursiva - Varianta pseudocod
procedure QuickSortNerecursiv;
*se introduc in stiva limitele
intervalului initial
de sortare (amorsarea procesului)
![]() repeta
repeta
*se extrage intervalul din varful stivei care
devine IntervalCurent
*se reduce stiva cu o pozitie [2.6.f]
![]() repeta
repeta
![]() repeta
repeta
*se partitioneaza IntervalCurent
pana cand terminare partitionare
![]() daca
exista interval drept atunci
daca
exista interval drept atunci
*se introduc limitele sale in stiva
*se face intervalul stang IntervalCurent
pana cand intervalul ajunge de latime 1 sau 0
pana cand stiva se goleste
In procedura Pascal care implementeaza algoritmul din secventa anterioara,
O cerere de partitionare este reprezentata printr-o pereche de indici care delimiteaza zona de tablou ce urmeaza a fi partitionata.
Stiva este modelata cu ajutorul unui tablou cu dimensiunea variabila numit stiva si de un index is care precizeaza varful acesteia [2.6.g].
Dimensiunea maxima m a stivei va fi discutata pe parcursul analizei metodei.
PROCEDURE QuickSortNerecursiv;
CONST m = ;
VAR i,j,s,d: TipIndice;
x,temp: TipElement;
is: 0..m;
stiva: ARRAY[1..m] OF
RECORD
s,d: TipIndice
END;
BEGIN
is:= 1; stiva[1].s:= 1; stiva[1].d:= n;
REPEAT
s:= stiva[is].s; d:= stiva[is].d; is:= is‑1;
REPEAT
i:= s; j:= d; x:= a[(s+d) DIV 2];
REPEAT
WHILE a[i].cheie<x.cheie DO i:= i+1;
WHILE x.cheie<a[j].cheie DO j:= j‑1;
IF i<=j THEN [2.6.g]
BEGIN
temp:= a[i]; a[i]:= a[j]; a[j]:= temp;
i:= i+1; j:= j‑1
END
UNTIL i>j;
IF i<d THEN
BEGIN
is:= is+1; stiva[is].s:= i; stiva[is].d:= d
END;
d:= j
UNTIL s>=d
UNTIL is=0
END
Analiza metodei quicksort
Pentru a analiza performanta acestei metode, se analizeaza mai intai partitionarea.
Se presupune pentru simplificare,
(1) Ca setul ce va fi partitionat consta din n chei distincte si unice cu valorile
(2) Ca dintre cele n chei a fost selectata cheia cu valoarea x in vederea partitionarii.
In consecinta aceasta cheie ocupa a x-a pozitie in multimea ordonata a cheilor si ea poarta denumirea de pivot.
Se ridica urmatoarele intrebari:
Care este probabilitatea ca dupa ce a fost selectata cheia cu valoarea x ca pivot, o cheie oarecare a partitiei sa fie interschimbata ?
Pentru ca o cheie sa fie interschimbata ea trebuie sa fie mai mare ca x.
Sunt n-x+1 chei mai mari ca x
Rezulta ca probabilitatea ca o cheie oarecare sa fie interschimbata este (n - x + 1) / n (raportul dintre numarul de cazuri favorabile si numarul de cazuri posibile).
Care este numarul de interschimbari necesar la o partitionare a n chei pentru care s-a selectat ca pivot cheia situata pe pozitia x ?
La dreapta pivotului exista n - x pozitii care vor fi procesate in procesul de partitionare.
Numarul posibil de interschimbari in acest context este deci egal cu produsul dintre numarul de chei care vor fi selectate (n - x ) si probabilitatea ca o cheie selectata sa fie interschimbata.
![]()
![]()
Care este numarul mediu de interschimbari pentru partitionarea unei secvente de n chei?
La o partitionare poate fi selectata oricare din cele n chei ca si pivot, deci x poate lua orice valoare cuprinsa intre 1 si n.
Numarul mediu M de interschimbari pentru partitionarea unei secvente de n chei se obtine insumand toate numerele de interschimbari pentru toate valorile lui x cuprinse intre 1 si n si impartind la numarul total de chei n [2.6.h].
![]()
Presupunand in mod exagerat ca intotdeauna va fi selectata mediana partitiei (mijlocul sau valoric), fiecare partitionare va divide tabloul in doua jumatati egale.
Se face precizarea ca mediana este elementul situat ca si valoare in mijlocul partitiei, daca aceasta este ordonata.
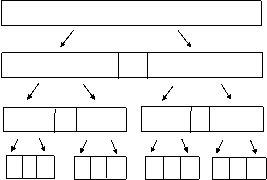
In aceste conditii este necesar un numar de treceri prin toate elementele tabloului egal cu log n (fig.2.6.a).
Dupa cum rezulta din figura 2.6.a, pentru un tablou de 15 elemente sunt necesare log = 4 treceri prin toate elementele tabloului sau 4 pasi de partitionare integrala a tabloului.
Numar apeluri Numar elemente de
partitionat pe apel
 1 apel
sortare
1 apel
sortare
(15 elemente) 15 elemente 15
2 apeluri sortare
(7 elemente) 7 elemente 1 7 elemente 7
4 apeluri sortare
(3 elemente) 3 elem 1 3 elem 3 elem 1 3 elem 3
8 apeluri sortare
(1 element)
Fig. 2.6.a. Functionarea principiala a sortarii prin partitionare
Din pacate numarul de apeluri recursive ale procedurii este egal cu 15, adica exact cu numarul de elemente.
Rezulta ca numarul total de comparatii este n log n (la o trecere sunt comparate toate cheile)
Numarul de miscari este n/6 log n deoarece conform formulei [2.6.h] la partitionarea a n chei sunt necesare in medie n/6 miscari [2.6.i].
![]()
Aceste rezultate sunt exceptional de bune, dar se refera numai la cazul optim in care s-a presupus ca la fiecare trecere se selecteaza mediana, eveniment care de altfel are probabilitatea doar 1/n.
Marele succes al algoritmului quicksort se datoreste insa faptului surprinzator ca performanta sa medie, la care alegerea pivotului se face la intamplare, este inferioara performantei optime doar cu un factor egal cu 2 1n deci cu aproximativ 40 % [Wi76].
Tehnica prezentata are insa si dezavantaje.
In primul rand ca si la toate metodele de sortare avansate, performantele ei sunt moderate pentru valori mici ale lui n.
Acest dezavantaj poate fi contracarat prin incorporarea unor metode de sortare directe pentru partitiile mici, lucru realizabil relativ simplu la aceasta metoda in raport cu alte metode avansate.
Un al doilea dezavantaj, se refera la cazul cel mai defavorabil in care performanta metodei scade catastrofal.
Acest caz apare cand la fiecare partitionare este selectata cea mai mare (cea mai mica) valoare ca si pivot.
Fiecare pas va partaja in acest caz secventa formata din n elemente, intr-o partitie stanga cu n - 1 elemente si o partitie dreapta cu un singur element.
Vor fi necesare astfel n partitionari in loc de log (n), iar performanta obtine valori de ordinul O(n2).
In mod aparent, elementul esential al acestei metode il reprezinta selectia pivotului x [GG78].
In exemplul prezentat, pivotul a fost ales la mijlocul partitiei.
El poate fi insa ales la extremitatea stanga sau dreapta a acesteia, situatie in care, cazul cel mai defavorabil il reprezinta partitia deja sortata.
Tehnica quicksort se comporta straniu:
Are performante slabe in cazul sortarilor banale
Are performante deosebite in cazul tablourilor dezordonate.
De asemenea, daca x se alege intotdeauna la mijloc (mediana), atunci tabloul sortat invers devine cazul optim al sortarii quicksort.
De fapt performanta medie este cea mai buna in cazul alegerii pivotului la mijlocul partitiei.
Hoare sugereaza ca alegerea sa se faca:
Fie la 'intamplare',
2) Fie prin selectia medianei unui numar redus de chei (spre exemplu trei chei).
O astfel de alegere judicioasa a pivotului influenteaza serios in mod negativ performanta medie a algoritmului quicksort, dar inbunatateste in mod considerabil performanta cazului cel mai defavorabil.
Pentru programator, in multe situatii cazul cel mai defavorabil are o influenta deosebita.
Spre exemplu in secventa [2.6.g] care implementeaza metoda quiqsort in maniera iterativa, in cazul cel mai defavorabil, la fiecare partitionare rezulta o partitie dreapta cu un singur element, a carei cerere de sortare se introduce in stiva.
Este evident ca in acest caz, dimensiunea maxima a stivei trebuie sa fie egala cu numarul de elemente n, situatie care nu este acceptabila.
Acest lucru este si mai grav in cazul recursivitatii unde stiva gestionata in mod automat este mult mai substantiala, fiind necesar cate un nod pentru fiecare apel recursiv, nod care presupune spatiu de memorie pentru stocarea valorilor parametrilor locali ai apelului la care se adauga de regula si codul efectiv al procedurii.
Aceasta situatie se rezolva, introducand in stiva cererea de sortare a partitiei mai mari si continuand cu partitionarea partitiei mai mici.
In acest caz dimensiunea m a stivei poate fi limitata la m = log 2 n .
Pentru a implementa aceasta tehnica, secventa [2.6.g] se modifica in portiunile in care se proceseaza cererile de partitionare conform [2.6.j].
IF j-s < d-i THEN
BEGIN
IF i<d THEN
BEGIN
is:= is+1; stiva[is].s:= i; stiva[is].d:= d
END;
d:= j
END
ELSE
BEGIN [2.6.j]
IF s<j THEN
BEGIN
s:= is+1; stiva[is].s:= s; stiva[is].d:= j
END;
s:= i
END;
Mediana a n elemente este definita ca fiind acel element care este mai mic (sau egal) decat jumatate din elemente si este mai mare (sau egal) decat cealalta jumatate.
o Spre exemplu mediana secventei 16, 12, 99, 95, 18, 87, 10 este 18 .
Problema aflarii medianei este corelata direct cu cea a sortarii deoarece, o metoda sigura de a determina mediana este urmatoarea:
o Se sorteaza cele n elemente
o Se extrage elementul din mijloc.
Tehnica partitionarii poate insa conduce la o metoda generala mai rapida, cu ajutorul careia se poate determina cel de-al k-lea element ca valoare dintre n elemente.
o Gasirea medianei reprezinta cazul special k = n / 2 .
o In acelasi context, k = 1 precizeaza aflarea minimului, iar k = n , aflarea maximului.
Algoritmul conceput de C.A.R. Hoare functioneaza dupa cum urmeaza.
o Se presupune ca elementele avute in vedere sunt memorate in tabloul a cu dimensiunea n,
o Pentru inceput se realizeaza o partitionare cu limitele s = 1, d = n si cu a[k] selectat pe post de pivot x.
o In urma acestei partitionari rezulta valorile index i si j care satisfac relatiile [2.7.a].
1) x = a[k]
2) a[h] x pentru toti h < i
3) a[h] x pentru toti h > j [2.7.a]
4) i > j
o Sunt posibile trei situatii:
Valoarea pivotului x a fost prea mica, astfel incat limita dintre cele doua partitii este sub valoarea dorita k. Procesul de partitionare trebuie continuat pentru elementele a[i],,a[d] (partitia dreapta) (fig.2.7.a (a)).
2. Valoarea pivotului x a fost prea mare. Operatia de partitionare continua pentru partitia a[s],,a[j] (partitia stanga) (fig.2.7.a (b)).
j < k < i . In acest caz elementul a[k] separa tabloul in doua partitii, el desemnand mediana (fig.2.7.a (c)).
o Procesul de partitionare se repeta pana la realizarea cazului
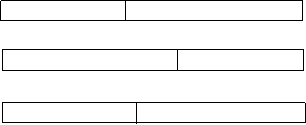
(a)
s j i k d
(b)
s k j i d
(c)
s j k i d
Fig. 2.7.a. Determinarea medianei
Algoritmul aferent este prezentat in varianta peseudocod in secventa [2.7.b] respectiv o prima rafinare in secventa de program [2.7.c].
procedure Mediana (s,d,k);
![]() cat timp exista
partitie [2.7.b]
cat timp exista
partitie [2.7.b]
*alege pivotul (elementul din pozitia k)
*partitioneaza intervalul curent fata de valoarea
pivotului
daca pozitie pivot<k atunci *selecteaza partitia
dreapta
daca pozitie pivot>k atunci *selecteaza partitia
stanga
s:= 1; d:= n ;
WHILE s<d DO
BEGIN
x:= a[k]; [2.7.c]
*se partitioneaza a[s]a[d]
IF j<k THEN s:= i;
IF k<i THEN d:= j
END;
Programul aferent apare in secventa [2.7.d] in varianta Pascal.
PROCEDURE Mediana (k:integer);
VAR s,d,i,j: TipIndice; x,temp: TipElement;
BEGIN
s:=1; d:=n;
WHILE s<d DO
BEGIN
x:= a[k]; i:= s; j:= d;
REPEAT [2.7.d]
WHILE a[i]<x DO i:= i+1;
WHILE x<a[j] DO j:= j-1;
IF i<=j DO
BEGIN
temp:= a[i]; a[i]:= a[j]; a[j]:= temp;
i:= i+1; j:= j‑1
END
UNTIL i>j;
IF j<k THEN s:= i;
IF k<i THEN d:= j
END
END;
Daca se presupune ca in medie fiecare partitionare injumatateste partitia in care se gaseste elementul cautat, atunci numarul necesar de comparatii C este de ordinul lui n [2.7.e].
![]()
Numarul de miscari M nu poate depasi numarul de comparatii, el fiind de regula mai mic.
Valorile indicatorilor C si M estimati pentru determinarea medianei subliniaza superioritatea acestei metode si explica performanta ei fata de metodele bazate pe sortarea tabloului si extragerea celui de-al k-lea element, a caror performanta in cel mai bun caz este de ordinul O(n log n)
In cel mai defavorabil caz, fiecare partitionare reduce setul de candidati numai cu 1, rezultand un numar de comparatii de ordinul O(n2). Si in acest caz metoda medianei este indicata pentru valori mari ale lui n (n > 10).
In general algoritmii de sortare bazati pe metode avansate au nevoie de O(n log n) pasi pentru a sorta n elemente.
Trebuie precizat insa faptul ca acest lucru este valabil in situatia in care nu exista nici o alta informatie suplimentara referitoare la chei, decat faptul ca pe multimea acestora este definita o relatie de ordonare, prin intermediul careia se poate preciza daca valoarea unei chei este mai mica respectiv mai mare decat o alta.
Dupa cum se va vedea in continuare, sortarea se poate face si mai rapid decat in limitele performantei O(n log n), daca:
o Exista si alte informatii referitoare la cheile care urmeaza a fi sortate
o Si se renunta macar partial la constrangerea de sortare 'in situ'.
Spre exemplu, se cere sa se sorteze un set de n chei de tip intreg, ale caror valori sunt unice si apartin intervalului de la 1 la n.
o In acest caz, daca a si b sunt tablouri identice cu cate n elemente, a continand cheile care urmeaza a fi sortate, atunci sortarea se poate realiza direct in tabloul b conform secventei [2.8.a].
FOR i:= 1 TO n DO
b[a[i].cheie]:= a[i]; [2.8.a]
o In secventa [2.8.a] se determina locul elementului a[i] si se plaseaza elementul la locul potrivit.
o Intregul ciclu necesita O(n) pasi.
o Rezultatul este insa corect numai in cazul in care exista un singur element cu cheia x, pentru fiecare valoare cuprinsa intre [1,n]. Un al doilea element cu aceeasi cheie va fi introdus tot in b[x] distrugand elementul anterior.
Acest tip de sortare poate fi realizat si 'in situ', element care prezinta interes din punctul de vedere al tehnicilor analizate.
o Astfel, fiind dat tabloul a de dimensiune n, ale carui elemente au respectiv cheile 1, , n, se baleeaza pe rand elementele sale.
o Daca elementul a[i] are cheia j, atunci se realizeaza interschimbarea lui a[i] cu a[j].
o Fiecare interschimbare plaseaza elementul aflat in locatia i exact la locul sau in tabloul ordonat, fiind necesare in cel mai rau caz 3 n miscari pentru intreg procesul de sortare.
o Secventa de program care ilustreaza aceasta tehnica apare in [2.8.b].
FOR i:= 1 TO n DO
WHILE a[i].cheie<>i DO
BEGIN [2.8.b]
temp:= a[i];a[i]:= a[a[i].cheie];
a[temp.cheie]:= temp
END;
Secventele [2.8.a, b] ilustreaza tehnica de sortare numita binsort, in cadrul careia se creaza bin-uri, fiecare bin pastrand un element sortat cu o anumita cheie [AHU85].
Tehnica sortarii este simpla:
o se examineaza fiecare element de sortat si se introduce in bin-ul corespunzator valorii cheii.
In secventa [2.8.a] bin-urile sunt chiar elementele tabloului b, unde b[i] este binul cheii avand valoarea i, iar in secventa [2.8.b] bin-urile sunt chiar elementele tabloului a dupa reasezare.
Tehnica aceasta atat de simpla si de performanta se bazeaza pe urmatoarele cerinte apriorice:
o (1) Domeniul limitat al cheilor (1, n)
o (2) Unicitatea fiecarei chei.
Daca cea de-a doua cerinta nu este respectata, si de fapt acesta este cazul obisnuit, este necesar ca intr-un bin sa fie memorate mai multe elemente avand aceeasi cheie.
Acest lucru se realizeaza fie prin insiruire, fie prin concatenare, fiind utilizate in acest scop structuri de date lista.
Aceasta situatie nu deterioreaza prea mult performantele acestei tehnici, efortul de sortare ajungand egal cu O(n+m), unde n este numarul de elemente iar m numarul de chei, motiv pentru care aceasta metoda reprezinta punctul de plecare al mai multor tehnici de sortare a structurilor lista [AHU85].
Spre exemplu, o metoda de rezolvare a unei astfel de situatii este cea bazata pe determinarea distributiei cheilor ('distribution counting') [Se88].
Problema se formuleaza astfel: se cere sa se sorteze un tablou cu n articole ale caror chei sunt cuprinse intre 0 si m-1.
Daca m nu este prea mare pentru rezolvarea problemei poate fi utilizat algoritmul de 'determinare a distributiei cheilor'. PRIVATE
Ideea algoritmului este:
o Se contorizeaza intr-o prima trecere numarul de chei pentru fiecare valoare de cheie care apare in tabloul a;
o Se ajusteaza valorile contoarelor;
o Intr-o a doua trecere, utilizand aceste contoare, se muta direct articolele in pozitia lor ordonata in tabloul b.
o Formularea algoritmului este cea din secventa [2.8.c]. Pentru simplificare se presupune ca tabloul a este un tablou care contine doar chei.
TYPE TipCheie = 0..m-1;
TipTablou = ARRAY [1..n] OF TipCheie;
VAR numar: ARRAY[0..m-1] OF TipCheie;
a,b: TipTablou;
i,j: TipIndice;
BEGIN
FOR j:= 1 TO m-1 DO numar[j]:= 0;
FOR i:= 1 TO n DO numar[a[i]]:= numar[a[i]]+1;
FOR j:= 1 TO m-1 DO numar[j]:= numar[j-1]+numar[j];
FOR i:=n DOWNTO 1 DO
BEGIN
b[numar[a[i]]]:= a[i]; [2.8.c]
numar[a[i]]:= numar[a[i]]-1
END;
FOR i:= 1 TO n DO a[i]:= b[i];
END
Contoarele asociate cheilor sunt memorate in tabloul numar de dimensiune m .
Initial locatiile sunt initializate pe zero (prima bucla FOR)
Sunt contorizate cheile (a doua bucla FOR).
In continuare sunt ajustate valorile contoarelor tabloului numar (a treia bucla FOR) astfel incat,
Parcurgand tabloul a de la sfarsit spre inceput, cheile sa poata fi introduse exact la locul lor in tabloul b cu ajutorul contoarelor memorate in tabloul numar (a patra bucla FOR).
Concomitent cu introducerea are loc si ajustarea contoarelor astfel incat cheile identice sa fie introduse in binul specific in ordinea relativa in care apar ele in secventa initiala.
Ultima bucla realizeaza mutarea integrala a elementelor tabloului b in tabloul a, daca acest lucru este necesar.
Desi se realizeaza mai multe treceri prin elementele tabloului totusi in ansamblu, performanta algoritmului este O(n) .
Aceasta metoda de sortare pe langa faptul ca este rapida are avantajul de a fi stabila, motiv pentru care ea sta la baza mai multor metode de sortare de tip radix.
In continuare se prezinta un exemplu de functionare a algoritmului de sortare bazat pe determinarea distributiei cheilor.
1) Se considera initial ca tabloul a are urmatorul continut:
|
a |
b |
b |
a |
c |
a |
D |
a |
b |
b |
a |
d |
d |
a |
2) Se initializeaza tabloul numar:
3) Se contorizeaza valorile cheilor tabloului a:
4) Se ajusteaza valorile tabloului numar
5) Se iau elementele tabloului a de la dreapta la stanga si se introduc pe rand in tabloul b, fiecare in pozitia indicata de contorul propriu din tabloul numar. Dupa introducerea fiecarui element in tabloul b, contorul specific din tabloul numar este decrementat cu o unitate.
|
a |
a |
a |
a |
a |
a |
b |
b |
b |
b |
c |
d |
d |
d |
Metodele de sortare prezentate pana in prezent, concep cheile de sortat ca entitati pe care le prelucreaza integral prin comparare sau interschimbare.
In unele situatii insa se poate profita de faptul ca aceste chei sunt de fapt numere apartinand unui domeniu marginit.
Metodele de sortare care iau in considerare proprietatile digitale ale numerelor sunt metodele de sortare bazate pe baze de numeratie ('radix sort').
Algoritmii de tip baza de numeratie, trateaza cheile ca si numere reprezentate intr-o baza de numeratie m, unde m poate lua diferite valori ('radix') si proceseaza cifrele individuale ale numarului.
Un exemplu sugestiv il reprezinta sortarea unui teanc de cartele care au perforate pe ele numere formate trei cifre.
o Se grupeaza cartelele in 10 grupe distincte, prima cuprinzand cheile mai mici decat 100, a doua cheile cuprinse intre 100 si 199, etc., adica se realizeaza o sortare dupa cifra sutelor.
o In continuare se sorteaza pe rand grupele formate aplicand aceeasi metoda, dupa cifra zecilor,
o Apoi fiecare grupa nou formata, dupa cifra unitatilor.
o Acesta este un exemplu simplu de sortare radix cu m = 10.
Pentru sistemele de calcul, unde prelucrarile se fac exclusiv in baza 2, se preteaza cel mai bine metodele de sortare radix care opereaza cu numere binare.
In general, in sortarea radix a unui set de numere, operatia fundamentala este extragerea unui set contiguu de biti din numarul care reprezinta cheia.
Spre exemplu pentru a extrage primii 2 biti ai unui numar binar format din 10 cifre binare:
o Se realizeaza o deplasare la dreapta cu 8 pozitii a reprezentarii numarului,
o Apoi se opereaza configuratia obtinuta, printr-o operatie 'si' cu masca 0000000011.
Aceste operatii pot fi implementate direct cu ajutorul facilitatilor de prelucrare a configuratiilor la nivel de biti puse la dispozitie de limbajele moderne de programare sau pot fi simulate cu ajutorul operatorilor intregi DIV si MOD.
o Spre exemplu, in situatia anterioara, daca x este numarul binar in cauza, primii doi biti se obtin prin expresia (x DIV 28)MOD 22.
In cadrul acestui paragraf, pentru exemplificarea sortarilor radix, se considera definita o functie biti(x,k,j:integer):integer care combina cele doua operatii returnand j biti care apar la k pozitii de la marginea dreapta a lui x.
O posibila implementare in limbajul C a acestei functii apare in secventa [2.9.a].
unsigned biti(unsigned x, int k, int j) [2.9.a]
Exista doua metode de baza pentru implementarea sortarii radix.
Prima metoda examineaza bitii cheilor de la stanga la dreapta si se numeste sortare radix prin interschimbare ('radix exchange sort').
o Ea se bazeaza pe faptul ca rezultatul comparatiei a doua chei este determinat de valoarea bitilor din prima pozitie la care ele difera.
o Astfel, elementele ale caror chei au primul bit 0 sunt trecute in fata celor care au primul bit 1;
o In continuare in fiecare grup astfel format se aplica aceeasi metoda pentru bitul urmator si asa mai departe.
o Sortarea propriu-zisa se realizeaza prin schimbarea sistematica a elementelor in maniera precizata.
A doua metoda se numeste sortare radix directa ('straight radix sort').
o Ea examineaza bitii din cadrul cheilor de la dreapta la stanga si se bazeaza pe principiul interesant care reduce sortarea cheilor de b-biti la b sortari ale unor chei de 1bit.
Se presupune ca se doreste sortarea elementelor tabloului a astfel incat toate elementele ale caror chei incep cu un bit zero sa fie trecute in fata celor care incep cu 1.
o Aceasta va avea drept consecinta formarea a doua partitii ale tabloului initial,
o Aceste partitii la randul lor se sorteaza independent, conform aceleasi metode dupa cel de-al doilea bit al cheilor elementelor,
o Cele 4 partitii rezultate dupa al 3-lea bit si asa mai departe.
Acest mod de lucru sugereaza abordarea recursiva a implementarii metodei de sortare. Procesul se desfasoara exact ca si la partitionare:
o Se baleaza tabloul de la stanga spre dreapta pana se gaseste un element a carui cheie care incepe cu 1;
o Se baleeaza tabloul de la dreapta spre stanga pana se gaseste un element a carui cheie incepe cu 0;
o Se interschimba cele doua elemente;
o Procesul continua pana cand pointerii de parcurgere se intalnesc formand doua partitii.
o Se reia aceeasi procedura pentru cel de-al doilea bit al cheilor elementelor in cadrul celor doua partitii rezultate s.a.m.d. [2.9.1.a].
PROCEDURE RadixInterschimb (s,d: TipIndice, b:INTEGER);
VAR i,j: TipIndice;
t: TipElement;
BEGIN [2.9.1.a]
IF (d>s) AND (b>=0) THEN
BEGIN
i:= s; j:= d; b:= b-1;
REPEAT
WHILE(biti(a[i].cheie,b,1)=0)AND(i<j) DO i:= i+1;
WHILE(biti(a[j].cheie,b,1)=1)AND(i<j) DO j:= j+1;
t:= a[i]; a[i]:= a[j]; a[j]:= t
UNTIL j=i;
IF biti(a[d].cheie,b,1)= 0 THEN j:= j+1;
RadixInterschimb(s,j-1,b-1);
RadixInterschimb(j,d,b-1);
END
END
Astfel daca se presupune ca tabloul a[1..15] contine chei intregi care au valoarea mai mica decat 25 (adica se reprezinta utilizand 5 cifre binare), atunci apelul RadixInterschimb(1,15,5) va realiza sortarea dupa cum se prezinta schematic in figura 2.9.1.
|
A S O R T I N G E X A M P L E |
A E O L M I N G E A X T P R S |
A E A E G I N M L O S T P R X |
A A E E G I M M L O S R P T |
A A E E G L M N O P R S |
A A E E L M N O R S |
A A E E G I L M N O P R S T X |
||||||||||||||
Fig. 2.9.1. Sortare radix prin interschimbare
O problema serioasa care afecteaza aceasta metoda se refera la degenerarea partitiilor.
o Degenerarea partitiilor apare de obicei in situatia in care cheile sunt reprezentate prin numere mici (care incep cu multe zerouri).
o Aceasta situatie apare frecvent in cazul caracterelor interpretate pe 8 biti.
Din punctul de vedere al performantei, metoda de sortare radix prin interschimbare sorteaza n chei de b biti utilizand un numar de comparatii de biti egal cu n b
o Cu alte cuvinte, sortarea radix prin interschimbare este liniara cu numarul de biti ai unei chei.
o Pentru o distributie normala a bitilor cheilor, metoda lucreaza ceva mai rapid decat metoda quicksort [Se88].
O alta varianta de implementare a sortarii radix este aceea de a examina bitii cheilor elementelor de la dreapta la stanga.
Este metoda utilizata de vechile masini de sortat cartele.
o Teancul de cartele trece de 80 de ori prin masina, cate odata pentru fiecare coloana incepand de la dreapta spre stanga, fiecare trecere realizand sortarea dupa o coloana.
o In cazul cheilor, cand se ajunge la bitul i venind dinspre dreapta, cheile sunt gata sortate pe ultimii i-1 biti ai lor.
o Sortarea continua extragand toate elementele ale caror chei au zero pe pozitia i si plasandu-le in fata celor care au 1 pe aceeasi pozitie.
Nu este usor de demonstrat ca metoda este corecta: de fapt ea este corecta numai in situatia in care sortarea dupa 1 bit este stabila.
Datorita acestei cerinte, sortarea radix prin interschimbare nu poate fi utilizata deoarece nu este o metoda de sortare stabila.
PROCEDURE RadixDirect;
VAR i,j,trecere: integer;
numar: ARRAY[0..m1-1] OF integer;
BEGIN
FOR trecere:= 0 TO (b DIV m)-1 DO
BEGIN [2.9.2.a]
FOR j:= 0 TO m1-1 DO numar[j]:= 0;
FOR i:= 1 TO n DO
numar[biti(a[i].cheie,trecere*m,m)]:=
numar[biti(a[i].cheie,trecere*m,m)] + 1;
FOR j:= 1 TO m1-1 DO
numar[j]:= numar[j-1]+numar[j];
FOR i:= n DOWNTO 1 DO
BEGIN
t[numar[biti(a[i].cheie,trecere*m,m)]]:=
a[i];
numar[biti(a[i].cheie,trecere*m,m)]:=
numar[biti(a[i].cheie,trecere*m,m)]-1
END;
FOR i:= 1 TO n DO a[i]:= t[i]
END
END;
Ca performanta, sortarea radix directa:
o Poate sorta n elemente cu chei de b biti in b/m treceri,
o Utilizand spatiu suplimentar de memorie pentru 2m contoare
o Si un buffer pentru rearanjarea tabloului cu dimensiunea egala cu cea a tabloului original.
Timpul de executie al celor doua metode de sortare radix fundamentale, pentru n elemente avand chei de b biti este in esenta proportional cu n * b .
Pe de alta parte, timpul de executie poate fi aproximat ca fiind n log (n) , deoarece daca toate cheile sunt diferite, b trebuie sa fie cel putin log (n) .
In realitate, nici una din metode nu atinge de fapt limita precizata n * b :
o Metoda de la stanga la dreapta se opreste cand apare o diferenta intre chei,
o Metoda de la dreapta la stanga poate prelucra mai multi biti deodata.
Sortarile radix se bucura de urmatoarele proprietati [Se88].
o Proprietatea 1. Sortarea radix prin interschimbare examineaza in medie n log (n) biti.
o Proprietatea 2. La sortarea a n chei de cate b biti, ambele sortari radix examineaza de regula mai putini decat n * b biti.
o Proprietatea Sortarea radix directa poate sorta n elemente cu chei de b biti, in b/m treceri utilizand un spatiu suplimentar pentru 2m contoare si un buffer pentru rearanjarea tabloului.
Sortarea radix directa, anterior prezentata realizeaza b/m treceri prin tabloul de sortat.
Daca se alege pentru m o valoare suficient de mare se obtine o metoda de sortare foarte eficienta, cu conditia sa existe un spatiu suplimentar de memorie cu 2m locatii.
O alegere rezonabila a valorii lui m este b/4 (un sfert din dimensiunea cheii) sortarea radix reducandu-se in acest caz la 4 sortari bazate pe determinarea distributiilor, care sunt practic liniare.
o De obicei valorile m = 4 sau m = 8 sunt propice pentru actuala organizare a sistemelor de calcul si conduc la dimensiuni rezonabile ale tabloului de contoare (16 respectiv 256 de locatii).
o In consecinta fiecare pas este liniar si deoarece sunt necesari numai 8 (4) pasi pentru chei de 32 de biti, procesul de sortare este practic liniar.
o Rezulta astfel este una din cele mai performante metode de sortare, care concureaza metoda quicksort, departajarea intre ele fiind o problema dificila.
Dezavantajele majore ale metodei sunt:
o Necesitatea distributiei uniforme a cheilor
o Necesitatea unor spatii suplimentare de memorie pentru tabloul de contoare si pentru zona de sortare.
In situatia in care tablourile de sortat au elemente de mari dimensiuni, regia mutarii acestor elemente in procesul sortarii este mare.
De aceea este mult mai convenabil ca algoritmul de sortare sa opereze indirect asupra tabloului original prin intermediul unui tablou de indici, urmand ca tabloul original sa fie sortat ulterior intr-o singura trecere.
o Astfel, unui tablou a[1..n] cu elemente de mari dimensiuni,
o I se asociaza un tablou de indici (indicatori) p[1..n];
o Initial se defineste p[i]:=i pentru i=1,n;
o Algoritmul utilizat in sortare se modifica astfel incat sa se acceseze elementele tabloului a prin constructia a[p[i]] in loc de a[i].
o Accesul la a[i] prin p[i] se va realiza numai pentru comparatii, mutarile efectuandu-se in tabloul p[i].
o Cu alte cuvinte algoritmul va sorta tabloul de indici astfel incat p[1] va contine indicele celui mai mic element al tabloului a, p[2] indicele elementului urmator, etc.
In acest mod se evita regia mutarii unor elemente de mari dimensiuni. Se realizeaza de fapt o sortare indirecta a tabloului a.
Principial o astfel de sortare este prezentata in figura 2.10.
Tabloul a inainte de sortare:
1 2 3 4 5 6 7 8 9 10
|
32 |
22 |
|
|
|
16 |
99 |
4 |
3 |
50 |
Tabloul de indici p inainte de sortare:
1 2 3 4 5 6 7 8 9 10
|
|
2 |
|
|
|
6 |
|
8 |
9 |
10 |
Tabloul a dupa sortare:
1 2 3 4 5 6 7 8 9 10
|
32 |
22 |
|
|
|
16 |
99 |
4 |
3 |
50 |
Tabloul de indici p dupa sortare:
1 2 3 4 5 6 7 8 9 10
|
|
4 |
|
|
|
|
|
1 |
10 |
|
Fig. 2.10. Exemplu de sortare indirecta
Aceasta idee poate fi aplicata practic oricarui algoritm de sortare.
Pentru exemplificare in secventa [2.10.a] se prezinta un algoritm care realizeaza sortarea indirecta bazata pe metoda insertiei a unui tablou a.
VAR a: ARRAY[0..n] OF TipElement;
p: ARRAY[0..n] OF TipIndice;
PROCEDURE InsertieIndirecta;
VAR i,j,v: TipIndice;
BEGIN [2.10.a]
FOR i:= 0 TO n DO p[i]:= i;
FOR i:= 2 TO n DO
BEGIN
v:= p[i]; a[0]:= a[i]; j:= i-1;
WHILE a[p[j]].cheie>a[v].cheie DO
BEGIN
p[j+1]:= p[j];
j:= j-1
END;
p[j+1]:= v
END
END;
Dupa cum se observa, cu exceptia atribuirii fanionului, accesele la tabloul a se realizeaza numai pentru comparatii.
In multe aplicatii este suficienta numai obtinerea tabloului p nemaifiind necesara si permutarea elementelor tabloului. Spre exemplu, in procesul tiparirii, elementele pot fi listate in ordine, referirea la ele realizandu-se simplu, in mod indirect prin tabloul de indici.
Daca este absolut necesara mutarea, cel mai simplu acest lucru se poate realiza intr-un alt tablou b.
Daca acest lucru nu se accepta, se poate utiliza procedura de reasezare in situ din secventa [2.10.b].
PROCEDURE MutareInSitu;
VAR i,j,k: TipIndice;
t: TipElement;
BEGIN
FOR i:= 1 TO n DO
IF p[i]<>i THEN [2.10.b]
BEGIN
t:= a[i]; k:= i;
REPEAT
j:= k; a[j]:= a[p[j]];
k:= p[j]; p[j]:= j;
UNTIL k=i;
a[j]:= t
END
END;
In cazul unor aplicatii particulare, viabilitatea acestei tehnici depinde de lungimea relativa a cheilor si articolelor.
Desigur ea nu se justifica pentru articole mici deoarece necesita o zona de memorie suplimentara pentru tabloul p si timp suplimentar pentru comparatiile indirecte.
Pentru articole de mari dimensiuni se indica de regula sortarea indirecta, fara a se mai realiza permutarea efectiva a elementelor.
Pentru articolele de foarte mari dimensiuni metoda se indica a se utiliza integral, inclusiv permutarea elementelor [Se88].
Metodele de sortare prezentate in paragraful anterior nu pot fi aplicate unor date care nu incap in memoria centrala a sistemului, dar care pot fi spre exemplu memorate pe dispozitive periferice secventiale cum ar fi benzile magnetice.
In acest caz datele pot fi descrise cu ajutorul unei structuri de tip secventa avand drept caracteristica esentiala faptul ca in fiecare moment este accesibila doar o singura componenta.
Aceasta este o restrictie foarte severa comparativ cu accesul direct oferit de structura tablou, motiv pentru care tehnicile de sortare sunt de cu totul alta natura.
Una dintre cele mai importante tehnici de sortare a secventelor este sortarea prin 'interclasare' (merging).
Interclasarea presupune combinarea a doua sau mai multe secvente ordonate intr-o singura secventa ordonata, prin selectii repetate ale componentelor curent accesibile.
Interclasarea este o operatie simpla, utilizata ca auxiliar in procesul mult mai complex al sortarii secventiale.
O metoda de sortare bazata pe interclasare a unei secvente a este urmatoarea:
1. Se imparte secventa de sortat a in doua jumatati b si c.
2. Se interclaseaza b cu c, combinand cate un element din fiecare, in perechi ordonate obtinandu-se o noua secventa a.
Se repeta cu secventa interclasata a, pasii 1 si 2 de aceasta data combinand perechile ordonate in qvadruple ordonate.
4. Se repeta pasii initiali, interclasand qvadruplele in 8-uple, s.a.m.d, de fiecare data dubland lungimea subsecventelor de interclasare pana la sortarea intregii secvente.
Spre exemplu fie secventa:
65 12 22 83 18 04 67
Executia pasului 1 conduce la doua jumatati de secventa;
65 12 22
18 04 67
Interclasarea componentelor unice in perechi ordonate conduce la secventa
Injumatatind din nou si interclasand perechile in qvadruple se obtine:
Cea de-a treia injumatatire si interclasarea celor doua qvadruple intr-un 8-uplu conduc la secventa gata sortata:
Fiecare operatie care trateaza intregul set de date se numeste faza;
Procesul prin repetarea caruia se realizeaza sortarea se numeste trecere.
Procesul de sortare anterior descris consta din trei treceri fiecare cuprinzand o faza de injumatatire si una de interclasare.
Pentru a realiza sortarea sunt necesare trei secvente motiv pentru care sortarea se numeste interclasare cu trei secvente. Este de fapt o interclasare neechilibrata cu 3 secvente.
Interclasarea neechilibrata cu trei secvente reprezinta implementarea procedeului de sortare precizat anterior. Schema de principiu a acestui procedeu apare in figura 1.1.
b c a
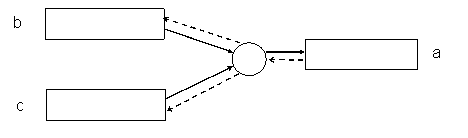
Fig. 1.1. Interclasare neechilibrata cu trei secvente
Intr-o prima etapa in secventele [1.1.a, b] se prezinta structurile de date si schita de principiu a algoritmului.
Dupa cum se observa, fiecare trecere care consta dintr-o reluare a buclei REPEAT, contine doua faze:
O faza de injumatatire adica de distributie a n-uplelor secventei a pe cele doua secvente b si c, respectiv
O faza de interclasare in care n-uplele de pe secventele b si c se interclaseaza in n-uple de dimensiune dubla pe secventa a.
Variabila p initializata pe 1, precizeaza dimensiunea n-uplelor curente, dimensiune care dupa fiecare trecere se dubleaza. In consecinta numarul total de treceri va fi log n
TYPE TipElement = RECORD
cheie: TipCheie;
[1.1.a]
TipSecventa = FILE OF TipElement;
VAR a,b,c: TipSecventa;
PROCEDURE Interclasare3Secvente;
p:= 1; [1.1.b]
REPEAT
*injumatatire;
*interclasare;
Variabila k contorizeaza numarul de n-uple create in procesul de interclasare.
Procesul de sortare se incheie cand in final ramane un singur n-uplu de dimensiune n (k=1).
In continuare se procedeaza la rafinarea celor doua faze.
In secventa [1.1.c] apare primul pas de rafinare al fazei de injumatatire, iar in secventa urmatoare rafinarea enuntului "scrie un n-uplu de dimensiune p in secventa d".
PROCEDURE Injumatatire(p: integer);
RESET(a); REWRITE(b); REWRITE(c);
WHILE NOT Eof(a) DO BEGIN [1.1.c]
*scrie un n-uplu pe b
*scrie un n-uplu pe c
END;
PROCEDURE ScrieNuplu(d: TipSecventa);
i:= 0;
WHILE (i<p) AND NOT Eof(a) DO BEGIN
*citeste(a,x); [1.1.d]
*scrie(d,x)
i:= i+1
END
Variabila i reprezinta contorul de elemente care poate lua valori intre 0 si p. Scrierea se termina la atingerea numarului p de elemente sau la terminarea secventei sursa.
Rafinarea fazei de interclasare apare in secventa [1.1.e].
Variabila de intrare p reprezinta dimensiunea n-uplelor care se interclaseaza, iar k este contorul de n-uple.
Practic interclasarea propriu-zisa (bucla REPEAT) se incheie la terminarea prelucrarii secventelor b si c.
PROCEDURE Interclasare(p: integer; VAR k: integer);
Rewrite(a); Reset(b); Reset(c);
k:= 0; [1.1.e]
initializare interclasare
citeste in x respectiv in y primul element din b
respectiv din c
REPEAT
*interclaseaza cate un n-uplu de pe b si c pe a
UNTIL EndPrelucr_b AND EndPrelucr_c
Close(a); Close(b); Close(c);
Datorita particularitatilor de implementare a fisierelor sunt necesare cateva precizari:
Variabila Eof(f) se pozitioneaza pe true la citirea ultimului element al fisierului f.
Citirea dintr-un fisier cu Eof pozitionat pe true conduce la eroare.
Din punctul de vedere al algoritmului de interclasare, terminarea prelucrarii unui fisier nu coincide cu pozitionarea lui Eof pe true, deoarece mai trebuie prelucrat ultimul element citit.
Pentru rezolvarea acestor constrangeri se utilizeaza tehnica scrutarii (lookahead).
Tehnica scrutarii consta in introducerea unei intarzieri intre momentul citirii si momentul prelucrarii unui element.
Astfel in fiecare moment se prelucreaza elementul citit in pasul anterior si se citeste un nou element.
In acest scop pentru fiecare fisier implicat in prelucrare se utilizeaza o variabila speciala de TipElement pentru memorarea elementului curent, in tandem cu o variabila booleana EndPrelucrare a carei valoare true semnifica terminarea prelucrarii ultimului element al fisierului.
Rafinarea enuntului "interclaseaza cate un n-uplu de pe b si c pe a" apare in secventa [1.1.f ] care aplica tehnica anterior precizata.
Variabilele specifice asociate secventelor b si c sunt x si y respectiv EndPrelucr_b si EndPrelucr_c.
i:= 0;
j:= 0;
WHILE (i<p)AND(j<p) AND NOT EndPrelucr_b AND
NOT EndPrelucr_c DO
BEGIN
IF x.cheie<y.cheie THEN BEGIN
*scrie(a,x); i:= i+1;
*citeste(b,x) [1.1.f]
END
ELSE BEGIN
*scrie(a,y); j:= j+1;
*citeste(c,y)
END
END
*copiaza restul n-uplului de pe b pe a (daca exista)
*copiaza restul n-uplului de pe c pe a (daca exista)
k:= k+1;
O varianta de implementare integrala a procesului de sortare neechilibrata cu 3 benzi apare in PROCEDURA Interclasare3Secvente secventa [1.1.g].
PROCEDURE Interclasare3Secvente;
VAR a,b,c: TipSecventa;
p,k: integer;
PROCEDURE Injumatatire(p: Integer);
VAR x: TipElement;
PROCEDURE ScrieNuplu(VAR d: TipBanda);
VAR i: integer;
BEGIN
i:= 0;
WHILE (i<n) AND (NOT Eof(a)) DO BEGIN
Read(a,x);
Write(d,x); i:= i+1
END
END [1.1.g]
BEGIN
Reset(a); Rewrite(b); Rewrite(c);
WHILE NOT Eof(a) DO BEGIN
ScrieNuplu(b); ScrieNuplu(c);
END
Close(a); Close(b); Close(c);
END
PROCEDURE Interclasare(p: integer; VAR k: integer);
VAR i,j: integer;
x,y: TipElement;
EndPrelucr_b,EndPrelucr_c: Boolean;
BEGIN
Reset(b); Reset(c); Rewrite(a); k:= 0;
EndPrelucr_b:= Eof(b); EndPrelucr_c:= Eof(c);
IF NOT EndPrelucr_b THEN Read(b,x);
IF NOT EndPrelucr_c THEN Read(c,y);
REPEAT
i:= 0; j:= 0;
WHILE (i<p)AND(j<p) AND NOT EndPrelucr_b AND
NOT EndPrelucr_c DO BEGIN
IF x.cheie < y.cheie THEN
BEGIN
Write(a,x); i:= i+1;
IF Eof(b) THEN EndPrelucr_b:= true
ELSE
Read(b,x)
END
ELSE
BEGIN
Write(a,y); j:= j+1;
IF Eof(c) THEN EndPrelucr_c:= true
ELSE
Read(c,y)
END
END
WHILE (i<n) AND NOT EndPrelucr_b DO BEGIN
Write(a,x); i:= i+1;
IF Eof(b) THEN
EndPrelucr_b:= true
ELSE
Read(b,x)
END
WHILE (j<n) AND NOT EndPrelucr_c DO BEGIN
Write(a,y); j:= j+1;
IF Eof(c) THEN
EndPrelucr_c:= true
ELSE
Read(c,y)
END
k:= k+1;
UNTIL EndPrelucr_b AND EndPrelucr_c;
Close(a); Close(b); Close(c);
END;
BEGIN
p:= 1;
REPEAT
Injumatatire(p);
Interclasare(p,k);
p:= p*2;
UNTIL k=1;
END
Faza de injumatatire care de fapt nu contribuie direct la sortare (in sensul ca ea nu permuta nici un element), consuma jumatate din operatiile de copiere.
Acest neajuns poate fi remediat prin combinarea fazei de injumatatire cu cea de interclasare.
Astfel simultan cu interclasarea se realizeaza si redistribuirea n-uplelor interclasate pe doua secvente care vor constitui sursa trecerii urmatoare.
Acest proces se numeste interclasare cu o singura faza sau interclasare echilibrata cu 4 secvente (2 cai).
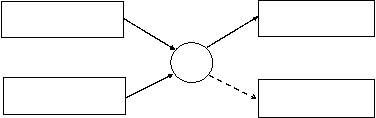
Fig. 1.2.a. Interclasare echilibrata cu patru secvente
Intr-o prima etapa, se va prezenta un program de interclasare al unui tablou, care va fi parcurs strict secvential.
Intr-o etapa ulterioara, interclasarea va fi aplicata unor structuri de tip fisier, permitand compararea celor doua abordari si in acelasi timp demonstrand puternica dependenta a formei programului fata de structurile de date pe care le utilizeaza.
Un tablou poate fi utilizat in locul a doua fisiere, daca este privit ca o secventa cu doua capete.
Astfel in loc de a interclasa doua fisiere sursa, elementele se vor lua de la cele doua capete ale tabloului.
Faza combinata injumatatire-interclasare apare reprezentata schematic in figura 1.2.b.
Destinatia articolelor interclasate este comutata dupa fiecare pereche ordonata la prima trecere, dupa fiecare quadruplu la a doua trecere, s.a.m.d, astfel incat cele doua secvente destinatie, sunt de fapt cele doua capete ale unui singur tablou.
Dupa fiecare trecere cele doua tablouri se interschimba sursa devenind noua destinatie si reciproc.
i j k l Interclasare Injumatatire

SURSA DESTINATIE
Fig. 1.2.b. Model tablou pentru interclasarea echilibrata
In continuare lucrurile se pot simplifica reunind cele doua tablouri conceptuale intr-unul singur de lungime dubla:
a: ARRAY[1..2*n] OF TipElement;
In acest tablou, indicii i si j precizeaza doua elemente sursa, iar k si l doua destinatii.
Secventa initiala va fi continuta de prima parte a tabloului a[1],,a[n].
Se introduce o variabila booleana sus care va preciza sensul miscarii elementelor; de la a[1],,a[n] spre a[n+1],,a[2*n] cand sus este adevarat si in sens invers cand sus este fals. In mod evident valoarea lui sus alterneaza de la o trecere la alta.
Se mai introduce o variabila p care precizeaza lungimea subsecventelor ce urmeaza sa fie interclasate: valoarea sa initiala 1, se dubleaza dupa fiecare trecere.
Pentru a simplifica si mai mult lucrurile se presupune ca n este o putere a lui 2.
In aceste conditii, in secventa [1.2.a] apare varianta pseudocod a procedurii de interclasare iar in secventa [1.2.b] primul pas de rafinare.
PROCEDURE Interclasare
sus: boolean;
p: integer; [1.2.a]
sus:= true; p:= 1;
![]() repeta
repeta
![]() daca
sus atunci
daca
sus atunci
stanga <- sursa; dreapta <- destinatie
altfel
dreapta <- sursa; stanga <- destinatie;
*se interclaseaza secventele de lungime p de la
doua capete ale sursei, alternativ in cele
doua capete ale destinatiei;
sus:= not sus; p:= 2*p
pana cand p=n;
PROCEDURE Interclasare;
VAR i,j,k,l: indice;
sus: boolean; p: integer;
BEGIN
sus:= true; p:= 1;
REPEAT
IF sus THEN
BEGIN
i:= 1; j:= n; k:= n+1; l:= 2*n
END
ELSE [1.2.b]
BEGIN
k:= 1; l:= n; i:= n+1; j:= 2*n
END
*interclaseaza p‑tuplele secv. i‑j in secv. k‑l
sus:= NOT sus; p:= 2*p
UNTIL p=n
END
Interclasarea este de fapt o bucla REPEAT pentru p mergand de la 1 la n.
La fiecare trecere p se dubleaza iar sus comuta.
In cadrul unei treceri:
Functie de variabila sus se asigneaza indicii sursa-destinatie
Se interclaseaza p-tuplele secventelor sursa in p-tuple de dimensiune dubla si se depun in secventa destinatie.
In pasul urmator al detalierilor succesive se rafineaza, enuntul 'interclaseaza p-tuplele secventei i-j in secventa k-l'.
Este clar ca interclasarea a n elemente este la randul ei o succesiune de interclasari partiale ale unor subsecvente de lungime precizata p, in particular p-tuple.
Dupa fiecare astfel de interclasare partiala, destinatia este comutata de la un capat al tabloului destinatie la celalalt, asigurand astfel distributia egala a subsecventelor .
Daca destinatia elementului interclasat este capatul inferior al tabloului destinatie, atunci k este indicele destinatie si valoarea sa este incrementata cu 1 dupa fiecare mutare.
Daca mutarile se executa la capatul superior, atunci l este indicele destinatie si valoarea sa va fi decrementata cu 1 dupa fiecare mutare.
Pentru simplificare, destinatia va fi precizata tot timpul de indicele k, intercomutand valorile lui k si l dupa interclasarea fiecarui p-tuplu si precizand pentru incrementul permanent h valoarea 1 respectiv -1.
Rezulta urmatoarea rafinare [1.2.c]:
h:= 1; m:= n;
REPEAT
q:= p; r:= p; m:= m‑2*p; [1.2.c]
*interclaseaza q elemente de la i cu r elemente de
la j; indicele destinatie este k cu ratia h
h:= ‑h;
*interschimba indicii destinatie (k si l)
UNTIL m=0;
Referitor la secventa [1.2.c] se precizeaza urmatoarele:
S-au notat cu r respectiv q lungimile secventelor care se interclaseaza. De regula la inceputul intercalsarii r=q=p, ele modificandu-se eventul in zona finala daca n nu este putere a lui 2.
S-a notat cu m numarul de elemente care mai sunt de interclasat in cadrul unei treceri. Initial m = n si el scade dupa fiecare interclasare a doua subsecvente cu 2 p .
Procesul de intercalsare pentru o trecere se incheie cand m=0.
Pasul urmator de detaliere rezolva interclasarea. In prealabil se precizeaza faptul ca in situatia in care procesul de interclasare nu epuizeaza o subsecventa, restul ramas neprelucrat trebuie adaugat secventei destinatie printr-o simpla operatie de copiere [1.2.d].
WHILE (q<>0) AND (r<>0) DO
BEGIN
IF a[i].cheie<a[j].cheie THEN
BEGIN
*muta un element de la i la k, avanseaza i si k
q:= q‑1
END
ELSE [1.2.d]
BEGIN
*muta un element de la j la k, avanseaza j si k
r:= r‑1
END
END
copiaza restul secventei i
copiaza restul secventei j
Inainte de a se trece la redactarea propriu-zisa a programului, se va elimina restrictia ca n sa fie o putere a lui 2.
In acest caz, se continua interclasarea p-tuplelor pana cand secventele sursa care raman au lungimea mai mica decat p.
Se observa usor ca singura parte de program care este influentata de aceasta situatie este aceea in care se determina valorile lui q si r, care sunt lungimile secventelor de interclasat din [1.2.c].
In consecinta cele trei instructii:
q:= p; r:= p; m:= m-2*p;
Vor fi inlocuite cu:
IF m>=p THEN q:= p ELSE q:= m; m:= m-q;
IF m>=p THEN r:= p ELSE r:= m; m:= m-r;
unde m este numarul de elemente care au mai ramas de interclasat.
In plus, conditia care controleaza terminarea programului p= n, trebuie modificata in p n.
Varianta finala a procedurii Interclasare apare in [1.2.e]
PROCEDURE Interclasare;
VAR i,j,k,l,t: indice;
h,m,p,q,r: integer; sus: boolean;
BEGIN
sus:= true; p:= 1;
REPEAT
h:= 1; m:= n; [1.2.e]
IF sus THEN
BEGIN
i:= 1; j:= n; k:= n+1; l:= 2*n
END
ELSE
BEGIN
k:= 1; l:= n; i:= n+1; j:= 2*n
END;
REPEAT
IF m>=p THEN q:= p ELSE q:= m; m:= m‑q;
IF m>=p THEN r:= p ELSE r:= m; m:= m‑r;
WHILE(q<>0) AND (r<>0) DO
BEGIN
IF a[i].cheie<a[j].cheie THEN
BEGIN
a[k]:= a[i]; k:= k+h; i:= i+1; q:= q‑1
END
ELSE
BEGIN
a[k]:= a[j]; k:= k+h; j:= j‑1; r:= r‑1
END
END;
WHILE r<>0 DO
BEGIN
a[k]:= a[j]; k:= k+h; j:= j‑1; r:= r‑1
END;
WHILE q<>0 DO
BEGIN
a[k]:= a[j]; k:= k+h; i:= i+1; q:= q‑1
END;
h:= ‑h; t:= k; k:= l; l:= t
UNTIL m=0;
sus:= NOT sus; p:= 2*p
UNTIL p>=n;
IF NOT sus THEN
FOR i:= 1 TO n DO a[i]:= a[i+n]
END
Analiza interclasarii. Deoarece la fiecare trecere p se dubleaza, indeplinirea conditiei p > n presupune log2 n treceri, deci o eficienta de ordinul O( log 2 n).
Fiecare pas, prin definitie, copiaza intregul set de n elemente exact odata, prin urmare numarul de miscari M este cunoscut exact:
M = n log2 n
Numarul de comparatii C este chiar mai mic decat M deoarece operatia de copiere a resturilor nu presupune nici o comparatie.
Cu toate astea, intrucat tehnica interclasarii presupune utilizarea unor dispozitive periferice, efortul de calcul necesar operatiilor de mutare poate domina efortul necesar operatiilor de comparare cu mai multe ordine de marime, motiv pentru care analiza numarului de comparatii nu prezinta interes.
In aparenta tehnica interclasarii obtine performante la nivelul celor mai performante tehnici de sortare.
In realitate insa:
Regia manipularii indicilor este relativ ridicata,
Necesarul dublu de zona de memorie este un dezavantaj decisiv.
Din aceste motive aceasta tehnica este rar utilizata in sortarea tablourilor.
Masuratorile reale efectuate situeaza tehnica interclasarii la nivelul performantelor metodei heapsort, deci sub performantele quicksortului.
Tehnica de sortare prin interclasare nu ia in considerare faptul ca datele initiale pot fi partial sortate, subsecventele avand o lungime predeterminata (2k in trecerea k).
De fapt, oricare doua subsecvente ordonate de lungimi m si n pot fi interclasate intr-o singura subsecventa ordonata de lungime m+n.
Tehnica de interclasare care in fiecare moment combina cele mai lungi secvente ordonate posibile se numeste sortare prin interclasare naturala.
In cadrul acestei tehnici un rol central il joaca notiunea de monotonie, care va fi clarificata pe baza urmatorului exemplu.
Se considera urmatoarea secventa de chei,
13
Se pun linii verticale la extremitatile secventei precum si intre elementele aj si aj+1, ori de cate ori aj > aj+1.
In felul acesta secventa a fost defalcata in secvente partiale monotone.
Acestea sunt de lungime maxima, adica nu pot fi prelungite fara a-si pierde proprietatea de a fi monotone.
In general fie a1,a2, , an o secventa oarecare de numere intregi. Se intelege prin monotonie orice secventa partiala ai,,aj care satisface urmatoarele conditii:
1) 1 i j n ;
2) ak ak+1 pentru orice i k <j;
3) ai-1 > ai sau i = 1 ; [2.a]
4) aj > aj+1 sau j = n .
Aceasta definitie include si monotoniile cu un singur element, deoarece in acest caz i=j si proprietatea 2 este indeplinita, neexistand nici un k cuprins intre i si j-1.
Sortarea naturala interclaseaza monotonii.
Sortarea se bazeaza pe urmatoarea proprietate:
Daca se intercaleaza doua secvente a cate n monotonii fiecare, rezulta o secventa cu exact n monotonii.
Ca atare la fiecare trecere numarul acestora se injumatateste si in cel mai rau caz, numarul necesar de miscari este n* log2 n , in medie mai redus.
Numarul de comparatii este insa mult mai mare deoarece pe langa comparatiile necesare interclasarii elementelor sunt necesare comparatii intre elementele consecutive ale fiecarui fisier pentru a determina sfarsitul fiecarei monotonii.
In continuare in dezvoltarea programului aferent acestei tehnici va fi utilizata metoda detalierilor succesive.
Se va utiliza o structura de date de tip fisier secvential asupra careia se va aplica sortarea prin interclasare neechilibrata in doua faze, utilizand trei secvente.
Algoritmul lucreaza cu secventele a, b si c. Secventa c este cea care trebuie procesata si care in final devine secventa sortata. In practica, din motive de securitate, c este de fapt o copie a secventei initiale.
Se utilizeaza urmatoarele structuri de date [2.b].
TYPE TipSecventa = FILE OF TipElement; [2.b]
VAR a,b,c: TipSecventa;
Secventele a si b sunt auxiliare si ele servesc la defalcarea provizorie a lui c pe monotonii.
Fiecare trecere consta din doua faze alternative care se numesc defalcare respectiv interclasare.
In faza de defalcare monotoniile secventei c se defalca alternativ pe secventele a si b.
In faza de interclasare se recombina in c, monotoniile de pe secventele a si b (fig. 2).
c defalcare trecere 1 trecere 2 trecere n c c c c a a a b b b
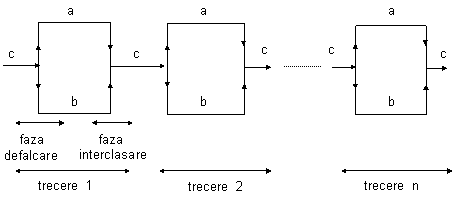
Fig. 2. Treceri si faze in interclasarea naturala
Sortarea se termina in momentul in care numarul monotoniilor secventei c devine egal cu 1.
Pentru numararea monotoniilor se utilizeaza variabila l.
Prima forma a algoritmului apare in secventa [2.c].
Cele doua faze apar ca doua instructii, care in continuare urmeaza sa fie rafinate.
Procesul de rafinare poate fi realizat
Fie prin substitutia directa a celor doua instructii cu secventele care le corespund (tehnica insertiei),
Fie prin interpretarea lor ca proceduri si procedand in consecinta la dezvoltarea lor (tehnica selectiei).
PROCEDURE InterclasareNaturala;
VAR l: integer;
a,b,c: TipSecventa;
sm: boolean;
BEGIN [2.c]
REPEAT
Rewrite(a); Rewrite(b); Reset(c);
Defalcare;
Reset(a); Reset(b); Rewrite(c);
l:= 0;
Interclasare;
UNTIL l=1
END
In continuare se va continua procesul de rafinare prin tehnica selectiei.
In secventele [2.d] respectiv [2.e] apar primii pasi de rafinare pentru Defalcare respectiv Interclasare.
PROCEDURE Defalcare;
BEGIN
REPEAT [2.d]
CopiazaMonotonia(c,a);
IF NOT Eof(c) THEN CopiazaMonotonia(c,b)
UNTIL Eof(c)
END
Aceasta metoda de defalcare distribuie fie un numar egal de monotonii pe secventele a respectiv b, fie cu o monotonie mai mult pe secventa a, dupa cum numarul de monotonii de pe secventa c este par respectiv impar.
PROCEDURE Interclasare;
BEGIN
REPEAT
InterclasareMonotonie; l:= l+1;
UNTIL Eof(b);
IF NOT Eof(a) THEN [2.e]
BEGIN
CopiazaMonotonia(a,c); l:= l+1
END
END
Dupa interclasarea monotoniilor perechi, monotonia nepereche (daca exista) trebuie recopiata pe c.
Procedurile Defalcare si Interclasare sunt redactate in termenii unor proceduri subordonate (InterclasareMonotonie, CopiazaMonotonia) care se refera la o singura monotonie si care vor fi rafinate in continuare in [2.f] respectiv [2.g].
Se introduce variabila booleana sm (sfarsit monotonie) care specifica daca s-a ajuns sau nu la sfarsitul unei monotonii. La epuizarea uneia dintre monotonii restul celeilalte este copiat in secventa destinatie.
PROCEDURE CopiazaMonotonia( x,y: TipSecventa);
BEGIN
REPEAT [2.f]
CopiazaElement(x,y)
UNTIL sm
END;
PROCEDURE InterclasareMonotonie;
BEGIN
REPEAT
IF a.elemCurent.cheie < b.elemCurent.cheie THEN
BEGIN
CopiazaElement(a,c);
IF sm THEN CopiazaMonotonia(b,c)
END [2.g]
ELSE
BEGIN
CopiazaElement(b,c);
IF sm THEN CopiazaMonotonia(a,c)
END
UNTIL sm
END;
Pentru redactarea procedurilor de mai sus se utilizeaza o procedura subordonata CopiazaElement(x,y: TipSecventa), care transfera elementul curent al secventei sursa x in secventa destinatie y, pozitionand variabila sm functie de atingerea sau nu a sfarsitului monotoniei.
In acest scop se utilizeaza tehnica 'lookahead' (scrutare in fata), bazata pe citirea in pasul curent a elementului pentru pasul urmator, primul element fiind introdus in tamponul fisierului inaintea demararii procesului de defalcare respectiv de interclasare.
Pentru acest scop se modifica si structura de date aferenta secventei dupa cum urmeaza [2.h].
TYPE TipSecventa = RECORD [2.h]
secventa: FILE OF TipElement;
elemCurent: TipElement;
termPrelucr: boolean
END;
Procedura CopiazaElement apare in secventa [2.i].
PROCEDURE CopiazaElement(VAR x,y: TipSecventa);
VAR aux: TipElement;
BEGIN
Write(y.secventa,x.elemCurent);
IF Eof(x.secventa) THEN
BEGIN
sm:= true; x.termPrelucr:= true
END [2.i]
ELSE
BEGIN
aux:= x.elemCurent;
Read(x.secventa,x.elemCurent);
sm:= aux.cheie > x.elemCurent.cheie
END;
END;
Dupa cum se observa:
La momentul curent se scrie pe secventa destinatie y elementul x.elemCurent citit in pasul anterior
Se citeste noul x.elemCurent in vederea determinarii sfarsitului de monotonie sm sau a sfarsitului prelucrarii termPrelucr. In acest scop se utilizeaza variabila aux: TipElement.
Desigur unii dintre pasii de rafinare precizati pot suferi anumite modificari, functie de natura secventelor reale care se utilizeaza si de setul de operatii disponibile asupra acestora.
Din pacate, programul dezvoltat cu ajutorul acestei metode nu este corect in toate cazurile.
Spre exemplu, defalcarea secventei c cu 10 monotonii:
are drept consecinta datorita distributiei cheilor formarea a 5 monotonii pe secventa a si a unei singure monotonii pe secventa b, in loc de 5 cum era de asteptat.
a:
b:
Faza de interclasare conduce la o secventa cu doua monotonii (in loc de 5)
c:
deoarece in procesul de interclasare s-a ajuns la sfarsitul secventei b si conform lui [2.d] se mai copiaza o singura monotonie din a. Dupa trecerea urmatoare sortarea se incheie, dar rezultatul este incorect:
c:
Acest lucru se intampla deoarece nu a fost luat in considerare faptul ca desi procesul de distribuire repartizeaza in mod egal monotoniile pe secventele a respectiv b, numarul de monotonii pe cele doua secvente poate diferi foarte mult datorita distributiei cheilor.
Pentru a remedia aceasta situatie, este necesar ca procedura Interclasare sa fie modificata astfel incat, in momentul in care se ajunge la sfarsitul unei secvente, sa copieze in c tot restul celeilalte secvente.
Versiunea revizuita a algoritmului de sortare prin interclasare naturala apare in [2.j].
PROCEDURE InterclasareNaturala;
VAR l: integer;
sm: boolean;
a,b,c: TipSecventa;
PROCEDURE CopiazaElement(VAR x,y: TipSecventa);
VAR aux: TipElement;
BEGIN
Write(y.secventa,x.elemCurent);
IF Eof(x.secventa) THEN
BEGIN
sm:= true;
x.termPrelucr:= true
END [2.j]
ELSE
BEGIN
aux:= x.elemCurent;
Read(x.secventa,x.elemCurent);
sm:= aux.cheie > x.elemCurent.cheie
END;
END;
PROCEDURE CopiazaMonotonia(VAR x,y: TipSecventa);
BEGIN
REPEAT
CopiazaElement(x,y)
UNTIL sm
END;
PROCEDURE Defalcare;
BEGIN
Rewrite(a.secventa);Rewrite(b.secventa);
Reset(c.secventa);
c.termPrelucr:= Eof(c.secventa);
Read(c.secventa,c.elemCurent);
REPEAT
CopiazaMonotonia(c,a);
IF NOT c.termPrelucr THEN
CopiazaMonotonia(c,b)
UNTIL c.termPrelucr;
Close(a.secventa); Close(b.secventa);
Close(c.secventa)
END;
PROCEDURE InterclasareMonotonie;
BEGIN
REPEAT
IF a.elemCurent.cheie < b.elemCurent.cheie THEN
BEGIN
CopiazaElement(a,c);
IF sm THEN CopiazaMonotonia(b,c)
END
ELSE
BEGIN
CopiazaElement(b,c);
IF sm THEN CopiazaMonotonia(a,c)
END
UNTIL sm [2.j] continuare
END;
PROCEDURE Interclasare;
BEGIN
Reset(a.secventa); Reset(b.secventa);
Rewrite(c.secventa);
a.termPrelucr:= Eof(a.secventa);
b.termPrelucr:= Eof(b.secventa);
IF NOT a.termPrelucr THEN
Read(a.secventa,a.elemCurent);
IF NOT b.termPrelucr THEN
Read(b.secventa,b.elemCurent);
WHILE NOT b.termPrelucr DO
BEGIN
InterclasareMonotonie; l:= l+1
END;
IF NOT a.termPrelucr THEN
BEGIN
CopiazaMonotonia(a,c); l:= l+1
END;
Close(a.secventa);Close(b.secventa);
Close(c.secventa);
END; {Interclasare
BEGIN
REPEAT
Defalcare;
l:= 0;
Interclasare;
UNTIL l=1;
END
Analiza sortarii prin interclasare naturala.
Dupa cum s-a mai precizat, la analiza unei metode de sortare externa, numarul comparatiilor de chei nu are importanta practica, deoarece durata prelucrarilor in unitatea centrala a sistemului de calcul este neglijabila fata de durata acceselor la memoriile externe.
Din acest motiv numarul mutarilor M va fi considerat drept unic indicator de performanta.
In cazul sortarii prin intercalsare naturala:
La o trecere, in fiecare din cele doua faze (defalcare si interclasare) se muta toate elementele, deci M = 2*n .
Dupa fiecare trecere numarul monotoniilor se micsoreaza de doua ori, uneori chiar mai substantial, motiv pentru care a fost necesara si modificarea anterioara a procedurii Interclasare.
Stiind ca numarul maxim de monotonii initiale este n, numarul maxim de treceri este log2 n , astfel incat in cel mai defavorabil caz numarul de miscari M=2*n* log2 n , in medie simtitor mai redus.
Intrucat efortul de sortare este proportional cu numarul de treceri, o cale de reducere a acestuia este aceea de a distribui monotoniile pe mai mult decat doua secvente.
In consecinta:
Interclasarea a r monotonii care sunt distribuite pe N secvente conduce la o succesiune de r/N monotonii.
Al doilea pas conduce la r/N 2, monotonii
Al treilea la r/N 3, monotonii s.a.m.d.
Aceasta metoda de sortare se numeste interclasare multipla-N.
Numarul total de treceri k, in cazul sortarii a n elemente prin interclasare multipla-N este k = log N n , iar numarul total de miscari M = n log N n
O modalitate de implementare a acestei situatii o reprezinta interclasarea multipla echilibrata care se realizeaza intr-o singura faza.
Interclasarea multipla echilibrata presupune ca la fiecare trecere exista un numar egal de secvente de intrare si de iesire, monotoniile de pe primele fiind interclasate si imediat redistribuite pe celelalte.
Daca se utilizeaza N secvente (N par), avem de fapt de-a face cu o interclasare multipla echilibrata cu N/2 cai.
Schema de principiu a acestei metode apare in figura a.
N/2 secvente sursa N/2 secvente destinatie

Fig. a. Modelul interclasarii multiple echilibrate
Algoritmul care va fi dezvoltat in continuare se bazeaza pe o structura specifica de date: tabloul de secvente.
Fata de procedeul utilizat in paragraful anterior, care era de fapt o interclasare multipla cu 2 cai, trecerea la mai multe cai presupune modificari esentiale:
Procesul de interclasare trebuie sa gestioneze o lista a secventelor active, din care va elimina pe rand secventele ale caror monotonii s-au epuizat.
De asemenea trebuie implementata comutarea grupelor de secvente de intrare si iesire dupa fiecare trecere.
Pentru aceasta se definesc structurile de date din secventa [a].
TYPE TipSecventa = RECORD
fisier: File of TipElement;
curent: TipElement;
termPrelucr: boolean [a]
END;
NrSecventa: 1..n;
VAR f0: TipSecventa;
F: ARRAY[NrSecventa] OF TipSecventa;
t,td: ARRAY[NrSecventa] OF NrSecventa;
Tipul NrSecventa este utilizat ca tip indice al tabloului de secvente F, tablou ale carui elemente apartin lui TipSecventa.
Se presupune ca secventa de elemente care urmeaza sa fie sortata este furnizata ca o variabila f0: TipSecventa si ca pentru procesul de sortare se utilizeaza N secvente (N par).
Problema comutarii secventelor este rezolvata introducand tabloul t care are drept componente indici care identifica secventele.
Astfel in loc de a adresa o secventa din tabloul F direct prin indicele i, aceasta va fi adresata via tabloul t, respectiv F[t[i]] in loc de F[i].
Initial t[i]=i pentru toate valorile lui i,
Comutarea consta de fapt in interschimbarea perechilor de componente ale tabloului dupa cum urmeaza, unde NH = N/2.
t[1] <-> t[NH+1]
t[2] <-> t[NH+2]
.
t[NH] <-> t[N]
In continuare secventele F[t[1]],,F[t[NH]]vor fi considerate intotdeauna secvente de intrare, iar secventele F[t[NH+1]],, F[t[N]]drept secvente de iesire (fig.b).
Tabela de fisiere F
1 2 3 4 5 6
|
B1 |
B2 |
B3 |
B4 |
B5 |
B6 |
Tabloul de indici t (inainte de comutare)
|
|
|
|
|
|
|
NH NH+1
Tabloul de indici t (dupa comutare)
1 2 3 4 5 6
|
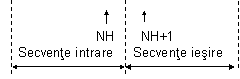 4 4
|
|
|
|
|
|
Fig. b. Comutarea secventelor in interclasarea multipla echilibrata
Forma initiala a algoritmului de sortare este cea din secventa [b].
PROCEDURE SortareMultiplaEchilibrata;
VAR i,j: NrSecventa;
l: integer
t,td: ARRAY[NrSecventa] OF NrSecventa;
F: ARRAY[NrSecventa] OF TipSecventa;
BEGIN [b]
j:= NH; l:= 0;
REPEAT
IF j<NH THEN j:= j+1 ELSE j:= 1;
*copiaza o monotonie de pe f0 pe secventa j
l:= l+1
UNTIL SfarsitPrelucr(f0);
FOR i:= 1 TO n DO t[i]:= i;
REPEAT
*initializare secvente de intrare
l:= 0;
j:= NH+1;
REPEAT
l:= l+1;
*interclaseaza cate o monotonie de pe fiecare
intrare pe t[j]
IF j<N THEN j:= j+1 ELSE j:= NH+1
UNTIL *toate intrarile au fost epuizate
*comuta secventele
UNTIL l=1
END;
Dupa cum se observa, procesul de sortare multipla echilibrata consta din trei pasi.
(1) Primul pas se refera la distributia monotoniilor initiale si este materializat de prima bucla REPEAT. In acest pas:
Monotoniile de pe secventa initiala f0 sunt distribuite succesiv pe secventele sursa care sunt indicate de j.
Dupa copierea fiecarei monotonii, indicele j care parcurge ciclic domeniul [1..NH] este incrementat.
Distributia se termina cand se epuizeaza f0, iar numarul de monotonii distribuite se contorizeaza in l.
(2) Pasul al doilea realizeaza initializarea tabloului t (bucla FOR),
(3) Pasul al treilea realizeaza interclasarea secventelor de intrare F[t[1]]F[t[NH]] in secventele de iesire F[t[NH+1]]F[t[N]].
Principiul interclasarii este urmatorul:
Se iau toate intrarile active si se interclaseaza cate o monotonie de pe fiecare intr-o singura monotonie care se depune pe secventa j.
Se avanseaza la secventa de iesire urmatoare (j parcurge ciclic domeniul [NH+1..N])
Se reia procedeul pana la epuizarea tuturor intrarilor (bucla REPEAT interioara).
In acest moment se comuta secventele (intrarile devin iesiri si invers) si se reia interclasarea.
Procesul continua pana cand numarul de monotonii de interclasat ajunge egal cu 1 (bucla REPEAT exterioara).
In continuare se prezinta rafinarea enunturilor implicate in algoritm.
In secventa [c] apare rafinarea enuntului *copiaza o monotonie de pe f0 in secventa j, utilizat in distributia initiala a monotoniilor.
VAR buf: TipElement;
REPEAT [c]
buf:= f0.curent;
IF Eof(f0.fisier) THEN
f0.termPrelucr:= true
ELSE
Read(f0.fisier, f0.curent);
Write(F[j].fisier,buf)
UNTIL (buf.cheie>f0.curent.cheie) OR f0.termPrelucr;
Urmeaza rafinarea enuntului *initializare secvente de intrare.
Pentru inceput trebuiesc identificate secventele curente de intrare deoarece numarul celor active poate fi mai mic decat N.
De fapt, numarul secventelor se reduce pe masura ce se reduce numarul monotoniilor.
Practic nu pot exista mai multe secvente decat monotonii astfel incat sortarea se termina cand mai ramane o singura secventa.
Se introduce variabila k1 pentru a preciza numarul actual de secvente de intrare active.
Cu aceste precizari secventa de initializare va fi [d]:
[d]
FOR i:= 1 TO k1 DO Reset(F[t[i]]);
Datorita procesului repetat de interclasare, tendinta lui k1 este de a descreste odata cu epuizarea monotoniilor, deci conditia *toate intrarile epuizate se poate exprima prin relatia k1 = 0 .
Enuntul *interclaseaza cate o monotonie de pe fiecare intrare pe t[j] este mai complicat.
El consta in selectia repetata a elementului cu cea mai mica cheie dintre sursele disponibile si trecerea lui pe secventa de iesire curenta.
De la fiecare secventa sursa se parcurge cate o monotonie al carei sfarsit poate fi atins fie:
(1) Prin epuizarea secventei curente;
(2) Prin citirea unei chei mai mici decat cea curenta.
In cazul (1) secventa este eliminata si k1 decrementat.
In cazul (2) secventa este exclusa temporar de la selectia cheilor, pana cand se termina crearea monotoniei curente pe secventa de iesire, operatie numita "inchidere monotonie".
In acest scop se utilizeaza un al doilea indice k2 care precizeaza numarul de secvente sursa disponibile curent pentru selectia cheii urmatoare.
Valoarea sa initiala egala cu k1, se decrementeaza ori de cate ori se epuizeaza o monotonie din cauza conditiei (2).
Cand k2 devine 0, s-a terminat interclasarea cate unei monotonii de la fiecare intrare activa pe secventa de iesire curenta.
Primul pas de rafinare al acestui enunt apare in [d].
FOR i:= 1 TO k1 DO Reset(F[t[i]].fisier);
k2:= k1;
REPEAT
*selecteaza cheia minima. Fie t[mx] indicele
secventei care o contine
buf:= F[t[mx]].curent;
IF Eof(F[td[mx]].fisier) THEN [d]
F[td[mx]].termPrelucr:= true
ELSE
Read(F[td[mx].fisier,F[td[mx].curent);
Write(F[T[j]].fisier,buf);
IF Eof(F[td[mx]].fisier) THEN
*elimina secventa
ELSE
IF buf.cheie>F[t[mx]].curent.cheie THEN
*inchide monotonia
UNTIL k2=0;
Din pacate, introducerea lui k2 nu este suficienta, deoarece pe langa numarul secventelor disponibile trebuie sa se stie exact care sunt acestea.
O solutie in acest sens poate sa o constituie utilizarea unui tablou cu componente booleene care indica disponibilitatea secventelor.
O solutie mai eficienta insa este utilizarea unui al doilea tablou de indici td.
Acest tablou este utilizat in locul lui t pentru secventele de intrare astfel incat td[1],,td[k2] sunt indicii secventelor disponibile.
Tabloul td se initializeaza la inceputul fiecarei interclasari prin copierea indicilor secventelor de intrare din tabloul t ( t[1],,t[k1]).
Indicele k1 se initializeaza pe valoarea N/2 daca numarul de monotonii l este mai mare ca N/2 respectiv cu valoarea lui l in caz contrar (l reprezinta numarul de monotonii interclasate in faza anterioara).
Tabloul td apare reprezentat schematic in figura c.
|
secvente de intrare |
|
k1 |
|
k2 |
|
mx |
|
Tabloul td |
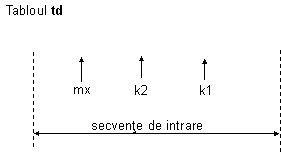 |
1 2 3 N/2
![]()
Fig. c. Tabloul td utilizat ca auxiliar in procesul de interclasare
Indicele k1 precizeaza numarul de secvente active.
Restul secventelor, (pana la N/2) nu mai au monotonii fiind terminate fizic, motiv pentru care acestea nici nu se mai consemneaza.
Indicele k2 care se initializeaza cu valoarea lui k1, precizeaza numarul de secvente care mai au monotonii in trecerea curenta.
Restul secventelor (pana la k1) si-au epuizat monotoniile in trecerea curenta fara a fi insa epuizate fizic.
In aceste conditii, enuntul *inchide monotonia corespunzator conditiei (2), se rafineaza dupa cum urmeaza.
Fie mx indicele secventei pentru care s-a terminat monotonia curenta: se interschimba in td pozitia mx cu pozitia k2 si se decrementeaza k2.
In ceea ce priveste enuntul *elimina secventa, corespunzator conditiei (1), considerand ca tot mx este indicele secventei care s-a epuizat, rafinarea presupune urmatoarele.
Se muta secventa precizata de k2 in locul secventei precizate de mx si secventa precizata de k1 in locul secventei indicate de k2.
Se decrementeaza atat k1 cat si k2.
Forma finala a sortarii multiple echilibrate apare in secventa [e].
PROCEDURE InterclasareMultiplaEchilibrata;
VAR i,j,mx,tx: NrSecventa;
k1,k2,l: integer;
x,min: integer;
t,td: ARRAY[NrSecventa] OF NrSecventa;
F: ARRAY[NrSecventa] OF TipSecventa;
f0: TipSecventa;
BEGIN
FOR i:= 1 TO NH DO Rewrite(f[i])
j:= NH; l:= 0;
Read(f0.fisier,f0.curent);
REPEAT
IF j<NH THEN j:= j+1 ELSE j:= l;
l:= l+1;
REPEAT
buf:= f0.curent; [e]
IF Eof(f0.fisier) THEN
f0.termPrelucr:= true
ELSE
Read(f0.fisier, f0.curent);
Write(F[j].fisier,buf0)
UNTIL (buf.cheie>f0.curent.cheie) OR
f0.termPrelucr;
UNTIL f0.termPrelucr;
FOR i:= 1 TO N DO t[i]:= i;
REPEAT
IF l<NH THEN k1:= l ELSE k1:= NH;
FOR i:= 1 TO k1 DO
BEGIN
Reset(F[t[i]]); td[i]:= t[i];
Read(F[td[i]].fisier,F[td[i]].curent)
END ;
l:= 0;
j:= NH+1;
REPEAT
k2:= k1; l:= l+1;
REPEAT
i:= 1; mx:= 1; min:= F[td[1]].curent.cheie;
WHILE i<k2 DO
BEGIN
i:= i+1; x:= F[td[i]].curent.cheie;
IF x<min THEN
BEGIN min:= x; mx:= i END
END;
buf:= F[td[mx]].curent;
IF Eof(F[td[mx]].fisier) THEN
F[td[mx]].termPrelucr:= true
ELSE
Read(F[td[mx]].fisier,F[td[mx]].curent);
Write(F[td[j]].fisier,buf)
IF F[td[mx]].termPrelucr THEN
BEGIN
Rewrite(F[td[mx]]);
td[mx]:= td[k2]; td[k2]:= td[k1];
k1:= k1‑1; k2:= k2‑1
END
ELSE
IF buf.cheie>F[td[mx]].curent.cheie THEN
BEGIN
tx:= td[mx]; td[mx]:= td[k2];
td[k2]:= tx; k2:= k2‑1
END
UNTIL k2=0;
UNTIL k1=0;
FOR i:= 1 TO NH DO
BEGIN
tx:= t[i]; t[i]:= t[i+NH]; t[i+NH]:= tx
END
UNTIL l=1;
END;
Metoda interclasarii echilibrate contopeste operatiile de distribuire si interclasare intr-o aceeasi faza, utilizand mai multe secvente de intrare si mai multe secvente de iesire, care nu sunt folosite in totalitate.
R.L. Gilstad, a propus metoda sortarii polifazice care inlatura acest neajuns. In plus in cadrul acestei metode insasi notiunea de trecere devine difuza.
Pentru inceput se considera un exemplu cu trei secvente.
In fiecare moment, elementele de pe doua secvente sunt interclasate pe cea de-a treia.
Ori de cate ori una din secventele sursa se epuizeaza, ea devine imediat destinatia operatiei de interclasare a celorlalte doua secvente (secventa neterminata si fosta destinatie).
Dupa cum se cunoaste, din procesul de interclasare a n monotonii de pe fiecare secventa de intrare rezulta n monotonii pe secventa de iesire.
In cadrul acestei metode, pentru simplificare, se va vizualiza numai numarul de monotonii de pe fiecare secventa in locul cheilor propriu-zise.
Astfel, in fig. 4.a (a) se presupune ca secventele de intrare f1 si f2 contin 13 si respectiv 8 monotonii.
La prima 'trecere', sunt interclasate de pe f1 si f2 pe f3 8 monotonii, la a doua 'trecere' sunt interclasate de pe f1 si f3 pe f2 cele 5 monotonii ramase, etc. In final f1 este secventa sortata. In aceeasi figura (b) se prezinta un exemplu de sortare polifazica a 65 de monotonii pe 6 secvente.
|
f1 f2 f3 f1 f2 f3 f4 f5 f6 1 0 2 1 0 1 1 1 1
|
 |
![]()
![]()
![]()
![]()
![]()
![]()
(a) (b)
(a)
(b)
Fig. 4.a. Exemple de sortare polifazica
Aceasta tehnica este mai eficienta decat interclasarea echilibrata deoarece, fiind date N secvente, ea lucreaza la interclasare cu N-1 secvente in loc de N/2.
Astfel numarul de treceri este aproximativ logN n , unde n este numarul de elemente de sortat iar N gradul operatiei de interclasare (numarul de secvente sursa).
In exemplele prezentate insa, distributia initiala a monotoniilor a fost aleasa cu mare grija.
Pentru a determina care dintre distributiile initiale ale monotoniilor asigura o functionare corespunzatoare a algoritmului, se alcatuiesc tabelele din figurile 4.b si 4.c.
Completarea celor doua tabele se realizeaza pornind de la cele doua exemple din fig. 4.a:
Fiecarei treceri ii corespunzande un rand in tablou.
Trecerile se parcurg in ordine inversa (adica de jos in sus).
Fiecare rand din tabel, cu exceptia ultimului, contine pe prima pozitie (a1), numarul de monotonii ale secventei destinatie din trecerea corespunzatoare.
In continuare se trec succesiv in tabel numerele de monotonii corespunzatoare din cadrul trecerii.
Fiecare trecere se parcurge de la stanga la dreapta (incepand cu secventa destinatie) si se considera circulara.
Ultimul rand din tabel contine situatia initiala a distributiei monotoniilor (cea dinaintea demararii procesului de sortare).
|
k |
|
|
|
Fig. 4.b. Distributia perfecta a monotoniilor pe trei secvente
Din tabloul din figura 4.b se pot deduce urmatoarele relatii [4.a]:
![]()
![]()
unde
![]()
![]()
Daca facem
![]()
![]()
![]()
![]()
![]()
Aceasta este insa regula recursiva care defineste numerele lui Fibonacci de ordinul 1:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55,
Fiecare numar din acest sir este suma celor doi predecesori ai sai.
In consecinta, pentru cazul sortarii cu trei secvente, numarul initial al monotoniile pe cele doua secvente trebuie sa fie doua numere Fibonacci consecutive pentru ca sortarea polifazica cu 3 secvente sa functioneze corect.
|
k |
|
|
|
|
|
|
Fig. 4.c. Distributia perfecta a monotoniilor pe 6 secvente
Pentru cel de-al doilea exemplu se obtin urmatoarele formule [4.c]:
![]()
![]()
![]()
![]()
![]()
Daca facem
![]()
![]()
![]()
unde
![]()
![]()
In general, numerele Fibonacci de ordinul p sunt definite dupa cum urmeaza [4.e]:
![]()
![]()
unde
![]()
![]()
![]()
Numerele Fibonacci de ordinul 1 sunt cele obisnuite.
In cazul sortarii polifazice cu n secvente, numerele initiale de monotonii de pe cele n -1 secvente sursa sunt:
O suma de n -1 numere Fibonacci consecutive de ordinul n -2 pe prima secventa,
O suma de n -2 numere Fibonacci consecutive de ordinul n -2 pe a doua secventa,
S.a.m.d.
Pe ultima secventa (cea numerotata cu n -1) trebuie sa existe initial un numar de monotonii egal cu un numar Fibonacci de ordinul n -2.
Aceasta implica faptul ca metoda sortarii polifazice este aplicabila numai in cazul sortarii unei secventei al carei numar initial de monotonii este suma a n -1 de astfel de sume Fibonacci.
O astfel de distributie a monotoniilor initiale se numeste distributie perfecta.
In cazul sortarii polifazice cu 6 secvente (n = 6), sunt necesare numere Fibonacci de ordinul n -2 = 4:
0, 0, 0, 0, 1, 1, 2, 4, 8, 16, 31, 61, 120,
Distributia initiala a monotoniilor, prezentata in fig. 4.a, se stabileste dupa cum urmeaza, pornind de la numarul Fibonacci 8 (cel de-al 9-lea din sir):
Secventa f1 va contine un numar de monotonii egal cu suma a n -1 = 5 numere Fibonacci consecutive: 1 + 1 + 2 + 4 + 8 = 16;
Secventa f2 va contine un numar de monotonii egal cu suma a n -2 = 4 numere Fibonacci consecutive: 1 + 2 + 4 + 8 = 15;
Secventa f3 , o suma de n -3 = 3 numere: 2 + 4 + 8 = 14;
Secventa f4 , o suma de n -4 = 2 numere: 4 + 8 = 12;
Secventa f5 , o suma de n -5 = 1 numere Fibonacci de ordinul 4, adica 8 monotonii.
In total secventa initiala care urmeaza sa fie sortata trebuie sa contina :
16 + 15 + 14 + 12 + 8 = 65 monotonii
Aceste monotonii se distribuie initial pe cele 5 secvente sursa in concordanta cu numerele determinate anterior realizandu-se astfel o distributie perfecta.
Se observa simplu ca in fig. 4.c, distributia monotoniilor pentru fiecare nivel k se obtine aplicand acelasi algoritm, alegand ca baza, numere consecutive din sirul Fibonacci 1, 1, 2, 4, 8, pentru respectiv k = 1, 2, 3, 4, 5, .
Daca numarul initial de monotonii nu satisface conditia de a fi o astfel de suma de n -1 sume Fibonacci, se simuleaza un numar de monotonii ipotetice vide, astfel incat suma sa devina perfecta.
Aceste monotonii se numesc 'fictive'.
Problema care se pune se refera la maniera in care aceste monotonii sunt recunoscute.
Pentru inceput se va investiga problema distributiei initiale a monotoniilor, iar apoi cea a distributiei monotoniilor fictive.
Este evident faptul ca selectia unei monotonii fictive de pe secventa i inseamna ca secventa respectiva este ignorata in timpul interclasarii curente, rezultand o interclasare de pe mai putin de n -1 secvente sursa.
Interclasarea unei monotonii fictive de pe toate cele n -1 secvente sursa nu conduce la nici o interclasare efectiva ci doar la inregistrarea unei monotonii fictive pe secventa de iesire.
Din acest motiv, este necesar ca monotoniile fictive sa fie distribuite cat mai uniform posibil pe cele n -1 secvente.
In primul rand se va analiza problema repartizarii unui numar necunoscut de monotonii pe n -1 secvente. Este clar ca numerele Fibonacci de ordinul n -2 care reprezinta numarul dorit de monotonii pot fi generate in mod progresiv.
Astfel, in cazul n = 6, avand ca reper tabelul din fig. 4.c:
Se porneste cu distributia corespunzatoare lui k = 1 (1,1,1,1,1);
Daca exista mai multe monotonii se trece la randul urmator (2,2,2,2,1),
Apoi la (4,4,4,3,2) s.a.m.d.
Indexul k al randului se numeste nivel. Pe masura ce creste numarul monotoniilor, creste si nivelul numerelor Fibonacci, nivel care in acelasi timp precizeaza si numarul de treceri sau comutari de secvente necesar pentru sortarea respectiva.
Algoritmul de distribuitie poate fi formulat astfel:
1) Fie scopul distributiei, numerele lui Fibonacci de ordin n -2 nivelul l.
2) Se realizeaza distributia monotoniilor conform acestui scop.
3) Daca scopul a fost atins, se calculeaza nivelul urmator de numere Fibonacci; diferenta dintre acestea si numerele corespunzatoare ale nivelului anterior constituie noul scop al distributiei.
4) Se revine la pasul 2.
5) Algoritmul se termina la epuizarea monotoniilor.
Regulile dupa care se calculeaza urmatorul nivel al numerelor lui Fibonacci se bazeaza pe definitia acestora [4.e],
Atentia noastra se va concentra asupra pasului 2, in care in conformitate cu scopul curent se vor distribui monotoniile corespunzatoare una dupa alta pe cele n -1 secvente. In acest pas apar din nou monotoniile fictive.
Se presupune ca la trecerea la nivelul urmator, scopul urmator va fi inregistrat prin diferentele di pentru i = 1,2,,n-1, unde di precizeaza numarul de monotonii care trebuie depus pe secventa i in acest pas.
Se presupune in continuare ca se pun initial di monotonii fictive pe secventa i iar distribuirea monotoniilor poate fi privita ca si o reinlocuire a monotoniilor fictive cu monotonii actuale, de fiecare data inregistrand o inlocuire prin scaderea lui 1 din di.
Cand sursa se epuizeaza, valoarea curenta a lui di indica chiar numarul de monotonii fictive de pe secventa i.
Nu se cunoaste algoritmul care conduce la distributia optima, dar cel propus de Knuth, numit distributie orizontala este foarte bun [Kn76].
Acest termen poate fi inteles considerand monotoniile cladite in forma unor silozuri. In figura 4.d apar reprezentate aceste silozuri de monotonii pentru n = 6 , nivelul 5, conform fig. 4.c.
|
inceput | |||||||||
|
secvente |
f |
f |
f |
f |
f |
||||
Fig.4.d. Distributia orizontala a monotoniilor
Pentru a ajunge cat mai rapid la o distributie egala a monotoniilor fictive, se procedeaza la inlocuirea lor cu monotonii actuale.
Acest proces reduce dimensiunea silozurilor prin extragerea monotoniilor fictive din nivelurile orizontale si inlocuirea lor cu monotonii reale, de la stanga la dreapta.
In acest fel monotoniile sunt distribuite pe secvente dupa cum indica numarul lor de ordine fig. 4.d.
Se precizeaza ca in aceasta figura este reprezentata ordinea de distributie a monotoniilor cand se trece de la nivelul 4 (33 de monotonii) la nivelul 5 (65 de monotonii).
Suprafetele hasurate reprezinta primele 33 de monotonii care au fost deja distribuite cand s-a ajuns la nivelul 4.
Daca spre exemplu ar fi numai 53 de monotonii initiale, toate monotoniile numerotate cu 54 si mai mult vor fi tratate ca fictive.
Monotoniile se inscriu in realitate la sfarsitul secventei, dar este mai avantajos sa ne imaginam ca se scriu la inceput, deoarece in procesul sortarii se presupune ca monotoniile fictive sunt la inceputul secventei.
Pentru inceput se abordeaza descrierea procedurii SelecteazaSecventa care este apelata de fiecare data cand trebuie copiata o noua monotonie.
Procedura realizeaza selectia noii secvente pe care se va copia urmatoarea monotonie tinand cont de distributia perfecta a monotoniilor pe secventele sursa.
Se presupune ca variabila j este indexul secventei curente de destinatie. Se utilizeaza tipurile de date definite in [4.g]:
TYPE TipSecventa = RECORD
fisier: FILE OF TipElement;
curent: TipElement;
termPrelucr: boolean [4.g]
END;
NrSecventa: 1..n;
VAR j: NrSecventa;
a,d: ARRAY[NrSecventa] OF integer;
nivel: integer;
Tablourile a si d memoreaza numerele de distributii reale respectiv fictive corespunzatoare fiecarei secvente i .
Aceste tablouri se initializeaza cu valorile ai = 1, di = 1 pentru i = 1,,n -1 respectiv an = 0, dn = 0 .
Variabilele j si nivel se initializeaza cu valoarea 1.
Procedura SelecteazaSecventa va calcula de fiecare data cand creste nivelul, valorile randului urmator al tabelei din figura 4.c, respectiv valorile a1(k),,an- (k).
Tot atunci se calculeaza si diferentele di = ai(k) - ai(k-1), care reprezinta scopul urmator.
Algoritmul se bazeaza pe faptul ca valorile di descresc odata cu cresterea indicilor (vezi fig. 4.d).
Se precizeaza ca algoritmul incepe cu nivelul 1 (nu cu nivelul 0).
Procedura se termina cu decrementarea cu o unitate a lui dj ceea ce corespunde inlocuirii unei monotonii fictive cu una reala pe secventa j [4.h].
PROCEDURE SelecteazaSecventa;
VAR i: NrSecventa; z: integer;
BEGIN
IF d[j]<d[j+1] THEN j:= j+1
ELSE
BEGIN
IF d[j]=0 THEN [4.h]
BEGIN
nivel:= nivel+1; z:= a[1];
FOR i:= 1 TO n-1 DO
BEGIN
d[i]:= z+a[i+1]-a[i]
a[i]:= z+a[i+1]
END
END;
j:= 1
END;
d[j]:= d[j]-1
END; [SelecteazaSecventa]
Presupunand ca se dispune de o rutina de copiere a unei monotonii de pe secventa sursa f0 pe secventa F[j], faza initiala de distribuire a monotoniilor poate fi schitata astfel [4.i]:
REPEAT
SelecteazaSecventa; [4.i]
CopiazaMonotonia
UNTIL f0.termPrelucr;
Spre deosebire de interclasarea naturala, in cea polifazica este necesar sa se cunoasca numarul exact de monotonii de pe fiecare secventa, deoarece procesul de interclasare poate conduce la diminuarea numarului de monotonii.
Pentru aceasta se va retine cheia ultimului element al ultimei monotonii de pe fiecare secventa. In acest scop se introduce variabila ultim: ARRAY[NrSecventa] OF TipCheie.
Urmatoarea rafinare a algoritmului de distributie este cea din [4.j]:
REPEAT
SelecteazaSecventa; [4.j]
IF ultim[j]<= f0.curent.cheie THEN
*continua vechea monotonie;
CopiazaMonotonia; ultim[j]:= f0.curent.cheie
UNTIL f0.termPrelucr;
O problema evidenta este aceea ca ultim[j] se pozitioneaza numai dupa copierea primei monotonii, motiv pentru care la inceput distributia monotoniilor trebuie realizata fara inspectarea lui ultim[j].
Restul monotoniilor se distribuie conform secventei [4.k]. Se considera ca asignarea lui ultim[j] se realizeaza in procedura CopiazaMonotonia.
WHILE NOT f0.termPrelucr DO
BEGIN
SelecteazaSecventa;
IF ultim[j]<=f0.curent.cheie THEN
BEGIN
CopiazaMonotonia;
IF f0.termPrelucr THEN [4.4.k]
d[j]:= d[j]+1
ELSE
CopiazaMonotonia
END
ELSE
CopiazaMonotonia
END;
Structura algoritmului de sortare polifazica este in mare parte similara sortarii bazate pe interclasare echilibrata cu n cai:
O bucla exterioara care interclaseaza monotoniile si se executa pana cand se epuizeaza sursele;
O bucla cuprinsa in cea anterioara care interclaseaza o singura monotonie de pe fiecare secventa sursa;
Si in sfarsit o a treia bucla cuprinsa in precedenta, care selecteaza cheile si transmite elementele implicate spre secventa destinatie.
Se remarca urmatoarele diferente:
Avem o singura secventa destinatie (in loc de N/2).
In loc de a comuta N/2 secvente la fiecare trecere, acestea sunt rotite, utilizand un tablou t al indicilor secventelor.
Numarul de secvente de intrare variaza de la monotonie la monotonie; acest numar este determinat la inceputul sortarii fiecarei monotonii din valorile di ale monotoniilor fictive.
Daca di > 0, pentru toti i, atunci vor fi 'pseudo-interclasate' n -1 monotonii fictive intr-o monotonie fictiva, ceea ce presupune doar incrementarea contorului dn al secventei destinatie.
Altfel, se interclaseaza cate o monotonie de pe toate secventele care au di = 0, iar pentru restul secventelor, di se decrementeaza indicand faptul ca a fost luata in considerare o monotonie fictiva.
Se noteaza cu k1 numarul secventelor implicate intr-o interclasare.
Din cauza monotoniilor fictive, terminarea unei faze nu poate fi dedusa din conditia de sfarsit a vreuneia din secventele implicate, deoarece existenta unor monotonii fictive pe aceasta secventa face necesara continuarea interclasarii.
In schimb se poate determina usor numarul teoretic de monotonii din coeficientii ai.
Acesti coeficienti a i(k) care au fost calculati in timpul fazei de distributie vor fi recalculati in sens invers (backward) la interclasare.
Cu aceste observatii interclasarea propriu-zisa se poate formula dupa cum urmeaza [4.l]. Se presupune ca:
Toate cele n -1 secvente care contin monotoniile initiale sunt resetate
Tabloul indicilor secventelor este pozitionat conform relatiei t[i] = i
REPEAT
z:= a[n‑1]; d[n]:= 0; Rewrite(F[t[n]]);
REPEAT
k1:= 0
FOR t:= 1 TO n‑1 DO
IF d[i]>0 THEN
d[i]:= d[i]‑1
ELSE
BEGIN
k1:= k1+1; td[k1]:= t[i] [4.l]
END;
IF k1=0 THEN
d[n]:= d[n]+1
ELSE
*se interclaseaza cate o monotonie de pe
F[t[1]],,F[t[k1]];
z:= z‑1
UNTIL z=0;
Reset(F[t[n]]);
*roteste secventele in tabloul t. Calculeaza a[i]
pentru nivelul urmator;
Rewrite(F[t[n]]);
nivel:= nivel‑1
UNTIL nivel=0;
Programul de sortare polifazica este similar cu cel de sortare prin interclasare cu n cai, cu diferenta ca algoritmul de eliminare al secventelor este mai simplu.
Rotirea indicilor secventelor in tabloul indicilor, a indicilor di corespunzatori, precum si calcularea valorilor coeficientilor ai , sunt rafinate in programul urmator [4.m].
PROGRAM SortarePolifazica;
CONST n = 6; [4.m]
TYPE TipElement = RECORD
cheie: integer
END;
TipSecventa = RECORD
fisier: FILE OF TipElement;
curent: TipElement;
termPrelucr: boolean
END;
NrSecventa = 1..n;
VAR dim,aleat,tmp: integer;
eob: boolean;
buf: TipElement;
f0: TipSecventa;
F: ARRAY[NrSecventa] OF TipSecventa;
PROCEDURE List(VAR f: TipSecventa; n: NrSecventa);
VAR z: integer;
BEGIN
WriteLn(' secventa ',n); z:= 0;
WHILE NOT Eof(f.fisier) DO
BEGIN
Read(f.fisier,buf); Write(buf.cheie); z:= z+1
END;
WriteLn;
Reset(f.fisier)
END
PROCEDURE SortarePolifazica;
VAR i,j,mx,tn: NrSecventa;
k1,nivel: integer;
a,d: ARRAY[NrSecventa] OF integer;
dn,x,min,z: integer;
ultim: ARRAY[NrSecventa] OF integer;
t,td: ARRAY[NrSecventa] OF NrSecventa;
PROCEDURE SelecteazaSecventa;
VAR i: NrSecventa; z: integer;
BEGIN
IF d[j]<d[j+1] THEN
j:= j+1
ELSE
BEGIN
IF d[j]=0 THEN
BEGIN
nivel:= nivel+1; z:= a[1];
FOR i:= 1 TO n‑1 DO
BEGIN
d[i]:= z+a[i+1]‑a[i];
a[i]:= z+a[i+1]
END
END;
j:= 1
END;
d[j]:= d[j]‑1
END;
PROCEDURE CopiazaMonotonia;
VAR buf: TipElement;
BEGIN
REPEAT
buf:= f0.curent;
IF Eof(fo.fisier) THEN
f0.termPrelucr:= true
ELSE
Read(f0.fisier, f0.curent);
Write(F[t[j]].fisier,buf)
UNTIL (buf.cheie>f0.curent.cheie) OR f0.termPrelucr);
ultim[j]:= buf.cheie
END;
BEGIN
FOR i:= 1 TO n‑1 DO
BEGIN
a[i]:= 1; d[i]:= 1; Rewrite(F[i].fisier)
END;
nivel:= 1; j:= 1; a[n]:= 0; d[n]:= 0;
REPEAT
SelecteazaSecventa; CopiazaMonotonia
UNTIL f0.termPrelucr OR (j=n‑1);
WHILE NOT f0.termPrelucr DO
BEGIN
SelecteazaSecventa;
IF ultim[j]<=f0.curent.cheie THEN
BEGIN
CopiazaMonotonia;
IF f0.termPrelucr THEN
d[j]:= d[j]+1
ELSE
CopiazaMonotonia
END
ELSE
CopiazaMonotonia
END;
FOR i:= 1 TO n‑1 DO Reset(F[i]);
FOR i:= 1 TO n DO t[i]:= i;
REPEAT
z:= a[n‑1]; d[n]:= 0; Rewrite(F[t[n]]);
REPEAT
k1:= 0;
FOR i:= 1 TO n‑1 DO
IF d[i]>0 THEN
d[i]:= d[i]‑1
ELSE
BEGIN
k1:= k1+1; td[k1]:= t[i]
END;
IF k1=0 THEN
d[n]:= d[n]+1
ELSE
BEGIN
REPEAT
i:= 1; mx:= 1;
min:= F[td[1]].curent.cheie;
WHILE i<k1 DO
BEGIN
i:= i+1; x:= F[td[i]].curent.cheie;
IF x<min THEN
BEGIN
min:= x; mx:= i
END
END;
buf:= F[td[mx]].curent;
IF Eof(F[td[mx]].fisier) THEN
F[td[mx]].termPrelucr:= true
ELSE
Read(F[td[mx].fisier, F[td[mx].curent);
Write(F[t[n]].fisier,buf);
IF (buf.cheie>F[td[mx]].curent.cheie)
OR F[t[mx]].termPrelucr THEN
BEGIN
td[mx]:= td[k1]; k1:= k‑1
END
UNTIL k=0
END;
z:= z‑1
UNTIL z=0;
Reset(f[t[n]]); List(F[t[n]],t[n]);
tn:= t[n]; dn:= d[n]; z:= a[n‑1];
FOR i:= n DOWNTO 2 DO
BEGIN
t[i]:=t [i‑1]; d[i]:= d[i‑1); a[i]:= a[i‑1]‑z
END;
t[1]:= tn; d[1]:= dn; a[1]:= z;
List(f[t[1]],t[1]); nivel:= nivel‑1
UNTIL nivel=0;
END
BEGIN
dim:= 200; aleat:= 7789;
REPEAT
aleat:= (131071*aleat) MOD 2147483647;
tmp:= aleat DIV 214784; Write(f0.fisier,tmp);
dim:= dim‑1
UNTIL dim=0;
SortarePolifazica
END
Complexitatea metodelor de sortare externa prezentate nu permite formularea unor concluzii generalizatoare, cu atat mai mult cu cat evidentierea performantelor acestora este dificila. Se pot formula insa urmatoarele observatii:
Exista o legatura indisolubila intre un anumit algoritm care rezolva o anumita problema si structurile de date pe care acesta le utilizeaza, influenta celor din urma fiind uneori decisiva pentru algoritm. Acest lucru este evidentiat cu preponderenta in cazul sortarilor externe care sunt complet diferite ca mod de abordare in raport cu metodele de sortare interna.
In general, imbunatatirea performantelor unui algoritm presupune elemente foarte sofisticate, chiar in conditiile utilizarii unor structuri de date dedicate. In mod paradoxal algoritmii cu performante superioare sunt mai complicati, ocupa mai multa memorie si utilizeaza de regula structuri specializate.
|
Politica de confidentialitate |
| Copyright ©
2024 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |