Ecuatiile de tip Bernoulli[1] sunt ecuatii diferentiale de ordinul intai, care au forma generala (nu sunt ecuatii lineare)
![]() , (4.1)
, (4.1)
unde
![]() ,
, ![]() sunt functii
continue si numarul real
sunt functii
continue si numarul real ![]() . Functia (in general pozitiva)
. Functia (in general pozitiva) ![]() de clasa
de clasa ![]() care verifica
identic ecuatia (4.1) este solutie
a ecuatiei de tip Bernoulli. Deci graficul solutiilor ecuatiei
(4.1) este format din perechile ordonate de forma
care verifica
identic ecuatia (4.1) este solutie
a ecuatiei de tip Bernoulli. Deci graficul solutiilor ecuatiei
(4.1) este format din perechile ordonate de forma ![]() .
.
Vom observa ca daca ![]() ecuatia (4.1)
devine o ecuatie diferentiala lineara de ordinul intai,
neomogena, iar daca
ecuatia (4.1)
devine o ecuatie diferentiala lineara de ordinul intai,
neomogena, iar daca ![]() ecuatia (4.1)
este o ecuatie diferentiala lineara omogena.
Asadar, ecuatiile de tip Bernoulli contin, in cazurile
particulare cand
ecuatia (4.1)
este o ecuatie diferentiala lineara omogena.
Asadar, ecuatiile de tip Bernoulli contin, in cazurile
particulare cand ![]() sau
sau ![]() , ecuatiile diferentiale omogene si neomogene.
, ecuatiile diferentiale omogene si neomogene.
Presupunand ca ![]() . Daca facem schimbarea de functie
. Daca facem schimbarea de functie
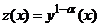 , (4.2)
, (4.2)
atunci ecuatia diferentiala nelineara (4.1) se transforma intr-o ecuatie lineara care se rezolva dupa metoda cunoscuta.
Intr-adevar, derivand relatia (4.2) obtinem
![]() , (4.3)
, (4.3)
care
substituita in (4.1) arata ca daca ![]() este o solutie a
ecuatiei Bernoulli (4.1), atunci
este o solutie a
ecuatiei Bernoulli (4.1), atunci ![]() verifica ecuatia diferentiala lineara de ordinul intai
verifica ecuatia diferentiala lineara de ordinul intai
![]() . (4.4)
. (4.4)
a). Daca ![]() , atunci
, atunci ![]() ( )
( ) ![]() nu este solutie
si deci ecuatia nu are solutii singulare.
nu este solutie
si deci ecuatia nu are solutii singulare.
b). Daca ![]() , atunci
, atunci ![]() ( )
( ) ![]() este solutie singulara.
este solutie singulara.
c). Daca ![]() , atunci
, atunci ![]() ( )
( ) ![]() este solutie particulara si
aceasta solutie se obtine din solutia generala cand
constanta de integrare ia valoarea
este solutie particulara si
aceasta solutie se obtine din solutia generala cand
constanta de integrare ia valoarea ![]() .
.
Observatie. Pentru
rezolvarea ecuatiei (4.1) putem aplica metoda
lui Bernoulli, cand se cauta solutie de forma ![]() , unde functia
, unde functia ![]() verifica
ecuatia
verifica
ecuatia ![]() , iar functia
, iar functia ![]() se determina din
conditia
se determina din
conditia ![]() (vezi ecuatii diferentiale lineare de ordinul
intai, observatia #).
(vezi ecuatii diferentiale lineare de ordinul
intai, observatia #).
Observatie. Ecuatiile de tip Bernoulli apar, de
exemplu, in studiul miscarii corpurilor in medii care opun o
rezistenta la inaintare proportionala cu viteza de
deplasare de forma ![]() , unde
, unde ![]() reprezinta viteza
corpului.
reprezinta viteza
corpului.
Exemple:
1). Sa se integreze ecuatia de tip Bernoulli
![]() ,
, ![]() .
.
Solutie. Ecuatia data este de tip
Bernoulli cu ![]() si
si ![]() . Facem schimbarea de functie
. Facem schimbarea de functie
![]() , (1)
, (1)
de unde ![]() .
.
Inlocuind aceste relatii in ecuatia
data deducem ca functia ![]() trebuie sa
verifice ecuatia diferentiala lineara neomogena
trebuie sa
verifice ecuatia diferentiala lineara neomogena
![]() . (2)
. (2)
Tehnica integrarii ecuatiei
diferentiale (2) este prezentata in . Asadar, functia ![]() este factorul
integrant corespunzator si deci solutia generala a
ecuatiei diferentiale lineare (2) are forma
este factorul
integrant corespunzator si deci solutia generala a
ecuatiei diferentiale lineare (2) are forma
![]() .
.
Datorita substitutiei (1) obtinem solutia generala a ecuatiei Bernoulli sub forma implicita
![]() , (3)
, (3)
Vom observa ca ecuatia data
este bine definita pe multimea ![]() , iar solutia stationara
, iar solutia stationara
![]() , corespunzatoare valorii y = 0, este o solutie particulara
care poate fi obtinuta din solutia generala (3) daca
luam pentru constanta
, corespunzatoare valorii y = 0, este o solutie particulara
care poate fi obtinuta din solutia generala (3) daca
luam pentru constanta ![]() valoarea
valoarea ![]() .
.
2). Sa se integreze ecuatia de tip Bernoulli
![]() ,
, ![]() , cu conditia initiala
, cu conditia initiala ![]() .
.
Solutie. Avem: ![]() ,
, ![]() ,
, ![]() . Potrivit relatiei (4.2), se face schimbarea de
functie
. Potrivit relatiei (4.2), se face schimbarea de
functie
![]() . (1)
. (1)
Deci, ![]() si atunci
functia
si atunci
functia ![]() verifica
ecuatia lineara neomogena
verifica
ecuatia lineara neomogena
![]() ,
, ![]() . (2)
. (2)
Daca presupunem ![]() atunci ecuatia (2),
prin integrare, conduce la solutia generala sub forma explicita
atunci ecuatia (2),
prin integrare, conduce la solutia generala sub forma explicita ![]() ,
, ![]() . Pentru a obtine solutia generala a
ecuatiei Bernoulli va trebui sa substituim expresia lui
. Pentru a obtine solutia generala a
ecuatiei Bernoulli va trebui sa substituim expresia lui ![]() in relatia (1).
Avem
in relatia (1).
Avem
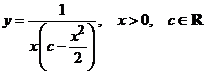 . (3)
. (3)
Retinem pentru ecuatia data
si solutia particulara
de forma ![]() , ( )
, ( ) ![]() , solutie care se obtine din solutia
generala pentru
, solutie care se obtine din solutia
generala pentru ![]() .
.
Deoarece se da punctul initial ![]() si se cere
solutia ecuatiei care trece prin acest punct, va trebui sa inlocuim,
in solutia generala (3), valorile
si se cere
solutia ecuatiei care trece prin acest punct, va trebui sa inlocuim,
in solutia generala (3), valorile ![]() . Deducem
. Deducem ![]() si atunci solutia
problemei Cauchy considerata are forma
si atunci solutia
problemei Cauchy considerata are forma
![]() .
.
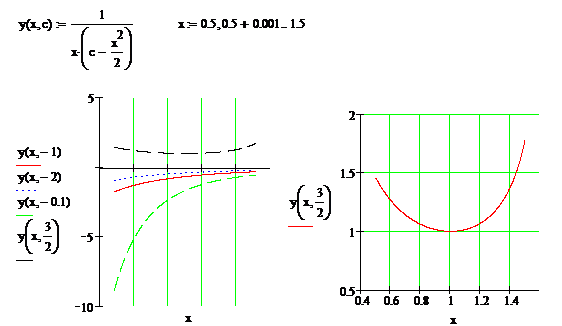
Graficul solutiei, reprezentat pe figura
din dreapta este continut in ![]() . Pe figura din partea stanga sunt reprezentate
graficele solutiilor pentru diferite valori date constantei
. Pe figura din partea stanga sunt reprezentate
graficele solutiilor pentru diferite valori date constantei ![]()
3). Integrati ecuatiile diferentiale
a) ![]() ,
, ![]() ;
; ![]() ;
;
b) ![]() ,
, ![]() , cu conditia
initiala
, cu conditia
initiala ![]() ;
;
c) 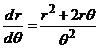 ,
, ![]() ;
; ![]() .
.
Solutii: a). Ecuatia data este de tip
Bernoulli cu ![]() ,
, ![]() . Facem schimbarea de functie
. Facem schimbarea de functie ![]() . Avem
. Avem ![]() si ecuatia
data se transforma in ecuatia lineara neomogena de
ordinul intai
si ecuatia
data se transforma in ecuatia lineara neomogena de
ordinul intai
![]() ,
, ![]() ,
, ![]() . (1)
. (1)
Pentru integrare deducem ca factorul
integrant este ![]() , iar solutia generala a ecuatiei lineare (1)
are forma
, iar solutia generala a ecuatiei lineare (1)
are forma
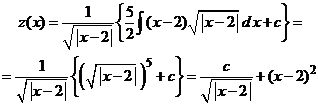
Revenind la functia ![]() , rezulta ca solutia generala a
ecuatiei Bernoulli are forma (vezi Fig.#)
, rezulta ca solutia generala a
ecuatiei Bernoulli are forma (vezi Fig.#)
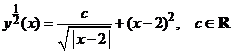 .
.
Pentru aceasta
ecuatie de tip Bernoulli retinem si solutia singulara ![]() ,
, ![]() .
.
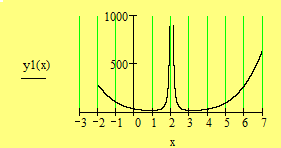
Figura
1. Graficul solutiei pentru ![]() .
.
b) Ecuatia poate fi scrisa sub forma normala
![]() ,
, ![]() . (1)
. (1)
Asadar, ecuatia este de tip
Bernoulli cu ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Cu schimbarea de functie,
. Cu schimbarea de functie,
![]() , (2)
, (2)
ecuatia data se transforma in ecuatia lineara neomogena
![]() ,
, ![]() . (3)
. (3)
Solutia generala a ecuatiei (3) este
![]() ,
, ![]() ,
, ![]() . (4)
. (4)
 Notand cu
Notand cu ![]() , putem scrie solutia (4) sub forma
, putem scrie solutia (4) sub forma
![]() ,
, ![]() ,
, ![]() (5)
(5)
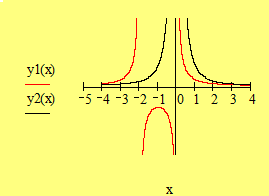
si datorita schimbarii de functie (2), din (5) deducem ca solutia generala a ecuatiei Bernoulli are forma (vezi Fig. 2)
![]() ,
, ![]() ,
, ![]() . (6)
. (6)
Functia ![]() , este o solutie
particulara a ecuatiei (1) care se obtine din (6) pentru
, este o solutie
particulara a ecuatiei (1) care se obtine din (6) pentru
Figura2. valoarea
![]() .
.
Din familia curbelor
integrale (6) retinem pe aceea care trece prin punctul ![]() daca cerem ca
daca cerem ca ![]() si
si ![]() sa verifice
expresia (6). Deducem
sa verifice
expresia (6). Deducem ![]() . Deci solutia problemei Cauchy (3.b) este
. Deci solutia problemei Cauchy (3.b) este
![]() . (7)
. (7)
c) Ecuatia este echivalenta cu ecuatia diferentiala scrisa sub forma normala
![]() ,
,
care
este de tip Bernoulli cu ![]() . Procedand ca mai inainte obtinem solutia generala de forma
. Procedand ca mai inainte obtinem solutia generala de forma
![]()
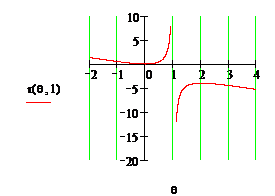 si
solutia
particulara
si
solutia
particulara ![]() ( )
( ) ![]() .
.
In figura alaturata
sunt reprezentate solutiile ecuatiei pentru ![]() , pentru
, pentru ![]() , respectiv pentru
, respectiv pentru ![]()
Observatie. Daca se cunosc doua solutii particulare ale ecuatiei Bernoulli, atunci fara nici o cuadratura, se pot determina solutiile ecuatiei Bernoulli.
Intr-adevar, folosind schimbarea de
functie (4.2), deducem ca daca ![]() si
si ![]() sunt solutii
particulare ale ecuatiei Bernoulli, atunci
sunt solutii
particulare ale ecuatiei Bernoulli, atunci ![]() si respectiv
si respectiv ![]() , sunt solutii ale ecuatiei diferentiale
lineare (4.4). Datorita linearitatii acestei ecuatii
rezulta ca diferenta
, sunt solutii ale ecuatiei diferentiale
lineare (4.4). Datorita linearitatii acestei ecuatii
rezulta ca diferenta ![]() este solutie a
ecuatiei omogene asociate. Cum solutiile ecuatiei diferentiale
omogene formeaza un spatiu vectorial unidimensional, atunci
solutia generala a ecuatiei lineare neomogene are forma
este solutie a
ecuatiei omogene asociate. Cum solutiile ecuatiei diferentiale
omogene formeaza un spatiu vectorial unidimensional, atunci
solutia generala a ecuatiei lineare neomogene are forma ![]() . Revenind la schimbarea de functie deducem ca functia
. Revenind la schimbarea de functie deducem ca functia
![]() ,
,
este solutia generala a ecuatiei Bernoulli.
Caderea libera pe verticala a corpurilor
Un corp M, avand masa ![]() , situat la inaltimea
, situat la inaltimea ![]() fata de
suprafata Pamantului, este lasat sa cada pe
verticala sub actiunea greutatii, intr-un mediu rezistent,
fara viteza initiala. Stiind ca rezistenta
mediului este proportionala cu patratul vitezei, sa se
determine viteza corpului, in cadere, la momentul
fata de
suprafata Pamantului, este lasat sa cada pe
verticala sub actiunea greutatii, intr-un mediu rezistent,
fara viteza initiala. Stiind ca rezistenta
mediului este proportionala cu patratul vitezei, sa se
determine viteza corpului, in cadere, la momentul ![]() , cat si distanta parcursa dupa scurgerea
a
, cat si distanta parcursa dupa scurgerea
a ![]() secunde.
secunde.
|
Caderea libera a corpurilor. |
Fie ![]() spatiul parcurs
pana la momentul
spatiul parcurs
pana la momentul ![]() . Legea de miscare a lui Newton, conform careia
punctul material de masa
. Legea de miscare a lui Newton, conform careia
punctul material de masa ![]() , care evolueaza sub actiunea unei forte
, care evolueaza sub actiunea unei forte ![]() se
desfasoara astfel incat
se
desfasoara astfel incat
![]() , (1)
, (1)
unde
![]() este acceleratia.
este acceleratia.
Pentru a putea descrie
evolutia punctului material ![]() alegem ca sistem de
coordonate (miscarea are loc pe verticala) dreapta reala
alegem ca sistem de
coordonate (miscarea are loc pe verticala) dreapta reala ![]() si fie originea
in punctul situat la inaltimea
si fie originea
in punctul situat la inaltimea ![]() de la suprafata
pamantului si
de la suprafata
pamantului si ![]() spatiul parcurs
pana la momentul
spatiul parcurs
pana la momentul ![]() .
.
i). Conform legii de miscare a lui Newton, in cazul in care se neglijeaza rezistenta aerului putem scrie ecuatia diferentiala
![]() , (2)
, (2)
cu conditiile initiale (pozitia si viteza initiala)
![]() , (3)
, (3)
Atunci, functia ![]() , unde
, unde ![]() sunt constante de
integrare care se determina din conditiile initiale:
sunt constante de
integrare care se determina din conditiile initiale:
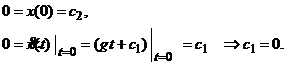 (4)
(4)
Asadar, miscarea descrisa de ecuatia diferentiala (2), cu conditiile initiale (3), are loc dupa "traiectoria"
![]() . (5)
. (5)
Asadar, relatia ![]() , care defineste solutia generala a ecuatiei
diferentiale (2), supusa la conditiile initiale,
, care defineste solutia generala a ecuatiei
diferentiale (2), supusa la conditiile initiale, ![]() , conduce la solutia
, conduce la solutia
![]() ;
; 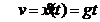 .
.
La momentul ![]() , cand corpul atinge suprafata Pamantului avem:
, cand corpul atinge suprafata Pamantului avem:
din
![]() , deducem
, deducem ![]() , de unde obtinem
, de unde obtinem ![]() sau
sau 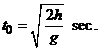 .
.
Viteza pe care o atinge corpul ![]() la intalnirea cu solul
va fi
la intalnirea cu solul
va fi
![]()
Procedeul obtinerii legii de miscare a corpurilor
a). Se determina toate fortele care actioneaza asupra corpului (sistemului) aflat in studiu;
b). Se aleg axele sistemului de coordonate
corespunzatoare spatiului in care are loc miscarea (in mecanica
clasica spatiul este euclidian,
izotrop si omogen: spatiul ![]() sau in planul
sau in planul ![]() , sau pe dreapta reala
, sau pe dreapta reala ![]() ). Este important sa specificam ca sistemul de
coordonate ales trebuie sa fie sistem
de referinta inertial, determinat prin luarea in calcul a
acceleratiei datorita rotatiei Pamantului in jurul axei
si a miscarii Pamantului in jurul Soarelui;
). Este important sa specificam ca sistemul de
coordonate ales trebuie sa fie sistem
de referinta inertial, determinat prin luarea in calcul a
acceleratiei datorita rotatiei Pamantului in jurul axei
si a miscarii Pamantului in jurul Soarelui;
b). Aplicam legea a doua a lui Newton (lege care se aplica numai in sisteme inertiale, adica in sisteme de coordonate care au proprietatile: a) la orice moment de timp, toate legile naturii sunt aceleasi in toate sistemele inertiale; b) toate sistemele de coordonate care se misca uniform si rectiliniu in raport cu un sistem inertial sunt inertiale):
![]() , (6)
, (6)
unde
![]() este impulsul (forta motrice) a
sistemului. Atunci legea lui Newton se poate scrie
este impulsul (forta motrice) a
sistemului. Atunci legea lui Newton se poate scrie
![]() . (7)
. (7)
In general fortele ![]() nu depind de
nu depind de ![]() , ele depind in cele mai numeroase cazuri de timpul
, ele depind in cele mai numeroase cazuri de timpul ![]() si de viteza
si de viteza ![]() . Asadar, putem scrie
. Asadar, putem scrie ![]() .
.
Daca forta ![]() depinde numai de
depinde numai de ![]() , putem introduce, prin definitie, functia potential
, putem introduce, prin definitie, functia potential ![]() astfel incat
astfel incat
![]() , sau
, sau ![]() (8)
(8)
Semnul minus din aceasta formula
este ales astfel incat energia potentiala sa fie cu atat mai
mare cu cat distanta ![]() a punctul material
fata de suprafata Pamantului este mai mare (vezi
relatia (2), unde se ia
a punctul material
fata de suprafata Pamantului este mai mare (vezi
relatia (2), unde se ia ![]() ).
).
Vom observa ca relatia (8)
arata cum energia potentiala (functia de potential ![]() ) determina pe
) determina pe ![]() .
.
Folosind functia de potential atunci legea de miscare a lui Newton (1) devine
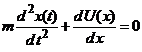 .
.
Aceasta relatie arata ca
in timpul miscarii, expresia 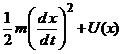 ramane
constanta.
ramane
constanta.
Intr-adevar, deoarece ![]() atunci prin derivarea
in raport cu timpul in expresia de mai sus, avem
atunci prin derivarea
in raport cu timpul in expresia de mai sus, avem
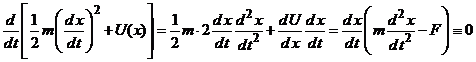 .
.
Deoarece 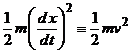 reprezinta energia cinetica a sistemului,
este natural sa definim functia
reprezinta energia cinetica a sistemului,
este natural sa definim functia ![]() ca energia potentiala determinata
de forta
ca energia potentiala determinata
de forta ![]() si
si 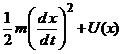 ca energia
totala a sistemului.
ca energia
totala a sistemului.
Asadar, am demonstrat
ca energia totala a sistemului in miscare, descris de
relatia ![]() , este constanta. Acesta afirmatie constituie principiul conservarii energiei.
, este constanta. Acesta afirmatie constituie principiul conservarii energiei.
Fie ![]() o solutie a
ecuatiei diferentiale
o solutie a
ecuatiei diferentiale ![]() , unde functia
, unde functia ![]() nu depinde explicit de
nu depinde explicit de
![]() si
si ![]() . Daca
. Daca ![]() este o primitiva
a functiei
este o primitiva
a functiei ![]() , atunci cantitatea
, atunci cantitatea ![]() , numita energia
totala a sistemului, este constanta in timp, adica
, numita energia
totala a sistemului, este constanta in timp, adica ![]() . Intr-adevar, avem
. Intr-adevar, avem
![]() .
.
Cantitatea ![]() se numeste energia potentiala a sistemului in
miscare descris de ecuatia
se numeste energia potentiala a sistemului in
miscare descris de ecuatia ![]() . In cazul caderii pe verticala avem
. In cazul caderii pe verticala avem ![]() .
.
In continuare luam in discutie caderea libera a corpului, cand miscarea se desfasoara intr-un mediu rezistent[3].
ii). Vom presupune ca punctul material ![]() intampina o
rezistenta a aerului (rezistenta mediului) la inaintare de forma
intampina o
rezistenta a aerului (rezistenta mediului) la inaintare de forma
![]() , avand marimea
, avand marimea ![]() , unde
, unde ![]() reprezinta viteza
corpului.
reprezinta viteza
corpului.
Ecuatia diferentiala care descrie miscarea corpului are forma
![]() (6)
(6)
cu conditiile initiale:
deplasare
initiala ![]() ;
;
viteza
initiala ![]() (adica
evolutia miscarii are loc fara viteza
initiala);
(adica
evolutia miscarii are loc fara viteza
initiala);
Ecuatia (6) se scrie sub forma echivalenta
![]() (7)
(7)
care poate fi privita ca o ecuatie cu variabile separabile.
In ipoteza ca ![]() , putem separa variabilele si avem
, putem separa variabilele si avem
![]() ,
, ![]() . (8)
. (8)
Luand cate o primitiva in ambii membri ai ecuatiei (8), rezulta
![]() ,
,
sau, inca,
![]() . (9)
. (9)
Cu notatia ![]() , putem scrie
, putem scrie ![]() sau
sau
![]() , (10)
, (10)
unde
semnul ![]() este acelasi cu
semnul expresiei
este acelasi cu
semnul expresiei ![]() . Asadar, viteza de deplasare
. Asadar, viteza de deplasare ![]() a punctului material
este solutia generala a ecuatiei (7) si are forma
a punctului material
este solutia generala a ecuatiei (7) si are forma
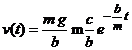 (11)
(11)
In cazul cand analizam unele situatii
concrete marimile ![]() si
si ![]() sunt cunoscute. Atunci
constanta
sunt cunoscute. Atunci
constanta ![]() , din solutia generala (11), se determina
cunoscand viteza initiala. Din conditia initiala (7) , obtinem
, din solutia generala (11), se determina
cunoscand viteza initiala. Din conditia initiala (7) , obtinem ![]() , de unde
, de unde ![]() si avem
si avem
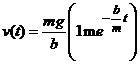 . (12)
. (12)
In cazul general cand
conditia initiala (7)2 are forma ![]() , atunci solutia generala (11) devine
, atunci solutia generala (11) devine
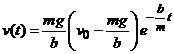 . (13)
. (13)
Studiul se face utilizand, de obicei,
sistemul de unitati de masura ![]() , metru-kilogram-secunda.
, metru-kilogram-secunda.
Asimptota orizontala pentru viteza ![]() se numeste viteza finala a punctului
material si viteza
se numeste viteza finala a punctului
material si viteza ![]() , este un echilibru
stabil pentru ecuatia
autonoma (pag. 25 Edif.).
, este un echilibru
stabil pentru ecuatia
autonoma (pag. 25 Edif.).
Din
![]() ,
, ![]() ,
,
deducem solutia
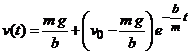 .
.
Luand ![]() si
si ![]() avem
avem
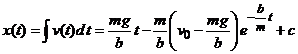 .
.
Folosind prima conditie
initiala (7), deducem pentru constanta ![]() , valoarea
, valoarea
![]() .
.
Atunci solutia problemei initiale
(6), (7), cu ![]() , are forma
, are forma
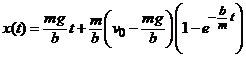 .
.
Pentru ![]() , pozitia
, pozitia ![]() tinde catre
asimptota (solutie particulara)
tinde catre
asimptota (solutie particulara)
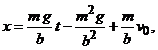 cand
cand ![]() .
.
Cazuri particulare:
1). ![]()
2). Cazul parasutistului: ![]() ;
; ![]() . (pg. 119 E.d.)
. (pg. 119 E.d.)
Reprezentati graficele solutiilor
pentru ![]() si cateva valori
initiale ale vitezei.
si cateva valori
initiale ale vitezei.
ii). Vom presupune cazul cand rezistenta ![]() a aerului are
marimea
a aerului are
marimea ![]() .
.
Atunci, ecuatia de miscare are forma
![]() . (14)
. (14)
Impunem conditiile initiale: ![]() (deplasarea
initiala);
(deplasarea
initiala); ![]() (fara
viteza initiala).
(fara
viteza initiala).
Pentru a reduce ordinul ecuatiei (14) cu
o unitate vom introduce functia ![]() . Avem
. Avem
![]() (15)
(15)
Introducand notatia ![]() , atunci ecuatia devine
, atunci ecuatia devine
![]() (16)
(16)
Daca ![]() , putem separa variabilele si avem
, putem separa variabilele si avem
![]() .
.
Luand
cate o primitiva in ambii membrii ai acestei egalitati,
obtinem ![]() ,
, ![]() . Folosind conditia initiala
. Folosind conditia initiala ![]() , deducem
, deducem ![]() . Asadar, solutia are expresia
. Asadar, solutia are expresia
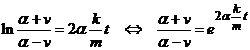 ,
,
sau
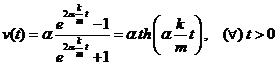 .
.
Cum ![]() , putem scrie
, putem scrie
![]() ,
,
de unde obtinem
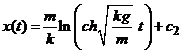 .
.
Deoarece ![]() si
si ![]() , ( )
, ( ) ![]() si
si ![]() , atunci traiectoria miscarii are forma
, atunci traiectoria miscarii are forma
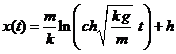 .
.
Familia
matematicienilor Bernoulli, originara din Anvers, s-a refugiat la Bale la
sfarsitul sec. al XVI-lea. Se cunosc peste 120 de descendenti ai
acestei familii care au fost oameni de stiinta. Johan Bernoulli (1667-1748), matematician
elvetian, profesor la Universitatea din Bassel (unde a avut elevi pe L.
Euler, A. Clairaut), membru al Academiei de Stiinte din Paris si
al Academiei de Stiinte din Petersburg. Ecuatia lui Bernoulli, ecuatie propusa spre rezolvare de fratele
acestuia, James Bernoulli in 1695, este rezolvata de Johan prin metoda Bernoulli (![]() ). In 1696 Gottfried Leibniz a aratat ca
ecuatia de tip Bernoulli poate fi redusa la o ecuatie
lineara daca se face schimbarea
). In 1696 Gottfried Leibniz a aratat ca
ecuatia de tip Bernoulli poate fi redusa la o ecuatie
lineara daca se face schimbarea ![]() .
.
Caderea pe verticala a corpurilor, de la o inaltime nu prea
mare, a fost descrisa experimental de Galileo Galilei (1564-1642) si
este formulata matematic prin ecuatia diferentiala ![]() (ecuatia arata
ca acceleratia corpurilor ramane constanta).
(ecuatia arata
ca acceleratia corpurilor ramane constanta).
Nu
exista o lege generala care modeleaza actiunea
rezistentei aerului asupra corpului deoarece aceste forte depind de
viteza corpului, de densitatea aerului, forma corpului etc. De exemplu,
forta de rezistenta a aerului se alege proportionala
cu viteza corpului: ![]() , unde
, unde ![]() este versor avand
sensul acceleratiei gravitationale
este versor avand
sensul acceleratiei gravitationale ![]() , constanta b este
pozitiva si depinde de forma corpului si de densitatea aerului,
semnul minus arata ca rezistenta se opune miscarii.
, constanta b este
pozitiva si depinde de forma corpului si de densitatea aerului,
semnul minus arata ca rezistenta se opune miscarii.
|
Politica de confidentialitate |
| Copyright ©
2024 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |