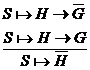Logica propozitiilor
Baza cunoasterii o formeaza notiunile. Exemple de notiuni sunt numarul, operatiile, obiectele.
Relatiile dintre notiuni sunt judecatile.
Se numeste propozitie o expresie verbala a unei judecati despre care se poate spune daca este adevarata sau falsa. Pentru a decide daca o propozitie este adevarata ea trebuie plasata intr-un univers U al discursului.
O forma propozitionala este o propozitie P(x) in care apare variabila x element al universului U.
Exemple
In universul U al domnitorilor Moldovei, forma propozitionala:
"x este fiul predecesorului sau"
-este adevarata pentru x = Petru Rares
-este falsa pentru x = Alexandru Lapusneanu
In universul U al cartilor din biblioteca , forma propozitionala:
" x este o carte scrisa de Mircea Eliade "
-este adevarata pentru x = Istoria religiilor
-este falsa pentru x = Pseudo-Kynegheticos.
Pentru a
individualiza o submultime 
, este suficient sa precizam o forma
propozitionala P(x) in U. Acestei forme i se
asociaza multimea elementelor 
pentru care forma propozitionala este
adevarata.
1. Principiile din logica matematica
Principiul celor doua valori. Vom considera ca propozitiile pot fi doar adevarate sau false. Acest principiu se stipuleaza in felul urmator:
a) Principilul tertiului exclus: O propozitie este sau adevarata, sau falsa, alta varianta nu exista.
b) Principiul noncontradictiei: O propozitie nu poate fi in acelasi timp si adevarata si falsa.
2. Formarea propozitiilor
Propozitiile elementare sunt de forma : " S este P". Interpretarea acestei propozitii: subiectul S este numele predicativ P. De exemplu: "Casa este verde". Aici S = "casa" iar P = "verde".
Propozitiile elementare se leaga prin conectivele logice care se mai chema si functori logici sau conectori logici:
|
Functorul |
Simbolul |
Numele operatiei |
|
non |
- |
Negatia |
|
si |
|
Conjunctia |
|
sau |
|
Disjunctia |
|
Daca atunci |
|
Implicatia |
|
Daca si numai daca |
|
Echivalenta |
Utilizand acesti functori obtinem propozitii compuse.
Exemplu:
Fie
propozitiile p :
"casa este verde" q: " gardul
este stricat". p
q este o noua propozitie : "casa este verde si gardul este stricat".
Valoarea unei propozitii
Valoarea unei propozitii asociaza numarul 1 propozitiilor adevarate si 0 propozitiilor false.
v(p)=1 , daca propozitia este adevarata
v(p)=0 , daca propozitia este falsa.
4. Scheme de construire a unor propozitii din alte propozitii
Pornind de la
propozitia p se obtine propozitia 
care este
adevarata cand p este falsa. Celor doua
propozitii le putem atasa un tabel al valorilor de adevar:
Tabela de adevar pentru negatie:
|
p |
|
|
0 |
1 |
|
1 |
0 |
Daca p si q sunt doua propzitii (sau doua forme propozitionale de aceeiasi variabila), atunci
este o noua
propozitie, adevarata atunci cand si p si q
sunt adevarate
este o noua
propozitie, adevarata atunci cand este adevarata cel
putin una dintre cele doua propozitii.
Tabela de adevar pentru conjunctie si disjunctie:
|
p |
q |
|
|
|
0 |
0 |
0 |
0 |
|
0 |
1 |
0 |
1 |
|
1 |
0 |
0 |
1 |
|
1 |
1 |
1 |
1 |
Obsevatie.
Sa consideram P(x), o forma propozitionala, si A multimea elementelor pentru care P(x) este adevarata. Sa notam cu B multimea pe care Q(x) este adevarata. Ca in figura 1. am reprezentat prin diagrame Venn multimile elementelor si valorile de adevar ale propozitiilor. Se vede imediat ca:
este
adevarata pe multimea 
este
adevarata pentru 
este
adevarata pentru 
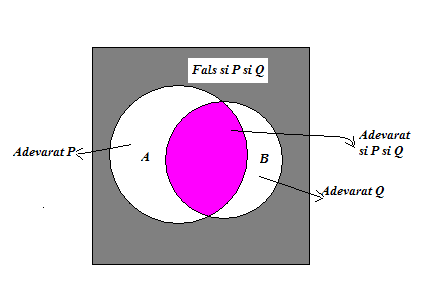
Fig.1.
Implicatia 
: este o propozitie falsa cand p este
adevarata si q este falsa.
Tabela de adevar pentru implicatie si echivalenta
|
p |
q |
|
|
|
|
0 |
0 |
1 |
1 |
1 |
|
0 |
1 |
1 |
1 |
0 |
|
1 |
0 |
0 |
0 |
0 |
|
1 |
1 |
0 |
1 |
1 |
Pe de alta
parte, propozitia 
este
adevarata indiferent de valorile propozitiilor p si q,
asa cum rezulta din ultima coloana a tabelului de mai jos.
|
p |
q |
|
|
|
|
0 |
0 |
1 |
1 |
1 |
|
0 |
1 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
1 |
|
1 |
1 |
0 |
1 |
1 |
5. Construirea multimii propozitiilor.
Fie 
o multime nevida de propozitii elementare. Aplicatia de valuare 
este o functie
surjectiva care atasaza unei propozitii valoarea sa de
adevar.
Cu ajutorul
functorilor 
se extinde la
multimea tuturor propozitiilor P , iar functia de valuare
se extinde la 
.
Putem defini inductiv aceasta extindere. Extinderea lui
(i) 
(ii) daca se dau expresiile 
, atunci 
sunt expresii .
Extinderea lui v
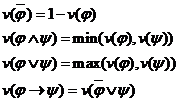
(iii) Multimea P este formata numai din elementele definite prin (i)si (ii).
Am obtinut
in acest mod o algebra generata de adica 
.
Elementele din P se numesc propozitii. sunt propozitii
compuse obtinute din propozitiile elementare aplicand (ii).
Din cele discutate pana acum putem compune tabelul valorilor de adevar pentru functorii descrisi mai sus.
|
p |
q |
|
|
|
|
|
|
0 |
0 |
1 |
0 |
0 |
1 |
1 |
|
0 |
1 |
1 |
0 |
1 |
1 |
0 |
|
1 |
0 |
0 |
0 |
1 |
0 |
0 |
|
1 |
1 |
0 |
1 |
1 |
1 |
1 |
6. Ierarhizarea functorilor logici
Functorii logici sunt aplicati pe rand in expresii
respectand urmatoarea ordine de prioritate: 
. Ordinea aplicarii functorilor poate fi modificata
cu ajutorul parantezelor.
Functia de adevar pentru expresii este, asa
cum am spus, . Doua
expresii sunt semantic
echivalente, 
, daca 
.
Se numeste
tautologie o expresie universal valabila , adica pentu care 
.
Exemple de tautologii.
1) 
este o tautologie.
Demonstratia o vom face construind un tabel al valorilor de adevar.
|
p |
q |
|
|
|
0 |
0 |
1 |
1 |
|
0 |
1 |
0 |
1 |
|
1 |
0 |
1 |
1 |
|
1 |
1 |
1 |
1 |
Ultima coloana arata ca valoare propozitiei este 1 indiferent de valorile propozitiilor elementare.
2) 
este o tautologie.
Intr-adevar, urmarind tabelul vedem ca valorile acestei
propozitii sunt 1 indiferent de valorile variabilelor.
|
p |
q |
|
|
|
|
|
|
0 |
0 |
1 |
1 |
1 |
1 |
1 |
|
0 |
1 |
1 |
0 |
1 |
1 |
1 |
|
1 |
0 |
0 |
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
0 |
1 |
0 |
1 |
7. Formule propozitionale
Multimii propozitiilor elementare , i se adauga multimea variabilelor
propozitionale 
. Astfel,
multimea 
si formulele
obtinute cu functorii alcatuiesc
algebra 
, generata de F. Daca 
este o formula
propozitionala care depinde de variabilele 
, notam formula propozitionala cu 
.
Inlocuind variabilele cu propozitiile 
se obtine o
noua propozitie 
.
O formula se numeste
tautologie, sau lege logica sau formula identic adevarata,
daca 
, propozitia este
adevarata.
Decidem daca este o tautologie pe
baza tabelului valorilor pe care le poate lua conform cu 
.
Daca 
este o tautologie,
atunci este o absurditate.
Daca nu este nici
tautologie, nici absurditate, atunci se numeste formula
realizabila.
Daca este o tautologie,
atunci valoarea sa de adevar 
depinde numai de , nu si de .
Exemple de tautologii.
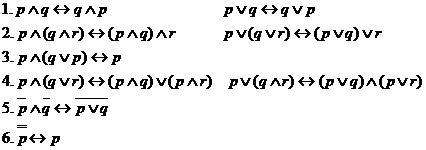
Ca exercitiu, sa demonstram
tautologia 
. Construim in acest scop tabelul valorilor de adevar
|
p |
q |
|
|
|
|
0 |
0 |
0 |
0 |
1 |
|
0 |
1 |
1 |
0 |
1 |
|
1 |
0 |
1 |
1 |
1 |
|
1 |
1 |
1 |
1 |
1 |
Demonstratia tautologiei 
decurge in felul
urmator
|
p |
q |
|
|
|
|
|
|
0 |
0 |
1 |
1 |
1 |
1 |
1 |
|
0 |
1 |
1 |
0 |
0 |
0 |
1 |
|
1 |
0 |
0 |
1 |
0 |
0 |
1 |
|
1 |
1 |
0 |
0 |
0 |
0 |
1 |
Demonstratia principiului tertiului
exclus 
si respectiv 
:
|
p |
|
|
|
|
0 |
1 |
1 |
1 |
|
1 |
0 |
1 |
1 |
Alte tautologii
Exercitiu.
Sa se demonstreze tautologia 
Rezolvare.
|
p |
q |
r |
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
1 |
|||
|
1 |
0 |
0 |
0 |
0 |
1 |
|||
|
1 |
0 |
0 |
0 |
0 |
1 |
|||
|
1 |
0 |
0 |
0 |
0 |
1 |
|||
|
0 |
0 |
0 |
0 |
0 |
1 |
|||
|
1 |
1 |
0 |
1 |
1 |
1 |
|||
|
1 |
1 |
1 |
0 |
1 |
1 |
|||
|
1 |
1 |
1 |
1 |
1 |
1 |
8. Scheme cu contacte
Utilizarea logicii matematice in analiza si sinteza circuitelor electrice si electronice dateaza din primii ani ai proiectarii mecanismelor automate si apoi a calculatoarelor. Gr.C.Moisil s-a preocupat de teoria algebrica a mecanismelor automate, publicand in 1959 un curs asupra acestor probleme.
Intr-o schema distingem elementele de comanda (contacte normal deschise sau normal inchise), elementele intermediare si elementele de executie (becuri, dispozitive de semnalizare etc).
Vom nota in continuare cu litere mici a,b,,z,
contactele normal inchise si cu 
contactele normal
deschise.
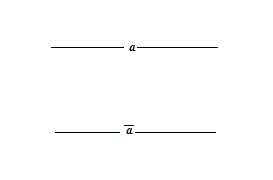
Fig. 2. Contacte normal inchise si normal deschise
Dipoli cu contacte
a) Circuitul deschis, respectiv circuitul
inchs formeaza un dipol 
cu contacte
b) Contactele normal inchise si normal
deschise sunt dipoli cu contacte
c) Daca 
sunt dipoli , atunci dipolii obtinuti prin montarea in serie
sau paralel a dipolilor , sunt dipoli cu contacte
Formulele de structura a unei scheme .
a,b,,z, contactele normal inchise
contactele normal
deschise
X,,Z relee
U,W lampi
simbol pentru montarea in serie
simbol pentru montare in paralel
Pentru schema de mai jos
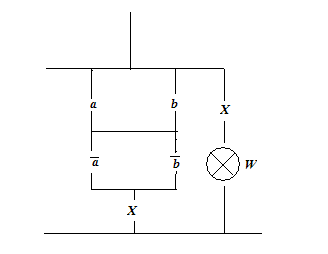
Fig.
formula de structura este 
9. Functia de lucru a unui dipol cu contacte
Se considera o variabila k indicand starea de functionare a unui dipol. Daca k = 1, dipolul conduce, daca k = 0, dipolul nu conduce.
Conductibilitatea dipolului din figura de mai jos
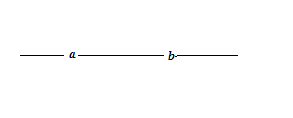
Fig. 4.
Poate fi stabilita utlizand tabelul urmator:
|
a |
b |
|
|
0 |
0 |
0 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
Conductibilitatea dipolului din figura 5
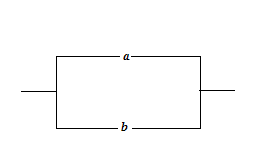
Fig. 5.
Poate fi stabilita din tabelul
|
a |
b |
|
|
0 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
1 |
Pentru dipolul din figua 6
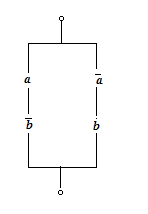
Fig. 6.
Formula de structura este
Functia de lucru a dipolului este data in tabelul urmator
|
a |
b |
|
|
|
|
0 |
0 |
0 |
0 |
0 |
|
0 |
1 |
0 |
1 |
1 |
|
1 |
0 |
1 |
0 |
1 |
|
1 |
1 |
0 |
0 |
0 |
10. Prima problema de analiza
Prima problema de analiza cere sa se determine valoarea functiei de lucru a unui dipol.
Exemplu. Se da dipolul de mai jos:
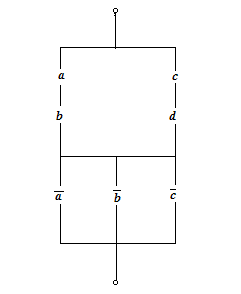
Fig. 7.
Se pune problema de a stabilii daca pentru a = b = 1, c = d = 0 dipolul conduce ?
Formula de
structura a dipolului este 
Functia de lucru primeste pentru a = b = 1, c = d = 0 valoarea
, deci dipolul conduce.
Probleme
Sa se scrie formulele de structura pentru schemele de mai jos.
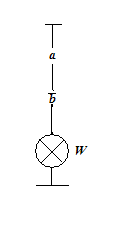
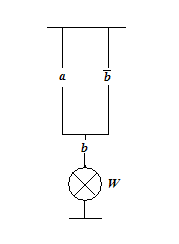
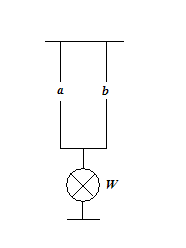
Problema 1. Problema 2. Problema
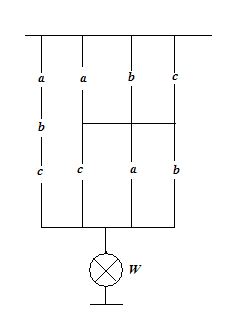
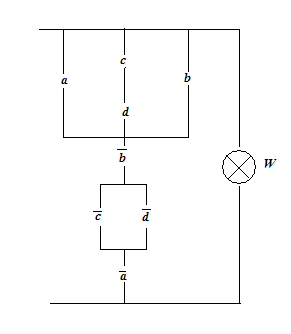
Problema 4 Problema 5
Solutia problemei 1: 
Solutia problemei 2: 
Solutia problemei 3: 
Solutia problemei 4: 
Solutia problemei 5: 
11. Inferete logice
Inferenta logica este o metoda de a obtine noi propozitii adevarate din propozitii despre care s-a stabilit deja ca sunt adevarate.
Orice tautologie conduce la o regula de inferenta.
Conditiile de aplicare a unei reguli precizeaza premisele inferentei si apoi concluzia. Se utilizeaza notatia
Daca S este un sistem de reguli de inferenta se introduce relatia
"A
poate fi dedus din S", notata 
.
Exemple
1) 
Inferenta corespunzatoare este urmatoarea:
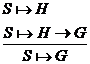
Explicand cu cuvinte, notatia de mai sus
inseamna: daca H
poate fi dedus din S si 
poate fi dedus din S,
atunci G poate fi dedus din S.
2) 
Aceasta tautologie se poate scrie ca un lant de inferente
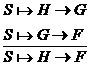
Citim astfel premisele: 
, implicatia poate fi dedusa
din S si la randul ei, implicatia 
poate fi
dedusa din S .
Concluzia este ca implicatia
poate fi dedusa
din S.
Tautologia 
poate fi scrisa
ca regula contrapozitiei:
Tautologia
poate fi scrisa
ca principiul contradictiei in felul urmator
