
MODELE PARAMETRICE SI MODELE NEPARAMETRICE
In oricare din metodele de caracterizare matematica a sistemelor liniare, prezentate anterior, modelele pot fi sub forma parametrica - daca forma analitica a modelului are o structura data, descrisa complet printr-un numar finit de parametri - sau sub forma neparametrica - daca modelul matematic este definit prin intermediul unor (unei) functii reprezentate grafic.
MODELE PARAMETRICE
Fie un sistem in descriere functionala, avand intrarea u(t) si iesirea y(t). Un model parametric tipic este ecuatia diferentiala intrare-iesire:
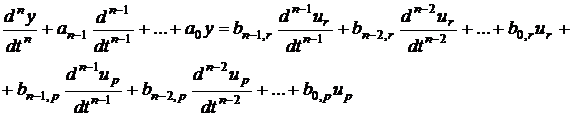 (1)
(1)
Cunoscand setul de 2n parametri, reprezentand coeficientii ai, bi, i = 0,1,2,.,n-1 (n se presupune dat), modelul matematic este complet definit, intrucat structura modelului este intr-o forma standard. De asemenea, functia de transfer este un model parametric, deoarece are o forma standard:
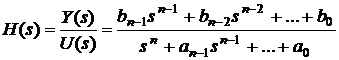 (2)
(2)
fiind complet definita de cei 2n parametri.
In descrierea structural - functionala, modelul matematic format din ecuatia de stare si de iesire este tot un model parametric. Intrucat ne referim la un sistem cu o intrare u(t) si o iesire y(t), cauzal, ecuatiile de stare si de iesire sunt:
![]() ; (ecuatia
de stare) (3)
; (ecuatia
de stare) (3)
![]() (ecuatia
de iesire) (4)
(ecuatia
de iesire) (4)
(A se observa lipsa termenului Du ca urmare a faptului ca sistemul este "cauzal", adica efectul apare in urma cauzei si nu odata cu aceasta, sau inaintea acesteia).
MODELE NEPARAMETRICE
Modele neparametrice in domeniul "t"
Fie un sistem SISO. Modelul parametric general de tip intrare-iesire al sistemului sau elementului considerat poate fi ecuatia diferentiala:
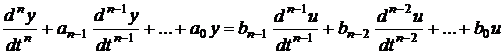 (5)
(5)
sau functia de
transfer: 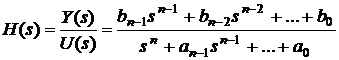 (6)
(6)
Din relatia de definitie a functiei de transfer, rezulta: Y(s) = H(s) U(s) (7)
Daca se aplica la intrarea sistemului, un semnal u(t), variatia marimii de iesire, y(t), se numeste raspunsul sistemului la semnalul de intrare aplicat. Atunci cand toate conditiile initiale sunt nule, raspunsul sistemului, y(t), se numeste normal.
Consideram ca la intrarea sistemului se aplica, in conditii initiale nule, un impuls unitar:
u(t) = δ(t) (8)
Transformata Laplace a marimii de intrare este, in acest caz,
U(s) = L[δ(t)] = 1 (9)
Imaginea Laplace a raspunsului normal al sistemului se deduce din relatia (7), punand U(s) = 1:
Y(s) = H(s) (10)
Raspunsul normal al sistemului sau elementului considerat, la un impuls unitar, este transformata Laplace inversa a functiei de transfer si se numeste functie pondere, fiind notata cu
h(t): h(t) ≡ y(t) = L-1[H(s)] (11)
Rezulta ca functia de transfer poate fi definita ca transformata Laplace directa a functiei pondere. Prin urmare, functia pondere, cat si functia de transfer, reprezinta forme de reprezentare a modelului matematic al sistemului sau elementului respectiv, legate prin corespondenta biunivoca,
L
![]()
![]() h(t) H(s) (12)
h(t) H(s) (12)
L-1
Functia pondere este, insa, o caracteristica ce se poate stabili pe cale experimentala.
Daca la intrarea sistemului se aplica un impuls unitar real, u(t) = δ*(t,ε) si inregistram - cu un aparat de masura inregistrator - curba de variatie a marimii de iesire (figura 1), se obtine o reprezentare neparametrica a modelului, sub forma curbei y(t) ≈ h(t) inregistrate.
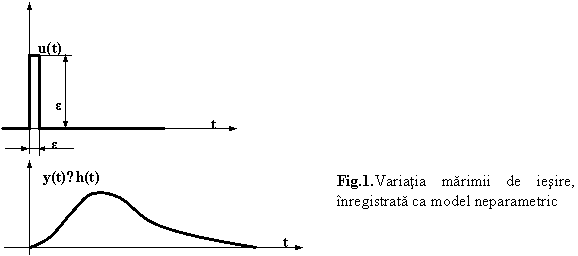
Procedura prezentata constituie o cale simpla de obtinere a modelului matematic al unui sistem - in reprezentare neparametrica - utilizabila atunci cand dispunem de sistemul fizic, pentru realizarea experimentului.
Sa consideram in continuare, ca se aplica la intrare un semnal u(t) oarecare. Imaginea Laplace a raspunsului normal al sistemului este data de relatia (7), de unde rezulta:
y(t) = L-1[H(s)U(s)] (13)
Utilizand teorema inmultirii imaginilor din transformata Laplace, se obtine:
y(t)
= 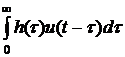 (14)
(14)
Aceasta ecuatie reprezinta ecuatia intrare-iesire a sistemului, in care descrierea matematica se realizeaza prin intermediul functiei pondere.
Utilizarea in ecuatia (14) a functiei h(t), data sub forma inregistrarii grafice experimentale, este dificila si de aceea se recurge la o aproximare a reprezentarii neparametrice, astfel incat aceasta sa fie definita prin intermediul unui numar finit de parametri.
In figura 2 este ilustrata o posibilitate de caracterizare a functiei pondere h(t) printr-un numar finit de parametri (operatie numita parametrizare).

T 2T..kT N
Parametrii adoptati sunt valorile functiei pondere la momentele discrete kT, k = 0, 1, .,N.
Se
considera, in cazul sistemelor pentru care este indeplinita
conditia ![]() , (adica sisteme care se numesc "cu memorie
finita", deoarece functia pondere revine dupa un anumit timp
practic finit, la valoarea initiala) ca pentru t > NT,
h(t)≈0.
, (adica sisteme care se numesc "cu memorie
finita", deoarece functia pondere revine dupa un anumit timp
practic finit, la valoarea initiala) ca pentru t > NT,
h(t)≈0.
Pasul de discretizare a timpului, T, se adopta din doua cerinte contradictorii: descrierea suficient de precisa a inregistrarii grafice h(t) si considerarea unui numar cat mai mic de parametri ai modelului.
Evaluarea numerica, prin metoda dreptunghiurilor, a integralei de convolutie (14), cu utilizarea pasului de integrare egal cu T, conduce la transformarea ecuatiei intrare-iesire, sub forma:
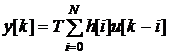 ; (
; (![]()
![]() ) (15)
) (15)
Aceasta ecuatie constituie cea mai simpla expresie a unei reprezentari matematice de tip intrare-iesire, care are la baza modelul neparametric h(t), (adica inregistrarea experimentala a functiei pondere).
Dupa cum se stie, semnalul de proba cel mai utilizat in practica este semnalul treapta. Daca la intrarea sistemului se aplica o variatie in treapta unitara,
![]() (16)
(16)
![]() (17)
(17)
Raspunsul
normal al sistemului la o treapta unitara aplicata la intrare se
numeste functie indiciala si se noteaza
prin ![]() . In conformitate cu relatia (17) si cu teorema
integrarii din transformata Laplace, se obtine:
. In conformitate cu relatia (17) si cu teorema
integrarii din transformata Laplace, se obtine:
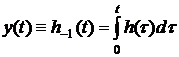 (18)
(18)
adica functia indiciala este integrala functiei pondere.
Avand in vedere ca pentru conditii initiale nule, corespondenta
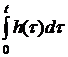
![]()
![]() h(t)
h(t) ![]() (19)
(19)
![]()
este biunivoca, rezulta ca si functia indiciala - dedusa cu usurinta pe cale experimentala sub forma unei inregistrari grafice - reprezinta un model neparametric.
Reprezentarile neparametrice in domeniul "t" pot fi utilizate ca atare pentru analiza si sinteza sistemelor (evident, sub forma unor parametrizari de tipul celei ilustrate in figura 2, sau constituie forme primare de reprezentare matematica a modelelor (obtinute pe cale experimentala), din care se deduc - prin metode de conversie - alte modele parametrice necesare in analiza si proiectarea sistemelor.
|
Politica de confidentialitate |
| Copyright ©
2024 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |