
Metode integrale pentru analiza Fourier
Teoria fenomenologica a largirii liniei de difractie in cazul metalelor si aliajelor deformate plastic a fost dezvoltata acum aproape 50 de ani (Warren si Averbach 1950; Warren 1959). Aceasta teorie identifica doua tipuri de contributii la largirea liniei de difractie: una datorata dimensiunii de cristalit si una datorata deformarii. Primul tip de largire depinde de dimensiunea domeniilor de imprastiere coerenta, iar largirea datorata deformarii este cauzata de orice imperfectiune a retelei (dislocatii si diferite defecte punctiforme).
Dezvoltarea acestui camp al cercetarii a inceput atunci cand Sherrer (1918) a inteles ca dimensiunile mici de cristalitele conduc la largirea liniilor de difractie. Totusi, a trebuit sa treaca mai mult de un sfert de secol pana cand o teorie mai complexa si mult mai exacta sa fie formulata de Stokes si Wilson (1944). Ei au fost primii care au considerat deformarea retelei cristaline ca o alta sursa a largirii liniei de difractie. La putin timp teoria lor a fost imbunatatita semnificativ: Stokes (1948) a adaptat metoda deconvolutiei Fourier pentru a extrage din spectrul observat profilul fizic al liniei de difractie.
Rezultatele obtinute de Bertaut (1949) si Warren si Averbach (1950; 1952) au facut posibila o analiza mult mai detaliata a formei profilului liniei de difractie. In 1962, Wilson a introdus analiza variantei profilului, iar Ergun (1968) metoda convolutiilor succesive.
Desi metoda lui Stokes a impus limitari severe analizei, metoda Warren-Averbach de separare a largirii dimensiune-deformare a ramas cea mai putin restrictiva metoda pentru analiza largirii liniei de difractie.
Metode
Profilul observat al liniei de difractie este o convolutie a profilului instrumental g(x) cu profilul fizic f(x) (profilul probei), plus fond (Taupin 1973):
![]() (1)
(1)
Distributia dupa lungimea de unda ω(x) si aberatiile geometrice γ(x) sunt tratate de obicei ca fiind caracteristice unui anumit instrument (profilul instrumental):
![]() (2)
(2)
Pentru a obtine parametrii microstructurali ai probei analizate, trebuie ca profilul fizic (contributia probei) sa fie extras din profilul observat, h.
Sursele pentru contributia probei la largirea liniei de difractie sunt numeroase: dimensiunea de cristalit, imperfectiuni ale retelei cristaline (dislocatii, vacante, atomi interstitiali si substitutionali) care duc la deformarea acesteia, si defecte extinse (retele de dislocatii, stacking faults, twins, large angle boundaries, etc)
Extragerea profilului fizic din profilul observat necesita o determinare prealabila a profilului instrumental. In acest scop se poate folosi un material standard (ex LaB6) sau un material etalon propriu care sa indeplineasca anumite caracteristici: dimensiunea de cristalit cuprinsa intre 1-5 microni, lipsa defectelor structurale si puritate ridicata (ex: ZnO recristalizat la 1000 grade Celsius utilizat in aceasta lucrare la caracterizarea pulberilor de ZnO).
Daca se foloseste un standard ca LaB6, ale carei linii de difractie nu coincid cu cele ale probei analizate, este necesara modelarea analitica a parametrilor caracteristici a formei profilurilor liniilor de difractie, astfel incat profilul instrumental sa fie determinat pentru orice unghi de interes. In acest scop se foloseste relatia (Caglioti et all 1958):
![]() (3)
(3)
Este foarte important ca functia instrumentala sa descrie in mod corect variatia caracteristica unghiulara a parametrilor instrumentali. Asimetria este modelata de cele mai multe ori de o functie Peareson-VII (Hall et all. 1977), in care variatia unghiulara a parametrului m care descrie forma functiei Pearson-VII poate fi definit ca (Howard si Snyder 1989):
![]() (4)
(4)
Metodele de extragere a profilului fizic pot fi impartite in doua mari grupe:
- metode care presupun o deconvolutie, in care profilul fizic este extras din profilul observat folosind profilul instrumental determinat in prealabil (cea mai folosita este metoda transformatelor Fourier - Stokes 1948);
- metode care presupun o convolutie, in care profilul observat este construit si ajustat la cel obtinut experimental printr-o fitare cu functii analitice prin metoda celor mai mici patrate.
Metode integrale
1.1.1 Metoda lui Sherrer
Formula lui Scherrer stabileste ca
largimea integrala a liniei de difractie in spatiul
reciproc ![]() este invers
proportionala cu dimensiunea aparenta
este invers
proportionala cu dimensiunea aparenta ![]() :
: ![]() . Formula a fost obtinuta in ipoteza ca singura
cauza fizica a largirii liniei de difractie este
dimensiunea cristalitelor.
. Formula a fost obtinuta in ipoteza ca singura
cauza fizica a largirii liniei de difractie este
dimensiunea cristalitelor. ![]() se numeste
constanta Scherrer si ia valori in intervalul
se numeste
constanta Scherrer si ia valori in intervalul ![]() .
.
Largimea
integrala a liniei de difractie in spatiul reciproc ![]() depinde de
largimea liniei de difractie in spatiul real
depinde de
largimea liniei de difractie in spatiul real ![]() prin relatia:
prin relatia: ![]() .
.
In
aceasta formula ![]() se exprima in
radiani. Largimea integrala a liniei de difractie in
spatiul reciproc
se exprima in
radiani. Largimea integrala a liniei de difractie in
spatiul reciproc ![]() se exprima in
se exprima in![]() , daca lungimea de unda a radiatiei X
incidente este exprimata in
, daca lungimea de unda a radiatiei X
incidente este exprimata in ![]()
Formula
lui Sherrer devine: ![]() , in care
, in care ![]() se exprima in
radiani, iar
se exprima in
radiani, iar ![]() se obtine in
se obtine in ![]() , daca lungimea de unda a radiatiei X
, daca lungimea de unda a radiatiei X ![]() se exprima in
se exprima in ![]() .
.
In
ipoteza ca domeniul cristalin este impartit in coloane de celule
elementare, orientate in lungul vectorului de difractie si a
caror lungime ![]() este variabila,
este variabila, ![]() .
. ![]() si
si ![]() reprezinta
momentele de ordinul 3, respectiv 4, corespunzatoare functiei de
distributie a lungimilor coloanelor (Langford&Wilson, 1978). In acest
caz,
reprezinta
momentele de ordinul 3, respectiv 4, corespunzatoare functiei de
distributie a lungimilor coloanelor (Langford&Wilson, 1978). In acest
caz, ![]() reprezinta lungimea
coloanelor mediata in volum. Aceasta interpretare este
acceptata in prezent de catre specialisti si ea este
raportata ca dimensiune a cristalitelor (Langford&Wilson, 1978;
Scardi&Leoni, 2001).
reprezinta lungimea
coloanelor mediata in volum. Aceasta interpretare este
acceptata in prezent de catre specialisti si ea este
raportata ca dimensiune a cristalitelor (Langford&Wilson, 1978;
Scardi&Leoni, 2001).
1.1.2 Metoda Williamson-Hall (WH method)
In aceasta metoda se presupune ca
largirea liniei de difractie se datoreaza dimensiunilor de
cristalite (caracterizate prin lungimea
coloanelor madiata in volum) si deformatiilor celulei elementare
(caracterizate prin deformatia relativa ![]() ). Largimea integrala datorata dimensiunilor
de cristalite se noteaza cu
). Largimea integrala datorata dimensiunilor
de cristalite se noteaza cu ![]() , iar largimea integrala datorata
deformatiilor celulei elementare se noteaza cu
, iar largimea integrala datorata
deformatiilor celulei elementare se noteaza cu ![]() .
.
Cele
mai folosite formule in aceasta metoda sunt (Langford, 1992): ![]()
![]() ,
,
in care ![]() este largimea
integrala totala in spatiul reciproc.
este largimea
integrala totala in spatiul reciproc.
Pentru
determinarea valorilor marimilor ![]() si
si ![]() se reprezinta
grafic dependentele
se reprezinta
grafic dependentele ![]() sau
sau ![]() . Graficele acestor dependente sunt o dreapta
descrisa de ecuatia
. Graficele acestor dependente sunt o dreapta
descrisa de ecuatia ![]() , respectiv o parabola descrisa de ecuatia
, respectiv o parabola descrisa de ecuatia ![]() . Prelucrarea acestor grafice prin metoda celor mai mici
patrate permite determinarea valorilor parametrilor
. Prelucrarea acestor grafice prin metoda celor mai mici
patrate permite determinarea valorilor parametrilor ![]()
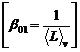 si
si ![]()
![]() pentru primul caz,
respectiv
pentru primul caz,
respectiv ![]()
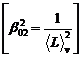 si
si ![]()
![]() pentru al doilea caz.
pentru al doilea caz.
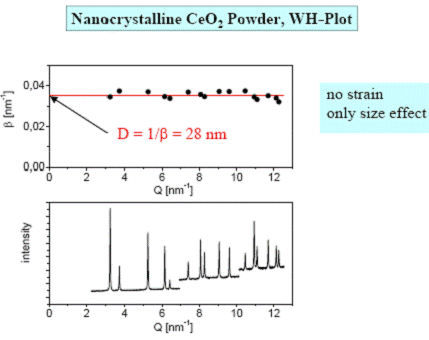
In
figura . se prezinta determinarea dimensiunii medii a cristalitelor
si a microtensiunilor cu ajutorul metodei Williamson-Hall. Analiza este
facuta pentru o pulbere nanocristalina din ![]() .
.
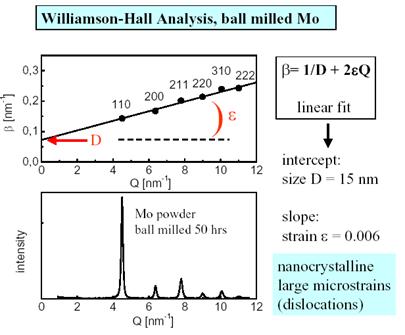
Determinarea dimensiunii medii a cristalitelor si a microtensiunilor poate fi facuta si analitic, daca se cunosc largimile integrale ale profilurilor fizice pentru doua linii de difractie de ordinul 1 si de ordinul 2, pentru acelasi sistem de plane cristaline. Cele doua marimi se determina cu ajutorul ecuatiilor (7), (8) sau (9):
![]() (7),
(7), ![]() 8),
8), ![]() (9)
(9)
In
aceste ecuatii: ![]() reprezinta
largimea integrala a liniei de difractie,
reprezinta
largimea integrala a liniei de difractie, ![]() reprezinta
dimensiunea de cristalite mediata in volum,
reprezinta
dimensiunea de cristalite mediata in volum, ![]() reprezinta limita
superioara a microtensiunilor,
reprezinta limita
superioara a microtensiunilor, ![]() .
.
Ecuatia (7) se aplica in ipoteza ca profilurile liniei de difractie datorate dimensiunilor cristalitelor si microtensiunilor sunt descrise de functii de distributie Cauchy (Cauchy-Cauchy). Ecuatia (8) se aplica in ipoteza ca profilele liniei de difractie datorate dimensiunilor cristalitelor si microtensiunilor sunt descrise de functiile de distributie Cauchy, respectiv Gauss (Cauchy-Gauss). Ecuatia (9) se aplica in ipoteza ca profilele liniei de difractie datorate dimensiunilor cristalitelor si microtensiunilor sunt descrise de functii de distributie Gauss (Gauss-Gauss).
Aplicand ecuatiile (7), (8) si (9) pentru ordinele de difractie 1 si 2 ale unei linii de difractie, se obtin formulele de calcul (10) si (11) pentru calculul dimensiunilor de cristalite si a microtensiunilor.
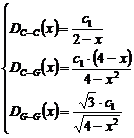 (10) ,
(10) , 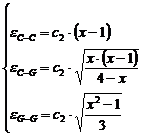 (11)
(11)
In
formulele (10) si (11): ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
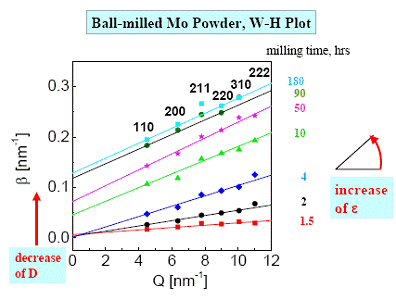
1.1.3. Metoda Williamson-Hall modificata (MWH method
Limitarea metodei Williamson-Hall consta in faptul ca efectele de anizotropie datorate deformarilor celulei elementare nu sunt luate in considerare. Largimea integrala a liniei de difractie se datoreaza si deformarilor datorate disclocatiilor intr-un mediu elastic ..
Metoda
Williamson-Hall modificata (MWH - Modified Williamson-Hall) ia in
considerare natura si dependenta de directiile cristalografice a
campurilor de deformatii datorate defectelor celulei elementare.
Dislocatiile constituie sursa principala a deformatiilor celulei
elementare ![]() (microdeformatiilor). Pentru descrierea dependentei
acestora de directia
(microdeformatiilor). Pentru descrierea dependentei
acestora de directia ![]() se foloseste
factorul de contrast. Valoarea medie a factorului de contrast
se foloseste
factorul de contrast. Valoarea medie a factorului de contrast ![]() a fost inclusa
(Wilkens, 1970; Ungar et al., 1999) in ecuatiile . si 2 WH astfel:
a fost inclusa
(Wilkens, 1970; Ungar et al., 1999) in ecuatiile . si 2 WH astfel:
![]()
![]() ,
,
unde ![]() este densitatea
dislocatiilor,
este densitatea
dislocatiilor, ![]() este o constanta
care depinde de vectorul Burgers
este o constanta
care depinde de vectorul Burgers ![]() si de raza de
taiere a dislocatiilor
si de raza de
taiere a dislocatiilor ![]() . Functia
. Functia ![]() contine termenii
superiori care depind de dislocatii (Ungar et al., 1998).
contine termenii
superiori care depind de dislocatii (Ungar et al., 1998).
Pentru
materialele cu simetrie cubica, factorul de contrast poate fi scris ca o
functie simpla de indicii ![]() (Stokes&Wilson,
1944; Kivoglaz et al., 1983):
(Stokes&Wilson,
1944; Kivoglaz et al., 1983):
![]() .
.
Valorile
coeficientilor ![]() si
si ![]() au fost calculate cu
ajutorul constantelor elastice (
au fost calculate cu
ajutorul constantelor elastice (![]() sau
sau ![]() ) pentru dislocatii elicoidale si de margine
(Wilkens, 1987; Armstrong, Kalceff et al., 2004).
) pentru dislocatii elicoidale si de margine
(Wilkens, 1987; Armstrong, Kalceff et al., 2004).
O
notatie alternativa a coeficientului de contrast se introduce cu
ajutorul relatiei ![]() , unde
, unde ![]() si
si ![]() (Ungar&Tichy,
1999; Ungar et al., 1999).
(Ungar&Tichy,
1999; Ungar et al., 1999).
Daca sunt prezente defectele planare, atunci expresiile MWH trebuie corectate prin introducerea unui termen aditional:
![]()
![]()
In ecuatiile de mai sus, ![]() este probabilitatea
globala a defectelor de retea, in care
este probabilitatea
globala a defectelor de retea, in care ![]() reprezinta
probabilitatea defectelor de impachetare,
reprezinta
probabilitatea defectelor de impachetare, ![]() reprezinta
probabilitatea defectelor de ingemanare si
reprezinta
probabilitatea defectelor de ingemanare si ![]() este constanta celulei
elementare.
este constanta celulei
elementare.
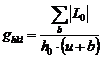 , unde
, unde ![]() ,
, ![]() , iar
, iar ![]() reprezinta
multiplicitatea familiei de plane
reprezinta
multiplicitatea familiei de plane ![]() .
.
1.1.4. Metoda Warren-Averbach
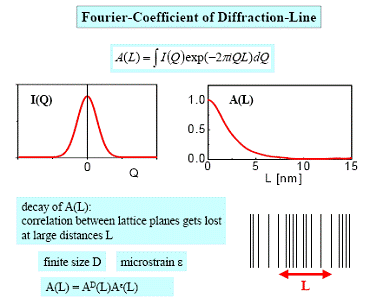
Aceasta metoda se bazeaza pe analiza Fourier a profilului liniei de difractie.
Convolutiei functiilor de profil ale dimensiunilor de cristalite si ale microdeformatiilor in spatiul reciproc ii corespunde produsul transformatelor Fourier in spatiul real.
Coeficientii
functiilor cosinus ai transformatei Fourier pentru profilul fizic
(structural) ![]() se calculeaza cu
formula:
se calculeaza cu
formula:
![]() ,
,
in care coeficientul transfoematei Fourier care depinde de dimensiunile de cristalite este independent de ordinul de difractie, iar coeficientul transformatei Fourier care depinde de microdeformatii este dependent de ordinul de difractie.
Coeficientul Fourier ![]() care determina
dimensiunea cristalitelor se calculeaza cu formula (Guinier, 1963):
care determina
dimensiunea cristalitelor se calculeaza cu formula (Guinier, 1963):
 ,
,
unde ![]()
Dimensiunea
medie a cristalitelor mediata in suprafata ![]() , functiile de distributie ale lungimilor
coloanelor celulelor elementare mediate in suprafata
, functiile de distributie ale lungimilor
coloanelor celulelor elementare mediate in suprafata ![]() , respectiv
in volum
, respectiv
in volum ![]() , se
calculeaza cu formulele:
, se
calculeaza cu formulele:
![]() si
si ![]()
In metoda
Waren-Averbach, deformatia relativa se defineste cu relatia ![]() , unde
, unde ![]() este lungimea nedeformata a coloanei de
celule elementare, iar
este lungimea nedeformata a coloanei de
celule elementare, iar ![]() este deformatia
coloanei respective.
este deformatia
coloanei respective.
Coeficientii Fourier care depind de deformatii se calculeaza cu relatia:
Pentru valori mici ale lui ![]() aproximatia
folosita pentru calculul mediu al exponentei este data de
relatia:
aproximatia
folosita pentru calculul mediu al exponentei este data de
relatia:
![]() .
.
Aceasta
relatie este exacta, daca deformatiile relative ![]() ...
...
Daca
se cunosc profilele experimentale pentru doua ordine de difractie pe
aceeasi famile de plane cristaline, atunci se pot determina
coeficientii Fourier ![]() si
si ![]() .
.
Metoda Warren-Averbach presupune ca microdeformatiile sunt
mici si sunt distribuite dupa o functie Gauss ![]() pentru toate valorile
parametrului
pentru toate valorile
parametrului ![]() . In acest caz, separarea celor doua efecte se
realizeaza cu ajutorul formulei:
. In acest caz, separarea celor doua efecte se
realizeaza cu ajutorul formulei:
![]() .
.
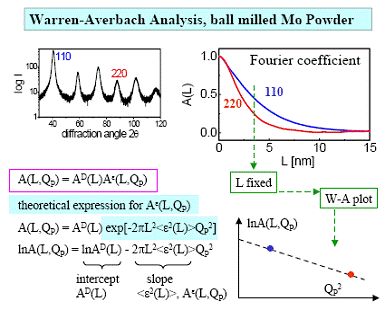
In aproximatia data, se obtine:
![]() ,
,
in care ![]() reprezinta
deformatia relativa patratica medie corelata cu
distanta
reprezinta
deformatia relativa patratica medie corelata cu
distanta ![]() . Pentru a obtine graficul dreptei
. Pentru a obtine graficul dreptei ![]() , pentru
, pentru ![]() dat, se
reprezinta punctele
dat, se
reprezinta punctele ![]() pentru reflexiile
Bragg de ordinul 1 si 2 pe acelasi sistem de plane cristaline.
Prelucrarea dreptei obtinute prin metoda celor mai mici patrate,
permite determinarea valorilor lui
pentru reflexiile
Bragg de ordinul 1 si 2 pe acelasi sistem de plane cristaline.
Prelucrarea dreptei obtinute prin metoda celor mai mici patrate,
permite determinarea valorilor lui ![]() si a lui
si a lui ![]() - vezi figura
- vezi figura
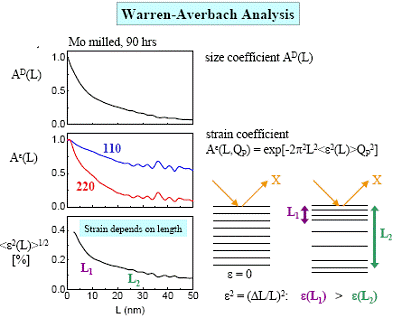
Daca profilul liniei de difractie, datorat dimensiunilor de cristalie, este descris de o functie Voigt, atunci coeficientii transformatei Fourier a functiei Voigt se calculeaza cu relatia:
![]()
Derivand relatia (.), se obtine:
![]()
Daca functiile de distributie ale lungimilor coloanelor sunt cunoscute, atunci se pot evalua dimensiunile medii ale cristalitelor mediate in suprafata sau volum cu formulele:
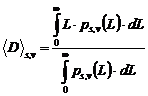 .
.
Integralele de acest tip pot fi calculate analitic (Prudnikov si altii, 1986):
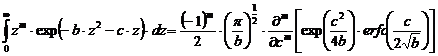 Pentru
dimensiunile de cristalie mediate in suprafata si in volum se
obtin formulele de calcul:
Pentru
dimensiunile de cristalie mediate in suprafata si in volum se
obtin formulele de calcul:
![]() si
si
![]()
Daca profilul liniei de difractie, datorat microdeformatiilor, este descris de o functie Voigt, atunci coeficientii transformatei Fourier a functiei Voigt se calculeaza cu formula:
![]() ,
,
iar deformatiile relative patratice medii se calculeaza cu formula:
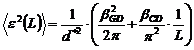 .
.
Se
observa ca deformatiile relative patratice medii scad cu
cresterea lui ![]() . Formula de calcul a deformatiilor relative
patratice medii contine un termen independent de
. Formula de calcul a deformatiilor relative
patratice medii contine un termen independent de ![]() si unul de
pendent de
si unul de
pendent de ![]() :
:
![]() , in care
, in care ![]() si
si
![]() , in care
, in care ![]()
Profilul liniei de difractie al probei
masurate este descris de functia ![]() care reprezinta
convolutia functiilor care descriu profilul fizic
care reprezinta
convolutia functiilor care descriu profilul fizic ![]() si profilul
instrumental
si profilul
instrumental![]() :
:
![]() . (3)
. (3)
In
ecuatia (3), ![]() .
.
Transformata
Fourier a functiei ![]() este egala cu
produsul transformatelor Fourier ale functiilor care descriu profilele
fizic, respectiv instrumental:
este egala cu
produsul transformatelor Fourier ale functiilor care descriu profilele
fizic, respectiv instrumental: ![]() . (4)
. (4)
Metoda
Warren-Averbach se bazeaza pe determinarea transformatelor Fourier ![]() si
si ![]() din analiza profilelor
liniilor de difractie masurate pentru proba standard
din analiza profilelor
liniilor de difractie masurate pentru proba standard ![]() si pentru proba
analizata. Astfel se poate determina inversa transformatei Fourier a
functiei
si pentru proba
analizata. Astfel se poate determina inversa transformatei Fourier a
functiei ![]() si calcula
si calcula ![]() . Rezultatul poate fi scris sub forma unei serii Fourier:
. Rezultatul poate fi scris sub forma unei serii Fourier:
![]() ,
,
unde ![]() si
si ![]() sunt coeficientii
functiilor cosinus si sinus, iar
sunt coeficientii
functiilor cosinus si sinus, iar ![]() este lungimea coloanei
formate din celule elementare si care este perpendiculara pe planele
de difractie corespunzatoare liniei analizate.
este lungimea coloanei
formate din celule elementare si care este perpendiculara pe planele
de difractie corespunzatoare liniei analizate.
Coeficientii
![]() sunt folositi
pentru a determina dimensiunea mediata in plan a cristalitelor
sunt folositi
pentru a determina dimensiunea mediata in plan a cristalitelor ![]() si
microtensiunile celulei elementare. Daca se folosesc doua linii de
difractie, corespunzatoare Se observa ca
deformatiile relative patratice medii scad cu cresterea lui
si
microtensiunile celulei elementare. Daca se folosesc doua linii de
difractie, corespunzatoare Se observa ca
deformatiile relative patratice medii scad cu cresterea lui ![]() . Formula de calcul a deformatiilor relative
patratice medii contine un termen independent de
. Formula de calcul a deformatiilor relative
patratice medii contine un termen independent de ![]() si unul de
pendent de
si unul de
pendent de ![]() :
:
![]() , in care
, in care ![]() si
si
![]() , in care
, in care ![]()
Profilul liniei de difractie al probei
masurate este descris de functia ![]() care reprezinta
convolutia functiilor care descriu profilul fizic
care reprezinta
convolutia functiilor care descriu profilul fizic ![]() si profilul
instrumental
si profilul
instrumental![]() :
:
![]() . (3)
. (3)
In
ecuatia (3), ![]() .
.
![]() Transformata Fourier a functiei
Transformata Fourier a functiei ![]() este egala cu
produsul transformatelor Fourier ale functiilor care descriu profilele
fizic, respectiv instrumental:
este egala cu
produsul transformatelor Fourier ale functiilor care descriu profilele
fizic, respectiv instrumental: ![]() . (4)
. (4)
Metoda
Warren-Averbach se bazeaza pe determinarea transformatelor Fourier ![]() si
si ![]() din analiza profilelor
liniilor de difractie masurate pentru proba standard
din analiza profilelor
liniilor de difractie masurate pentru proba standard ![]() si pentru proba
analizata. Astfel se poate determina inversa transformatei Fourier a
functiei
si pentru proba
analizata. Astfel se poate determina inversa transformatei Fourier a
functiei ![]() si calcula
si calcula ![]() . Rezultatul poate fi scris sub forma unei serii Fourier:
. Rezultatul poate fi scris sub forma unei serii Fourier:
![]() ,
,
unde ![]() si
si ![]() sunt coeficientii
functiilor cosinus si sinus, iar
sunt coeficientii
functiilor cosinus si sinus, iar ![]() este lungimea coloanei
formate din celule elementare si care este perpendiculara pe planele
de difractie corespunzatoare liniei analizate.
este lungimea coloanei
formate din celule elementare si care este perpendiculara pe planele
de difractie corespunzatoare liniei analizate.
Coeficientii
![]() sunt folositi
pentru a determina dimensiunea mediata in plan a cristalitelor
sunt folositi
pentru a determina dimensiunea mediata in plan a cristalitelor ![]() si
microtensiunile celulei elementare. Daca se folosesc doua linii de
difractie, corespunzatoare ordinelor de difractie 1 si 2,
atunci se pot determina valorile celor doi parametrii.
si
microtensiunile celulei elementare. Daca se folosesc doua linii de
difractie, corespunzatoare ordinelor de difractie 1 si 2,
atunci se pot determina valorile celor doi parametrii.
Pentru a evalua dispersia dimensiunilor cristalitelor, trebuie introduse functiile de distributie ale dimensiunilor de cristalite. In prezent, cele mai folosite functii de distributie sunt:
functia
de distributie lognormala ![]() ;
;
functia
de distributie gamma ![]() ;
;
functia
de distributie propusa de York pentru fenomene de crestere normala ![]() .
.
Expresiile matematice ale acestor functii de distributie, precum si formulele de calcul pentru momentele de ordin n, sunt:
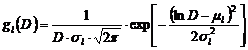 ,
, ![]()
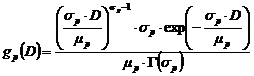 ,
, 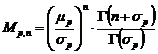
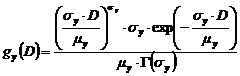 ,
, 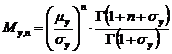
In relatiile (10), (11) si (12) :
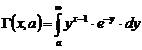 , iar
, iar ![]() ;
;
![]() este
este
![]() este momentul de ordin 2.
este momentul de ordin 2.
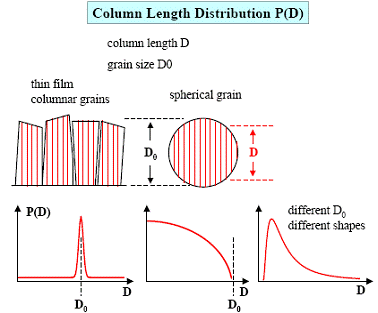
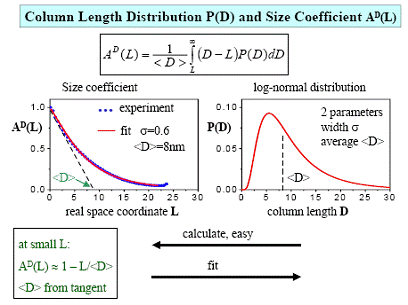
Metoda Warren-Averbach a avut un mare succes si este inca o metoda de
referinta in analiza profilului liniei de difractie. In afara
limitelor pentru aproximarea expansiunii, oricum, teoria Warren-Averbach nu
descrie mai degraba decat proprietatile fizice de baza ale
sistemelor cristaline: fiind legate de comportarea elastica a mediului
cristalin, distorsiunile de retea pot produce efecte anizotropice, iar
largimea liniei nu creste monoton cu ![]() .
.
Concluzii
Cele mai importane avantaje care rezulta din sinteza si fitarea liniilor si spectrelor de difractie cu radiatii X prin metoda convolutiei sunt:
Profilul liniei de difractie si dependenta unghiulara a acesteia pot fi descrise folosind un numar minim de parametrii si date. Acest lucru este posibil, deoarece in procedura de rafinament sunt folosite convolutia numerica si diferentierea numerica. In acest fel, in ecuatia convolutiei poate fi utilizata o gama variata de functii.
Numarul de parametri necesari pentru a descrie modelul este mai mic decat in "modelul functiei analitice" si corelarile dintre parametrii sunt reduse semnificativ.
Cresterea complexitatii profilului liniei de difractie nu conduce automat la cresterea numarului de parametrii necesari pentru descrierea lui.
Calitatea fitarii prin metoda convolutiei este mai buna decat in celelalte metode.
Folosirea modelelor fizice pentru descrierea profilului instrumental al difractometrelor in locul functiilor empirice selectate direct, conduce la modelul parametrilor fundamentali.
Metodele
lui Scherrer si Warren-Averbach permit determinarea a doi parametrii
diferiti, care caracterizeaza coloana de lungime ![]() , formata din celule elementare.
, formata din celule elementare.
Metoda
lui Scherrer permite determinarea marimii medii ![]() , iar metoda Warren-Averbach permite determinarea
marimii medii
, iar metoda Warren-Averbach permite determinarea
marimii medii ![]() .
.
Pentru determinarea dimensiunii medii a cristalitelor, trebuie sa se emita o ipoteza referitoare la forma acestora.
In ipoteza ca forma cristalitelor este sferica, formulele (5) si (6) permit calculul diametrului mediu al sferei:
![]() - metoda Sherrer (5)
- metoda Sherrer (5)
![]() - metoda
Warren-Averbach (6)
- metoda
Warren-Averbach (6)
Distributia dimensiunilor cristalitelor tinde spre o functie log-normala. In aceasta distributie exista un numar relativ mare de cristalite mici. Daca distributia log-normala este descrisa de functia:
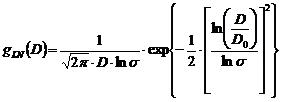 , (7)
, (7)
unde ![]() este valoarea
mediana si
este valoarea
mediana si ![]() este largimea
acestei distributii, atunci diferitele valori medii ale dimensiunilor
cristalitelor se calculeaza cu formulele:
este largimea
acestei distributii, atunci diferitele valori medii ale dimensiunilor
cristalitelor se calculeaza cu formulele:
![]() (8)
(8)
![]() (9)
(9)
![]() (10)
(10)
1.1.5. Metoda Warren Averbach modificata
In cazul in care deformarea este cauzata de dislocatii, Wilkens a calculat deformatia medie patratica, presupunand ca dislocatiile sunt distribuite la intamplare in mod restrictiv (restricted randomly distributed):
![]() (20)
(20)
unde b este lungimea vectorului
Burgers, ρ este densitatea de dislocatii, Re este raza
efectiva(outer cut-off radius) si C
este factorul de contrast al dislocatiei. Factorul de contrast depinde de
orientarea relativa a liniei, a vectorului Burgers si a vectorului de
difractie, ca si de constantele elastice ale materialului. Din cauza
distributiei reale de dislocatii din proba este necesara
medierea factorilor C ai dislocatiilor marginale si elicoidale cu sisteme de
alunecare diferite si orientarea sistemului de alunecare in
concordanta cu vectorul de difractie. Ungar si Tichy (1999)
au aratat ca pentru cristalele cubice si hexagonale, daca
distributia vectorilor Burgers este complet intamplatoare,
dependenta lui ![]() de hkl poate fi calculata in mod
explicit. Pentru cristalele cubice:
de hkl poate fi calculata in mod
explicit. Pentru cristalele cubice:
![]() , (21)
, (21)
unde ![]() h00 este
factorul mediu de contrast pentru reflexia h00,
q este o constanta care depinde
de constantele elastice ale cristalului si de tipul dislocatiei,
si H2=(h2k2+h2l2+k2l2)/(h2+k2+l2)2.
Atat
h00 este
factorul mediu de contrast pentru reflexia h00,
q este o constanta care depinde
de constantele elastice ale cristalului si de tipul dislocatiei,
si H2=(h2k2+h2l2+k2l2)/(h2+k2+l2)2.
Atat ![]() h00 cat si q au fost calculate
numeric pentru un numar de cazuri (Ungar et all 1999). In cazul cristalului hexagonal factorul mediu de
contrast al unui sistem de subalunecare este dat de ecuatia (Ungar,
Dragomir 2002):
h00 cat si q au fost calculate
numeric pentru un numar de cazuri (Ungar et all 1999). In cazul cristalului hexagonal factorul mediu de
contrast al unui sistem de subalunecare este dat de ecuatia (Ungar,
Dragomir 2002):
![]() (22)
(22)
aici x=(2/3)(l/(ga))2, unde a
este parametrul retelei in
stratul compact. ![]() hk,0, q1
si q2 au semnificatii analoge cazului cubic.
hk,0, q1
si q2 au semnificatii analoge cazului cubic.
Prin introducerea ecuatiei (20) in ecuatia (13) si logaritmand, ecuatia (12) devine ecuatia Warren-Averbach modificata:
(23)
Este clar din ecuatia (23) ca daca deformarea este produsa
de dislocatii, lnAL
trebuie reprezentat in functie de g2![]() in loc de g2. Aceasta este metoda Warren-Averbach
modificata. Trebuie mentionat ca efectele stivei de defecte si de
ingemanare trebuie luate in considerare in cazul acestei analize (Warren 2000).
Aplicarea cu succes a acestei operatii a fost facuta de Ungar et
al. (1998) prin includerea unui termen β'W(g)
in ecuatia Warren-Averbach, adica prin adaugarea unui parametru
in plus metodei.
in loc de g2. Aceasta este metoda Warren-Averbach
modificata. Trebuie mentionat ca efectele stivei de defecte si de
ingemanare trebuie luate in considerare in cazul acestei analize (Warren 2000).
Aplicarea cu succes a acestei operatii a fost facuta de Ungar et
al. (1998) prin includerea unui termen β'W(g)
in ecuatia Warren-Averbach, adica prin adaugarea unui parametru
in plus metodei.
Functia analitica folosita pentru descrierea profilului
Functia Gauss (G)
Expresia matematica a acestei functii este de forma:
![]() sau
sau 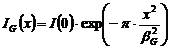
Daca
functia Gauss este normata la unitate ![]() , atunci expresia matematica a acesteia devine:
, atunci expresia matematica a acesteia devine:
![]() , unde
, unde 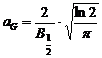 ,
, 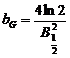
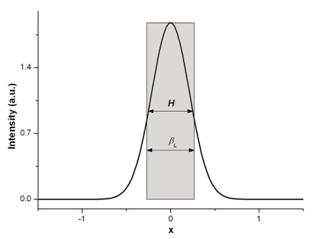
Largimea integrala a functiei Gauss este egala cu:
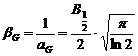 .
.
Factorul
de forma al functiei Gauss este egal cu ![]() .
.
In
figura 6 este prezentat graficul functiei Gauss, descrisa de
ecuatia cu doi parametrii: 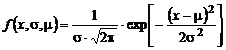 , pentru mai multe valori ale parametrului
, pentru mai multe valori ale parametrului ![]() care este proportional
cu largimea profilului graficului functiei la jumatatea
inaltimii maxime
care este proportional
cu largimea profilului graficului functiei la jumatatea
inaltimii maxime ![]() .
.
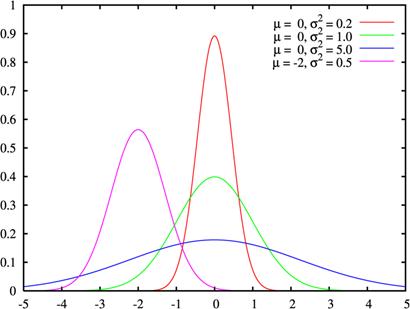 Figura 6. Graficul functiei Gauss
pentru diferite valori ale parametrilor
Figura 6. Graficul functiei Gauss
pentru diferite valori ale parametrilor
Functia Cauchy (C) sau Lorentz (L)
Expresia matematica a acestei functii este de forma:
![]() sau
sau 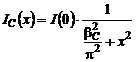
Daca
functia Lorentz este normata la unitate ![]() , atunci expresia matematica a acesteia devine:
, atunci expresia matematica a acesteia devine:
![]() , unde
, unde 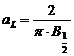 ,
, 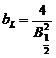 .
.
Largimea integrala a functiei Lorentz este egala cu:
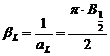
Factorul
de forma al functiei Lorentz este egal cu ![]() .
.
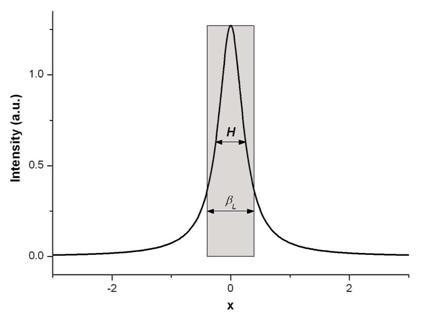
In
figura 7 este prezentat graficul functiei Cauchz (Lorentz), descrisa
de ecuatia ![]() pentru mai multe
valori ale parametrului
pentru mai multe
valori ale parametrului ![]() , care este proportional cu largimea profilului
graficului functiei la jumatatea inaltimii maxime
, care este proportional cu largimea profilului
graficului functiei la jumatatea inaltimii maxime ![]() .
.
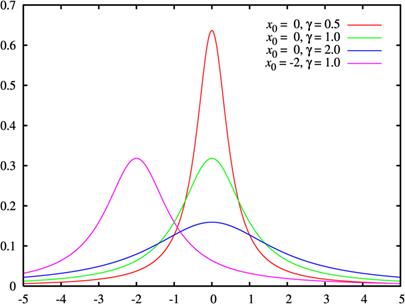
Figura 7. Graficul functiei Cauchy-Lorentz pentru diferite valori ale parametrilor
Nota. In ipoteza ca profilul liniei de
difractie masurate pentru o proba ![]() reprezinta
convolutia profilelor instrumental
reprezinta
convolutia profilelor instrumental ![]() si fizic
si fizic ![]() (Taupin, 1973):
(Taupin, 1973): ![]() , largimea integrala a profilului liniei de
difractie
, largimea integrala a profilului liniei de
difractie ![]() se poate calcula cu
formulele:
se poate calcula cu
formulele:
![]() (9), daca toate
profilele au forma descrisa de functia Cuachy;
(9), daca toate
profilele au forma descrisa de functia Cuachy;
![]() (10), daca toate
profilele au forma descrisa de functia Gauss.
(10), daca toate
profilele au forma descrisa de functia Gauss.
Functia Lorentz modificata
Expresia matematica a acestei functii normate la unitate este de forma:
![]() , unde
, unde 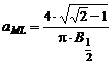 si
si 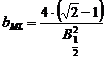
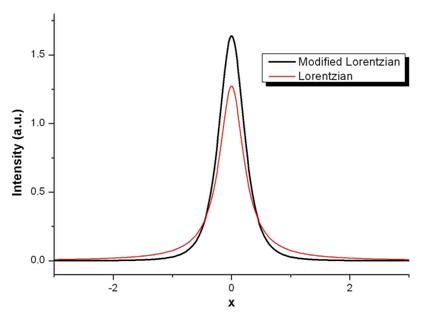
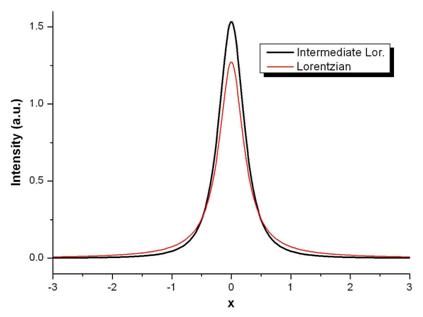
Functia Lorentz intermediara
Expresia matematica a acestei functii normate la unitate este de forma:
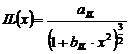 ,unde
,unde 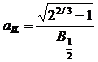 si
si 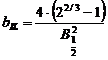 .
.
In majoritatea cazurilor liniile de difractie masurate sunt descrise bine cu ajutorul functiilor Cauchy sau Gauss (Klug si Alexander, 1974; Zoung si Wiles, 1982). In unele cazuri, pentru descrierea profilului liniilor de difractie cu radiatii X sau cu neutroni, trebuie sa se foloseasca functiile Voigt sau pseudo-Voigt (Wertheim si altii, 1974) sau functia Pearson-VII (Hall si altii, 1977).
Functia Pearson VII
Expresia matematica a acestei functii normate la unitate este de forma:
![]() ,
,
unde 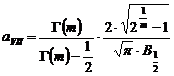 si
si 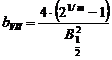
Functia pseudo-Voigt
Reprezinta o combinatie liniara
a unei functii Lorentz ![]() cu o functie
Gauss
cu o functie
Gauss ![]() , avand aceeasi largime la jumatatea
inaltimii maxime
, avand aceeasi largime la jumatatea
inaltimii maxime ![]() si se
defineste cu expresia matematica:
si se
defineste cu expresia matematica:
![]() ,
, ![]()
Functia
depinde de doi parametrii care caracterizeaza profilul liniei de
difractie: 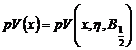 .
.
Largimea
integrala a functiei ![]() , normata la unitate, este egala cu inversul
valorii maxime a acestei functii:
, normata la unitate, este egala cu inversul
valorii maxime a acestei functii: ![]() .
.
Daca
functia ![]() este multiplicata
cu o constanta (intensitatea integrala), atunci largimea
integrala se calculeaza cu formula:
este multiplicata
cu o constanta (intensitatea integrala), atunci largimea
integrala se calculeaza cu formula:
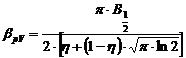
Functia
pseudo-Voigt ![]() inlocuieste
perechea de parametrii
inlocuieste
perechea de parametrii ![]() , care caracterizeaza functiile Lorentz si
Gauss, cu perechea de parametrii
, care caracterizeaza functiile Lorentz si
Gauss, cu perechea de parametrii ![]() , care caracterizeaza functia pseudo-Voigt.
, care caracterizeaza functia pseudo-Voigt.
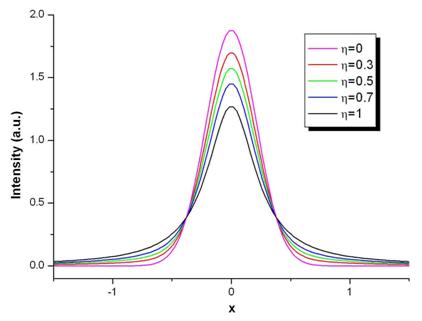
In programul FulProff expresia matematica folosita pentru functia Pseudo-Voigt este de forma:
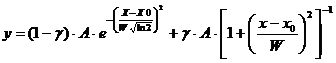
in care ![]()
![]()
![]() si
si ![]() sunt parametrii de fitare. In acest caz,
sunt parametrii de fitare. In acest caz, 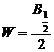 , iar
, iar ![]() reprezinta valoarea unghiului
reprezinta valoarea unghiului ![]() la care este centrata functia.
Parametrul
la care este centrata functia.
Parametrul ![]() reprezinta contributia
functiei Lorentz la functia pseudo-Voigt.
reprezinta contributia
functiei Lorentz la functia pseudo-Voigt.
Constrangerile impuse functiei pseudo-Voigt sunt urmatoarele:
Largimile
tuturor functiilor la semiinaltime ![]() au
aceeasi valoare.
au
aceeasi valoare.
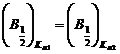 .
.
Contributiile
functiei Lorentz ![]() pentru radiatiile
pentru radiatiile
![]() si
si ![]() sunt egale.
sunt egale.
Functia Voigt (V)
Reprezinta convolutia unei functii Gauss cu o functie Lorentz:
![]() ,
,
in care functiile Lorentz si Gauss
au largimile la jumatatea inaltimii maxime ![]() egale:
egale: 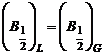 .
.
Expresia matematica a functiei Voigt folosita uzual (Langford, 1978) este:
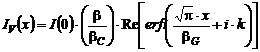 ,
,
unde ![]() . Functia complexa de eroare
. Functia complexa de eroare ![]() se defineste cu
formula
se defineste cu
formula ![]() , in care
, in care ![]() este conjugata
functiei complexe de eroare.
este conjugata
functiei complexe de eroare.
Largimea
integrala a functiei Voigt se calculeaza cu formula (Schoening,
1965: ![]() (9a)
(9a)
Halder si Wagner (1966) au propus o formula aproximativa de calcul care permite calculul rapid al largimii integrale:
![]() (10a).
(10a).
In cazul in care profilele sunt descrise de doua functii Voigt sau de o functie Voigt si o alta functie, largimea integrala se calculeaza cu formulele (9) si (10)
Functia
Voigt este o functie care depinde de largimea integrala a
functiei Lorentz ![]() si de
largimea integrala a functiei Gauss
si de
largimea integrala a functiei Gauss ![]() :
:
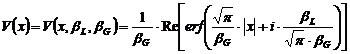 ,
,
unde ![]() .
.
In
figura 9 este prezentat graficul functiei Voigt, descrisa de
ecuatia ![]() , unde
, unde ![]() si
si ![]() pentru mai multe
valori ale parametrilor
pentru mai multe
valori ale parametrilor ![]() si
si ![]() .
.
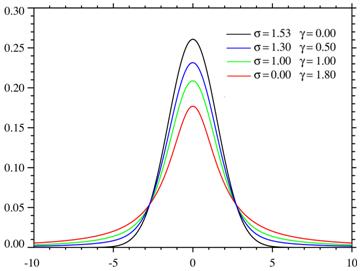
Figura 8. Graficul functiei Voigt pentru diferite
valori ale parametrilor ![]() si
si ![]() (Curba neagra corespunde graficului
functiei Gauss
(Curba neagra corespunde graficului
functiei Gauss ![]() , iar cea rosie - graficului functiei Lorentz
, iar cea rosie - graficului functiei Lorentz ![]()
|
Politica de confidentialitate |
| Copyright ©
2024 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |