
In anumite situatii, precum cel al uni numar mare de ecuatii, metodele iterative de rezolvare a ecuatiilor, precum metoda Gauss-Siedel, sunt mult mai avantajoase. Metodele de eliminare, precum cea Gaussiana sunt inclinate la erorile de rotunjire. Totodata, sub aspect fizic este posibila cunoasterea problemei, convergenta poate fi grabita, deoarece valorile initiale necesare metodelor iterative pot fi alese mult mai precis. Fie dat un set general de n ecuatii si implicit cu n necunoscute
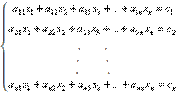
Daca elementele de pe diagonal sunt diferite de zero, atunci fiecare dintre ecuatii poate fi rescrisa in forma explicita pentru fiecare necunoscuta, respective prima ecuatie este rescrisa mentinand termenul x1 in partea stanga, iar a 2-a ecuatie cu termenul x2 pe partea stanga, s.a.m.d,

Sau rescrise in forma de suma:

De aici, in forma recursive dupa i,
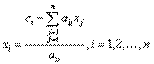
Pentru determinarea lui xi, in primul rand se presupune o valoare initiala pentru xi si apoi se utilizeaza forma rescrisa a ecuatiei pentru calculul noii valori. Reamintim, intotdeauna se utilizeaza valoarea calculate cel mai recent al lui xi. La sfarsitul fiecarei iteratii, in primul rand se calculeaza valoarea relative aproximativa, in valoare absoluta, pentru fiecare xi cu:
![]()
Atunci cand eroarea aproximativa relative in valoare absoluta este mai mica decat o tolerant predefinita, pentru fiecare dintre xi iteratiile vor fi stapate.
Viteza la lansare a unei rachete este specificata la 3 momente diferite de timp:
|
Timp, t s] |
Viteza, v m/s] |
Viteza este aproximata printr-un polinom ne ordinul2:
![]()
Coeficientii a1, a2, a3 pot fi determinate din:

Utilizand
metoda Gauss-Seidal. Se presupune urmatorul set de valori initiale de
start ![]() .
.
Rescriem ecuatiile date:

Iteratia #1:
Fiind dat vectorul solutiilor de start considerate initial, ca
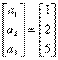
Obtinem:
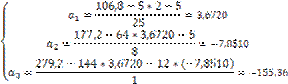
Eroarea relative aproximativa, in valoare absoluta, pentru fiecare xi este
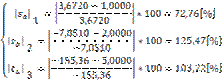
La
terminarea iteratiei vectorul cu solutiile initiale devine: 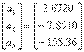 in
timp ce eroarea relative aproximativa, maxima, in valoare absoluta este
125.47%.
in
timp ce eroarea relative aproximativa, maxima, in valoare absoluta este
125.47%.
Iteratia #2:
In acest pas vectorul solutii initiale de start este cel rezultat la iteratia #1
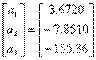
Iar ceea ce se obtine este:
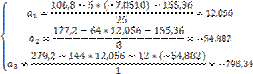
Eroarea relative aproximativa, in valoare absoluta, pentru fiecare xi este
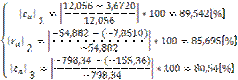
La
terminarea iteratiei vectorul cu solutiile initiale devine: 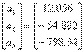 in timp ce eroarea relative aproximativa,
maxima, in valoare absoluta este 85.695%.Realizand un numar mai mare de
iteratii se obtin trmatoarele valori pentru vectorul solutii, precum si
valorile erorilor relative aproximative in valoare absoluta, corespunzatoare
acestor solutii.
in timp ce eroarea relative aproximativa,
maxima, in valoare absoluta este 85.695%.Realizand un numar mai mare de
iteratii se obtin trmatoarele valori pentru vectorul solutii, precum si
valorile erorilor relative aproximative in valoare absoluta, corespunzatoare
acestor solutii.
|
Iteration |
a1 |
|
a2 |
|
a3 |
|
Asa cum se vede din tabelul de mai sus Solutia nu converge catre valoarea exacta:
![]()
O capcana a metodelor iterative este aceia ca Solutia poate sa nu convearga, cu toate ca o anumita clasa de sisteme de ecuatii simultane converg la o solutie prin Gauss-Seidel. Pentru aceasta clasa de sisteme de ecuatii matricea coeficientilor [A] din [A][X] = [C] este dominant diagonal, respective:
|
Pentru orice i |
Cel putin pentru un i |
|
|
|
Daca un system de ecuatii are o matrice a coeficientilor care nu este dominant diagonal, ea poate sau nu sa convearga. Din fericire, cele mai multe sisteme fizice conduc spre sisteme de ecuatii lineare simultane, ce au matricea coeficientilor dominant diagonal, care asigura convergenta prin metode de iteratie, precum metoda Gauss-Seidel de rezolvare a ecuatiilor lineare simultane.
Fie dat sistemul de ecuatii:
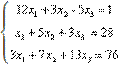
Care
utilizeaza metoda Gauss-Seidel pentru determinarea solutiilor. Se atribuie ca
valori initiale de start 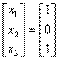
Matricea coeficientilor:
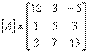
Este dominant diagonal, deoarece
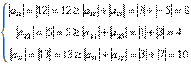
Inegalitatile sunt strict mai mari pentru cel putin un rand. Din acest motiv, Solutia trebuie sa convearga prin metoda Gauss-Seidel. Rescriind ecuatiile obtinem:

Presupunand vectorul solutiilor initiale de start
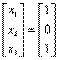
Iteratia #1:
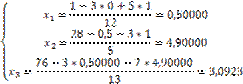
Eroarea relative aproximativa, in valori absolute, la terminarea primei iterati, este
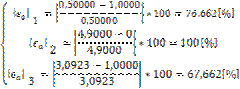
Eroarea relative aproximativa in valoare absoluta este 100.000%
Iteratia #2:
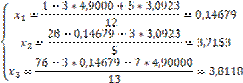
La sfarsitul iteratiei, eroarea relative aproximativa, in valoare absoluta este
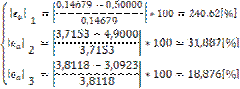
Eroarea relative aproximativa in valoare absoluta maxima este 240.62% care este mult mai mare decat cea obtinuta la prima iteratie 67.612%. Se vede ca solutia converge dupa mai multe iteratii:
|
Iteration |
a1 |
|
a2 |
|
a3 |
|
Se observa o apropiere spre identificare a vectorului de solutie
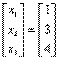
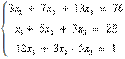
Se
va utilize metoda Gauss-Seidel utilizand ca valori initiale de start ![]()
Rescriind ecuatiile in forma explicita, se obtine
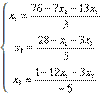
Presupunem vectorul solutiilor initiale de start
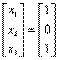
Prin 6 iteratii se obtin rezultatele date mai jos:
|
Iteration |
a1 |
|
a2 |
|
a3 |
|
|
2.0364
-2.0579
|
1.2272
|
4.8144
-4.8653
|
Se poate vedea ca aceasta solutie nu converge si ca matricea coeficientilor nu este dominant diagonal. Matricea coeficientilor:
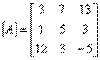
Nu este una de tip dominant diagonal:
![]()
Deci, metoda Gauss-Seidel poate sau nu sa convearga. Totusi, sistemul de ecuatii este acelasi ca in exemplul anterior unde s-a realizat convergenta. Singura diferenta a constat in schimbarea intre ele intre primei ecuatii cu a treia care a condus la faptul ca matricea coeficientilor sa nu mai fie dominant diagonal. Totusi, este posibil ca un system de scuatii sa poata devenii dominant diagonal daca schimbam ecuatiile una cu fiecare cealalta, lucru care nu este posibil in toate cazurile. De exemplu, setul de ecuatii:

Nu poate fi rescris pentru a se obtine o matrice a coeficientilor dominant diagonal.
Prezentare structurii fisierului cod mtl_sle_sim_gaussseidel.m din Matlab
NOTA: Se va demonstra utilizarea mediul de programare Matlab pentru a utilize procedura Gauss-Seidel care utilizeaza o metoda bazata pe tehnici iterative in rezolvarea unui system de ecuatii lineare simultane.
Introducere
Fie,
[A] [X] = [RHS],
Unde [A]nxn reprezinta matricea coeficientilor, [X]nx1 reprezinta matricea vector al solutiei,iar [RHS]nx1 reprezinta termenul liber din dreapta tabelului. iEcuatiile pot fi scrise ca:
x[i] = [rhs[i]-sum(A[i,j]*X*[j])[i<>j]/A[i,j]]
In unele cazuri, precum cel al sistemelor cu un numar mare de ecuatii, mult mai avantajoase pentru calculul ecuatiilor este utilizarea metodelor iterative, precum cea a lui Gauss-Seidel. Metodele de eliminare, precum metoda Gaussian Elimination, genereaza erori de rotunjire in cazul unui numar mare de ecuatii, in raport cu metoda de calcul iterative, precum cea a lui Gauss-Seidel, deoarece utilizatorul poate controla eroarea de rotunjire. Deasemenea, in cazul necunoasterii fenomenul fizic al problemei, alocarea unor valori initiale de start poate fi optimizata pentru o mai rapida convergenta.
Pasii in aplicarea metodei Gauss-Seidel
1) Se aloca valori initiale de start in vectorul solutiilor [X]. Acesasta operatie trebuie bazata pe aspectele fizice ale problemei. (Nota: Pentru start, valorile initiale pot fi considerate ca Xvechi).
X[vechi] = [x1, x2, x3 .. xn]
2) Se inlocuiesc valorile initiale continute in vectorul solutie [X] in sistemul de ecuatii
xi = [RHS[i]-sum(A[i,j]*X[j])[i<>j]/A[i,j]]
3) Noile valori obtinute xi vor inlocui valorile initiale anterioare din vectorul [X] si care vor fi apoi utilizate pentru determinarea unor noi xi prin repetare in pasul 2.
Xvechi = [xnou, x2, x3 .. xn]
Aceasta operatie va fi repetata de n ori pana cand noul vector de solutii [X] va fi completat.
Xnou = [xnou, x2nou, x3nou .. xnnou]
4) In acest moment, prima iteratie este complete si trebuie calculate eroarea relative absoluta, aproximativa (abs_ea) prin comparative cu noile valori initiale din vectorul [X] cu valorile anterioare [Xvechi].
abs_ea_i = 100*|xi nou - xi vechi] /[xi nou]|
Valoarea maxima a acestor erori va reprezenta eroarea absoluta reltiva, aproximativa, la capatul acestei iteratii.
5) Se repeat pasii 1-4, inlocuind noile valori pentru solutii in vectorul solutii vechi in pasul 1, pana cand rezultatul va fi fie stopat de numarul maxim de iteratii, fie s-a atins o tolerant prestabilita
Xvechi = Xnou
Un exemplu de simulare prin metoda Gauss-Seidel
Date de intrare
n = numarul de ecuatii
[A] = nxn matricea coeficientilor
[RHS] = nx1 tabloul termenilor liberi din partea dreapta a ecuatiei
[Xvechi] = nx1 valorile anterioare din vectorul solutii
maxit = numarul maxim de iteratii
NOTA: exista valori de default. Datele de intrare pot fi modificate specificate la inceputul fisierului M
n= 4
A =
RHS =
X =
maxit =
Iteratii
Iteratiile 'maxit' include la sfarsitul fiecarei iteratii, valorile aproximative anterioare, aproximarile prezente, eroarea absoluta relative aproximata procentual si eroarea absoluta relative aproximata procentual cu valoarea maxima.
Iteratia #1
Valorile anterioare iteratiei din vectorul solutie:
Xvechi =
----- ----- ------------Noile valori obtinute iterative ale vectorului solutii----- ----- --------
X =
Coloanele de la 1 pana la 3
Coloana 4
----- ----- -----------Eroarea relative absoluta, aproximata procentual----- ----- ----------
abs_e =
1.0e+002 *
Coloanele de la 1 pana la 3
Coloana 4
----- ----- ---- Eroarea relative absoluta maxima, aproximata procentual ----- ----- ---------
Max_abs_ea =
5.137931034482758e+002
Iteratia #2
Valorile anterioare iteratiei din vectorul solutie
Xvechi =
Columns 1 through 3
Coloana 4
----- ----- ------------ Noile valori obtinute iterative ale vectorului solutii ----- ----- ---------
X =
Coloanele de la 1 pana la 3
Coloana 4
----- ----- ----------- Eroarea relative absoluta, aproximata procentual ----- ----- ----------
abs_e =
1.0e+003 *
Coloanele de la 1 pana la 3
Coloana 4
----- ----- ------- Eroarea relative absoluta maxima, aproximata procentual ----- ----- --------
Max_abs_ea =
9.675135548893273e+003
Iteratia #3
Valorile anterioare iteratiei din vectorul solutie
Xvechi =
Coloanele de la 1 pana la 3
Coloana 4
----- ----- ------------ Noile valori obtinute iterative ale vectorului solutii ----- ----- ----------
X =
Coloanele de la 1 pana la 3
Coloana 4
----- ----- ----------- Eroarea relative absoluta, aproximata procentual ----- ----- -----------
abs_e =
1.0e+002 *
Coloanele de la 1 pana la 3
Coloana 4
----- ----- ------- Eroarea relative absoluta maxima, aproximata procentual ----- ----- ---------
Max_abs_ea =
1.249508350860206e+002
Iteratia #4
Valorile anterioare iteratiei din vectorul solutie
Xvechi =
Coloanele de la 1 pana la 3
Coloana 4
----- ----- ------------ Noile valori obtinute iterative ale vectorului solutii ----- ----- ----------
X =
Coloanele de la 1 pana la 3
Coloana 4
----- ----- ----------- Eroarea relative absoluta, aproximata procentual ----- ----- -----------
abs_e =
Coloanele de la 1 pana la 3
Coloana 4
----- ----- ------- Eroarea relative absoluta maxima, aproximata procentual ----- ----- ---------
Max_abs_ea =
Iteratia #5
Valorile anterioare iteratiei din vectorul solutie
Xvechi =
Coloanele de la 1 pana la 3
Coloana 4
----- ----- ------------ Noile valori obtinute iterative ale vectorului solutii ----- ----- ----------
X =
Coloanele de la 1 pana la 3
Coloana 4
----- ----- ----------- Eroarea relative absoluta, aproximata procentual ----- ----- -----------
5/21/07 3:20 PM MATLAB Command Window 7 of 7
abs_e =
Coloanele de la 1 pana la 3
Coloana 4
----- ----- ------- Eroarea relative absoluta maxima, aproximata procentual ----- ----- ---------
Max_abs_ea =
3. Codul programului mtl_sle_sim_gaussseidel.m cu rulare in Matlab
clc
%Click pe butonul run de pe fereastra de comaanda window
%Acestea reprezinta intrarile ce pot fi modificate de utilizator
%n = numarul de ecuatii'))
n=4;
%[A] = nxn matricea coeficientilor
A=[10,3,4,5;2,24,7,4;2,2,34,3;2,5,2,12];
%[RHS] = nx1 tabloul termenilor liberi din dreapta ecuatiei
RHS=[22,32,41,18];
%[X] = nx1 matricea vector a solutiei cu valorile initiale de start
X=[1,23,4,50];
%maxit = numarul maxim de iteratii
maxit=5;
disp('Simularea prin metoda Gauss-Seidel ')
disp(sprintf('nNOTA: Acest worksheet demonstreaza utilizarea mediului de programare Matlab pentru prezentarea metodei Gauss-Seidel,nan tehnica iterative utilizata in rezolvarea sistemului de ecuatii lineare simultane.'))
disp(sprintf('n ** ** ******Introducere ** ** ********'))
disp(sprintf('nGauss-Seidel metoda utilizata pentru rezolvarea unui set de ecuatii lineare simultane,n[A] [X] = [RHS],unde [A]nxn reprezinta matricea patratica a coeficientilor, [X]nx1 reprezinta Solutianvector, iar [RHS]nx1 reprezinta tabloul termenilor liberi din dreapta.Cele n ecuatii pot fi rescrise ca:'))
disp(sprintf('nx[i]=rhs[i]-sum(A[i,j]*X*[j])[i<>j]/A[i,j]](1.1)'))
disp(sprintf('nIn anumite cazuri, precum cazukl unui system cu un numar ridicat de ecuatii, metodele iterative denrezolvare a ecuatiilor, precum metoda Gauss-Seidel sunt mult mai avantajoase.'))
disp(sprintf('Metodele de eliminare, precum cea Gaussiana, sunt inclinate spre erori de rotunjire pentru unnset mare de ecuatii impugn metode iterative,'))
disp(sprintf('Pornind da la faptul ca metoda Gauss-Seidel, permite utilizatorului controlul erorii de rotunjire.'))
disp(sprintf('Deasemenea, daca fenomenul fizic al problemei este unul bine cunoscut, valorile initiale de start necesare in metodele iterativepot fi alese mult mai judicious pentru o conveergenta mai rapida.'))
disp(sprintf('Pasii de aplicare a metodei Gauss-Seidel:'))
disp(sprintf('1) Se face o apreciere initiala pentru vectorul de solutie [X]. Aceasta poate fi bazate pe fenomenul fizic al nproblemei.n(Nota: Pentru start, trebuiesc considerate valorile initiale de start Xvechi).'))
disp(sprintf('nX[vechi]=[x1,x2,x3..xn] (1.2)'))
disp(sprintf('n2) Se inlocuiesc valorile atribuite initial in vectorul de solutie [X] in ecuatie (1.1).'))
disp(sprintf('n xi = [RHS[i]-sum(A[i,j]*X[j])[i<>j]/A[i,j]] (1.3)'))
disp(sprintf('n3) Noile valori obtinute xi vor inlocui pe cele anterioarein vectorul [X].'))
disp(sprintf('n Xvechi = [xnou, x2, x3 .. xn] (1.4)'))
disp(sprintf('[X] va fi apoi utilizat pentru calculul valorilor xi urmatoare prin repetarea pasului 2.nAcesta va fi repetatde n ori pana ce vectorul [X] este completat cu noile solutii.'))
disp(sprintf('nXnou = [xnou, x2nou, x3nou .. xnnou] (1.5)'))
disp(sprintf('4) in acest punct, prima iteratie este completata si eroarea relativanapproximativa in valoare absoluta (abs_ea) este calculate prin comparatia intre noua solutie din [X] cunvaloarea anterioara [Xvechi].'))
disp(sprintf('n abs_ea_i = 100*|xi nou - xi vechi] /[xi nou]| (1.6)'))
disp(sprintf('nMaximul acestei erori este eroarea aproximativa relative, in valoare absoluta, la sfarsitul celei de-aniteratie.'))
disp(sprintf('n5) Se repeat pasii 1-4, inlocuid vectorul cu solutii vechi prin vectorul cu solutii noi ndin pasul 1. Se repeat pan ace obtinem fie numarul maxim de iteratii fie se obtinentoleranta predefinita.'))
disp(sprintf('nXvechi = Xnou (1.7)'))
disp(sprintf('nA urmeaza simularea metodei Gauss-Seidel.'))
disp(sprintf(' ** ** ***** Date de intrare ** ** ***********'))
disp(sprintf('n = numarul de ecuatii'))
disp(sprintf('[A] = nxn matricea coeficientilor'))
disp(sprintf('[RHS] = nx1 tablou cu termenii liberi din partea dreapta'))
disp(sprintf('[Xold] = nx1 valorile initiale de start din vectorul solutii))
disp(sprintf('maxit = numarul maxim de iteratii'))
disp(sprintf('nNOTA: Acestea sunt valori de default. Datele de intrare pot fi modificate la pornirea celei de-ana fisierului Mn'))
disp(sprintf('n= %d',n))
A
RHS
X
maxit
disp(sprintf(' ** ** *********** Iteratii ** ** **********n'))
disp(sprintf('Below, 'maxit' iterations are conducted and values of the previous approximations, presentnapproximations,absolute relative percentage approximate error, and maximum absolutenrelative percentage approximate error are calculated at the end of each iteration.n'))
%Initializarea tabloului cu erorile aproximative relative in valoare absoluta
abs_ea=zeros(n);
%Iteratii
%Definirea numarului de iteratii ce trebuiesc realizate.
for k=1:maxit
disp(' = = = = = = = = = = = = = = = = = = = = = = = = =')
disp(' = = = = = = = = = = = = = = = = = = = = = = = ==')
disp(' ')
disp(sprintf('Iteration number%d',k))
disp(sprintf('Valorile anterioare iteratiei in vectorul de solutii'))
Xold=X;
Xold
%Urmeaza i bucle care genereaza noul vector al solutiei:
for i=1:n
%Initializarea seriei de sume la zero.
summ=0;
for j=1:n
%Adaugand numai termenul i<>.
if (i<j)
%Generarea termenului de insumare.
summ=summ+A(i,j)*X(j);
end
if (i>j)
%Generarea termenului de insumare.
summ=summ+A(i,j)*X(j);
end
end
%Utilizand metoda Gauss-Seidel pentru a calcula noii termeni [X].
X(i)=(RHS(i)-summ)/A(i,i);
end
%Initializare eroare relative aproximativa in valoare procentuala absoluta, la zero.
Max_abs_ea=0.0;
%Urmeaza i bucle care genereaza eroarea relative aproximativa in valoare absoluta in procente maxime pentru pasul al kth:
for i=1:n
%calculul in procente al erorii aproximative relative pentru fiecare Xi.
abs_ea(i)=abs((X(i)-Xold(i))/X(i))*100.0;
%Definirea valorii maxime al erorii relatrive aproximative.
if abs_ea(i)>Max_abs_ea
Max_abs_ea=abs_ea(i);
end
end
disp(sprintf('-------Noile valori iterative ale vectorului solutie----------'))
X
disp(sprintf('------ Eroarea relative aproximativa in valoare absoluta -----'))
Y=rot90(abs_ea);
abs_e=Y(n,1:n)
disp(sprintf('---Eroarea relative aproximativa in valoare absoluta maxima---'))
Max_abs_ea
End
Rezultatul simularii - Simulation metodei Gauss-Seidel prin programul mtl_sle_sim_gaussseidel.m
NOTA: Acest worksheet demonstreaza utilizarea mediului Matlab pentru a ilustra metoda Gauss-Seidel, ca o tehnica de iteratie utilizata in rezolvarea unui system de ecuatii lineare simultane.
Introducere
Metoda Gauss-Seidel este utilizata pentru rezolvarea unui set de ecuatii lineare simultane, [A] [X] = [RHS], unde [A]nxn reprezinta matricea patratica a coeficientilor, [X]nx1 reprezinta vectorul solutiilor,iar [RHS]nx1 reprezinta tabloul termenilor liberi din dreapta. Ecuatiile pot fi scrise ca:
x[i] = [rhs[i]-sum(A[i,j]*X*[j])[i<>j]/A[i,j]]
In anumite cazuri, precum cel al unui system cu numar mare de ecuatii, metodele iterative de rezolvare a ecuatiilor, precum metoda Gauss-Seidel sunt mul;t mai avantajoase. Metodele de eliminare, precum cea Gaussiana sunt afectate de erorile de rotunjire pentru un numar mare de ecuatii, fata de metoda Gauss-Seidel care permite utilizatorului controlul erorii de rotunjire. Daca fenomenul fizic al problemei este bine cunoscut, valorile initiale de start, necesare metodei iterative, pot fi alese judicious pentru o convergenta mai rapida. Pasii in aplicarea metodei Gauss-Seidel sunt:
1) Se atribuie valori initiale de start pentru vectorul solutii [X], care se poate baza pe fenomenul fizic al problemei. (Nota: Pentru pornire, sunt considerate Xvechi).
X[vechi] = [x1, x2, x3 .. xn]
2) Se inlocuiesc solutiile din vectorul de start [X] in ecuatie.
xi = [RHS[i]-sum(A[i,j]*X[j])[i<>j]/A[i,j]]
3) Noua valoare xi obtinuta va inlocui pe cea anterioara din vectorul solutie [X].
Xvechi = [xnou, x2, x3 .. xn]
Si care va fi utilizat in calculul urmatoarei valori xi prin repetarea pasului 2. Acesta va fi repetat de n ori pana cand noul vector al solutiilor [X] este complet.
Xnou = [xnou, x2nou, x3nou .. xnou]
4) In acest punct, iteratia este complete si este calculate eroarea aproximativa relative in valoare absoluta (abs_ea) comparand noile valori din [X] cu cele continute anterior in [Xvechi].
abs_ea_i = 100*|xi nou - xi vechi] /[xi nou]|
Maximul acestor erori, reprezinta eroarea aproximativa relative in valoare absoluta la sfarsitul iteratiei.
5) Se repeta pasii 1-4, inlocuind vechile solutii cu cele noi in vectorul solutie din pasul 1. Se repeat pana cand se obtine, fie numarul maxim de iteratii, fie este atinsa tolerant predefinita.
Xvechi = Xnou
Urmeaza simularea metodei Gauss-Seidel
Date de intrare
n = numarul de ecuatii
[A] = nxn matricea coeficientilor
[RHS] = nx1 tabloul termenilor liberi din partea dreapta
[Xold] = nx1 vectorul solutii cu valorile initiale de start
maxit = numarul maxim de iteratii
NOTA: Acestea sunt valori de default. Datele de intrare pot fi modificate la pornirea fisierului M
n= 4
A =
10 3 4 5
2 24 7 4
2 2 34 3
2 5 2 12
RHS =
22 32 41 18
X =
1 23 4 50
maxit =
5
Iteratii
Sunt realizate 'maxit' iteratii si la capatul fiecarei iteratii sunt calculate valorile aproximative anterioare, aproximarile prezente, eroarea aproximativa relatiova in valoare absoluta, data in procente, si eroarea aproximativa relatiova in valoare absoluta maxima, data in procente.
Iteratia #1
Valorile anterioare iteratiei al vectorului solutie
Xvechi =
1 23 4 50
----- ----- ------------Noi valori iterative ale vectorului solutie----- ----- -------------
X =
-31.3000 -5.5583 -1.0377 9.2056
----- ----- ----------- Eroarea aproximativa relatiova in valoare absoluta, data in procente ----- ----- -----------
abs_e =
103.1949 513.7931 485.4511 443.1479
----- ----- ------- Eroarea aproximativa relatiova in valoare absoluta maxima, data in procente ----- ----- -------
Max_abs_ea =
513.7931
Iteratia #2
Valorile anterioare iteratiei al vectorului solutie
Xvechi =
-31.3000 -5.5583 -1.0377 9.2056
----- ----- ------------ Noi valori iterative ale vectorului solutie ----- ----- -------------
X =
-0.3202 0.1284 0.4049 1.4324
----- ----- ----------- Eroarea aproximativa relatiova in valoare absoluta, data in procente ----- ----- -----------
abs_e =
1.0e+003 *
9.6751 4.4280 0.3563 0.5427
----- ----- ------- Eroarea aproximativa relatiova in valoare absoluta maxima, data in procente ----- ----- -------
Max_abs_ea =
9.6751e+003
Iteratia #3
Valorile anterioare iteratiei al vectorului solutie
Xvechi =
-0.3202 0.1284 0.4049 1.4324
----- ----- ------------ Noi valori iterative ale vectorului solutie ----- ----- -------------
X =
1.2833 0.8696 0.9529 0.7650
----- ----- ----------- Eroarea aproximativa relatiova in valoare absoluta, data in procente ----- ----- -----------
abs_e =
124.9508 85.2310 57.5062 87.2418
----- ----- ------- Eroarea aproximativa relatiova in valoare absoluta maxima, data in procente ----- ----- -------
Max_abs_ea =
124.9508
Iteratia #4
Valorile anterioare iteratiei al vectorului solutie
Xvechi =
1.2833 0.8696 0.9529 0.7650
----- ----- ------------ Noi valori iterative ale vectorului solutie ----- ----- -------------
X =
1.1755 0.8300 1.0204 0.7882
----- ----- ----------- Eroarea aproximativa relatiova in valoare absoluta, data in procente ----- ----- -----------
abs_e =
9.1730 4.7716 6.6208 2.9450
----- ----- ------- Eroarea aproximativa relatiova in valoare absoluta maxima, data in procente ----- ----- -------
Max_abs_ea =
9.1730
Iteratia #5
Valorile anterioare iteratiei al vectorului solutie
Xvechi =
1.1755 0.8300 1.0204 0.7882
----- ----- ------------ Noi valori iterative ale vectorului solutie ----- ----- -------------
X =
1.1487 0.8086 1.0212 0.8014
----- ----- ----------- Eroarea aproximativa relatiova in valoare absoluta, data in procente ----- ----- -----------
abs_e =
2.3286 2.6396 0.0765 1.6498
----- ----- ------- Eroarea aproximativa relatiova in valoare absoluta maxima, data in procente ----- ----- -------
Max_abs_ea =
5. Prezentare structurii fisierului cod mtl_sle_sim_convgaussseidel.doc din Matlab
NOTA: Acest worksheet demonstreaza convergenta metodei Gauss-Seidel,o tehnica iterative utilizata in rezolvarea unui system de ecuatii lineare simultane.
** ** ** ** **Introducere ** ** ** **
Metoda Gauss-Seidel reprezinta o metoda avantajoasa de rezolvare a unui system de ecuatii lineare simultane deoarece permite utilizatorului controlul erorii de rotunjire, inerenta in metodele de eliminare precum cea Gaussiana. Totusi, aceasta metoda nu este fara capcane. Metoda Gauss-Seidel este o tehnica iterattiva a carei solutie poate sau nu sa convearga. Convergenta este asigurata numai daca matricea coeficientilor,[A]nxn, este dominant diagonala, in caz contrar metoda poate sau nu sa convearga. O matrice a coeficientilor dominant diagonala [A] este definite dupa cum urmeaza:
(Sum(|A(i, j)|, j = 1 .. n),[i <> j] <= |(a(i, i))| (1.1)
Pentru toti i, si
(Sum(|A(i, j)|, j = 1 .. n),[i <> j] < |(a(i, i))| (1.2)
Pentru cel putin un i.
Din fericire, multe sisteme fizice rezulta in ecuatii lineare simultane are matricea coeficientilor dominant diagonal, sau prin schimbarea catorva ecuatii matricea coeficientilor poate devenii dominant diagonala.
Simularea care urmeaza ilustreaza convergenta metodei Gauss-Seidel.
** ** ** ** ******Date de intrare ** ** *************
n = numarul de ecuatii
[A] = nxn matricea coeficientilor
[RHS] = nx1 tabloul termenilor liberi din dreapta
[Xold] = nx1 vectorul solutii cu valori initiale de start
maxit = numarul maxim de iteratii
NOTA: Acestea sunt valori default. Datele de intrare pot fi modificatela startarea fisierului M
n= 4
A =
RHS =
X =
maxit =
** ** ********* Procedura Gauss-Seidel ** ** **********
Metoda Gauss-Seidel utilizeaza ecuatia
x[i] = [rhs[i]-sum(A[i,j]*X*[j])[i<>j]/A[i,j]] (3.1)
pentru a calcula o valoare aproximativa pentru un vector al solutiei [X]. Urmatoarea procedura utilizeaza metoda Gauss-Seidel de calcul al valorii solutiei pentru sistemul de mai sus de ecuatii utilizand maxit iteratii.Apoi, fiecare solutie aproximata este Xi, este memorata dupa fiecare iteratie intr-o matrice cu maxit coloane. Dupa aceia, Matlab va reprezenta solutiile graphic ca o functie de numarul de iteratii.
** ** ** ** ******* Rezultate ** ** ** **
Urmatoarea matrice memoreaza valoarea solutiei pentru Xi in al ith rand dupa fiecare iteratie data.
Xstore =
Urmatoarea matrice memoreaza eroarea relative aproximativa in valoare absoluta maxima, in procente, dupa fiecare iteratie data.
epsmax =
>>
Codul programului mtl_sle_sim_convgaussseidel.m cu rulare in Matlab
clc
%Click pe butonul de run si din fereastra de comanda
%Acestea sunt schimbarile ce pot fi modificate de utilizator
%n = numarul de ecuatii
n=4;
%[A] = nxn matricea coeficientilor
A=[12,7,3,1;1,5,1,2;2,7,-11,1;9,2,1,13];
%[RHS] = nx1 tabloul termenilor liberi din partea dreapta
RHS=[22;7;-2;3];
%[X] = nx1 valorile initiale de start din vectorul solutii
X=[1;2;1;1];
%maxit = numarul maxim de iteratii
maxit=8;
disp('Convergenta metodei Gauss-Seidel')
disp(sprintf('nNOTA: Acest worksheet demonstreaza convergenta metodei Gauss-Seidel,no tehnica iterative utilizata in rezolvarea unui system de ecuatii simultane necuatii lineare.n'))
%----- ----- --------- ----- ------ Introducere----- ----- --------- ----- ----
disp(sprintf(' ** ** ******** Introducere ** ** *******nn '))
disp(sprintf('Metoda Gauss-Seidel este avantajoasa pentru rezolvarea unui sistem '))
disp(sprintf('de ecuatii lineare simultane deoarece permit utilizatorului un control'))
disp(sprintf(eroarea de rotunjire inerenta in metodele de eliminare precum '))
disp(sprintf('eliminarea Gaussiana. dotusi, aceasta metoda nu este fara capcanele ei.'))
disp(sprintf('Metoda Gauss-Seidel reprezinta o tehnica iterative a carei solutie poate sau'))
disp(sprintf('nu sa convearga.convergenta este asigurata numai daca matricea coeficientilor,'))
disp(sprintf('[A]nxn, este dominant diagonala, in caz contrar metoda poate sau nu '))
disp(sprintf('sa convearga.'))
disp(sprintf('nA matricea patratica [A] dominant diagonal este definite cum urmeaza:'))
disp(sprintf('n (Sum(|A(i, j)|, j = 1 .. n),[i <> j] <= |(a(i, i))| (1.1)'))
disp(sprintf('n pentru toti i, si'))
disp(sprintf('n (Sum(|A(i, j)|, j = 1 .. n),[i <> j] < |(a(i, i))| (1.2)'))
disp(sprintf('npentru cel putin un i.'))
disp(sprintf('ndin fericire, multe sisteme fizice care rezulta in ecuatii lineare simultane'))
disp(sprintf('care au matricea coeficientilor dominant diagonala, sau prin'))
disp(sprintf('schimbarea catorva ecuatii, matricea coeficientilor poate devenii'))
disp(sprintf('dominant diagonala.'))
disp(sprintf('Simularea care urmeaza ilustreaza convergentanMetodei Gauss-Seidel.'))
%----- ----- --------- ----- -------Date de intrare ----- ----- --------- ----- --------
disp(sprintf('n ** ** ********* date de intrare ** ** ***nn'))
disp(sprintf('n = numarul de ecuatii'))
disp(sprintf('[A] = nxn matricea coeficientilor'))
disp(sprintf('[RHS] = nx1 tabloul termenilor liberi din partea dreapta'))
disp(sprintf('[Xold] = nx1 valorile de start initiale din vectorul solutie'))
disp(sprintf('maxit = numarul maxim de iteratii'))
disp(sprintf('nNOTA: Acestea sunt valori default. Datele de intrare pot fi modificate la theninitiere a fisierului Mn'))
disp(sprintf('n= %d',n))
A
RHS
X
maxit
%----- ----- ----- ----- -----Procedura Gauss-Siedel ----- ----- ----- ----- -------
disp(sprintf('n ** ** * Procedura Gauss-Seidel ** ** **nn'))
disp(sprintf('Metoda Gauss-Seidel utilizeaza ecuatiin'))
disp(sprintf('n x[i] = [rhs[i]-sum(A[i,j]*X*[j])[i<>j]/A[i,j]] (3.1)'))
disp(sprintf('npentru a calcula o valoare aproximativa pentru vectorul solutii [X].'))
disp(sprintf('Urmatoarea procedura utilizeaza metoda Gauss-Seidel de calcul al valorii'))
disp(sprintf('al solutiei pentru sistemul de ecuatii care utilizeaza maxit iteratii.'))
disp(sprintf('Acesta va memora fiecare solutie aproximativa, Xi, in urma fiecarei iteratii '))
disp(sprintf('intr-o matrice cu maxit coloane. Ulterior, Matlab va reprezenta graphic solutiile'))
disp(sprintf(' ca o functie de numarul de ecuatii.'))
%epsa reprezinta tabloul care memoreaza eroarea relative aproximativa in valoare absoluta la capatul fiecarei iteratii.
epsa=zeros(n);
%Xnew reprezinta vectorul solutii reactualizat dupa fiecare iteratie.
Xnew=zeros(n);
%epsmax reprezinta eroarea relative aproximativa cea mai mare din toate valorile din vectorul de solutii generate in iteratia data.
epsmax=zeros(maxit);
%Xstore reprezinta o matrice care memoreaza vectorului solutie dupa fiecare iteratie.
Xstore=zeros(n,maxit);
%Defineste valorile initiale de start al vectorului solutie.
Xprev=X;
%realizeaza maxit iteratii.
for k=1:maxit
epsmax(k)=0.0;
for i=1:n
%Se initializeaza seria de insumare la valoarea zero.
summ=0.0;
for j=1:n
%Adaugand numai termenii i<>j.
if (i>j)
% Genereaza termenul de insumare din ecuatie (3.1).
summ=summ+A(i,j)*Xprev(j);
end
if (i<j)
%Genereaza termenul de insumare din ecuatie (3.1).
summ=summ+A(i,j)*Xprev(j);
end
end
%Using Equation (3.1) to calculate the new [X] solution vector.
Xnew(i)=(RHS(i)-summ)/A(i,i);
%Se calculeaza eroarea relative aproximativa in valoare absoluta.
epsa(i)=abs((Xnew(i)-Xprev(i))/Xnew(i))*100.0;
%Se cauta valoarea lui epsa maxima.
if epsmax(k)<=epsa(i)
epsmax(k)=epsa(i);
end
%Updating the previous guess.
Xprev(i)=Xnew(i);
%Storing each value of X for each iteration.
Xstore(i,k)=Xnew(i);
end
end
%----- ----- --------- ----- ------Rezultate-------- ----- ------ -----
disp(sprintf('n ** ** ***********Rezultate ** ** ******nn'))
disp(sprintf(Urmatoarea matrice memoreaza valoarea solutiei pentru Xinin the randul al ith dupa fiecare iteratie data'))
Xstore1=Xstore;
Xstore=num2str(Xstore1,'%10.5g')
Xstore=Xstore1;
disp(sprintf('nUrmatoarea matrice memoreaza eroarea relative aproximativa in valoare absoluta maximanprocente dupa fiecare iteratie data.'))
Z=(1:maxit);
%Numai pentru a marii display-ul
epsmax1=epsmax;
epsmax=num2str(epsmax1(1:maxit,1)','%10.5g')
epsmax=epsmax1;
%-------- ----- ------ --Reprezentare grafica----- ----- ----- ----- ----
for i=1:n
figure
plot(Z,Xstore(i,1:maxit),'LineWidth',3)
xlabel('Numarul de iteratie')
ylabel(['X',num2str(i)])
title(['Value of X',num2str(i),' as a function of the iteration Number'])
end
ex=epsmax1(1:maxit,1);
figure
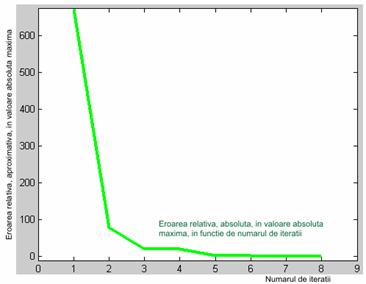
plot(Z,ex,'g','LineWidth',3)
xlabel('Numarul de iteratii')
ylabel('Eroarea relative aproximativa in valoare absoluta maxima')
axis([(0) (maxit+1) (-10) (max(ex))])
title('Eroarea relative aproximativa in valoare absoluta ca functie de numarul de iteratii')
Rezultatul simularii - Convergenta metodei Gauss-Seidel prin programul mtl_sle_sim_convgaussseidel.m
NOTA: This worksheet demonstreaza convergenta metodei Gauss-Seidel, o tehnica iterativa utilizata la rezolvarea unui system de ecuatii lineare simultane.
7.1 Introducere
Metoda Gauss-Seidel este o obtiune avantajoasa pentru rezolvarea unui system de ecuatii lineare simultane deoarece permite utilizatorului sa controleze eroarea de rotunjire, inerenta in cazul metodelor de eliminare, precum cea Gaussian. Totusi, aceasta metoda nu este fara probleme. Metoda Gauss-Seidel reprezinta o tehnica iterative a carei solutie poate sau nu sa convearga. Convergenta este asigurata numai daca matricea coeficientilor, [A]nxn, este dominant diagonala, in caz contrar metoda poate sau nu sa convearga. O matrice patratica dominant diagonal [A] este definite dupa cum urmeaza:
(Sum(|A(i, j)|, j = 1 .. n),[i <> j] <= |(a(i, i))|- pentru orice i, si
(Sum(|A(i, j)|, j = 1 .. n),[i <> j] < |(a(i, i))| - pentru cel putin un i.
Din fericire, multe sisteme fizice care rezulta in ecuatii lineare simultane au matricea coeficientilor dominant diagonal, sau prin schimbarea catorva ecuatii intre ele, matricea coeficientilor poate devenii dominant diagonal. Simularea care urmeaza ilustreaza convergenta metodei Gauss-Seidel.
7.2 Date de intrare
n = numarul de ecuatii
[A] = nxn matricea coeficientilor
[RHS] = nx1 tabloul termenilor liberi din partea dreapta
[Xold] = nx1 vectorul solutii cu valori initiale de start
maxit = numarul maxim de iteratii
NOTA: Acestea sunt valori de default. Datele de intrare pot fi modificate la inceputul fisierului M
n= 4
A =
12 7 3 1
1 5 1 2
2 7 -11 1
9 2 1 13
RHS =
22
7
-2
3
X =
1
2
1
1
maxit =
8
7.3 Procedura Gauss-Seidel Procedure
Metoda Gauss-Seidel utilizeaza ecuatia
x[i] = [rhs[i]-sum(A[i,j]*X*[j])[i<>j]/A[i,j]]
pentru calculul unei valori aproximative pentru un vector de solutie [X]. Urmatoarea procedura utilizeaza metoda Gauss-Seidel de calcul al valorii solutieipentru sistemul de ecuatii de mai sus care utilizeaza maxit iteratii. Apoi, fiecare va fi memorata fiecare solutie aproximativa, Xi, din fiecare iteratie intr-o matrice cu maxit coloane. Dupa aceia, Matlab va imprima rezultatele graphic in functie de numarul de iteratii
7.4 Rezultate
Matricea care urmeaza memoreaza valoarea solutiei pentru Xi din randul al i-lea data dupa fiecare iteratie
Xmemorare =
0.73333 1.0657 1.3274 1.3113 1.2655 1.2613 1.2683 1.27
0.8 1.066 1.1332 1.0994 1.0832 1.0864 1.0895 1.0895
Matricea urmatoare memoreaza erorile aproximative relative, date in valoare absoluta, in procente, date dupa fiecare iteratie.
epsmax =
|
|
|
|
|
|
Probleme de simulare sisteme de ecuatii lineare din ingineria electrica
8.1 Date initiale
Sistemele trifazate de c.a. reprezinta cele mai multe aplicatii industrial. Energia electrica prin current si tensiune furnizata de o companie furnizoare de energie, utilizeaza sisteme de distributie trifazate si un numar mai mare de sarcini trifazate, precum motocompresoarele si similar acestora. Sursele si sarcinile pot fi configurate fie wye (unde sursele sau sarcinile sunt conectate de la conductorul de faza la cel de nul/pamant) fie prin configuratii si combinari intre diferite tipuri obisnuite. Figura de mai jos arata conexiunile unui system trifazat wye-wye modelat complet prin impedante, intalnite in mod obisnuit in orice sistem.
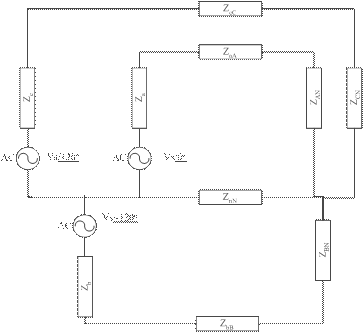
Figura 1. Un system trifazat Wye-Wye cu secventa pozitiva a sarcinii
Pe durata unei analize obisnuite initiaza cele mai multe circuite din textbooks, se considera ca cistemul este complet echilibrat, respective toate sursele, liniile de transport si impedantele sarcinilor sunt echivalente, respective:

Cu
aceasta presupunere, circuitul se reduce in mod obisnuit la un model de circuit
echivalent monofazat, iar circuitul rezultat va fi rezolvat cu o singura
ecuatie pe o bucla. Deoarece, cele 3 impedante de sarcina ![]() si
si![]() nu sunt egale, cu rezultat direct asupra diferentei
curentilor prin fiecare sarcina, masurarea acestora se face in functie de
procentajul diferentei intre curentii pe sarcini. Producerea unui dezechilibru
intr-un system trifazat nu reprezinta o dificultate. Consideram initial sarcina sistemului este la 45 kVA constituita
dintr-un setr de motoare trifazate avand un factor de putere de 0.8 iar
ulterior un electrician conecteaza suplimentar 2 grupuri de cate 1500 W
iluminare, pe A, unul pe faza B si nici unul pe faza C, fapt care genereaza un
dezechilibru in system.
nu sunt egale, cu rezultat direct asupra diferentei
curentilor prin fiecare sarcina, masurarea acestora se face in functie de
procentajul diferentei intre curentii pe sarcini. Producerea unui dezechilibru
intr-un system trifazat nu reprezinta o dificultate. Consideram initial sarcina sistemului este la 45 kVA constituita
dintr-un setr de motoare trifazate avand un factor de putere de 0.8 iar
ulterior un electrician conecteaza suplimentar 2 grupuri de cate 1500 W
iluminare, pe A, unul pe faza B si nici unul pe faza C, fapt care genereaza un
dezechilibru in system.
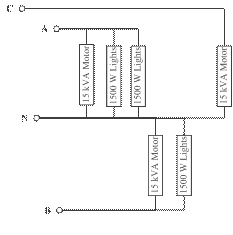
Figura 2. Model pentru sarcina sistemului
Impedanta pentru fiecare sarcina poate fi determinate din exprimarea puterii consummate pe fiecare faza a sistemului.

Converting
these to impedances using the formula ![]() in care potentialul electric
in care potentialul electric ![]() conduce la:
conduce la:

Pentru
restul acestei analize se presupune ca fiecare faza a sistemului dispune de o
sursa independent si o impedanta de linie de ![]() si ca conductorul de
impamantare este
si ca conductorul de
impamantare este ![]() , ceea ce conduce la urmatoarea schema:
, ceea ce conduce la urmatoarea schema:
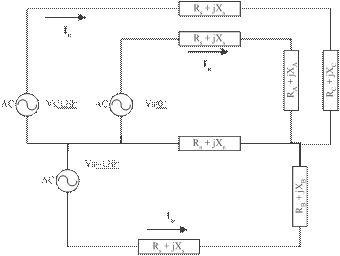
Figura 3. Modelul de circuit echivalent pentru cazul prezentat
Circuitul
poate fi analizat utilizand cele 3 ecuatii de bucla, utilizand curentii ![]() si
si ![]() . Pentru bucla ecuatia
in complex pentru reprezentarea tensiunii este:
. Pentru bucla ecuatia
in complex pentru reprezentarea tensiunii este:
Bucla
A: ![]()
Si
similar pentru B si C. Vom definii
ecuatia buclei A prin 2 ecuatii separate, necomplexe, una penru partea reala
iar cealalta pentru partea imaginara. Utilizand ![]() se obtine:
se obtine:
Partea reala a lui A: ![]()
Partea imaginara a lui A: ![]()
Aplicand aceiasi analiza pentru buclele B si C se obtin:
Partea reala a lui B:![]()
Partea imaginara a lui B:![]()
Partea reala a lui C: ![]()
Partea imaginara a lui C:![]()
Prin urmare, se obtine un system de 6 ecuatii lineare cu 6
necunoscute ![]() ce trebuie rezolvat
prin metode traditionale, respective:
ce trebuie rezolvat
prin metode traditionale, respective:

Figure 4. Sistemul complet de ecuatii
Odata ce curentii au fost determinate, printr-o procedura simpla,
ce utilizeaza legea lui Ohm, se determina tensiunile la bornele motorului ![]() (VAN, VBN,
si VCN).
(VAN, VBN,
si VCN).
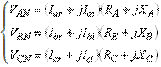
Pentru o mai buna determinare a dezechilibrului, diferenta procentuala a curentilor reali prin elementele de sarcina, este adeseori mai mare decat cea considerate. In cazul unui motor trifazat un dezechilibru semnificativ poate fi datorat defectarii unui rulment sau unei alte piese. Aplicand legea lui Ohm rezulta:
![]()
![]()
unde Z3Ф este
mai usor de calculate decat ![]() . Nu trebuie omis
faptul ca sarcinile de iluminare sunt separate..
. Nu trebuie omis
faptul ca sarcinile de iluminare sunt separate..
10. Utilizarea metodei Gauss-Siedel pentru rezolvarea sistemului de ecuatii lineare simultane
O matrice patratica [A]nxn este dominant diagonal daca:
(A) ![]() i = 1, 2, . , n
i = 1, 2, . , n
(B) ![]() i = 1, 2, . , n si
i = 1, 2, . , n si ![]() pentru orice i = 1, 2, . , n
pentru orice i = 1, 2, . , n
(C) ![]() i = 1, 2, . , n si
i = 1, 2, . , n si ![]() pentru orice i = 1, 2, . , n
pentru orice i = 1, 2, . , n
(D) ![]() i = 1, 2, . , n
i = 1, 2, . , n
2. Utilizand [x1 x2 x3] = [1 3 5] cavalori initiale de start pentru vectorul solutii [x1 x2 x3] dupa un numar de iteratii ale metodei Gauss-Seidel aplicata sistemului:
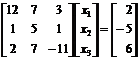
Conduce la urmatoarele rezultate
(A) [-2.8333 -1.4333 -1.9727]
(B) [1.4959 -0.90464 -0.84914]
(C) [0.90666 -1.0115 -1.0242]
(D) [1.2148 -0.72060 -0.82451]
Pentru a se asigura convergenta urmatorului system de ecuatii,

Prin utilizarea metodei Gauss-Seidel in primul rand rescriem ecuatiile dupa cum urmeaza:
(A) 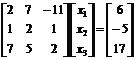
(B) 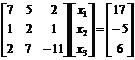
(C) 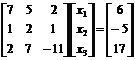
(D) Ecuatiile nu pot fi rescrise pentru a se asigura convergenta.
Pentru  si prin utilizarea
si prin utilizarea ![]() ca valori initiale de
start ale vectorului de solutii
ca valori initiale de
start ale vectorului de solutii ![]() , la capatul
efectuarii iteratiilor se obtine
, la capatul
efectuarii iteratiilor se obtine
|
Iteration # |
x |
x |
x |
La cat speri ca dupa prima iteratie solutia sa fie la cel putin 1 bit semnificativ?
(A)
(B)
(C)
(D)
5. Algoritmul metodei Gauss-Seidel pentru rezolvarea [A] [X] = [C] este dat prin prescrierea a nmax iteratii. Valoarea initiala a lui [X] este memorata in tabloul [X].
(A) Sub Seidel(n
For k = 1 To nmax
For i = 1 To n
For j = 1 To n
If (i <> j) Then
Sum = Sum + a(i, j) * x(j)
endif
x(i) = (rhs(i) - Sum) / a(i, i)
Next i
Next k
End Sub
(B) Sub Seidel(n
For k = 1 To nmax
For i = 1 To n
Sum = 0
For j = 1 To n
If (i <> j) Then
Sum = Sum + a(i, j) * x(j)
endif
x(i) = (rhs(i) - Sum) / a(i, i)
Next i
Next k
End Sub
(C) Sub Seidel(n
For k = 1 To nmax
For i = 1 To n
Sum = 0
For j = 1 To n
Sum = Sum + a(i, j) * x(j)
x(i) = (rhs(i) - Sum) / a(i, i)
Next i
Next k
End Sub
(D) Sub Seidel(n
For k = 1 To nmax
For i = 1 To n
Sum = 0
For j = 1 To n
If (i <> j) Then
Sum = Sum + a(i, j) * x(j)
endif
x(i) = rhs(i) / a(i, i)
Next i
Next k
End Sub
6. Termistorul de masurare a temperaturii are un semnal la iesire nelinear, si sunt calibrate pentru un domeniu limitat. Atunci cand un termistor este fabricat, furnizorul prezinta o curba de variatie a rezistentei in raport cu temperature. O reprezentare precisa a curbei este data in general de relatia:
![]()
unde
T reprezinta temperature in grade absolute [K], R rezistenta electrica in
Ω, iar ![]() sunt constant ale
curbei de calibrare.
sunt constant ale
curbei de calibrare.
|
R |
T |
|
|
|
Valoarea
temperaturii data in ![]() pentru o rezistenta masurata la 900 Ω mult mai apropiata este
pentru o rezistenta masurata la 900 Ω mult mai apropiata este
(A)
(B)
(C)
(D)
|
Politica de confidentialitate |
| Copyright ©
2024 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |