SERII DE NUMERE REALE
Se considera un sir
de numere reale ![]() , cu ajutorul caruia construim sirul
, cu ajutorul caruia construim sirul ![]() , definit de relatia:
, definit de relatia:
![]()
Definitia 1. Cuplul ![]() se numeste serie
de numere reale, unde
se numeste serie
de numere reale, unde ![]() sunt termenii acestei
serii si
sunt termenii acestei
serii si ![]() sirul sumelor partiale.
sirul sumelor partiale.
Cuplul de obiecte
matematice definit mai sus se noteaza in manualele de specialitate cu ![]()
Definitia 2. Seria de numere reale ![]() se numeste
convergenta, daca sirul sumelor partiale este convergent.
se numeste
convergenta, daca sirul sumelor partiale este convergent.
Daca sirul
sumelor partiale ale seriei ![]() are limita,
finita sau nu, pe care o notam cu s, atunci aceasta limita
o vom numi suma seriei.
are limita,
finita sau nu, pe care o notam cu s, atunci aceasta limita
o vom numi suma seriei.
Definitia 3. Daca sirul sumelor partiale corespunzator unei serii (2) nu are limita, in acest caz seria se numeste oscilanta (are mai multe puncte limita).
Definitia 4. O serie de numere reale se numeste convergenta daca sirul sumelor partiale are limita finita si se numeste divergenta daca acest sir are limita infinita.
A stabili natura unei serii de numere reale inseamna a stabili convergenta sau divergenta ei.
Din elementele prezentate mai sus rezulta ca putem stabili natura unei serii calculand limita sirului sumelor partiale.
Studiati natura seriilor de mai jos, calculand limita sirului sumelor partiale:
1. ![]()
Solutie:
![]() este termenul general
al seriei
este termenul general
al seriei
Pentru calculul lui ![]() , descompunem termenul general in fractii simple
dupa cum urmeaza:
, descompunem termenul general in fractii simple
dupa cum urmeaza:
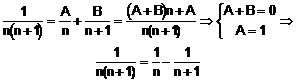
Atunci,
![]()
![]()
![]()
![]()
![]()
Prin urmare, seria este convergenta.
2. 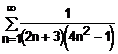
Solutie:
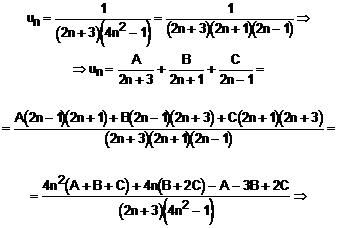
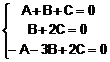
![]()
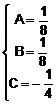
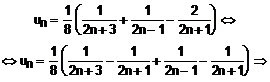
![]() =
=
![]()
![]()
Prin urmare, seria este convergenta.
3.![]()
Solutie:

Prin urmare, seria este divergenta.
4. Urmand modelul prezentat mai sus, stabiliti daca seriile de mai jos sunt convergente:
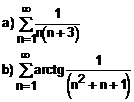
![]()
![]()
Solutie:
a) ![]()
Termenul general al seriei este ![]() , pe care-l descompunem astfel:
, pe care-l descompunem astfel:
![]()
![]() 1 = (A + B)n + 3A
1 = (A + B)n + 3A ![]()
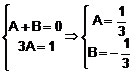
Termenul general se scrie, deci:
![]()
Sirul
sumelor partiale pentru sera data este ![]() , unde:
, unde: ![]()
Vom scrie, conform celor de mai sus:
![]()

Deci, ![]()
![]() seria este
convergenta, cu suma
seria este
convergenta, cu suma ![]() .
.
b) ![]()
Sirul sumelor partiale are
termenul general: ![]()
Avem descompunerea: ![]()
Atunci,
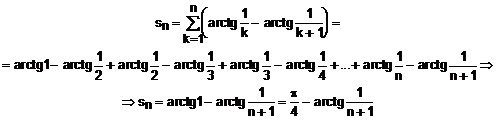
![]() , deci seria este convergenta, cu suma
, deci seria este convergenta, cu suma ![]()
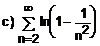
Sirul sumelor partiale are termenul general:
![]()
Prin urmare, ![]() este o suma
de logaritmi pe care o putem scrie:
este o suma
de logaritmi pe care o putem scrie:
![]()
Evaluam produsul:
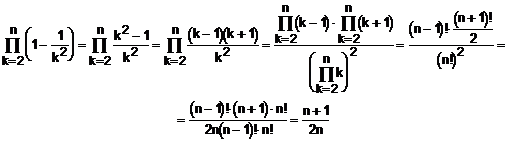
Prin urmare, ![]() , deci seria este convergenta.
, deci seria este convergenta.
Exista situatii cand nu este posibil
sa calculam suma unei serii, iar pentru aceasta vom enunta
diferite criterii de convergenta, care permit determinarea naturii
seriei fara calculul efectiv al limitei lui ![]() .
.
Teorema 1. Daca o serie de numere este convergenta,
atunci sirul ![]() e convergent
catre 0.
e convergent
catre 0.
Reciproc nu este adevarat, in sensul ca exista serii al caror termen general este convergent catre 0, dar ele sunt serii divergente. De exemplu, seria armonica
![]()
![]()
Totusi, se poate
demonstra ca aceasta serie este divergenta, avand suma ![]() .
.
O consecinta a
acestei proprietati, aplicabila in practica, este
urmatoarea: daca intr-o serie data sirul ![]() nu este convergent
catre 0, atunci seria nu este convergenta.
nu este convergent
catre 0, atunci seria nu este convergenta.
Utilizand rezultatul enuntat in consecinta de mai sus, dovediti ca urmatoarele serii sunt divergente:
5. ![]()
Solutie:
![]()
![]()
Prin urmare, seria este divergenta.
6. ![]()
Solutie:
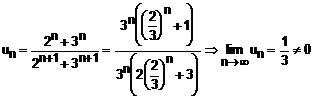
Deci, seria data este divergenta.
Serii cu termeni pozitivi
In situatia in care
termenul general al unei serii, ![]() , este pozitiv, spunem ca seria este cu termeni
pozitivi. Particularitatea unei astfel de serii de numere reale este aceea
ca intotdeauna exista suma ei, finita sau nu. Cu alte cuvinte,
printre seriile cu termeni pozitivi nu vom intalni serii oscilante. Pentru
stabilirea naturii unei serii cu termeni pozitivi avem ca instrumente cateva
criterii de convergenta, dintre care enuntam trei:
, este pozitiv, spunem ca seria este cu termeni
pozitivi. Particularitatea unei astfel de serii de numere reale este aceea
ca intotdeauna exista suma ei, finita sau nu. Cu alte cuvinte,
printre seriile cu termeni pozitivi nu vom intalni serii oscilante. Pentru
stabilirea naturii unei serii cu termeni pozitivi avem ca instrumente cateva
criterii de convergenta, dintre care enuntam trei:
Fie seria de numere reale
cu termeni pozitivi ![]() :
:
Criteriul raportului: Presupunem ca exista ![]() . Atunci:
. Atunci:
Daca l>1, seria este divergenta
Daca l<1, seria este convergenta.
Daca l= 1, nu putem decide asupra naturii seriei utilizand acest criteriu.
Criteriul radacinii: : Presupunem ca
exista![]() . Atunci:
. Atunci:
Daca l>1, seria este divergenta
Daca l<1, seria este convergenta.
Daca l= 1, nu putem decide asupra naturii seriei utilizand acest criteriu.
Criteriul Raabe- Duhamel : Presupunem ca exista
![]() .
.
Atunci:
Daca l<1, seria este divergenta
Daca l>1, seria este convergenta.
Daca l= 1, nu putem decide asupra naturii seriei utilizand acest criteriu.
7. Studiati,
dupa valorile parametrului real ![]() , natura seriei:
, natura seriei:![]() .
.
Solutie:
Termenul general al seriei
este: ![]() . Aplicam criteriul raportului:
. Aplicam criteriul raportului:
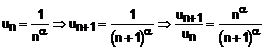
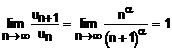
Prin urmare, utilizand criteriul raportului nu putem decide asupra naturii seriei. ?n astfel de situatii, inlocuim acest criteriu cu criteriul Raabe- Duhamel. Calculam:
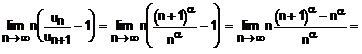
![]()
Atunci, criteriul ne spune ca:
![]() , seria este convergenta
, seria este convergenta
Daca ![]() , seria este divergenta.
, seria este divergenta.
Daca ![]() , obtinem seria armonica, despre care am spus
ca este divergenta.
, obtinem seria armonica, despre care am spus
ca este divergenta.
8. Studiati natura seriei: ![]()
Solutie:
Termenul general este ![]() . Aplicam criteriul raportului:
. Aplicam criteriul raportului:

Seria este, deci, convergenta.
9. Studiati natura seriei, dupa
valorile parametrului a:![]() , a >0.
, a >0.
Solutie:
Aplicam criteriul raportului:
![]()
![]()
?n concluzie, seria este convergenta indiferent de valoarea parametrului pozitiv a.
10. Studiati
natura seriei, dupa valorile parametrului a: ![]()
Solutie:
![]()
Aplicam criteriul radacinii:
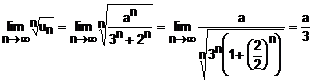
Evident, daca a< 3, seria este convergenta si daca a>3, seria este divergenta. Pentru a= 3, seria devine:
![]() .
.
Pentru aceasta serie, studiul convergentei cu ajutorul criteriului raportului este irelevant (tema), de aceea aplicam criteriul Raabe- Duhamel:
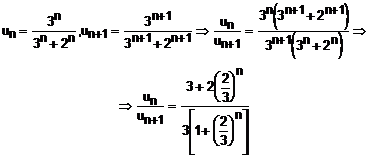

Limita rezultata fiind subunitara, seria este divergenta.
11. Studiati,
dupa valorile parametrului a, natura seriei: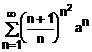
Solutie:
Aplicam criteriul radacinii pentru termenul general al seriei,
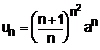 .
.
![]() .
.
Prin urmare, daca
ae< 1, deci daca ![]() , seria este convergenta. Daca
, seria este convergenta. Daca ![]() , seria este divergenta.
, seria este divergenta.
12. Studiati
natura seriei: 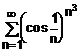
Solutie:
Aplicam criteriul
radacinii pentru termenul general : 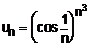
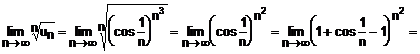
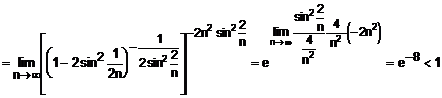
Deci, seria este convergenta.
Criteriul logaritmic: Pentru seria de numere reale pozitive ![]() , se calculeaza
, se calculeaza 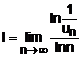 si decidem:
si decidem:
Daca l>1, seria este convergenta
Daca l<1, seria este divergenta.
Daca l= 1, nu putem decide asupra naturii seriei utilizand acest criteriu.
Folosind criteriul logaritmic, sa se studieze natura seriilor:
13. ![]() .
.
Solutie:
Termenul general al seriei
este: ![]()
Calculam limita
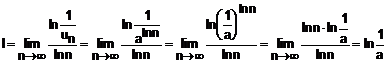

14. 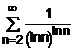
Solutie:
Termenul general este ![]() . Calculam limita:
. Calculam limita:
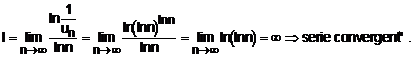
Serii alternate si serii absolut convergente
Serii alternate
Definitia 5. Se numeste serie alternata, o serie de forma:
![]() ,
,
sau de forma
![]() .
.
Criteriul lui Leibniz Daca sirul ![]() este descrescator
si tinde la zero, atunci seria alternata este convergenta.
este descrescator
si tinde la zero, atunci seria alternata este convergenta.
Serii absolut convergente
Definitia 6. Spunem ca o serie ![]() este absolut
convergenta, daca seria
este absolut
convergenta, daca seria ![]() este convergenta.
este convergenta.
Se poate demonstra ca daca o serie este absolut convergenta, atunci ea este si convergenta. Reciproca acestei afirmatii nu este adevarata, dupa cum se va vedea din exemplul de mai jos:
15. Studiati convergenta si absolut convergenta seriei alternate de mai jos:
![]()
Solutie:
Seria data in enunt
are ca termen general ![]() . Este evident ca
. Este evident ca ![]() . Prin urmare, criteriul lui Leibniz ne asigura ca
aceasta serie este convergenta. Sa verificam absolut
convergenta sa:
. Prin urmare, criteriul lui Leibniz ne asigura ca
aceasta serie este convergenta. Sa verificam absolut
convergenta sa:
Privita ca serie de
numere reale, termenul general al seriei date este ![]() si seria
si seria
![]()
este tocmai seria armonica despre care stim ca este divergenta.
Iata, deci, in acest exemplu, ca o serie care este convergenta nu este in mod necesar si absolut convergenta. Aceasta serie data in enuntul problemei poarta numele de serie armonica alternata.
Teorema lui Dirichlet Intr-o serie alternata convergenta, cu suma egala cu s, oricum am schimba ordinea termenilor sai, seria obtinuta este tot absolut convergenta si are aceeasi suma, s.
Daca, insa, o serie este doar convergenta, fara a fi absolut convergenta, prin schimbarea ordinii termenilor ei se obtin serii care fie au alta suma, fie sunt chiar divergente sau oscilante.
16. Seria armonica alternata discutata mai sus face parte din categoria seriilor convergente, dar nu absolut convergente, care modificata astfel ca dupa un termen pozitiv al sau sa urmeze doi termeni negativi, conduce la o serie care are suma egala cu jumatate din suma seriei armonice alternate:
![]() seria armonica
alternata
seria armonica
alternata
![]() seria modificata
dupa regula expusa mai sus.
seria modificata
dupa regula expusa mai sus.
17. Stabiliti
natura seriei alternate: ![]() .
.
Solutie:
Seria modulelor este: ![]() , cu termenul general
, cu termenul general ![]() . Studiem convergenta acestei serii cu ajutorul
criteriului raportului:
. Studiem convergenta acestei serii cu ajutorul
criteriului raportului:
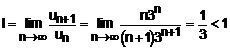
Prin urmare, seria modulelor este convergenta, deci seria data in enunt este absolut convergenta. Din rezultatele teoretice prezentate nai sus, rezulta ca seria este si convergenta.
18. Studiati convergenta si absolut convergenta seriei alternate de mai jos:
![]() .
.
Solutie:
Seria modulelor este ![]() , cu termenul general
, cu termenul general ![]() . Studiem convergenta ei aplicand criteriul raportului:
. Studiem convergenta ei aplicand criteriul raportului:
![]()
Rezultatul este irelevant, deci aplicam criteriul Raabe- Duhamel:
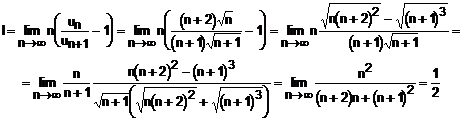
Limita fiind
subunitara, seria modulelor este divergenta. Prin urmare, seria
data nu este absolut convergenta. Totusi, se observa
ca termenul general al seriei alternate date in enunt este convergent
catre 0 si se verifica faptul ca este monoton
descrescator, evaluand diferenta ![]() . Din criteriul Leibnitz deducem ca seria alternata
este convergenta.
. Din criteriul Leibnitz deducem ca seria alternata
este convergenta.
19. Studiati natura seriilor alternante:
a)
![]()
b) ![]()
Solutie:
a) Seria modulelor este: ![]() , cu termenul general
, cu termenul general ![]() . Studiem convergenta ei, ca serie cu termeni pozitivi,
aplicand criteriul Raabe Duhamel. Criteriul raportului, aplicabil in acest caz,
nu conduce la nici un rezultat.
. Studiem convergenta ei, ca serie cu termeni pozitivi,
aplicand criteriul Raabe Duhamel. Criteriul raportului, aplicabil in acest caz,
nu conduce la nici un rezultat.
Calculam:
![]() , unde:
, unde:
![]()
![]() ,
,
deci seria modulelor este convergenta. Conform definitiei, seria din enunt este absolut convergenta.
Elementele de teorie ne asigura ca seria din problema, fiind absolut convergenta, este si convergenta.
b) Seria
modulelor este: ![]() , cu termenul general
, cu termenul general ![]() . Studiem natura ei, cu criteriul raportului:
. Studiem natura ei, cu criteriul raportului:
![]() ,
,
deci seria din enunt este absolut convergenta, deci si convergenta.
|
Politica de confidentialitate |
| Copyright ©
2024 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |