Definitie : Tetraedrul Crelle este tetraedrul pentru care exista o sfera tangenta la muchiile sale.
Din definitie deducem ca pe aceasta sfera exista patru cercuri inscrise in fiecare fata a tetraedrului (intersectiile planelor cu sfera inscrisa tangenta la muchiile tetraedrului) si sunt tangente doua cate doua.
Teorema 46:( a lui Crelle)
Fiind dat un tetraedru [ABCD] exista o sfera tangenta celor sase muchii ale tetraedrului daca si numai daca au loc conditiile AB + CD = AC + BD = AD + BC.
Demonstratie :
Implicatia " exista sfera, atunci are loc relatia" este evidenta datorita proprietatii de congruenta a tangentelor dintr-un punct exterior.
![]()
 (AC s(AA s(AB )=a
(AC s(AA s(AB )=a
BC s(BB s(BA =b
(CA s(CC s(CB ) =c
(DB s(DA s(DC )=d Atunci:
![]() AB+CD=AC +BC +CC +C D = a+b+c+d
AB+CD=AC +BC +CC +C D = a+b+c+d
AC+BD=AB +CB +BB +DB = a+b+c+d T
AD+BC=AA +A D+BA +A C= a+b+c+d
T AB + CD = AC + AD = AD + BC.
Reciproc , presupunem ca este indeplinita conditia AB + CD = AC + AD = AD + BC T
AB - BC = AD - CD si AC - CD =AB - BD . Se obtine astfel:
AC + AB - BC = AD + AC - CD = AD + AB - BD , deci:
![]() si
si ![]()
Prima relatie arata ca cercul inscris in triunghiul [ABC] are punctul de contact cu [AB] coincident cu punctul de contact cu [AB] al cercului inscris in DABD. Deci exista o sfera ce contine doua cercuri (inscris in DABC si inscris in DABD). Exista ,deci, punctele A ,B ,A ,B , C in sfera care este tangenta segmentelor [BC], [AC], [AD], [BD], [AB]. Se considera planul (BDC) si cercul de intersectie determinat de plan si sfera considerata. Relatia a doua dovedeste ca punctul de contact cu [BC] al cercului inscris in triunghiul [BDC] si punctul de contact cu [BC] al cercului inscris in DABC , coincid. Cu cercul de intersectie dintre planul (BDC) si sfera este tangent muchiilor tetraedrului in B si A , iar pe de alta parte prin B si A trece cercul inscris in triunghiul [BDC], rezulta ca cercul de intersectie dintre planul (BDC) sfera si cercul inscris in triunghiul [BDC] coincid.
Deci sfera este tangenta si muchiei [CD] ceea ce demonstreaza teorema.
Teorema 47:
Perpendicularele duse in centrele cercurilor inscrise in fetele tetraedrului Crelle sunt concurente.
Demonstratie :
Intr-adevar , cercurile inscrise in fetele tetraedrului Crelle sunt sectiuni obtinute prin intersectia fetelor cu sfera; perpendicularele in centrele acestor cercuri pe planul lor se vor intalni intr-un punct. Fie O acest punct; avem (OA s(OB s(OC s(OC s(OB s(OA ). Cum A , B', C , A , B , C sunt puncte de tangenta ale sferei cu muchiile tetraedrului atunci O este centrul sferei Crelle, cum este numita sfera ce este tangenta la muchiile unui tetraedru Crelle.
Teorema 48:
Intr-un tetraedru Crelle dreptele ce unesc punctele de contact ale sferei cu muchiile opuse sunt concurente.
Demonstratie :
 Se foloseste teorema lui Menelaus in spatiu .
Se foloseste teorema lui Menelaus in spatiu .
In tetraedrul Crelle [ABCD] avem : A ,B',C ,A ,B ,C puncte
de contact ale sferei cu muchiile, iar dreptele A A , B B ,C C
ce trec prin punctele de contact ale muchiilor opuse.
Conform celor afirmate rezulta:
![]() [DA s[DB s[DC ]; [AA s[AC s[AB
[DA s[DB s[DC ]; [AA s[AC s[AB
T![]()
[BC s[BB s[BA ; [CA s[CB s[CC
De aici, conform teoremei lui Menelaus in spatiu rezulta ca punctele A ,A ,C',C sunt coplanare si A A C C =. Deci A A B B C C =, ceea ce demonstreaza teorema.
Teorema 49:
Intr-un tetraedru Crelle [ABCD] unde BC=a , CA=b, AB=c AB +BC= s, volumul V si raza r a sferei hexatangente satisfac egalitatea: 3Vr= 2(s-p)(p-a)(p-b)(p-c). (1)
 Demonstratie :
Demonstratie :
Figura alaturata reprezinta o parte din sectiunea in tetraedru
perpendiculara pe [BC] in punctul ei de contact cu sfera
hexatangenta. ![]() s
s![]() IAA ID.
Segmentul A J de lungime r este
IAA ID.
Segmentul A J de lungime r este
diametrul unui cerc a carui coarda se vede de pe cerc sub unghiul
BC, deci r sin2![]() = rA2 + rD2 - 2 rA rD cos
= rA2 + rD2 - 2 rA rD cos![]() (2)
(2)
Calculand prin formula cosinusului in triedrul B se obtine
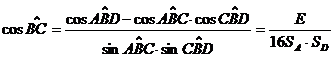 , unde
, unde
E=2a2[c2 -(s - b)2 - (s - a)2] - (a2 -b2 + c2 ) [ a2+(s - b)2 - (s - c)2].
Se mai observa ca semiperimetrul triunghiului [BCD] este PA= s + a -p, deci
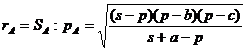
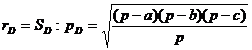
Pentru unghiul diedru ![]() se va utiliza formula:
2 SASDsin
se va utiliza formula:
2 SASDsin![]() =3aV. Amplificand relatia (2) prin 8p(s+a-p) si
operand substitutiile preconizate se obtine:
=3aV. Amplificand relatia (2) prin 8p(s+a-p) si
operand substitutiile preconizate se obtine:
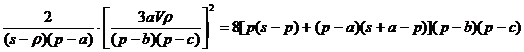
prin calcule algebrice simple membrul drept capata forma
8a2(p - a) S - 8a2p(p - a)= 8a2(p - a)(s - p) si se obtine formula (1).
Observatie :
Formula (1) mascheaza existenta unei valori minime so
a lui s. Pentru s so , V tinde la zero, dar r tinde la ![]() . Pentru s< so muchiile din D au lungimi numere
complexe, V si r sunt numere reale negative , lipsite de
interpretari geometrice , dar (1) ramane formal valabila.
. Pentru s< so muchiile din D au lungimi numere
complexe, V si r sunt numere reale negative , lipsite de
interpretari geometrice , dar (1) ramane formal valabila.
J este in planul (BCD) daca si numai daca ![]() . Daca
. Daca ![]() punctele A si J
vor fi separate de (BCD).
punctele A si J
vor fi separate de (BCD).
Daca r,r,R sunt razele sferelor inscrise, Crelle
si respectiv circumscrisa tetraedrului[ABCD] , atunci r<r ![]() . Egalitatea are loc daca si numai daca
tetraedrul [ABCD] este regulat. Deci vom avea R=r
. Egalitatea are loc daca si numai daca
tetraedrul [ABCD] este regulat. Deci vom avea R=r![]() .
.
Exista modalitati algebrice de a stabili prin calcul
inegalitatile r<r ![]() ; pentru r se foloseste formula r S=3V, iar pentru R formula 6RV=T , unde T este aria unui triunghi care
are ca lungimi de laturi produsele lungimilor muchiilor opuse ale tetraedrului.
; pentru r se foloseste formula r S=3V, iar pentru R formula 6RV=T , unde T este aria unui triunghi care
are ca lungimi de laturi produsele lungimilor muchiilor opuse ale tetraedrului.
|
Politica de confidentialitate |
| Copyright ©
2024 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |