Numeroase proprietati ale triunghiului echilateral extinse in spatiu se intalnesc in tetraedre echifaciale ; iata de ce studiul acestei clase de tetraedre este deosebit de util studiului interferentelor din geometria euclidiana plana si cea a spatiului tridimensional.
Definitie: Se numeste tetraedru echifacial un tetraedru al carui fete sunt echivalente ( au aceeasi arie).
Definitii echivalente
Teorema 29:
Urmatoarele proprietati ale unui tetraedru echifacial sunt echivalente:
Demonstratie:
Demonstratia o vom face in urmatoarea ordine:
T 9 8
7
3
Sa stabilim pe rand toate implicatiile din diagrama
T6 Suma masurilor tuturor unghiurilor plane ale tuturor fetelor tetraedrului este egala cu suma masurilor unghiurilor a patru triunghiuri adica 4 180o=720o, iar suma este aceeasi la fiecare varf , adica la fiecare varf suma este de 180o
T5 Evident
T8 Daca R este raza sferei circumscrise tetraedrului si r este raza sferei inscrise in tetraedru si centrele acestor sfere coincid , atunci punctul de tangenta al sferei inscrisa
cu fiecare fata va fi situat in interiorul sferei si va fi
deportat de fiecare varf al tetraedrului cu
, adica va fi centrul cercului circumscris acestui
triunghi de raza
T4 Perpendicularele din centrul sferei circumscrise cad in centrele cercurilor circumscrise si daca au aceeasi raza inseamna ca centrul sferei circumscrise este la distanta egala de fete, deci este centrul sferei inscrise.
T8 Evident, deoarece toate triunghiurile sunt congruente
T7 Fie poligonul AFCEBD obtinut prin desfasurarea tetraedrului si fie O,O1,O2,O3 centrele cercurilor circumscrise triunghiurilor [ABC],[ABD],[BCE],[ACF]. Notam razele cum R.
DAO3F s DAO1D s DBOC s DBO2C
(L.L.L.) T 
s
s
s
s
s
s
s
=
DDO1F s DBO2E s DAOC s DAO3C
(L.L.L.) T 
s s
s
s
s
s
s
= 
DCO3F s DCO2F s DAOB s DAO1B
(L.L.L.) T 
s
s
s
s
s
s
s
= 
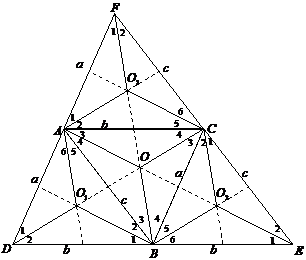
Fig 1 Fig 2
In
DABC m()+m()+m() +m(
)+m()+m()= 180o , adica a b g a b g= 180o;
deci 2a b g= 180o
m(
)=m()+m()+m() +m()+m()+m(), deci F,A,D sunt coliniare.
Analog m(
)=180o; m(
)=180o si deci hexagonul ADBECF nu-i altceva decat triunghiul [DEF] in
care AB,BC, CA sunt linii mijlocii.
T7 In desfasurarea tetraedrului [SABC] ( fig 1) unghiurile hexagonului ADBECF in varfurile A,B,C nu sunt altceva decat suma unghiurilor plane ale fetelor triunghiulare tetraedrului avand varfurile respectiv in A,B,C. Cum insa aceste sume sunt prin ipoteza fiecare egale cu 180o, rezulta ca in cazul precedent hexagonul ADBECF este triunghiul [DEF] in care AB,BC,CA sunt linii mijlocii.
T Din figura 2 ,rezulta,
evident ca m(
)+m(
)+m(
)= m(
)+ m(
) +m(
) =m(
)+m(
)+m(
)= 180o .
Pe
de alta parte punctele D,E,F se unesc in punctul S (varful tetraedrului),
iar m(
)+m(
)+m(
)= 180o , ca fiind suma masurilor unghiurilor unui
triunghi.
T2 Evident , fig 1, caci AD si AF se vor identifica cu muchia [SD] opusa muchiei [BC], iar [BC]s[AD]s[AF]=a, la fel [DB] si [BE] vor da [SB]=b opusa lui [AC] =b si [EC], [cf] vor corespunde lui [SC]=c opusa lui [AB]=c.
T3 Muchiile opuse fiind congruente (fig 1) toate fetele vor fi triunghiuri congruente.
T1 Evident
T Sa presupunem ca paralelipipedul AFSGECDB este oblic (cu fetele paralelograme). Evident DBCEsDBCE. Daca ,de exemplu, fetele CFSD sau DSGB n-ar fi dreptunghiuri , atunci proiectiile ortogonale ale lui S si A pe planul de baza n-ar mai cadea in D si E,
iar D SCB s-ar proiecta , de exemplu intr-un
triunghi continand pe [BCD] , iar D ABC
intr-unul continut in DBCE sau
invers. Cum insa DBCD s DBCE , rezulta ca cele doua
triunghiuri mentionate mai sus si obtinute prin proiectie
ortogonala pe planul de baza nu vor fi egale
( decat in cazul in care toate fetele laterale ale
paralelipipedului vor fi dreptunghiuri).
Dar DSBC fiind echivalent cu DABC , iar baza
[BC] fiind comuna rezulta ca si inaltimea SH1=SH2.
Dar AS este paralela cu planul de baza asa ca
[SD]s[AE] si deci triunghiurile dreptunghice [SDH1] si
[AEH2] sunt congruente. Rezulta ca [DH1]s[EH2] , iar
din teorema celor trei perpendiculare deducem ca
DH1 BC, EH2 BC, adica sunt inaltimi in triunghiurile
[BCE] si[ BCD] , de unde conchidem ca cele doua triunghiuri sunt echivalente ,contrazicand constatarea facuta mai sus ca unul din ele ar fi continut intr-unul din triunghiurile in care diagonala [BC] descompune paralelogramul CEBD, iar celalalt triunghi l-ar contine pe cel ramas, contradictia obtinuta implica faptul ca fetele laterale ale paralelipipedului ( reprezentand in acelasi timp si proiectiile ortogonale ale tetraedrului pe planele respective) sunt dreptunghiuri. Pentru a demonstra si faptul ca si proiectia tetraedrului pe planul de baza , cat si pe cel paralel cu el sunt dreptunghiuri , n-avem decat sa consideram pentru moment ca planul de baza planul uneia din fetele laterale ale paralelipipedului si sa rationam ca mai sus.
T7 Din fig 3 , observam ca ABDF este un dreptunghi asa ca [AB]s[FD]; cum insa prin ipoteza CFSD este un dreptunghi el are diagonalele egale asa ca [CS]s[FD]s[AB], dar [SC] si [AB] sunt muchii opuse in tetraedrul [SABC].
La fel se arata si despre celelalte muchii opuse ca sunt congruente , ceea ce ne conchidem ca prin desfasurarea tetraedrului se obtine un triunghi ca in figura 1 in care [AB]; [BC]; [CA] sunt linii mijlocii.
Teorema 30:
Un tetraedru [ABCD] este echifacial daca si numai daca cele patru inaltimi ale sale sunt egale.
Demonstratie:
3V=hx Sx; dar SA=SB hA=hB e.t.c.
Teorema 31:
Tetraedrul [ABCD] este echifacial daca si numai daca au loc egalitatile cu unghiuri diedre:
A(BCD)=B(ADC)=C(DAB)=D(CBA).
Demonstratie:
Egalitatile (1) exprima ansamblul
urmatoarelor egalitati de unghiuri plane
ss
s
s
s
s
s
s
s
Daca au loc egalitatile (2) , unghiurile oricarui tetraedru sunt egale unghiurilor fetei "opuse" , deci insumeaza 180o si deci tetraedrul [ABCD] este echifacial. Daca [ABCD] este echifacial orice pereche de unghiuri de pe aceeasi linie din (2) sunt unghiuri congruente, intr-o congruenta de triunghiuri ce contine fete ale tetraedrului.
Teorema 32:
Un tetraedru este echifacial daca si numai daca centrele sferelor inscrise , respectiv circumscrise , coincid.
Demonstratie :
T Se foloseste teorema: Daca un tetraedru are toate fetele de aceeasi arie , atunci muchiile opuse sunt congruente si reciproc. Deci fetele tetraedrului sunt patru triunghiuri congruente, deci cercurile circumscrise lor au aceeasi raza R1.
Fie O centrul sferei circumscrise. Il proiectam pe O pe fiecare fata in punctele O1,O2,O3,O4. Se demonstreaza ca (OO1)s(OO2)s(OO3)s(OO4) adica O este si centrul sferei inscrise. Pentru aceasta este suficient sa se observe ca in punctele in acre se proiecteaza O sunt tocmai centrele cercurilor circumscrise fetelor ( de exemplu triunghiurile [OO1A], [OO1B], [OO1C] sunt congruente, deci (O1A)s (O1B)s (O1C).
Rezulta , folosind teorema lui Pitagora :
OO1=
. Analog se afla OO2, OO3, OO4,
R fiind raza sferei circumscrise tetraedrului).
Fie O centrul sferei circumscrise. O se proiecteaza pe fiecare
fata in centrul cercului circumscris acelei fete. Deci toate fetele admit
cercuri circumscrise de aceeasi raza
O1C=,OO1= r.
Rezulta,
de exemplu, 
ADBs ACB ( in cercuri egale la
coarde egale le corespund arce egale).
Analog
ssis. Deci suma unghiurilor
varfului D este de 180o. Analog si pentru celelalte varfuri.
Deci tetraedrul este echifacial.
Teorema 33:
a) Daca [ABCD] este un tetraedru echifacial, atunci planul bisector al oricarui diedru al sau este si planul median.
b) Daca pentru trei diedre ale tetraedrului [ABCD] avand muchiile
necoplanare planele bisectoare sunt si plane mediane , atunci tetraedrul
este echifacial.
Demonstratie:
a)
Daca planul bisector al diedrului 
taie in E muchia [CD],
conform teoremei
planului bisector 
dar SABC=SABD T (DE)s(EC). Deci E este mijlocul muchiei [CD].
b)
Fie ,
,
diedrele ale caror plane bisectoare
injumatatesc muchiile opuse [CD]; [AD];[AB]. Conform
primei parti au loc egalitatile SABC=SABD= SBCD=SACD si deci
tetraedrul [ABCD] este echifacial.
Observatie
In absenta precizarii de la punctul b) ca muchiile diedrelor nu sunt coplanare rezulta doar doua egalitati de arie de fete.
Lema 34:
Intr-un tetraedru
echifacial [ABCD], fiecare bimediana este perpendiculara comuna a
muchiilor ce le injumatatesc.
Demonstratie :
Fie M mijlocul lui [AB] si proiectiile ortogonale
E,F,N cele ale lui A,B,M pe muchia [CD].
Daca (AM)s(MB) rezulta (EN)s(FN).
Se observa ca AE CD=2SB=2SA=BF CD.
Deci (AE)s(BF) . Din triunghiurile dreptunghice
[AEN] si [BFN] rezulta (AN)s(NB). Deci in triunghiul
isoscel [NAB] mediana MN este si inaltime , prin urmare MN este perpendiculara comuna a muchiilor [AB], [CD]. Daca prin absurd N nu ar coincide cu mijlocul M al muchiei [CD] , s-ar relua constrictia si demonstratia schimband rolul muchiilor opuse [AB], [CD] si am gasi o alta perpendiculara comuna M N a muchiilor [AB],[CD], ceea ce este absurd.
|
Politica de confidentialitate |
 .com |
Copyright ©
2024 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |
