Fie E, E doua K - spatii euclidiene.
DEFINITIA 1. O transformare liniara F I L (E, E ) se numeste ortogonala daca pastreaza produsul scalar, adica
(F (![]() ),F (
),F (![]() )) = (
)) = (![]() ),
x,y I E.
),
x,y I E.
Notatie. Lort (E, E
Exemple. 1. Transformarea identica
I :
E
E este ortogonala
deoarece pentru orice ![]() I
E avem I (
I
E avem I (![]() ) =
) = ![]() si conditia (1) este deci indeplinita.
si conditia (1) este deci indeplinita.
2. Transformarea F : E
E care asociaza
fiecarui ![]() I E, opusul sau
I E, opusul sau
![]() , este ortogonala deoarece din relatia de definitie F (
, este ortogonala deoarece din relatia de definitie F (![]() ) =
) = ![]() pentru orice
pentru orice ![]() I E, rezulta conditia (1).
I E, rezulta conditia (1).
TEOREMA 1. Conditia necesara si suficienta ca o transformare liniara F IL (E, E ) sa fie ortogonala este ca ea sa pastreze lungimea vectorilor, adica
|| F (![]() ) || = ||
) || = ||![]() ||,
||,
![]() I E.
I E.
Demonstratie.
Daca
F I Lort (E,
E ) atunci (F (![]() ),F (
),F (![]() ))=(
))=(![]() ) (conform cu (1)),din care rezulta || F (
) (conform cu (1)),din care rezulta || F (![]() ) || = ||
) || = ||![]() ||,
||, ![]() I E.
I E.
Reciproc, daca || F(![]() ) || = ||
) || = ||![]() ||,
||,
![]() I E, consideram
I E, consideram
![]() F
F ![]() F
F ![]()
![]() F
F ![]() F
F ![]() F
F ![]() F
F ![]() F
F ![]() (( F
(( F ![]() F
F ![]() )2 - -F
)2 - -F ![]() F
F ![]() ( F
( F ![]() F
F ![]() ).
).
Consecinta 1. Orice transformare ortogonala este injectiva.
Intradevar,
daca
F I L (E, E ),
din F (![]() ) = 0E rezulta, conform cu relatia
(2), ca
) = 0E rezulta, conform cu relatia
(2), ca
||![]() || = || F (
|| = || F (![]() ) || = || 0E ||
= 0, adica Ker (F ) = , adica
F injectiva (cf.T.1.3.6).
) || = || 0E ||
= 0, adica Ker (F ) = , adica
F injectiva (cf.T.1.3.6).
TEOREMA 1. (1) Produsul a doua transformari ortogonale este tot o transformare ortogonala.
Inversa unei transformari ortogonale surjective este tot o transformare ortogonala.
Demonstratie. (1) Fie F :
E
E
si
F :
E
E
doua
transformari
ortogonale si F F F :
E
E
produsul lor. Dupa
proprietatea1.3.3.1, F este liniara
si
tinand seama de relatia (2), avem || F (![]() ) || = || F F (
) || = || F F (![]() )) || = || F (
)) || = || F (![]() ) || = ||
) || = ||![]() ||,
||,
![]() I E deci F este ortogonala.
I E deci F este ortogonala.
Fie F ILort(E, E ), F surjectiva , atunci F este bijectiva si deci exista F : E E care este, conform proprietatii 1.3.3.5, transformare liniara. Punand F (v') = v sau echivalent v F (v) si tinand seama de (2) obtinem || F (v ) || = || v || = || F (v) || = || v v I E adica F este ortogonala.
Din Teorema 1.5.2. rezulta
Consecinta 1. Operatia de compunere determina pe multimea endomorfismelor ortogonale surjective ale unui spatiu vectorial euclidian E pe el insusi o structura de grup.
Acest grup se numeste grupul ortogonal al spatiului euclidian E si-l vom nota G O (E). El este subgrup al grupului liniar G L (E) - grupul format de multimea endomorfismelor lui E.
TEOREMA 1.5.3. Conditia necesara si suficienta ca F I Lort (E, E ) este ca matricea M(F ; B,B ) a transformarii F in raport cu orice baze ortonormate B si B din E, respectiv, E sa verifice egalitatea
Mt(F ; B,B M(F ; B,B ) = In ,
unde In este matricea unitate de ordinul n = dimE.
Demonstratie. Presupunem ca F ILort(E, E )
atunci ![]() I E, || F (
I E, || F (![]() ) || = ||
) || = ||![]() ||, rezulta (F (
||, rezulta (F (![]() ),F (
),F (![]() ))=(
))=(![]() ) atunci [F (
) atunci [F (![]() )]tB
F (
)]tB
F (![]() )]B =[
)]B =[![]() ]tB[
]tB[![]() ]B si, cum [F (
]B si, cum [F (![]() )]B = M(F ; B,B )[
)]B = M(F ; B,B )[![]() ]B ,rezulta [
]B ,rezulta [![]() ]tB
Mt(F ; B,B
M(F ; B,B
[
]tB
Mt(F ; B,B
M(F ; B,B
[![]() ]B = [
]B = [![]() ]tB
In [
]tB
In [![]() ]B , de unde rezulta (3).
]B , de unde rezulta (3).
Reciproc,
presupunem adevarata
relatia
(3) si
parcurgand
in
sens invers demonstratia precedenta rezulta || F (![]() ) || = ||
) || = ||![]() ||, adica F I Lort (E, E
||, adica F I Lort (E, E
DEFINITIA 1. Matricea patrata A I M (n, n, R) se numeste ortogonala daca satisface relatia
(4) A At = At A = In .
Consecinte 1.5.3. (1) Daca F ILort(E, E) atunci M(F ; B) este matrice ortogonala.
Daca A este matrice ortogonala, atunci det A =
Daca A si B sunt doua matrice ortogonale, atunci si matricea A B este o matrice ortogonala.
Inversa unei matrice ortogonale este o matrice ortogonala.
Daca A si
B sunt matrice ortogonale, atunci si matricea ![]() este ortogonala.
este ortogonala.
Demonstratie. (1) este evidenta.
Tinand seama de proprietatea ca det (A B) = det (A) det (B), avem din relatia (4)
det (A At) = det In T detA det At = 1
si, cum det A = det At, rezulta (det A)2 = 1 T det A =
Din ipoteza A At = In, B Bt = In , rezulta
(AB) (AB)t = (AB) (BtAt)= A (BBt) At = A In At = AAt = In .
Fie B = A-1 si AAt = In. Avem succesiv
B Bt = (A-1) (A-1)t = A-1 (At)-1 = (A At)-1 = In-1 = In.
Tinand seama de (3), avem pe rand
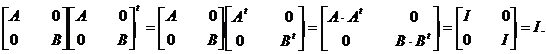
Observatie 1. In C.1.5.3.(5) nu este necesar ca cele doua matrice sa fie de acelasi ordin.
DEFINITIA 1. Un endomorfism ortogonal F se numeste rotatie daca
detM(F ; B)= 1, unde M(F ; B) este matricea lui F asociata bazei B a spatiului vectorial.
|
Politica de confidentialitate |
| Copyright ©
2024 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |