
Varianta (fluctuatia) dispersa sau abaterea medie patratica . Notiunea de momente
O alta caracteristica cantitativa a variabilei aleatoare x, care difera de valoarea medie care determina pozitia centrului de distributie a probabilitatilor, este varianta sau dispersia variabilei aleatoare.
Vom nota varianta prin D Varianta este caracteristica numerica a imprastierii, deviatia valorilor variabilelor aleatoare in raport cu valoarea medie a acestei variabile.
Definitia 1: Se numeste varianta variabilei aleatoare X speranta matematica a patratului diferentei dintre variabila aleatoare X si speranta sa matematica (altfel spus speranta matematica a patratului variabilei aleatoare centrata corespunzatoare.)
D[x] = M[(x-mx)2]
sau
![]()
![]() D[x] =
D[x] = ![]()
Varianta nu poseda aceeasi unitate de masura ca si variabila aleatoare . Uneori este comod pentru a caracteriza dispersia valorilor, de a utiliza o marime a carei unitate de masura coincide cu cea a variabilei aleatoare, pe care o numim abatere medie patratica .
Definitia 2: Se numeste abatere standard a variabilei aleatoare, radacina patrata a variantei.
G[x] = ![]()
sau sub o forma mai explicita
G[x]
= 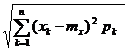
Aleatoarea standard este uneori notata si cu
Remarca 1: Pentru calcule este comod sa se transforme formula (VII 40) dupa cum urmeaza:
D[x] = ![]()
![]() =
=
= ![]() - 2
- 2![]()
![]() +
+ ![]() =
=
M[![]() ] - 2
] - 2![]() +
+ ![]() =
=
M[![]() ] -
] - ![]()
Astfel
D[x] = M[x2] - ![]()
Altfel spus varianta este egala cu diferenta sperantei matematice a patratului variabilei aleatoare si patratul sperantei matematice a variabilei aleatoare.
Exemplul 1. Se efectueaza o experienta in cursul careia evenimentul A poate sa se produca sau nu. Probabilitatea de realizare a evenimentului A este egala cu p. Sa se determine speranta matematica, varianta si abaterea patratica medie.
Solutie:
Asezam intr-un tablou valorile numarului de realizare a evenimentului (q = 1-p):
|
x | ||
|
pk |
p |
q |
in consecinta:
M[x] = 1* p + 0 * q = p
D[x] = (1- p + (0 - p)2 q = q * p
G[x] = ![]()
Pentru a elucida sensul notiunilor variantei si abaterii patratice medii precum si caracteristicile dispersiei variabilei aleatoare consideram cateva exemple:
![]()
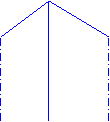 P
PFig 3
0 0,4 0,3
![]()
0 2 3 4
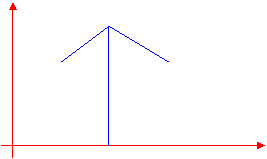
![]()
![]()
0 Fig 4
0 1 2 3 4 5
Exemplul 2: Variabila aleatoare x data de legea de distributie urmatoare (vezi Fig. 3)
|
x |
|
||
|
pk |
Sa se determine:
M[x] = 2 * 0,3 + 3 * 0,4 + 4 * 0,3 = 3
D[x] = (2-3)2 * 0,3 + (3-3)2 * 0,4 + (4-3)2 * 0,3 = 0,6
G[x] = ![]() =
= ![]() = 0,77
= 0,77
Exemplul 3. Variabila aleatoare x este data de legea de distributie urmatoare (Fig. 4)
|
x | |||
|
pk |
Sa se determine:
Speranta matematica
Varianta
Abaterea patratica medie
Solutie
M[x] = 1 * 0,3 + 3 * 0,4 + 5 * 0,3 = 3
D[x] = (1-3)2 * 0,3 + (3-3)2 * 0,4 + (5-3)2 * 0,3 = 2,6
G[x] = ![]() = 1,55
= 1,55
Dispersia, deviatia variabilei aleatoare, este in exemplul 2 inferioara dispersiei variabilei aleatoare din cel de al doilea exemplu. Variabilele (fluctuatiile) acestor marimi sunt respectiv egale cu 0 si 2,4.
Exemplul 4. Variabila aleatoare este data de legea de distributie urmatoare:

P
|
x | |
|
p |
![]()
0 3
Sa se determine:
Solutie:
M[x] = 3 * 1 = 3
D[x] = (3-3)2 * 1 = 0
G[x] = 0
dispersia acestei variabile aleatoare este nula.
Remarca 2. Daca
consideram o cantitate
Demonstratie. Am aratat deja ca M(c)= c. Cu ajutorul formulei (VII 40) avem:
D[c] = M [(c-c ] = M[0] = 0
Remarca 3. Prin analogie cu terminologia utilizata in mecanica se numesc momente centrale de primul sau al doilea ordin al variabilei aleatoare x speranta matematica a cantitatilor (x- mx); (x- mx)2. Se considera de asemenea momentul centrat de ordinul trei:
![]()
Daca variabila aleatoare este distribuita simetric in raport cu centrul distributiei probabilitatilor (Fig 1), este evident ca momentul sau central de ordinul 3 va fi nul. Daca momentul central de ordinul trei este nul, variabila aleatoare nu poseda o distributie simetrica.
|
Politica de confidentialitate |
| Copyright ©
2024 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |