
Raporturile deductive dintre propozitii pot fi studiate abstractie facandu-se de forma concreta a propozitiilor respective. De pilda, din adevarul propozitiei P putem deduce adevarul lui P Q, indiferent de forma logica pe care o au propozitiile P si Q. Am numit aceste propozitii simple sau atomare.
Printre propozitiile simple gasim insa unele care prezinta o importanta logica aparte. Este vorba de propozitiile de tip "S este P" numite si "propozitii de predicatie". Intrucat sunt propozitii care genereaza un tip specific de inferenta va trebui sa le discutam separat.
Denumirea de "propozitie de predicatie" provine din faptul ca aici se predica ceva despre altceva. Am vazut in capitolul anterior ca predicatia este o operatie logic originara, ea nu poate fi redusa la alte operatii.
Denumirea de "propozitie categorica" indica altceva, ea subliniaza raporturile dintre clasele (categoriile) ce alcatuiesc subiectul, respectiv, predicatul logic al acestor propozitii.
In fine, Leibniz a impus denumirea de "propozitie de inerenta" de la formula sa predicatum inest subjecto. Multi insa le numesc "propozitii aristotelice" datorita pozitiei privilegiate pe care o detin ele in logica lui Aristotel
Distingem in raport cu propozitiile de predicatie cateva elemente structurale, si anume:
1. Subiectul propozitiei. Este notiunea corespunzatoare obiectelor despre care se afirma sau se neaga ceva in propozitie. Cand spunem "Unii tineri nu sunt seriosi", subiectul logic este notiunea tanar. (subiectul logic coincide aici cu cel gramatical).
In multe manuale se spune ca subiectul logic este notiunea despre care se afirma sau se neaga ceva in propozitie. Formularea este gresita din simplul motiv ca in propozitia "Omul este rational" sau "Toti oamenii sunt fiinte rationale" noi nu despre notiunea om vrem sa spunem ca este rationala, ci despre ceea ce cade in sfera acestei notiuni. Or, nu este acelasi lucru a vorbi despre notiune sau a vorbi despre obiectele la care se aplica notiunea.
2. Predicatul propozitiei. Este notiunea corespunzatoare insusirii afirmate sau negate in propozitie despre obiectele din sfera subiectului. In exemplele de mai sus, predicat este notiunea serios, respectiv rational.
Uneori predicatul logic se aplica in general la obiectele din sfera subiectului, ca in exemplul "Trapezul este patrulater". Acestea propozitii indica un alt element din structura propozitiei de predicatie, si anume, obiectul propozitiei.
Ce este acest obiect?
Este obiectul notiunii subiect, el reprezinta "suportul" afirmatiilor, respectiv, negatiilor noastre in propozitie. Am vorbit cu alte ocazie despre aceste lucruri asa ca nu insist mai mult asupra lor.
Subiectul si predicatul logic notate, de obicei, cu literele S, P se numesc termenii propozitiei.
3. Copula. Acea parte a propozitiei exprimata printr-un mod al verbului "a fi" cu ajutorul careia se realizeaza predicatia se numeste copula. De obicei, rolul de copula il are cuvantul "este", respectiv, "sunt".
Pe langa predicatie, cuvantul "este" indeplineste o serie de alte functii:
1) identitatea. Aceasta poate fi simpla sau definitionala (a = a, respectiv, a =df b),
2) incluziunea A B (citeste "A este inclus in B")
3) relatia : "a este in relatia R cu b".
4) existenta (in genere, sau existenta determinata): a este in cutare fel sau, pur si simplu, a este (se pare ca Abelard este cel care a deschis discutia in logica medievala despre functiile cuvantului "este" in propozitie).
4. Cuantorii. De cele mai multe ori notiunea subiect este afectata in propozitie de expresii cum ar fi "toti", "unii", "nici unul" s.a. Ele indica faptul ca sfera subiectului este luata in totalitate sau numai dupa o parte a ei. Asa cum am mai spus, aceste expresii se numesc "cuantori" si dau ceea ce se cheama cantitatea propozitiei.
Propozitiile au calitatea de-a fi afirmative sau negative. Cele negative se formeaza cu ajutorul negatiei, operatie ce poate afecta propozitia ca intreg sau numai copula.
Propozitiile:
"Nu este adevarat ca toti oamenii sunt coruptibili",
"Nu toti oamenii sunt coruptibili",
"Nici un om nu este coruptibil",
"Unii oameni nu sunt coruptibili"
sunt, toate, propozitii negative.
In primele doua negatia afecteaza propozitia ca intreg, ele au forma "Nu este adevarat P", respectiv, "Nu P". In cel de-al treilea exemplu negatia afecteaza atat propozitia cat si copula, iar in ultimul exemplu negatia afecteaza doar copula. In toate cazurile avem de-a face cu propozitii negative.
S-ar putea intampla ca negatia sa afecteze doar termenii propozitiei (subiectul, respectiv, predicatul) insa atunci propozitia nu isi schimba calitatea. De pilda, "Unii oameni sunt needucabili" sau "Orice nonmamifer este neerbivor" sunt afirmative cu toate ca subiectul si/sau predicatul lor sunt termeni negativi.
Cuantorii "toti", "unii", "nici unul", "fiecare" s. a. indica faptul ca proprietatea exprimata prin predicat este afirmata, respectiv negata, despre
● toate obiectele din sfera predicatului,
● numai despre unele,
● despre unul singur,
● despre nici unul.
Propozitiile din prima si ultima categorie se numesc universale. Cuantorul universal se exprima prin cuvintele "toti", "oricare", "fiecare", "nici unul":
"Toti sportivii sunt oameni",
"Orice masina are o marca",
"Fiecare om poarta un nume",
"Nici un om nu este nemuritor".
Desi "toti" si "fiecare" se presupun reciproc, intre aceste cuvinte exista totusi o diferenta. In cazul lui "toti", obiectele sunt vizate simultan, sunt luate toate deodata, fata de "fiecare" unde obiectele sunt vizate unul cate unul.
Expresia "oricare" aduce o alta nuanta, aici universalitatea presupune operatia de alegere aleatoare. Sensul expresiei este urmatorul: putem alege la intamplare un element dintr-o clasa si acel element are o anume proprietate intrucat toate elementele clasei au acea proprietate.
In fine, "nici unul" este cuantorul universal adaptat propozitiilor negative. Cand spunem "Nici un om nu este vesnic" intelegem ca proprietatea de-a fi vesnic este exclusa fata de clasa oamenilor in totalitatea ei. Prin urmare, cuantorul este universal.
De ce este important sa aducem in discutie aceste probleme?
Bertrand Russell a semnalat asa numitele "totalitati ilegitime" generate de utilizarea abuziva a cuvantului "toti". De exemplu, expresia "toate clasele" lasa sa se inteleaga ca ar fi vorba de o noua clasa - clasa tuturor claselor - astfel ca ceea ce este valabil pentru fiecare clasa in parte este valabil si pentru noua clasa. De aici o noua forma de cerc vicios prezent, practic, in toate paradoxurile in care intervine ideea de clasa. Russell a incercat sa elimine aceste totalitati ilegitime prin ierarhiile lui de tip si ordin.
Propozitiile in care se afirma sau se neaga ceva numai despre unele obiecte din sfera subiectului se numesc particulare.
"Unii studenti sunt bursieri",
"Unele numere nu sunt pare",
"Unii oameni nu disting rosul de verde" etc.
Exista si aici cateva nuante datorate faptului ca expresia "unii" (cuantificatorul particular) poate fi luata in diferite sensuri. Iata cateva dintre cele mai importante:
1) Sens neexclusiv in care "unii" inseamna "cel putin unul, nu este exclus toti". Cand spunem "Unii elevi sunt vaccinati" intelegem ca exista un numar oarecare de elevi despre care stim sigur ca sunt vaccinati, dar nu este exclus sa fie toti vaccinati. In acelasi fel intelegem propozitia "Unii studenti sunt bursieri" sau "Unii parlamentari sunt corupti".
2) Sens exclusiv. Desi propozitia "Unele pasari sunt infestate" are aceeasi forma cu propozitia "Unele numere sunt pare" intre ele exista o mare diferenta. Nu putem spune ca unele numere sunt pare dar ca n-ar fi exclus ca toate numerele sa fie pare asa cum am spune ca unele pasari sunt infestate dar n-ar fi exclus ca toate sa fie infestate. In propozitia noastra "unii" are sens exclusiv, el inseamna "unii, exclus toti".
2) Sens exclusiv nuantat. De multe ori "unii" inseamna "unii si numai unii" ca in propozitia "Unii romani sunt miliardari".
Sa recapitulam.
Primul sens al lui "unii" este nedeterminat in cel mai inalt grad. Spunand "Unele mari sunt poluate" noi nu stim nici despre care mari este vorba si nici cate sunt ele.
Al doilea sens restrange intrucatva nedeterminarea prin faptul ca il exclude pe "toti".
Al treilea aduce o nuanta in plus localizand oarecum obiectele din sfera subiectului. Spunand "Unii si numai unii merg peste hotare" stim din capul locului ca nu este vorba despre toti, ci despre cativa pe care, de regula, ii si putem indica. In acelasi fel poate fi "tradusa" propozitia "Unii profesori se bucura de aprecierea studentilor".
Cele doua criterii, calitatea si cantitatea, se pot combina astfel ca vor rezulta patru clase de propozitii, asa cum se vede din figura de mai jos:
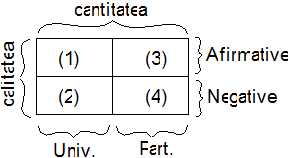
Clasa (1) contine propozitiile universal afirmative (Toti S sunt P); clasa (2) contine propozitiile universal negative (Nici un S nu este P); a treia clasa contine propozitiile particular afirmative (Unii S sunt P), iar ultima clasa contine propozitiile particular negative (Unii S nu sunt P).
Pentru a putea opera mai usor cu aceste forme propozitionale, medievalii au introdus simbolurile a, e, i, o, care provin din cuvintele latinesti affirmo (a afirma) si nego (a nega). Primele doua vocale din affirmo, respectiv a si i, desemneaza propozitiile afirmative, iar cele doua vocale din nego (e si o) desemneaza propozitiile negative. Expresiile SaP, SeP, SiP si SoP corespund celor patru propozitii de predicatie, dupa cum urmeaza:
SaP = Toti S sunt P, SeP = Nici un S nu este P,
SiP = Unii S sunt P, SoP = Unii S nu sunt P.
Aceleasi propozitii se exprima in limbajul Lukasiewicz prin Asp, Esp, Isp si Osp. Simbolurile a, e, i o (respectiv, A, E, I, O) semnifica, fie tipul propozitiei (universal afirmativa, universal negativa etc.), fie relatia dintre termenii propozitiei. De exemplu, a (sau A) este relatia "Toti. sunt."; i (sau I) este relatia "Unii. sunt." si asa mai departe.
3. PROPOZITIILE SINGULARE
Propozitiile in care se afirma sau se neaga ceva despre un singur obiect se numesc propozitii singulare. "Socrate este om", "4 este numar par", "Eminescu este roman" sunt, toate, propozitii singulare.
In ciuda simplitatii lor, statutul acestor propozitii este inca departe de-a fi clarificat. Unii le trateaza dupa modelul propozitiilor universale argumentand ca subiectul acestor propozitii este o clasa cu un singur element pe care predicatul o vizeaza in totalitate. Argumentul nu mi se pare convingator in primul rand pentru ca intre element si clasa care contine acel element diferenta este esentiala. Apoi, propozitiile singulare nu pot fi cuantificate.
In cele ce urmeaza voi incerca sa ma opresc asupra unor probleme mai speciale pe care le ridica propozitiile singulare.
Prima este asa numita teza lui P. T. Geach, cunoscuta si ca teza asimetriei dintre subiect si predicat cu privire la negatie (sau, mai simplu, teza asimetriei). Este vorba de faptul ca in propozitiile singulare, spre deosebire de propozitiile generale, numai predicatul lor poate fi negat, nu si subiectul. De exemplu, din propozitia "Socrate este filosof" putem forma propozitia "Socrate este non-filosof" (sau "nefilosof)". Propozitia este, evident, falsa dar ea este tot o propozitie singulara, vreau sa spun o propozitie singulara corecta pentru ca propozitia "Non-Socrate este filosof" (sau "nefilosof") nu este o propozitie corecta.
Strawson a aratat ca teza asimetriei este valabila nu doar in cazul negatiei, ci si al altor operatii cum ar fi operatia de compunere a predicatelor. De pilda, din propozitiile "a este A" si "a este B" putem forma o propozitie cu un predicat compus: "a este AB".
Nu acelasi lucru se intampla in cazul subiectului. Daca "a este A" si "b este A" nu putem forma propozitia "ab este A". Subiectele "Socrate" si "Platon" nu se pot combina in subiectul compus "Socrate Platon" asa cum se combina "filosof" si "grec" in predicatul "filosof grec". Este, cum am mai spus, prima caracteristica a propozitiilor singulare si, totodata, prima deosebire fata de restul propozitiilor.
O alta deosebire este data de functia referentiala a subiectului in propozitie. Cand spunem "Socrate este filosof" subiectul "Socrate" se refera (denota) un individ anume despre care se predica insusirea exprimata prin predicat. Acelasi lucru se intampla in cazul propozitiei universale "Toti A sunt B". Si aici A se refera (sau denota) anumiti indivizi despre care se predica insusirea exprimata prin B. Stim, insa, ca unele propozitii universale se convertesc simplu, din "Toti A sunt B" se obtine "Toti B sunt A", in care functiile s-au inversat (la obiectele denotate de B se aplica insusirea exprimata prin A). In fine, in propozitiile de identitate "Toti A sunt A", acelasi termen A denota anumiti indivizi (in calitatea lui de subiect) si exprima anumite insusiri (in calitatea lui de predicat).
Dar atunci care mai este semnificatia termenilor in propozitiile de predicatie? Obiectul, respectiv, clasa de obiecte? Insusirea? Sau obiectul plus insusirea?
Trebuie cumva sa admitem, cum face Quine, ca nu exista referent in genere, ca referentul unui termen depinde exclusiv de functia pe care o indeplineste termenul in propozitie?
Orice raspuns am da, este de subliniat ca o asemenea ambiguitate nu apare in cazul propozitiilor singulare, subiectul acestor propozitii, spre deosebire de predicatul lor, nu poate exprima niciodata o insusire. Deci teza asimetriei se mentine si in acest caz.
Dupa parerea mea, exista si o a treia caracteristica a propozitiilor singulare, o caracteristica ce consta in functia lor predicativa, in faptul ca doar in aceste propozitii se realizeaza operatia de predicatie. Pentru ca problema este ceva mai complicata voi incepe prin a reaminti cateva chestiuni din logica conceptului.
Am vazut in capitolul anterior ca propozitia singulara "a este A" exprima relatia de cadere a obiectului sub concept, sau, ceea ce este acelasi lucru, predicarea conceptului despre obiect.
Totalitatea obiectelor despre care se predica conceptul A formeaza sfera sau extensiunea conceptului A. In figura (2) este redata sfera conceptului A in timp ce figura (1) reda aplicarea acestui concept la unul din obiectele sferei sale. Practic, figura (1) este o sectiune a figurii (2):
A A
![]()

n n n n n nnnnnn n
ai a1, a2, ........, an
fig.(1) fig.(2)
Asa numitele propozitii de predicatie (AaB, AiB etc) nu realizeaza predicatia in mod propriu, ele isi "datoreaza" predicativitatea propozitiilor singulare. Vreau sa spun ca numai in propozitia singulara se predica ceva despre altceva, celelalte propozitii sunt numite "de predicatie" doar pentru faptul de-a contine propozitia singulara.
De pilda, in propozitia universal afirmativa "Toti A sunt B" predicatia se realizeaza conform schemei:
B B
![]()

A
 A
A
![]()
n n n n n n n n n n n n
ai a1, a2, .......... , an
fig. 3. fig. 4.
A(ai) B(ai) (1)
(x) A(x) B(x) (2)
Propozitia universal negativa "Nici un A nu este B" este cea mai simpla din punct de vedere al predicatiei:
A B


nnnnnnnnn nnnnnnnnn
fig.
In forma simbolica:
(x) A(x) ![]() (3)
(3)
Citeste: oricare ar fi x, daca x este A, atunci x nu este B (sau este non-B). Propozitia spune ca intre predicatiile realizate de cele doua concepte A si B nu exista nici un fel de implicatie.
In fine, particulara afirmativa "Unii A sunt B" si particulara negativa, "Unii A nu sunt B" realizeaza predicatia conform figurii 6 (A se predica despre unele obiecte din sfera lui B, respectiv, A se predica despre unele obiecte care nu cad in sfera lui B ):
A B


n n n n n n n n n n
Cele doua propozitii se reprezinta simbolic prin:
x A(x) & B(x) (4)
x A(x)
& ![]() (5)
(5)
care inseamna: exista x (x insemnand obiecte) despre care se predica atat A cat si B (reformulat: "exista x astfel ca x este A si x este B). Formula (5) corespunde particularei negative si se citeste: "exista x astfel ca x este A, dar nu B".
Prin urmare, toate cele patru propozitii de predicatie contin propozitii singulare intr-o anumita organizare logica, propozitii corelate cu ajutorul unor binecunoscute operatii si relatii logice. Parerea mea este ca desi sunt numite "de predicatie", ele isi datoreaza predicativitatea exclusiv propozitiilor singulare.
Dar nu numai propozitiile categorice presupun propozitiile singulare, ci si alte genuri de propozitii, cum ar fi propozitiile de relatie. Propozitia "a > b" (a este mai mare decat b) poate fi inteleasa ca propozitie singulara in trei moduri diferite:
1) a este numar mai mic decat b (obiectul a cade sub conceptul numar mai mic decat b). Propozitia nu mai este de forma xRy ci de forma A(x).
2) b este numar fata de care a este un numar mai mic. Aici b este obiect fata de conceptul numar fata de care a este numar mai mic. Propozitia are, din nou, forma A(x).
>(a, b). Conceptul, de data aceasta, este mai mare, iar obiectul este perechea ordonata (a, b). Propozitia este de forma R(x, y), notatia obisnuita a unei relatii binare.
Cu aceasta consider problema propozitiilor singulare suficient lamurita. Redau in incheiere interpretarile celor patru propozitii de predicatie:
![]()
![]()
![]()
AaB = Toti A sunt B = (x) A(x) B(x) = Oricare ar fi x, daca x este A, x este B,
AeB = Nici un A nu este B = (x) A(x) ![]() = Oricare ar fi x, daca x este A, x nu este B
= Oricare ar fi x, daca x este A, x nu este B
AiB = Unii A sunt B = x A(x) & B(x) = Exista x astfel ca x este A si x este B
AoB = Unii A nu sunt B = x A(x) & ![]() = Exista x astfel ca x este A dar nu este B
= Exista x astfel ca x este A dar nu este B
O propozitie oarecare se zice ca este in forma standard daca poate fi obtinuta dintr-una din formele "Toti S sunt P", "Unii S sunt P" etc. prin substitutii corespunzatoare ale variabilelor S si P.
Operatia de aducere a propozitiilor la forma standard se numeste, la randul ei, standardizare. Propozitia "Unele pasari migreaza", de exemplu, se standardizeaza prin "Unele pasari sunt migratoare". In acest caz, S = pasare si P = migrator, deci propozitia este de forma "Unii S sunt P".
Pentru a determina raporturile formale ale propozitiilor, inclusiv raporturile lor inferentiale, este important sa stim cand si in ce conditii o propozitie poate fi adusa la forma standard. Pe de alta parte, validitatea inferentelor poate fi cel mai corect apreciata cand premisele si concluziile lor sunt propozitii in forma standard.
Pentru ca nu exista reguli universal valabile de standardizare, va trebui sa ne multumim cu cateva cazuri particulare.
1) Propozitii in cuantificare nonstandard. Cei doi cuantori, universal si particular, sunt de baza in logica insa cantitatea propozitiilor se mai poate exprima uneori si prin alt fel de cuantori. Nu intotdeauna acesti cuantori pot fi redusi la cuantorii de baza fara ca sensul propozitiilor sa nu fie serios afectat. De pilda, propozitia "Majoritatea oamenilor sunt angajati" spune ceva mai mult decat simplul fapt ca unii oameni sunt angajati.
Astfel de cuantori cum ar fi: "majoritatea", "anumiti", "multi", "destui" s.a. se numesc nonstandard, ei implica cuantorul particular "unii" fara sa se reduca insa la acesta. Deci propozitiile in cauza nu pot fi standardizate.
Curioase sunt si combinatiile: "destul de multi", "exista cativa", "numai o parte" care vizeaza, de asemenea, cantitatea propozitiilor.
Propozitiile universale, ca si cele particulare, pot fi redate uneori cu ajutorul unor expresii temporale: intotdeauna, ori de cate ori, niciodata, din cand in cand s.a.
Propozitia "Intotdeauna razboaiele produc tragedii" se standardizeaza prin "Toate razboaiele.". Aceasta pentru ca expresiile "toti", "toate" se pot referi nu doar la lucrurile care exista, ci si la cele care au existat sau vor exista in viitor. Chiar si in propozitia "Toti oamenii sunt muritori" noi nu ne referim doar la oamenii care exista in momentul de fata, ci si la oamenii care au existat sau vor exista candva.
2) Propozitii exceptive. Adeseori intalnim propozitii de forma "Toti S, cu exceptia lui X, sunt P": "Toate metalele cu exceptia mercurului sunt solide", "Toate capitalele, cu exceptia Bucurestiului, sunt murdare". Aceste propozitii se numesc exceptive.
Exceptia poate fi o clasa de indivizi sau doar un singur individ. Ea poate viza o lege, o norma sau numai o conventie. De exemplu, "Toate masinile cu exceptia salvarii trebuie sa opreasca la culoarea rosie a semaforului" este o exceptie in raport cu norma. Propozitia "Toate metalele cu exceptia mercurului sunt solide" este un alt caz de exceptie - exceptie in raport cu legea.
Standardizarea acestor propozitii se face, fie prin conjunctia a doua propozitii universale (una afirmativa, alta negativa), fie prin conjunctia unei universale cu o propozitie singulara.
Se spune: "Toate metalele sunt solide, dar mercurul este lichid"; "Toti profesorii sunt reciclati, dar niciun profesor de matematica nu este reciclat"; "Toate pasarile zboara, dar pinguinii nu zboara" etc. In aceste propozitii "dar" este o conjunctie, el inseamna "si".
3) Propozitii exclusive. Cand vrem sa accentuam faptul ca predicatul se atribuie in exclusivitate obiectelor din sfera subiectului folosim propozitii exclusive de genul "Numai cei care sunt S sunt P": "Numai laureatii la olimpiadele scolare sunt scutiti de admitere", "Numai romanii sunt geniali".
Si in acest caz folosim o conjunctie de doua universale: "Toti laureatii sunt scutiti de admitere si nici un nelaureat nu este scutit".
Cuvantul "doar" indica un alt gen de exclusivitate. Cand spunem "Presedintele a invitat doar membrii partidului sau" intelegem "Toti invitatii presedintelui sunt membrii ai partidului sau si niciun nemembru al partidului sau nu este invitat". Exclusivitatea in astfel de cazuri se reda prin conjuctia dintre o universala afirmativa si o universala negativa.
4) Propozitii implicative. Daca antecedentul si consecventul unei implicatii vorbesc despre aceleasi lucruri, propozitiile implicative se standardizeaza ca propozitii universale. Propozitia "Daca un animal are coada, atunci el nu este urs" se traduce prin "Nici un urs nu are coada" (sau "nu este animal cu coada").
Alte cazuri de standardizare se refera la verbul propozitiilor. Unele din aceste verbe se pot inlocui cu "este", respectiv "sunt", desi, cum am vazut, nu orice propozitie care contine aceste verbe este neaparat o propozitie de predicatie. Este important sa notam, totusi, ca de multe ori legatura dintre subiect si predicat se realizeaza printr-un mod al verbului "a avea". Propozitia "Toate girafele au gatul lung" poate fi luata ca o propozitie de predicatie: "Toate girafele sunt animale cu gatul lung". Asa cum am spus, este greu sa facem un inventar complet al tuturor formelor de standardizare.
Am spus in Introducere ca diagramele sunt figuri (scheme) grafice cu ajutorul carora se reprezinta raporturile dintre propozitii sau raporturile dintre termeni in cadrul aceleiasi propozitii. Exista mai multe tipuri de diagrame insa numai doua vor fi folosite in aceasta carte.
Diagrame Euler. Extensiunea subiectului si a predicatului pot fi redate sub forma unor cercuri, astfel ca raportul acestor cercuri reprezinta raportul celor doi termeni in structura propozitiei de predicatie. De exemplu, diagramele de mai jos corespund propozitiei universal afirmative.
|
|
|
In primul caz subiectul este coextensiv predicatului, ca in propozitia "Toti oamenii sunt fiinte rationale". In al doilea caz, sfera subiectului este inclusa in sfera predicatului (ex. "Toate cartile sunt publicatii"). Ambele propozitii sunt de forma "Toti S sunt P".
Propozitia universal negativa "Nici un S nu este P" se reprezinta prin diagrama:
|
|
|
Aici subiectul si predicatul nu au nici un element comun (de ex. "Nici un patrat nu este trapez").
Particulara afirmativa se reda prin:
|
|
in care partea hasurata corespunde acelor lucruri care sunt atat S cat si P, ca in exemplul "Unii poeti sunt filosofi".
In fine, particulara negativa are diagrama
|
|
unde partea hasurata corespunde acelor lucruri care sunt S fara sa fie P.
In cartea sa, Silogistica judecatilor de predicatie, Florea Tutugan a atras atentia asupra faptului ca diagramele Euler nu pot reda complexitatea raporturilor dintre termenii propozitiilor, ca in aceste diagrame propozitiile sunt reduse exclusiv la raporturile de extensiune ale termenilor (de aici o serie de limite in abordarea silogisticii).
Diagrame Venn. In aceste diagrame termenii sunt
reprezentati tot prin clase, dar, spre deosebire de diagramele Euler, aici
clasele sunt raportate la un univers de discurs (in diagrama universul de
discurs este reprezentat prin chiar spatiul dreptunghiului). Raportat la
universul de discurs, fiecare termen va determina o clasa si
complementara ei. Complementara clasei A,
notata ![]() , inseamna clasa
acelor lucruri care nu apartin lui A.
, inseamna clasa
acelor lucruri care nu apartin lui A.

Daca notam cu 1 universul de discurs,
complementara lui A se poate defini
prin 1- A. Intre A si ![]() au loc relatiile:
A
au loc relatiile:
A![]() = si A +
= si A + ![]() = 1. Aceste
relatii exprima, in termeni de clase, principiul
noncontradictiei si principiul tertului exclus.
= 1. Aceste
relatii exprima, in termeni de clase, principiul
noncontradictiei si principiul tertului exclus.
Termenii S, P din structura propozitiilor de predicatie determina in universul de discurs patru astfel de clase, si anume:
SP = clasa acelor lucruri care sunt atat S cat si P.
S![]() = clasa acelor lucruri care sunt S, dar nu sunt P.
= clasa acelor lucruri care sunt S, dar nu sunt P.
![]() P = clasa
lucrurilor care nu sunt S, dar sunt P.
P = clasa
lucrurilor care nu sunt S, dar sunt P.
![]()
![]() = clasa acelor lucruri care nu sunt nici S, nici P.
= clasa acelor lucruri care nu sunt nici S, nici P.
Reprezentam aceste clase cu ajutorul urmatoarei diagrame:

Se demonstreaza usor ca suma (reuniunea) acestor clase da 1, adica universul de discurs:
SP + S![]()
![]() P
P ![]()
![]() = SP
+ (1 S)P + S(1 P S P
= SP
+ (1 S)P + S(1 P S P
= SP P SP S - SP 1 - P - S SP
= 1.
Conform diagramelor Venn, cele patru propozitii de predicatie pot fi interpretate dupa cum urmeaza:
SaP S![]() (clasa lucrurilor care sunt S dar nu sunt P este vida).
(clasa lucrurilor care sunt S dar nu sunt P este vida).
SeP SP = (clasa lucrurilor care sunt si S si P este vida).
SiP SP (clasa lucrurilor SP este nevida).
SoP S![]() (clasa lucrurilor S
(clasa lucrurilor S![]() este nevida).
este nevida).
Intr-adevar, a spune ca "Toti S sunt P" este totuna cu a spune ca "nu exista lucruri care sa fie S dar care sa nu fie P" (sau "clasa acelor lucruri care sunt S dar nu sunt P este vida"). La fel, "Nici un S nu este P" se reda prin "Nu exista lucruri care sa fie si S si P" (sau "clasa lucrurilor SP este vida").
Particularelor, in schimb, le corespund clase nevide. "Unii S sunt P" se interpreteaza prin "Exista lucruri care sunt atat S, cat si P", iar "Unii S nu sunt P" inseamna "Exista lucruri care sunt S dar nu sunt P".
Observam ca in citirea (interpretarea) acestor propozitii intervin clase vide si nevide. Clasele vide se prezinta hasurat, iar cele nevide se marcheaza cu un asterix (*).
Conform interpretarilor de mai sus, cele patru propozitii de predicatie vor avea, in final, urmatoarele diagrame Venn:
|
SaP
S |
SeP
SP = |
|
|
|
|
SiP
SP |
SoP
S |
Diagramele Venn, ca si diagramele Euler, reprezinta o prima si foarte simpla interpretare a propozitiilor de predicatie cu ajutorul claselor. In capitolul urmator vom vedea cum se aplica aceste diagrame in testarea validitatii interferentelor.
Termenii propozitiei - subiectul, respectiv, predicatul - au proprietatea de-a fi distribuiti sau nedistribuiti. Se spune despre un termen este distribuit in propozitie daca este luat in toata extensiunea sa si este nedistribuit daca este luat numai dupa o parte a acesteia. De precizat ca nici un termen nu este distribuit in sine, ci numai in propozitia din care face parte.
Unul si acelasi termen poate fi distribuit intr-o propozitie si nedistribuit in alta. De exemplu, termenul "om" este distribuit in propozitia "Toti oamenii sunt muritori" si nedistribuit in propozitia "Unii oameni sunt talentati". Conform principiului noncontradictiei, un termen nu poate fi distribuit si nedistribuit in acelasi timp si sub acelasi raport.
Distributivitatea subiectului Pentru subiect, problema distributivitatii este simpla, cuantorul este cel care ne arata daca termenul subiect este sau nu distribuit. Cand spunem "Toti S sunt P" sau "Nici un S nu este P", sfera lui S se ia in totalitatea sa, asa ca subiectul aici este distribuit. In particulara afirmativa, ca si in particulara negativa, subiectul este nedistribuit intrucat este afectat de cuantorul particular "unii".
Distributivitatea predicatului. Problema predicatului este ceva mai complicata pentru ca, in mod obisnuit, predicatul in propozitie nu este cuantificat. Cum putem noi sti, totusi, cand este el distribuit si cand este nedistribuit?
Trebuie spus ca distributivitatea este o proprietate formala, ea tine de forma propozitiilor si nu de continutul acestora. In forma "Toti S sunt P", ca si in forma "Unii S sunt P", subiectul acopera doar o parte din sfera predicatului, asa ca in ambele cazuri predicatul este nedistribuit. Este drept ca in propozitii ca "Toti oamenii sunt fiinte rationale" sau "Toate insectele sunt hexapode" subiectul si predicatul sunt coextensivi, prin urmare, daca subiectul aici este distribuit, ar trebui ca si predicatul sa fie distribuit. Acestea sunt insa cazuri particulare, cazul general este cel in care sfera subiectului este inclusa in sfera predicatului si atunci predicatul este nedistribuit (doar o parte din predicat este "acoperita" de subiect).
In universala negativa, ca si in particulara negativa, subiectul este separat de intreaga sfera a predicatului, prin urmare, in ambele cazuri predicatul este distribuit.
In tabelul de mai jos "+" inseamna distribuit si "-" nedistribuit.
|
S P |
|
SaPSePSiPSoP |
Prin urmare, subiectul este distribuit in universale si nedistribuit in particulare, iar predicatul este distribuit in negative si nedistribuit in afirmative. Sa mai adaugam ca fiecare din propozitiile SaP, SeP, SiP isi SoP isi are distributivitatea sa, ca nu exista doua astfel de propozitii care sa aibe aceeiasi termeni si aceeasi distributivitate.
Distributivitatea termenilor negativi. Se intampla uneori ca subiectul, respectiv, predicatul logic al unei propozitii sa fie termeni negativi. Daca intr-o asemenea propozitie non-S este distribuit si P nedistribuit, cum vor fi in respectiva propozitie S si non-P, distribuiti sau nedistribuiti?
Nu stiu ca aceasta problema sa fie discutata in manualele si tratatele noastre de logica cu toate ca ea este foarte importanta pentru rationamentele care contin astfel de propozitii.
Inainte de-a incerca un raspuns, sa examinam cateva cazuri particulare.
Exemplul . Fie
propozitia ![]() iP (Unii non-S sunt P). Subiectul propozitiei este non-S si este nedistribuit (ca subiect de particulara).
Dar daca non-S este nedistribuit
in propozitie, cum va fi atunci S,
distribuit sau nedistribuit?
iP (Unii non-S sunt P). Subiectul propozitiei este non-S si este nedistribuit (ca subiect de particulara).
Dar daca non-S este nedistribuit
in propozitie, cum va fi atunci S,
distribuit sau nedistribuit?
Propozitia se
interpreteaza prin ![]() P si
are urmatoarea diagrama Venn:
P si
are urmatoarea diagrama Venn:
|
|
Pentru ca semnul " ", care inseamna "nevid", cade in afara termenului S, acest termen este distribuit fiind vizat in toata extensiunea sa.
Exemplul . Sa examinam acum
propozitia Se![]() (Nici un S nu este
non-P). Conform regulii de
interpretare, obtinem S
(Nici un S nu este
non-P). Conform regulii de
interpretare, obtinem S![]() cu
diagrama:
cu
diagrama:
|
|
Aceasta diagrama corespunde propozitiei SaP (Toti S sunt P), in care S este distribuit si P nedistribuit (tot ce este S este in P, insa o parte a lui P este in afara lui S).
Exemplul 3.
Cum sunt S si P din propozitia ![]() a
a![]() (Toti non-S
sunt non-P)? Aceasta
propozitie se transcrie prin
(Toti non-S
sunt non-P)? Aceasta
propozitie se transcrie prin ![]() P = si
are diagrama:
P = si
are diagrama:
|
|
Pentru ca ![]() P este vida,
inseamna ca tot ce este P
este S, dar exista S care nu sunt P. Prin urmare, P este
distribuit si S nedistribuit.
P este vida,
inseamna ca tot ce este P
este S, dar exista S care nu sunt P. Prin urmare, P este
distribuit si S nedistribuit.
Rezumam acum cele trei situatii cu ajutorul urmatorului tabel:
|
S P, |
|
|
- - + |
Se
|
- - + |
|
- + + - |
Prin generalizare putem introduce urmatoarea regula: daca non-X intr-o propozitie este distribuit, atunci X este nedistribuit si daca non-X este nedistribuit, atunci X este distribuit.
Legile distributivitatii termenilor. Cu ajutorul distributivitatii termenilor se formuleaza doua teoreme ale logicii propozitiilor de predicatie. Prima se refera la deductie si spune ca intr-o inferenta valida (aceasta poate fi un silogism sau o inferenta imediata oarecare), extensiunea termenilor din concluzie nu poate depasi extensiunea lor din premise. Cu alte cuvinte, daca un termen este distribuit in concluzie, el trebuie sa fie distribuit si in premisa care il contine; altfel, inferenta este nevalida.
Teorema este cunoscuta si sub denumirea de "legea distributivitatii termenilor". Vom vedea in capitolul IV ca teorema (legea) distributivitatii termenilor ne poate da o prima si generala idee asupra diferentei dintre rationamentele deductive si cele inductive.
Cea de-a doua teorema se refera la echivalenta propozitiilor: doua sau mai multe propozitii de predicatie care au acelasi subiect si predicat sunt echivalente daca distributivitatea termenilor in propozitii este aceeasi.
De exemplu, in propozitiile:
SaP, Se![]() ,
, ![]() oP si
oP si ![]() i
i![]() intervin termenii S,
P cu sau fara negatii
insa distributivitatea lui S
si P este aceeasi in toate
propozitiile:
intervin termenii S,
P cu sau fara negatii
insa distributivitatea lui S
si P este aceeasi in toate
propozitiile:
|
S P |
||
|
SaP Se
|
|
Avand aceiasi termeni si aceeasi distributivitate a termenilor, cele patru propoitii sunt echivalente (aceasta inseamna ca propozitiile nu pot fi decatadevarate impreuna sau false impreuna si nu una adevarata si una falsa).
Cu ajutorul propozitiilor noi vorbim despre lucruri existente sau presupuse ca existente si nu o data se intampla ca din adevarul propozitiei sa tragem concluzii cu privire la existenta lucrurilor; sau invers, din existenta lucrurilor sa tragem concluzii cu privire la adevarul propozitiilor. Adevarul, asadar, este corelatul logic al existentei, dupa cum existenta este corelatul ontologic al adevarului. De altfel, una din definitiile aristotelice ale adevarului este formulata in termeni de ceea ce este (exista) si ceea ce nu este.
Aceste corespondente logico-ontologice si-au gasit expresia in cunoscuta teza a medievalilor ens et verum convertundur.
In ce fel vorbesc despre existenta propozitiile de predicatie? Cum pot fi interpretate ele existential?
Conform diagramelor Venn, propozitiile
universale neaga existenta in timp ce propozitiile particulare o
afirma. Am vazut ca propozitia "Toti S sunt P" se traduce prin "Nu exista lucruri care sa fie S si non-P" sau "Clasa lucrurilor S![]() este vida". La fel, propozitia universal
negativa "Nici un S nu este P" care inseamna: "Clasa SP este vida", adica "Nu
exista lucruri care sa fie atat S
cat si P".
este vida". La fel, propozitia universal
negativa "Nici un S nu este P" care inseamna: "Clasa SP este vida", adica "Nu
exista lucruri care sa fie atat S
cat si P".
Atat prima cat si a doua propozitie vorbesc despre ceea ce nu exista lasand deschisa problema celor ce exista. Spunand ca nu exista lucruri care sa fie atat S cat si P noi nu afirmam nimic cu privire la existenta, respectiv, nonexistenta lui S, aceasta problema ramane deschisa. La fel in privinta lui P.
Cu totul alta este situatia in cazul propozitiilor particulare unde cuantorul "unii" inseamna "cel putin unul". Dupa cum am vazut intr-un paragraf anterior, propozitia "Unele planete sunt locuite" se interpreteaza prin "Exista ceva (exista x) si acest ceva este planeta si este locuita". Mai simplu: "Exista cel putin o planeta si aceasta planeta este locuita".
Deosebirea este radicala. Propozitiile universale nu presupun existenta, ele pot fi adevarate si fara sa existe lucrurile la care se refera subiectul, respectiv, predicatul logic al propozitiei, in timp ce propozitiile particulare nu pot fi adevarate daca aceste lucruri nu exista.
Cineva ar putea obiecta spunand ca prin asertarea propozitiei "Toti grecii sunt oameni" se aserteaza implicit existenta grecilor.
Logic vorbind, lucrurile nu stau in acest fel.
In primul rand, aici nu este vorba de o singura propozitie, ci de doua propozitii diferite, astfel ca, afirmand-o pe prima noi nu o afirmam, prin aceasta, si pe a doua. Spunand "Toti grecii sunt oameni" noi nu spunem neaparat ca exista greci, ci doar ca daca cineva (ceva) este grec, atunci el este om. "Toti grecii sunt oameni" si "Exista greci" sunt, prin urmare, propozitii diferite, fara legatura una cu cealalta.
Propozitiile universal-negative se interpreteaza la fel; "Nici un centaur nu este ierbivor" devine, conform regulii de interpretare, "Oricare ar fi x, daca x este centaur atunci x este neerbivor". Desi nu exista centauri propozitia este, totusi, adevarata.
De ce o asemenea propozitie este adevarata de vreme ce nu exista centauri?
Folosindu-ne de proprietatile implicatiei am putea spune ca in propozitia "daca x este centaur, x este ierbivor" antecedentul "x este centaur" devine falsa pentru oricare din valorile lui x. Dar o implicatie cu antecedent fals este adevarata, deci si propozitia noastra va fi adevarata in ciuda faptului ca nu exista centauri.
Propozitiile universale sunt, in ultima instanta, ipoteze despre clasele care alcatuiesc subiectul, respectiv, predicatul lor, ipoteze din care nu rezulta daca aceste clase sunt sau nu vide.
Sa luam principiul inertiei din fizica: orice corp tinde sa-si pastreze starea de miscare rectilinie si uniforma sau de repaus relativ atata timp cat asupra lui nu actioneaza alte forte.
Sub aspect logic, principiul este o propozitie universal afirmativa, dar putem noi spune ca exista lucrurile despre care vorbesc subiectul si predicatul logic al propozitiei?
Evident nu, si cu toate acestea propozitia este adevarata. Aceasta pentru ca, asa cum am mai spus, propozitia este o ipoteza: daca asemenea corpuri ar exista, atunci ele ar avea comportamentul dinamic descris. Obiectul invocat in subiectul propozitiei este unul ideal, iar notiunea corespunzatoare lui este, de asemenea, o notiune ideala.
Toate aceste probleme se pot reformula in teoria supozitiilor. Pe scurt, propozitia "Exista S" se deduce din particularele SiP si SoP. Nu se deduce, in schimb, din universalele SaP si SeP. Deci SiP (ca si SoP) nu poate fi adevarata fara sa fie adevarata "Exista S", respectiv, "Exista P" care sunt, conform definitiei, supozitiile ei (supozitii de existenta, se intelege). Vom spune atunci ca propozitiile particulare au supozitii de existenta in timp ce propozitiile universale nu au asemenea supozitii.
Solutia lui Gh. Enescu. O interesanta conceptie in problema supozitiilor de existenta a formulat logicianul roman Gheorghe Enescu[1]. El distinge intre termenii cu sfera reala ai propozitiilor, pe care ii noteaza cu S P, si termenii cu sfera vida, notati S P . Combinandu-se, acesti termeni formeaza patru mari grupe de termeni: (S P S P S P S P ). Corespunzator, vor exista patru tipuri propozitionale:
● Propozitii cu subiect si predicat real (Toate balenele sunt mamifere Unii tineri nu sunt fumatori
● Propozitii cu subiect vid si predicat nevid (Unii zei sunt bipezi Toti extraterestrii sunt violenti
● Propozitii cu subiect nevid si cu predicat vid (Unii oameni sunt nemuritori, Unii cai sunt centauri
Propozitii cu subiect si cu predicat vid (Toti zeii sunt vesnici Unii atlanti sunt venusieni
Pentru ca fiecare grupa contine patru propozitii vor fi, in total, 16 asemenea propozitii. Mai departe, Enescu imparte aceste propozitii in trei grupe, dupa cum urmeaza: 1) propozitii nevide (prima categorie), 2) propozitii semivide (categoria a doua si a treia) si 3) propozitii vide (categoria a patra).
Indiferent de tipul lor, propozitiile de predicatie se transcriu in limbajul logicii predicatelor prin regulile cunoscute:
(1) "Toti S sunt P" s "Oricare ar fi x, daca S(x) atunci P(x)",
(2) "Nici un
S nu este P" s
"Oricare ar fi x, daca S(x),
atunci ![]() ,
,
(3) "Unii S sunt P" s "Exista x astfel ca S(x) si P(x)",
(4) "Unii S nu sunt P" s
"Exista x astfel ca S(x)
si ![]() .
.
Notiunea de adevar pentru propozitiile simple si compuse este precizata de Gh. Enescu prin doua definitii:
Definitia . O propozitie elementara este adevarata daca are loc starea de fapt atomara descrisa de ea.
Definitia . O propozitie compusa este adevarata daca are loc starea de fapt moleculara descrisa de propozitie (de ex. conjunctia starilor de fapt atomare este o stare de fapt moleculara; la fel implicatia starilor atomare, disjunctia lor etc.).
Conform celor doua definitii, propozitiile vide si semivide nu pot fi adevarate intrucat nu exista starile de fapt (atomare sau moleculare) corespunzatoare lor. Din acelasi motiv, ele nu pot fi nici false (ar insemna ca negatiile lor sa fie adevarate).
Voi numi interpretarea lui Gh. Enescu, interpretarea semantica a propozitiilor de predicatie pentru a o deosebi de interpretarea Venn prezentata la inceput. Intre cele doua interpretari diferentele sunt destul de mari. In interpretare Ven, propozitiile: "Toti centaurii sunt ierbivori", "Toti zeii sunt vesnici" etc. sunt adevarate, in timp ce in interpretare semantica, propozitiile nu sunt nici adevarate, nici false.
Cum este atunci propozitia "Unii zei nu sunt vesnici", negatia propozitiei "Toti zeii sunt vesnici"?
In interpretare Venn, propozitia este falsa, in schimb, in interpretare semantica, ea nu este nici adevarata nici falsa.
Relativ la propozitiile de predicatie astfel intelese, Enescu pune doua probleme: i) problema echivalentei propozitiilor si ii) problema implicarii, respectiv, inferarii lor. Solutia celor doua probleme este continuta in urmatoarele teoreme:
Teorema . Daca termenii S, P sunt vizi, atunci raporturile din patratul logic sunt anulate (raporturile dintre propozitiile vide sunt, la randul lor, vide).
Teorema . Daca propozitiile sunt semivide relativ la acelasi termen, atunci propozitiile afirmative sunt false, iar cele negative adevarate.
Teorema . Daca in (1) - (4) introducem operatorii &, ca simple prescurtari pentru expresiile din limbajul natural, atunci obtinem echivalentele:
Toti S sunt P s x (Sx Px),
Nici un S nu este P s x (Sx ![]() ),
),
Unii S sunt P s x (Sx & Px),
Unii S nu sunt P s x (Sx & ![]() ).
).
Teorema . Daca in (1) - (4) operatorii &, au semnificatia lor logico-matematica obisnuita, in locul echivalentelor de mai sus obtinem implicatiile:
Toti S sunt P x (Sx Px),
Nici un S nu este P x (Sx ![]() ),
),
Unii S sunt P x (Sx & Px),
Unii S nu sunt P x (Sx
& ![]() ).
).
Teorema Daca o propozitie este semivida, atunci conversa ei va fi de asemenea semivida.
Interpretarea lui Gh. Enescu este construita, mai corect spus subsumata, teoriei adevarului corespondenta, insa, din cate putem observa, ea se abate de la interpretarea prin diagrame Venn. Interesant este ca pentru propozitiile vide, Enescu admite ceva de genul "nici adevarat, nici fals" ceea ce ar putea sugera o abordare in maniera logicii polivalente.
Probleme speciale ridica, iarasi, propozitiile singulare. Conform cu principiul ontologic, daca o propozitie singulara este adevarata, atunci exista obiectul pe care il denota sau la care se refera subiectul logic al propozitiei. Stiind ca propozitia "Socrate a baut cucuta" este adevarata, noi stim ca a existat un individ cu numele de "Socrate".
Totusi, unele propozitii ridica probleme si in acest caz. Propozitia "Pegas nu exista", de exemplu, s-ar putea reda prin "Pegas este nonexistent". Fiind adevarata ar trebui, conform principiului ontologic, admisa existenta referentului numelui Pegas, referent care nu exista.
Problema era cunoscuta din antichitate, insa, cu toata simplitatea ei, nici astazi nu dispunem de o rezolvare unanim acceptata.
Una dintre solutii, de pilda, considera existenta ca predicat de predicate si nu ca predicat de lucruri individuale (anticipata de Kant, aceasta conceptie si-a gasit dezvoltarea la Frege, dar mai ales la Russell).
Pentru multi autori
existenta nu este doar o proprietate de predicate, ci si o
proprietate a lucrurilor.[2] "Socrate exista", de
exemplu, s-ar traduce prin " x (x = Socrate)", iar "Pegas nu
exista" prin "![]() " sau " x (x Pegas).
" sau " x (x Pegas).
Este drept ca in aceste transcrieri nu avem de-a face cu conceptul de existenta, ci un unul inrudit - conceptul identic cu ceva ce exista (primul caz) si diferit de orice exista (al doilea).
Sa mai notam ca aceleasi probleme se pot formula si in termeni de lumi posibile. Propozitia "Unii zei sunt razbunatori" interpretata prin "Exista ceva care este zeu si razbunator" este falsa in lumea noastra dar este adevarata intr-o alta lume posibila, sa zicem in lumea descrisa de Homer (vezi ontologia logicii formale).
Raporturile de opozitie ale propozitiilor
Ne-am confruntat pana acum cu doua mari raporturi logice dintre propozitii - implicatia si echivalenta. Din logica traditionala s-au pastrat si asa numitele raporturi sau relatii de opozitie. Vom vedea imediat ca si aceste opozitii se definesc pana la urma tot prin implicatie si echivalenta.
Ce sunt, mai intai, aceste opozitii?
Doua propozitii de predicatie sunt in raport de opozitie daca au acelasi subiect si acelasi predicat dar difera prin: 1) calitate, 2) cantitate, 3) atat prin calitate cat si prin cantitate.
Pentru a face cat mai intuitive aceste raporturi ne vom folosi de figura de mai jos in care sunt date elementele structurale ale propozitiilor de predicatie:

Cele doua diagonale delimiteaza un "spatiu logic" propriu fiecarei propozitii in parte:
|
|
|
|
|
|
Axa orizontala reprezinta cantitatea propozitiilor, iar cea verticala calitatea (cele patru propozitii de predicatie sunt simetrice doua cate doua). Prin juxtapunerea celor patru figuri obtinem patru categorii mari de raporturi de opozitie.
Opozitia dintre SaP si SiP, respectiv SeP si SoP:
|
|
|
2) Opozitia dintre SaP si SeP:

3) Opozitia dintre SiP si SoP:

4) Opozitia dintre SaP si SoP, respectiv, SeP si SiP:
|
|
|
Partea hasurata corespunde elementului comun din structura propozitiilor, iar cea nehasurata este partea prin care propozitiile se opun. Intre SaP si SoP, respectiv, SeP si SiP opozitia este totala, propozitiile difera atat prin calitate cat si prin cantitate. Toate celelalte sunt opozitii partiale.
2) Patratul opozitiilor.
Aceste opozitii in calitate si cantitate se rasfrang asupra raporturilor de adevar ale propozitiilor, raporturi pe care le putem defini dupa cum urmeaza:
Raport de subalternare. Are loc intre propozitiile universale si propozitiile particulare de aceeasi calitate, deci intre SaP si SiP si intre SeP si SoP. Propozitiile pot fi impreuna adevarate si impreuna false, si nu una adevarata si alta falsa. Mai exact, adevarul lui SaP implica adevarul lui SiP si falsul lui SiP implica falsul lui SaP (analog pentru SeP si SoP). Simbolic: SaP SiP, SiP SaP, respectiv SeP SoP si SoP SeP
● Raport de contrarietate. Are loc intre universalele de calitate opusa. Propozitiile pot fi false dar nu pot fi adevarate impreuna (adevarul uneia implica falsul celeilalte): SeP SaP si SeP SaP.
● Raport de subcontrarietate. Are loc intre particularele de calitate opusa. Propozitiile pot fi impreuna adevarate, dar nu pot fi impreuna false (falsul uneia implica adevarul celeilalte): SiP SoP si SoP SiP.
● Raport de contradictie. Acest raport are loc intre universalele si particularele de calitate opusa. Propozitiile nu pot fi nici adevarate, nici false impreuna.
In acest raport o propozitie este echivalenta cu negatia celeilalte. SaP s SoP si SeP s SiP (sau SoP s SaP si SiP s SeP).
Impreuna, aceste raporturi formeaza o structura formala cunoscuta sub numele de patrat logic sau patratul logic al opozitiilor.

3. Generalizari in raport cu patratul opozitiilor. Ca si grupul din matematica, patratul logic este o structura formala extrem de generala, el provine din logica propozitiilor de predicatie insa raporturile lui pot fi identificate in mai toate disciplinele si teoriile logicii simbolice. Prin urmare, putem defini aceasta structura formala in general, definitie pe care o vom particulariza, apoi, in diferite domenii.
Fie K o multime compusa din propozitiile X, Y, Z, W intre care au loc relatiile:
R1: X → Y; Z → W (subalternare)
R2 : X→ ~ Z; Z → ~ X (contrarietate)
R3 : ~ Y → W; ~W → Y (subcontrarietate)
R4 : X s ~ W; Z s ~ Y (contradictie)
Sistemul S = este un patrat logic.
In tabelul de mai jos sunt date cateva particularizari ale acestei definitii generale.
|
X |
Y |
Z |
W |
|
|
P1 |
SaP |
SiP |
SeP |
SoP |
|
P2 |
P& Q |
P Q |
P Q |
P↓Q |
|
P3 |
P Q |
Q P |
P Q |
Q P |
|
P4 |
xF(x) |
xF(x) |
x F(x) |
x F(x) |
|
P5 |
x Fx Gx |
x Fx & Gx) |
x Fx Gx |
x Fx & ~Gx) |
|
P6 |
Lp |
Mp |
Up |
Qp |
P1 este patratul logic al propozitiilor de predicatie pe care tocmai l-am discutat; P2 si P3 sunt structuri de patrat definite in logica propozitiilor; P4 si P5 sunt structuri de patrat specifice logicii predicatelor. In fine, P6 este patratul logic al modalitatilor despre care urmeaza sa discutam chiar in acest capitol.
4. Patratul opozitiilor in interpretare existentiala. Sa revenim la patratul logic al propozitiilor de predicatie. Intrebarea este: mai sunt valabile raporturile acestui patrat daca propozitiile sunt interpretate existential?
Raspunsul este negativ pentru ca:
● Propozitiile SaP si SiP, respectiv, SeP si SoP nu mai sunt in raport de subalternare. Daca nu exista martieni, propozitia "Toti martienii sunt pasnici" este adevarata, iar "Unii martieni sunt pasnici" este falsa. Acelasi lucru este valabil si pentru propozitiile negative.
● Propozitiile SaP si SeP nu mai sunt contrare. Neexistand martieni, propozitiile "Toti martienii sunt pasnici" si "Nici un martian nu este pasnic" sunt impreuna adevarate.
● Propozitiile SiP si SoP nu mai sunt subcontrare. Propozitiile "Unii martieni sunt pasnici" si "Unii martieni nu sunt pasnici" sunt impreuna false.
Asadar, in interpretarea existentiala din patratul logic raman doar raporturile de contradictie (propozitiile SaP si SeP sunt adevarate, iar SiP si SoP false).
9. Propozitiile de predicatie in conceptia lui Fl. Tutugan
Logicianul roman Florea Tutugan a studiat propozitiile de predicatie folosind un raport semantic special bazat pe raporturile logice ale termenilor. El a observat, de pilda, ca propozitia universal afirmativa "Toti S sunt P" este adevarata in doua cazuri: 1) cand S este inclus in P, ca in propozitia "Toti oameni sunt fiinte bipede", si 2) cand S este identic cu P, ca in propozitia "Toti oamenii sunt fiinte rationale". Practic, intre propozitia "Toti oamenii sunt fiinte bipede" si propozitia "Toti oamenii sunt fiinte rationale" nu exista diferenta de forma cu toate ca in prima propozitie subiectul este coextensiv predicatului, iar in a doua subiectul este doar subordonat predicatului.
Prin urmare, forma "Toti S sunt P" exprima disjunctia raporturilor de identitatea si subordonare a termenilor (vezi diagramele Euler).
Ce raporturi sau disjunctii de raporturi intre termeni sunt proprii celorlalte propozitii de predicatie? Aceasta este intrebarea.
Diagramele Euler nu ne pot ajuta
in rezolvarea problemei din simplul motiv ca nu reproduc intreaga
gama a raporturilor dintre termeni si, in plus, nu au capacitatea
sa reproduca raporturile dintre negatiile termenilor. Stim,
de exemplu, care sunt raporturile dintre S
si P specifice propozitiei
"Toti S sunt P", dar ce raporturi determina
aceasta propozitie intre termenii ![]() si
si ![]() ?
?
Concluzia autorului este ca mai inainte de-a studia raporturile logice ale propozitiilor trebuie cunoscute foarte bine raporturile termenilor in general, fiecare propozitie exprimand o anume disjunctie de asemenea raporturi.
In Silogistica judecatilor de predicatie, Tutugan reia ideea unuia dintre studiile lui mai vechi si identifica sapte raporturi posibile ale termenilor pe care le numeste "raporturi unice si bine determinate". Din pacate, terminologia autorului, ca si simbolistica folosita de el, sunt greoaie si destul de neobisnuite de aceea scrierile lui nu sunt foarte accesibile ancepatorului.
Data fiind importanta acestor cercetari, redau cateva din rezultatele obtinute de Fl. Tutugan in logica propozitiilor de predicatie folosind, pe cat posibil, terminologia logicii actuale.
Fie doi termeni generali S,
P si negatiile acestora ![]() ,
, ![]() . Exista, dupa Fl. Tutugan, sapte
raporturi posibile ale acestor termeni, si anume:
. Exista, dupa Fl. Tutugan, sapte
raporturi posibile ale acestor termeni, si anume:
I. Identitate:
S = P, ![]() =
= ![]()
II. Subordonare: S P, ![]()
![]() ,
,
III. Supraordonare:
P S, ![]()
![]() ,
,
IV. Contradictie:
S = ![]() ,
, ![]() = P,
= P,
V. Contrarietate: S ![]() , P
, P ![]() ,
,
VI. Subcontrarietate:
![]() P,
P, ![]() S,
S,
VII. Incrucisare: S P, ![]()
![]() .
.
Este interesant ca raporturilor in extensiune ale termenilor, autorul le asociaza raporturi de intensiune corespunzatoare. De pilda, identitatii (raport intre extensiuni) ii corespunde echivalenta (raport intre intensiuni). Subordonarea (raport de extensiune) se traduce in intensiune prin "implicatie stricta directa" (terminologia autorului), iar supraordonarea prin "implicatie stricta inversa". Contrarietatii ii corespunde ca rapor de intensiune "excluderea stricta necontradictorie", iar incrucisarii "indiferenta implicativa".
Dupa ce clarifica aceste probleme, Tutugan arata ce disjunctii pot fi stabilite intre cele sapte relatii unice si bine determinate.
Un calcul simplu arata ca exista, in total, 120 de asemenea disjunctii insa nu toate sunt relevante pentru studiul propozitiilor de predicatie.
Aici apare un prim element de noutate in logica lui Tutugan datorat asocierii propozitiilor de predicatie cu anume disjunctii de raporturi intre termeni. In opinia lui, aceste disjunctii sunt responsabile de echivalentele propozitiilor ca si de raporturile inferentiale ale acestora.
Iata cele patru propozitii de predicatie si disjunctiile lor specifice:
Toti S sunt P Nici un S nu este P
I sau II IV sau V
Unii S sunt P Unii S nu sunt P .
I sau II sau III sau VI sau VII III sau IV sau V sau VI sau VII
Din cate observam, propozitiile universale A si E sunt dublu indeterminate cuprinzand fiecare disjunctia a doua raporturi unice si bine determinate in timp ce particularele I si O sunt quintuplu indeterminate avand fiecare asociata o disjunctie de cinci raporturi. Concret:
● Propozitia "Toti S sunt P" inseamna:
"S =
P sau
S P", respectiv, "![]() =
= ![]() sau
sau ![]()
![]() ".
".
● Propozitia "Nici un S nu este P" inseamna:
"S =
![]() sau S
sau S ![]() ", respectiv, "
", respectiv, "![]() = P sau P
= P sau P
![]() ".
".
● Propozitia "Unii S sunt P" inseamna:
"S =
P sau
S P sau
P S sau
![]() P sau
S P", respectiv, "
P sau
S P", respectiv, "![]() =
= ![]() sau
sau ![]()
![]() sau
sau ![]()
![]() sau
sau ![]() S sau
S sau
![]()
![]() ".
".
● Propozitia "Unii S nu sunt P" inseamna:
"P S sau
S = ![]() sau S
sau S ![]() sau
sau ![]() P sau S P", respectiv, "
P sau S P", respectiv, "![]()
![]() sau
sau ![]() = P sau P
= P sau P ![]() sau
sau ![]() S sau
S sau ![]()
![]() ".
".
Observam, de asemenea, ca disjunctia propozitiei SaP este cuprinsa in disjunctia propozitiei SiP dar este complementara disjunctiei aferente lui SoP. Analog pentru SeP si SiP. In general, propozitiile afirmative contin raportul de identitate si exclud contradictia, iar propozitiile negative contin contradictia si exclud identitatea. Particularele cuprind obligatoriu incrucisarea, iar universalele, identitatea si una din subordonari.
Doua propozitii caracterizate prin disjunctia acelorasi raporturi sunt echivalente intre ele. Este un prim rezultat al logicii lui Fl. Tutugan, insa, pana sa ajungem la aceste probleme se impune o alta observatie: pe langa disjunctiile propozitiilor A, E, I, O, propozitii din "prima grupa" cum le numeste Fl. Tutugan, exista si o a doua grupa formata din propozitiile A', E', I', O' . Acestea sunt propozitiile de predicatie A, E, I, O cu termeni negativi.
Propozitia A' este propozitia "Toti ![]() sunt
sunt ![]() ", I' este
propozitia "Unii
", I' este
propozitia "Unii ![]() sunt
sunt ![]() " si asa mai departe. Cele patru propozitii
isi au disjunctiile lor proprii, respectiv:
" si asa mai departe. Cele patru propozitii
isi au disjunctiile lor proprii, respectiv:
![]()
![]() Toti
Toti ![]() sunt
sunt ![]() Nici
un
Nici
un ![]() nu este
nu este ![]()
I sau III IV sau VI
![]()
![]() Unii
Unii ![]() sunt
sunt ![]() Unii
Unii![]() nu sunt
nu sunt ![]()
I sau II sau III sau V sau VII II sau IV sau V sau VI sau VII
Avand in vedere ca propozitiile care desemneaza aceleasi disjunctii de raporturi unice si bine determinate sunt echivalente intre ele, putem determina clasele de echivalenta pentru fiecare propozitie in parte.
Propozitia A Propozitia E
a) Toti S sunt P, a) Nici un S nu este P,
b) Nici un S nu este non P, b) Toti S sunt non P,
c) Toti non P sunt non S, c) Nici un P nu este S,
d) Nici un non P nu este S. d) Toti P sunt non S.
Propozitia I Propozitia O
a) Unii S sunt P, a) Unii S nu sunt P,
b) Unii S nu sunt non P, b) Unii S sunt non P,
c) Unii P sunt S, c) Unii non P nu sunt non S,
d) Unii P nu sunt non S. d) Unii non P sunt S.
Propozitia A' Propozitia E'
a) Toti non S sunt non P, a) Nici un non S nu este non P,
b) Nici un non S nu este P, b) Toti non S sunt P,
c) Toti P sunt S, c) Nici un non P nu este non S,
d) Nici un P nu este non S. d) Toti non P sunt S.
Propozitia I' Propozitia O'
a) Unii non S sunt non P, a) Unii non S nu sunt non P,
b) Unii non S nu sunt P, b) Unii non S sunt P,
c) Unii non P sunt non S, c) Unii P nu sunt S,
d) Unii non P nu sunt S. d) Unii P sunt non S.
Propozitiile care apartin aceleiasi clase sunt echivalente intre ele.
Conform definitiei judecatii pe care am dat-o la inceputul acestui capitol, vom spune ca fiecare clasa corespunde unei judecati anume, deci exista 32 de propozitii care exprima, in total, 8 judecati.
In maniera de notare adoptata, K(I), de exemplu, este judecata exprimata de propozitia "Unii S sunt P" si de toate propozitiile logic echivalente cu ea. Aceleasi raporturi logice care exista intre judecati vor exista si intre propozitiile care exprima respectivele judecati.
Revenind la echivalentele acestor propozitii, logica traditionala le-a studiat numai in legatura cu inferentele imediate insa la Fl. Tutugan ele au o cu totul alta pondere. Metoda lui, de inspiratie logic-semantica, i-a permis nu doar reconstructia silogisticii, ci si o noua perspectiva asupra inferentelor imediate si, bineinteles, asupra altor probleme ale logicii formale.
Acestea sunt echivalentele propozitiilor din prima grupa, insa, in logica lui Tutugan, la fel de importante sunt si echivalentele din cea de-a doua grupa (grupa propozitiilor cu termeni negativi) precum si raporturile reciproce ale propozitiilor din cele doua grupe.
Solutia lui Tutugan, singura existenta pana la aceasta data, are la baza urmatoarele definitii formulate de autor in termenii relatiilor sale "unice si bine determinate":
Definitia . Doua propozitii sunt echivalente atunci cand reprezinta disjunctia acelorasi raporturi unice.
Definitia .Doua propozitii sunt in raport de contradictie daca nu contin nici o relatie unica in comun, iar suma celor pe care le contin este egala cu toate cele sapte relatii unice si bine determinate (fiecare propozitie cuprinde relatiile pe care nu le contine cealalta propozitie).
Definitia . O propozitie P implica propozitia Q daca disjunctia lui Q contine toate raporturile pe care le contine disjunctia lui P si contine cel putin o asemenea relatie in plus. Cele doua propozitii sunt in raport de supraalternare, respectiv, subalternare.
Definitia . Doua propozitii sunt in raport de contrarietate daca nu au nici o relatie in comun dar suma lor nu echivaleaza cu cele sapte raporturi unice si bine determinate.
Definitia Doua propozitii sunt in raport de subcontrarietate daca poseda cel putin o relatie ireductibila in comun, fiecare contine cel putin o relatie in plus fata de cealalta, iar suma componentelor lor echivaleaza cu cele sapte raporturi unice.
Definitia . Doua propozitii sunt independente logic (sau indiferente implicativ) daca poseda cel putin o relatie in comun, fiecare contine o relatie in plus fata de cealalta, iar suma lor nu echivaleaza cu cele sapte raporturi unice.
Aplicand aceste definitii celor doua grupe de propozitii, Tutugan ajunge la urmatoarele raporturi ale patratului logic:
● Contradictie: (A, O), (E, I), (A', O'), (E', I').
● Contrarietate: (A, E), (A, E'), (A', E), (A', E').
● Subcontrarietate: (I, O), (I, O'), (I', O), (I', O').
● Subalternare: (A, I), (A, I'), (A', I), (A', I'), (E, O), (E, O'), (E', O), (E', O').
● Supraalternare: (I, A), (I, A'), (I', A), (I', A'), (O, E), (O, E'), (O', E), (O', E').
● Indiferenta: (A, A'), (E, E'), (A, O'), (A', O), (E, I'), (E', I), (I, I') si (O, O').
Cu aceasta am determinat toate opozitiile posibile ale propozitiilor de predicatie. Observam ca fata de raporturile traditionalului patrat logic au aparut acum o serie de raporturi noi care intregesc tabloul general al opozitiilor logice. De pilda, contradictia nu are loc numai intre A si O, respectiv, intre E si I, cum stiam din logica clasica, ci si intre A' si O', respectiv, E' si O'.
Surprize mari aduce si subalternarea. Propozitia A subalterneaza nu doar propozitia I, ci si pe I', iar A' o subalterneaza nu doar pe I', ci si pe I. La fel, in ce priveste propozitiile negative.
Curios este ca intre A si O', E si I', A' si I, E' si O nu exista nici un fel de opozitie, aceste propozitii sunt indiferente implicativ. La fel propozitiile I si I', respectiv, O si O'. Neavand raporturi implicative, intre aceste propozitii nu vor exista nici raporturi inferentiale.
|
Politica de confidentialitate |
| Copyright ©
2024 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |