
![]()
in care S este suprafata sm2t.
![]()
unde t este timpul, in sst sau sht.
Caldura se poate transmite intre corpuri prin conductie termica, convectie termica sau radiatie termica.
Conductia termica este modul de transmitere a caldurii dintr-o zona cu temperatura ridicata catre o zona cu temperatura coborata, in interiorul unui corp sau intre corpuri solide aflate in contact direct, fara deplasari aparente ale particulelor care formeaza corpurile respective. Ecuatia fundamentala pentru transmiterea caldurii prin conductie este relatia lui Fourier (1822):
![]()
in care l este coeficientul de conductivitate termica sW/m·Kt, iar dt reprezinta variatia elementara de temperatura dupa directia x pe care are loc schimbul de caldura. Coeficientul de conductivitate termica reprezinta cantitatea de caldura transmisa prin conductie, in unitatea de timp, intre doua planuri paralele din corpul considerat, situate la distanta de un metru unul de celalalt; propagarea caldurii are loc pe o directie perpendiculara pe cele doua suprafete.
Convectia termica reprezinta procesul de schimb de caldura dintre un perete si un fluid, atunci cand exista o diferenta de temperatura intre perete si fluid; convectia presupune existenta unei miscari a particulelor ce alcatuiesc fluidul. Daca miscarea apare doar ca urmare a modificarii densitatii fluidului odata cu temperatura, convectia se numeste naturala; atunci cand miscarea este determinata de forte exterioare (produse de o pompa, un ventilator etc.), convectia se numeste fortata.
Ecuatia fundamentala a convectiei termice este data de relatia lui Newton (1701):
![]()
unde a este coeficientul de transfer al caldurii prin convectie sW/m2·Kt, iar Dt este diferenta de temperatura s0Ct. Coeficientul de convectie reprezinta cantitatea de caldura transmisa in unitatea de timp, prin unitatea de suprafata, la o diferenta de temperatura de 10C.
Radiatia termica este procesul de transmitere a caldurii intre corpuri aflate la temperaturi diferite, separate in spatiu, pe baza energiei electromagnetice. Relatia de baza a radiatiei termice este ecuatia Stefan-Boltzmann:
![]()
in care ![]() este coeficientul de radiatie al corpului
negru, iar T este temperatura
corpului sKt.
este coeficientul de radiatie al corpului
negru, iar T este temperatura
corpului sKt.
3.1. Transmiterea unidirectionala a caldurii, prin conductie, printr-un perete plan omogen
Folosind notatiile din fig. A.3 si aplicand relatia lui Fourier putem scrie:
![]()
sau, separand variabilele:
![]()
de unde, prin integrare intre limite:
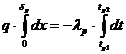
rezulta:
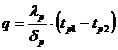
Utilizand notatia:
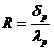
in care R este rezistenta termica, intensitatea fluxului de caldura transmis prin conductie devine:

|
|
Fig. A.3 - Transmiterea caldurii prin conductie, prin perete plan omogen dp-grosimea peretelui; lp-conductivitatea termica a materialului peretelui. |
Se observa ca in cazul in care conductivitatea termica este constanta, temperatura variaza liniar pe grosimea peretelui.
3.2. Transmiterea unidirectionala a caldurii, prin conductie, printr-un perete plan multistrat
Pentru acest caz peretele plan se considera a fi format din mai multe straturi omogene; caldura se transmite perpendicular pe perete (fig. A.4). Pentru fiecare strat component al peretelui se poate scrie relatia determinata anterior pentru peretele plan omogen:
![]()
|
|
Fig. A.4 - Transmiterea caldurii prin conductie printr-un perete multistrat |
Presupunand ca fluxurile de caldura transmise prin straturi sunt aceleasi (nu se pierde caldura prin incalzirea straturilor), adica q = q1 = q2 = q3, rezulta:

Adunand relatiile obtinem:
![]()
si in final rezulta intensitatea fluxului de caldura:

sau:
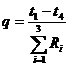
in care Ri este rezistenta termica a stratului i.
3.3. Transmiterea unidirectionala a caldurii, prin conductie, printr-un perete cilindric omogen
In acest caz se porneste de la relatia de definitie a fluxului de caldura:
![]()
Utilizand notatiile din fig. A.5 si tinand cont de faptul ca propagarea caldurii se face radial, aplicand ecuatia lui Fourier rezulta:
![]()
in care l este lungimea cilindrului.
Aplicand metoda separarii variabilelor obtinem:
![]()
Integrand relatia intre limite:

obtinem:
![]()
deci rezulta ca distributia temperaturii in peretele cilindric este de tip logaritmic.
|
|
Fig. A.5 - Transferul de caldura prin conductie, printr-un perete cilindric omogen l-lungimea; di-diametrul interior; de-diametrul exterior. |
Fluxul de caldura transmis prin conductie, prin peretele cilindric omogen, va fi:
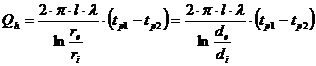
in care re si ri sunt raza exterioara si respectiv interioara ale cilindrului, iar de si di sunt diametrul exterior si respectiv interior.
3.4. Transmiterea unidirectionala a caldurii, prin conductie, printr-un perete cilindric multistrat
In acest caz se considera peretele cilindric ca fiind format din mai multe straturi omogene (fig. A.6); pentru fiecare strat se poate aplica relatia determinata anterior pentru peretele omogen format dintr-un singur strat:
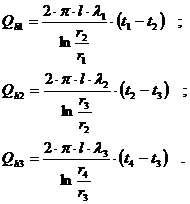
Se pune conditia Qh = Qh1 = Qh2 = Qh3 si, procedand ca si in cazul peretelui plan multistrat, rezulta in final:
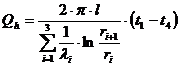
|
|
Fig. A.6 - Transferul de caldura prin conductie, prin perete cilindric multistrat |
3.5. Transmiterea unidirectionala a caldurii, prin conductie si convectie
Majoritatea schimbatoarelor de caldura asigura transmiterea caldurii intre doua fluide, separate printr-un perete metalic. In acest caz, transmiterea caldurii se realizeaza prin convectie intre fluide si perete si prin conductie prin materialul peretelui.
In fig. A.7 este prezentat cazul transmiterii caldurii intre doua fluide, separate printr-un perete plan omogen.
|
|
Fig. A.7 - Transmiterea caldurii prin conductie si convectie, prin perete plan omogen |
Transmiterea caldurii prin convectie se face conform legii lui Newton:
Transmiterea caldurii prin peretele omogen respecta relatia stabilita anterior (vezi 3.1):
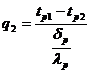
Se pune conditia:
q = q1 = q2 = q3
si dupa prelucrarea relatiilor anterioare, obtinem:
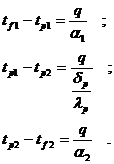
Adunand relatiile obtinem in final:

Se noteaza rezistenta termica ca fiind:
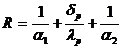
si intensitatea fluxului de caldura se poate scrie sub forma:
![]()
In cazul in care peretele plan este multistrat (de exemplu format dintr-un strat de piatra depusa din apa, un strat metalic si un strat de vopsea la exterior), relatia pentru intensitatea fluxului de caldura va fi:
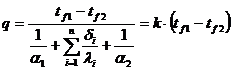
in care n este numarul de straturi ce formeaza peretele, iar k este coeficientul global de schimb de caldura, determinat cu relatia:
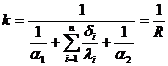
Pentru cazul schimbului de caldura intre doua fluide separate printr-un perete cilindric omogen, (fig. A.8), fluxurile de caldura transmise prin convectie vor fi:
|
|
Fig. A.8 - Transmiterea caldurii prin conductie si convectie, prin perete cilindric omogen |
Pentru conductia prin peretele cilindric se utilizeaza relatia determinata anterior (vezi 3.3):
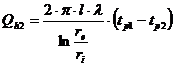
Ca si in cazurile anterioare se pune conditia Qh = Qh1 = Qh2 = Qh3 si obtinem in final:

Pentru peretele cilindric multistrat fluxul de caldura va fi dat de relatia:
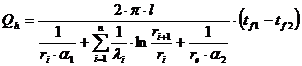
in care n este de asemenea numarul de straturi ce formeaza peretele cilindric.
3.5. Schimbul de caldura prin suprafete extinse s5, 15t
Prin suprafete extinse se inteleg suprafetele de schimb de caldura prevazute cu aripioare sau nervuri. In cazul gazelor, pentru care coeficientii de transfer prin convectie au valori mici, existenta suprafetelor extinse permite cresterea suprafetei de schimb de caldura si deci asigura marirea fluxului de caldura transmis.
Aripioarele pot avea forme diverse (rectangulare, circulare etc.), iar in sectiune longitudinala pot avea forma paralelipipedica, de triunghi etc.
In tehnica frigului suprafetele nervurate se utilizeaza in constructia vaporizatoarelor si condensatoarelor.
Pentru nervura se defineste randamentul nervurii h, definit ca raportul intre fluxul termic efectiv transmis si fluxul termic maxim, ce ar putea fi transmis daca temperatura pe intreaga lungime a aripioarei ar fi egala cu temperatura la baza acesteia (in realitate, temperatura scade de la baza catre varf).
Pentru cazul unui perete plan prevazut cu nervuri rectangulare (fig. A.9), la care fluidul de pe partea cu nervuri este un gaz, se noteaza cu Sn suprafata nervurata si cu S' suprafata peretelui cuprinsa intre nervuri. Suprafata totala de schimb de caldura pe partea gazului va fi:
![]()
Daca Qh este fluxul de caldura transmis, pe partea cu aripioare acesta are doua componente:
![]()
unde Qn este fluxul transmis prin nervuri, iar Q' este fluxul transmis prin suprafata dintre nervuri.
|
|
Fig. A.9 - Schimbul de caldura prin suprafete extinse an - coeficient de transfer de caldura prin convectie, pentru nervuri; a' - coeficient de transfer de caldura prin convectie, pentru suprafata dintre nervuri; l - conductivitatea termica a materialului; d - grosimea peretelui. |
Folosind randamentul termic al aripioarei si aplicand relatia lui Newton pentru transferul de caldura prin convectie, putem scrie:
![]()
in care h este randamentul aripioarei, iar Qn,max este fluxul termic maxim ce poate fi transmis daca temperatura este aceasi pe toata lungimea aripioarei (egala cu temperatura de la baza acesteia).
Fluxul de caldura transmis prin spatiul dintre aripioare va fi:
![]()
Rezulta ca fluxul total de caldura transmis pe partea dinspre fluidul rece se va calcula cu relatia:
![]()
Se defineste un coeficient echivalent de transfer prin convectie, pentru fata nervurata:
![]()
iar din egalitatea fluxurilor de caldura determinate prin cele doua relatii rezulta:
![]()
Din ecuatiile fluxului de caldura obtinem egalitatile:
![]()
iar in final rezulta fluxul de caldura transmis:
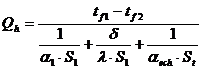
sau:
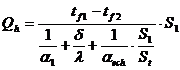
ori:
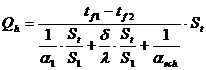
Raportul St/S1 se numeste coeficient de nervurare si are valori cuprinse intre 2 si 20, in functie de tipul nervurilor.
Folosind notatiile:
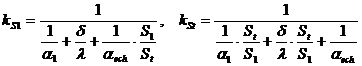
care definesc coeficientii globali de schimb de caldura, fluxul de caldura se poate scrie si sub urmatoarele forme:
![]()
sau
![]()
Schimbatoarele de caldura sunt aparate termice in care are loc transferul caldurii de la un fluid cu temperatura mai ridicata (fluid termic primar) catre un fluid cu temperatura mai mica (fluid termic secundar), in procese de incalzire, racire, vaporizare, condensare sau in procese termice complexe.
In functie de modul de realizare a transferului de caldura, schimbatoarele de caldura pot fi: aparate cu contact indirect si aparate cu contact direct.
Schimbatoarele cu contact indirect (de suprafata) sunt aparate la care cei doi agenti termici nu sunt in contact direct, ei fiind separati de o suprafata de schimb de caldura cu care vin in contact permanent sau periodic.
Atunci cand cele doua fluide vin in contact permanent cu suprafata de schimb de caldura, schimbatorul de caldura este de tip recuperativ. In figura A.10 este prezentat schematic cel mai simplu aparat de acest tip, schimbatorul cu tevi concentrice; unul dintre fluide circula prin interiorul tevii centrale, celalalt prin spatiul dintre cele doua tevi.
|
|
Fig. A.10 - Schimbator de caldura recuperativ. |
Daca agentii termici vin in contact alternativ cu suprafata de transfer de caldura, fluxul termic schimbandu-si periodic directia, schimbatorul de caldura este de tip regenerativ. Aparatele regenerative pot fi realizate cu suprafata fixa (figura A.11a) sau rotativa (figura A.11b).
|
|
|
Fig. A.11 - Schimbatoare de caldura regenerative a-schimbator regenerativ cu umplutura fixa; b) schimbator regenerativ rotativ. |
Schimbatoarele de caldura cu contact direct sunt aparate la care agentii termici nu mai sunt separati de o suprafata, ei amestecandu-se unul cu celalalt. Acestea pot fi aparate fara umplutura, la care transferul de caldura se realizeaza la suprafata fluidului pulverizat in picaturi fine sau care curge in suvite (fig. A.12a), sau aparate cu umplutura, la care transferul termic apare la suprafata unei pelicule formate pe umplutura schimbatorului (fig. A.12b).
|
|
Fig. A.12 - Schimbatoare de caldura cu contact direct a) fara umplutura; b) cu umplutura. |
|
|
|
Fig. A.13 - Tipuri principale de curgere a) contracurent; b) echicurent; c) curent incrucisat, ambele fluide amestecate; d) curent incrucisat, un fluid amestecat si celalalt neamestecat; e) curent incrucisat, ambele fluide neamestecate |
|
In functie de modul in care are loc curgerea fluidelor, schimbatoarele de caldura pot fi (fig. A13):
Curgerea in contracurent presupune ca cei doi agenti termici circula pe langa suprafata de schimb de caldura paralel si in sensuri contrarii. Curgerea in contracurent asigura cea mai mare diferenta medie de temperatura intre agentii termici, insa temperatura peretelui la intrarea fluidului cald este maxima.
Curgerea in echicurent apare in cazul circulatiei agentilor termici paralel si in acelasi sens, pe langa suprafata de transfer de caldura. Acest tip de curgere realizeaza cea mai mica diferenta medie de temperatura, insa cea mai buna racire a peretelui in zona de intrare a fluidului primar.
Circulatia in curent incrucisat presupune curgerea perpendiculara a celor doi agenti termici. In acest caz se pot distinge trei situatii: ambele fluide amestecate, un fluid amestecat si celalalt neamestecat, ambele fluide neamestecate.
Un fluid se numeste 'neamestecat' atunci cand are aceeasi temperatura in orice plan normal pe directia sa de curgere, deci temperatura sa variaza numai in lungul curgerii. In cazul fluidului 'amestecat' exista o diferenta de temperatura si in planul normal la directia de curgere.
In cazul in care agentii termici au mai multe treceri prin tevi sau manta curgerea este compusa (fig. A.14), aceasta fiind o combinatie intre cele trei tipuri anterioare de curgere.
|
|
|
Fig. A.14 - Schimbatoare de caldura avand curgere compusa a) o trecere prin manta si doua treceri prin tevi; b) doua treceri prin manta si patru treceri prin tevi; c) o trecere prin manta si trei treceri prin tevi; d) trei treceri prin manta si sase treceri prin tevi. |
Calculul schimbatoarelor de caldura se face pornind de la ecuatiile de bilant termic si de transfer termic.
Ecuatia de bilant termic este:
![]()
unde ![]() este fluxul de caldura cedat de catre fluidul
primar (cald),
este fluxul de caldura cedat de catre fluidul
primar (cald), ![]() este fluxul
de caldura primit de catre fluidul secundar, iar
este fluxul
de caldura primit de catre fluidul secundar, iar ![]() reprezinta fluxul de caldura pierdut spre
exteriorul aparatului.
reprezinta fluxul de caldura pierdut spre
exteriorul aparatului.
Fluxurile de caldura schimbate de catre fluide sunt date de relatiile (vezi si fig. A.15):
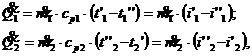
in care:
|
|
|
Fig. A15 - Elemente pentru calculul schimbatoarelor de caldura |
Ecuatia de transfer termic se scrie sub forma generala:
![]()
unde k este coeficientul global de schimb de caldura, S este aria suprafetei prin care are loc schimbul de caldura, iar Dtmed este diferenta medie de temperatura dintre cele doua fluide.
Pentru schimbatoarele de caldura avand curgere paralela (fig. A.15) se utilizeaza diferenta medie logaritmica de temperatura:

in care Dtmax este diferenta maxima dintre temperaturile celor doi agenti, iar Dtmin este diferenta de temperatura minima.
Pentru schimbatoarele de caldura avand curgere neparalela, diferenta medie de temperatura se determina cu relatia:
![]()
unde F este un factor de corectie, iar DtmedCC este diferenta medie logaritmica de temperatura, determinata pentru un schimbator de caldura in contracurent (fig. A.15b) la care temperaturile de intrare si de iesire ale fluidelor sunt aceleasi ca si in cazul aparatului pentru care se face calculul.
Factorul de corectie F se determina din diagrame trasate pentru fiecare schema de curgere neparalela, in functie de parametrii P si R.
Criteriul P are sensul unei eficacitati termice, fiind definit ca raportul dintre gradul de incalzire al agentului secundar in aparat si diferenta maxima disponibila:
![]()
Criteriul R reprezinta raportul intre capacitatile termice ale celor doi agenti termici:
![]()
Pentru calculul efectiv al schimbatorului de caldura se poate utiliza o metoda grafo-analitica, care presupune reprezentarea grafica a intensitatii fluxurilor de caldura pentru fiecare fluid in parte.
De exemplu, pentru cazul condensatorului racit cu aer al unei
instalatii frigorifice, temperatura agentului primar este
Se calculeaza diferenta de temperatura medie logaritmica Dtmed, cu relatia anterioara; temperatura medie a aerului va fi:
![]()
Intensitatea fluxului termic pe partea agentului frigorific este:
![]()
in care a este coeficientul de schimb convectiv de caldura pentru agentul frigorific, iar tp este temperatura peretelui schimbatorului.
Intensitatea fluxului termic pe partea aerului se determina cu relatia:
![]()
unde k este coeficientul global de schimb de caldura .
Cele doua intensitati ale fluxului termic se reprezinta grafic, pentru diverse valori ale temperaturii peretelui (fig. A.16).
In punctul de intersectie al celor doua curbe se determina
temperatura tp a peretelui schimbatorului si intensitatea fluxului
termic ![]() .
Cunoscandu-se intensitatea fluxului de caldura, se poate calcula suprafata de
schimb de caldura, pornind de la sarcina termica a condensatorului (care rezulta
din calculul termic al instalatiei frigorifice):
.
Cunoscandu-se intensitatea fluxului de caldura, se poate calcula suprafata de
schimb de caldura, pornind de la sarcina termica a condensatorului (care rezulta
din calculul termic al instalatiei frigorifice):
![]()
unde F este sarcina termica sWt.
Pentru calculul coeficientului de transfer al caldurii prin convectie si a coeficientului global de schimb de caldura se folosesc relatii specifice, care tin cont de regimul de curgere al celor doua fluide, de tipul schimbatorului de caldura etc.
|
|
Fig. A.16 - Principiul metodei grafo-analitice |
Conceptul de schimbator de caldura cu placi a aparut la inceputul acestui secol, acestea fiind initial destinate necesitatilor industriei laptelui; ulterior, utilizarea lor s-a extins in diverse alte ramuri ale industriei: chimie, tehnica nucleara etc. Conceptul nu a fost suficient exploatat pana la Richard Seligman, fondatorul APV International Ltd, prima firma ce a comercializat, incepand cu anul 1923, schimbatoare de caldura cu placi si garnituri. Initial placile erau din gunmetal , dar din 1930 acestea au inceput sa fie realizate din otel inoxidabil. Primele aparate de acest tip erau limitate din punct de vedere al conditiilor de functionare la o presiune de maximum 2 bar si o temperatura de aproximativ 60 °C. De atunci, schimbatoarele de caldura cu placi si garnituri au ramas practic neschimbate din punct de vedere constructiv si al tehnologiei de fabricatie, dar dezvoltarile din ultimii saizeci de ani au condus la ridicarea parametrilor operationali (presiune, temperatura) la 30 bar si respectiv 180°C, ca urmare a varietatii materialelor din care sunt realizate placile si garniturile de etansare.
In fig. A.17 este prezentata o clasificare a schimbatoarelor de caldura cu placi.
Schimbatoarele cu suprafata primara sunt cele mai raspandite, placile metalice asigurand separarea celor doua fluide de lucru. In cazul schimbatoarelor cu suprafata secundara, intre placi se gaseste o umplutura metalica.

Fig. A.17 - Tipuri de schimbatoare de caldura cu placi
In principiu, un schimbator de caldura cu placi este format din placile metalice (3, fig. A.18), realizate prin ambutisare, astfel incat sa se creeze canale pentru circulatia fluidelor. Prin canalele (2), formate pe o fata a unei placi din pachet circula agentul primar, in timp ce agentul secundar circula circula prin canalele (3), formate pe cealalta fata a placii.
|
|
Fig. A.18 - principiul de functionare al schimbatorului de caldura cu placi 1-placa metalica; 2-canale pentru circulatia agentului primar; 3-canale pentru circulatia agentului secundar. |
In cazul schimbatoarelor cu placi si garnituri, placile (4) ale schimbatorului sunt fixate pe sine (1, fig. A.19) si sunt stranse cu ajutorul tirantilor (7) si al placilor de presiune (2) si (6). Placile de capat (3) si (6) au configuratii speciale, pentru a dirija agentii de lucru.
Grosimea unei placi este de 0,4.0,8 mm, aceasta fiind prevazuta cu garniturile (2, fig. A.20), care asigura etanseitatea traseelor agentilor si circulatia alternativa a acestora intre canale. Din fig. A.21 se observa ca agentul de lucru care circula prin racordul (2) poate trece pe fata vizibila a placii schimbatorului de caldura, in timp ce traseul agentului care circula prin racordul (1) este etansat fata de aceasta parte a placii. Diametrul canalelor prin care circula agentii sunt cuprinse, in general, intre 1,5 si 11 mm, in functie de presiunea de lucru (diametre mari la presiuni de lucru mici) si de natura fluidelor.
Garniturile sunt elemente care limiteaza presiunile si temperaturile maxime in schimbatoarele de caldura in placi; din acest motiv, in unele cazuri se utilizeaza garnituri duble.
|
|
Fig. A.19 - Schimbator de caldura cu placi 1-sina; 2, 6-placi de presiune; 3, 5-placi de capat; 6-pachet de placi; 7-tirant. |

Fig. A.20 - Circulatia agentilor de lucru printr-un schimbator cu placi
1- placa; 2-garnitura; 3-circulatia agentului primar; 4-circulatia agentutlui secundar.
|
|
Fig. A.21 - Dirijarea agentilor de lucru cu ajutorul garniturilor 1-traseu izolat: 2-traseu deschis. |
In fig. A.22 sunt prezentate diferite varinate de circulatie ale agentilor prin schimbatorul de caldura; si pentru aceste schimbatoare sunt valabile variantele de baza: curgere in echicurent si respectiv curgerea in contracurent. De obicei este preferata curgerea in contracurent.
|
a) |
b) |
|
Fig. A.22 - Scheme de circulatie ale agentilor a-o singura trecere pentru ambii agenti; b-mai multe treceri, in numar egal pentru cei doi agenti. |
|
Profilul placii are o importanta deosebita, acesta trebui sa asigure o curgere turbulenta a fluidelor prin canale, pentru obtinerea unui coeficient mare al transferului convectiv de caldura; in acelasi timp trebuie asigurata o distributie cat mai uniforma a fluidelor pe intreaga suprafata a placilor, dar si prezenta unor puncte de sprijin intre suprafetele metalice ale placilor alaturate, astfel inat aparatul sa aiba o rigiditate corespunzatoare. La ora actuala sunt brevetate peste 60 de geometrii diferite ale placilor, unele dintre acestea fiind prezentate in fig. A.23.
|
|
|
|
|
|
|
|
|
Fig. A.23 - Geometrii ale placilor schimbatoarelor cu placi si garnituri |
||
Atunci cand este foarte important sa se evite contaminarea unui agent de lucru de catre cel de al doilea agent se apeleaza la solutia dublarii placilor schimbatorului de caldura (fig. A.24).
Cele mai frecvent utilizate materiale pentru realizarea placilor sunt prezentate in tabelul A.3.5.1, iar in tabelul A.3.5.2 sunt prezentate materialele utilizate pentru garnituri.
|
|
Fig. A.24 - Dublarea placilor pentru evitarea contaminarii agentilor de lucru 1-garnitura; 2, 3-placi metalice. |
Tabelul A.3.5.1
Materiale metalice pentru placi
|
Materialul |
Caracteristici |
|
Otel inoxidabil tip 304 |
C - max. 0,08%; Mn - max. 2%; Cr-max. 20%; Ni - max. 10,5%; rezistenta la rupere - min. 515 MPa. |
|
Otel inoxidabil tip 316 |
C - max. 0,08%; Mn - max. 2%; Cr - 16.18; Ni - 10.16%; Mo - 2.3% rezistenta la rupere - min. 515 MPa. |
|
Otel inoxidabil tip 317 |
C - max. 0,08%; Mn - max. 2%; Cr - 18.20%; Ni - 11.15%; Mo - 3.4% rezistenta la rupere - min. 515 MPa. |
|
Monel |
Ni - 65.70%; Cu - 20.29%; Fe, Mn - max. 5%; rezistenta la rupere - 550 MPa. |
|
Inconel |
Ni - 50.72%; Cr - 14.21%; Fe - 5.10%; Mn - 0,5.1%; rezistenta la rupere - 68.900 MPa. |
|
Bronz de aluminiu |
aliaj Cu - Al (4.1%) - alte metale (Fe, Ni, Mn etc.). |
Tabelul A.3.5.2
Materiale pentru garnituri
|
Materialul |
Temperatura maxima de lucru soCt |
|
Acrilonitril | |
|
Izobutan-izopropan | |
|
Etilena-propilena (EPDM) | |
|
Fluorcarbon (Viton) |
Schimbatoarele de caldura cu placi sudate sau lipite permit cresterea presiunii si temperaturii maxime deoarece nu se utilizeaza elemente de etansare; presiunile de lucru pentru astfel de aparate pot atinge 40.50 bar, in timp ce temperatura maxima a fluidelor de lucru poate fi de 450.500 oC.
Aceste schimbatoare au o constructie asemanatoare, in principiu, cu cea a schimbatoarelor cu placi si garnituri, fiind de asemenea formate din placi metalice intre care sunt realizate canale, fiecare fata a unei placi aflandu-se in contact cu unul dintre cei doi agenti de lucru. Placile sunt insa sudate intre ele (fig. A.25) si ca urmare a acestui fapt schimbatoarele nu au nici garnituri de etansare si nici tiranti care sa asigure strangerea pachetului de placi.
|
|
Fig. A.25 - Placi sudate 1-canal pentru circulatia agentului de lucru: 2-sudura; 3, 4-placi metalice. |
|
a) |
b) |
|
Fig. A.26 - Schimbatoare de caldura sudate a-sectiune; b-vedere de ansamblu. |
|
Fata de schimbatoarele cu placi si garnituri, schimbatoarele cu placi sudate sunt mai compacte si au preturi mai mici; in schimb, acestea nu pot fi demontate pentru curatare.
Principalele elemente geometrice caracteristice schimbatoarelor de caldura cu placi rezulta din fig. A.27; acestea sunt:
|
a) |
|
b) |
|
Fig. A.27 - Dimensiuni geometrice pentru schimbatoarele de caldura cu placi |
Diametrul hidraulic (echivalent) este definit de relatia generala:
![]()
in care Sc este sectiunea de curgere, iar P este perimetrul udat, perpendicular pe directia principala de curgere.
Pentru calculul termic al unui schimbator de caldura cu placi, suprafata de schimb de caldura avuta in vedere este:
![]()
unde n este numarul de placi, iar Sp este suprafata unei placi sm2t.
Ecuatia criteriala a schimbului de caldura va fi:

in
care Nu este numarul Nusselt, ![]() este criteriul Reynolds,
este criteriul Reynolds, ![]() este criteriul Prandtl, w este viteza de
circulatie a fluidului sm/st h este vascozitatea
dinamica sN s/m2t, r este densitatea skg/m3t, n este vascozitatea cinematica sm2/st, l este
conductivitatea termica sW/m Kt, iar cp este caldura specifica sJ/kg Kt; Prp
este numarul Prandtl corespunzator temperaturii peretelui canalului.
este criteriul Prandtl, w este viteza de
circulatie a fluidului sm/st h este vascozitatea
dinamica sN s/m2t, r este densitatea skg/m3t, n este vascozitatea cinematica sm2/st, l este
conductivitatea termica sW/m Kt, iar cp este caldura specifica sJ/kg Kt; Prp
este numarul Prandtl corespunzator temperaturii peretelui canalului.
Coeficientii a si b depind de unghiul de ondulare b, de pasul relativ p/H0 si de regimul de curgere, caracterizat prin numarul Reynolds; in tabelul A.3.5.3 sunt prezentate unele valori ale acestor coeficienti
Tabelul A.3.5.3
Valorile constantelor a si b
|
b s0t |
a |
b |
Re |
|
p/H0 = 2 |
|||
|
p/H0 = 3,33 |
|||
Pentru cazul in care Pr > 1 (situatie valabila pentru majoritatea agentilor lichizi) in literatura de specialitate se propune si relatia criteriala:
![]()
Calculul termic al unui schimbator de caldura cu placi, urmarind determinarea numarului necesar de placi, se desfasoara dupa un proces iterativ, pe baza fluxului termic pe care trebuie sa-l asigure aparatul; calculul se desfasoara conform schemei logice din fig. A.28.
Pierderile de presiune intr-un schimbator de caldura cu placi sunt date de rezistenta hidraulica a pachetului de placi, de rezistentele locale ale racordurilor de intrare si iesire si de modificarile de inaltime ale traseului. Relatia de calcul a caderii totale de presiune pentru unul din agentii de lucru este:

in care:
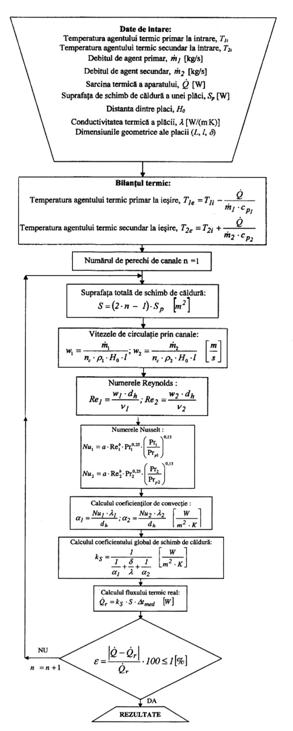
Fig. A.28 - Algoritmul de calcul pentru proiectarea unui schimbator de caldura cu placi
Coeficientul de frecare f se determina in functie de numarul Reynolds al curgerii prin aparat:
![]()
folosind una din relatiile:
|
| |
|
sau | |
|
|
Valorile constantelor a si b necesare calculului caderii de presiune sunt prezentate in tabelele A.3.5.4 si A.3.5.5.
Pentru ultimul termen al relatiei de calcul a caderilor de presiune se considera semnul + atunci cand sensul de deplasare al agentului este in sus si semnul - atunci cand agentul se deplaseaza in jos
Tabelul A.3.5.3
Valorile constantelor a si b (p/H0 = 2)
|
b s0t |
a |
b |
Re |
|
< 2500 |
|||
|
> 2500 |
|||
|
30 (relatia 2) | |||
|
30 (relatia 1) | |||
|
45 (relatia 2) | |||
|
45 (relatia 1) | |||
|
60 (relatia 2) | |||
|
60 (relatia 1) | |||
|
72 (relatia 2) | |||
|
72 (relatia 1) | |||
|
90 (relatia 2) | |||
|
90 (relatia 1) |
Tabelul A.3.5.4
Valorile constantelor a si b (p/H0 = 3,33)
|
b s0t |
a |
b |
Re |
|
< 2500 |
|||
|
> 2500 |
|||
|
Politica de confidentialitate |
| Copyright ©
2024 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |