
ANALIZA SI SINTEZA MECANISMELOR CU CAMA
Mecanismele cu cama se numara printre cele mai simple si cele mai des folosite mecanisme. Ele sunt compuse in principal din cama si tachet. Cama este de obicei elementul (motor) conducator, iar tachetul elementul (antrenat) condus. Aceste mecanisme pot fi plane sau spatiale; marea majoritate sunt plane, studiul celor spatiale putandu-se reduce la studiul unora plane.
Cama este elementul profilat a carui forma, alaturi de tipul si dimensiunile elementelor mecanismului, determina legea de miscare a tachetului. Contactul dintre cama si tachet (sau rola lui) formeaza o cupla superioara (bimobila), care poseda doua mobilitati: rotatie si translatie dupa o directie tangentiala.
1. Clasificarea mecanismelor cu cama.
Clasificarea se refera la mecanisme formate doar din cama si tachet (inclusiv rola tachetului daca este cazul), legate ambele la baza. Se mentioneaza ca exista si mecanisme complexe, care contin elemente ca: roti dintate, parghii benzi elastice etc., care impreuna cu elementele cama si tachet, contribuie la obtinerea unor legi de transmitere complexe. In unele situatii cama si/sau tachetul pot sa nu fie legate direct la baza. Se mai face specificatia ca, o serie de alte tipuri de mecanisme continand una sau mai multe cuple bimobile, pot fi considerate, pentru o fractiune a ciclului cinematic, ca putandu-se reduce tot la tipul de mecanism cama-tachet. In acest sens se poate da exemplul mecanismelor: cu roti stelate, cu clichet, tip cruce de Malta etc.
1.1. Criterii de clasificare.
a) Criteriul tipului curbei descrise de punctul (teoretic) de contact dintre cama si tachet distinge: mecanisme plane si spatiale. Sistemul de axe in care se analizeaza curba-loc geometric al punctului de contact, se considera pe rand solidar atat cu cama cat si cu tachetul. Daca in ambele situatii locurile geometrice sunt continute intr-un acelasi plan, mecanismul este plan in orice alta situatie, mecanismul este spatial.
b) Criteriul (analitic) parametric, aplicabil mecanismelor plane. In cadrul acestui criteriu, in cazurile cand tachetul este prevazut si cu rola, aceasta se considera parte integranta a tachetului, ea neinfluentand cinematica mecanismului ci doar transformand frecarea de alunecare in frecare de rostogolire.
Pentru tipologia mecanismelor cu cama (fig. 126.) se considera urmatorii patru parametrii principali
![]() , raza vectoare a punctului de contact in raport cu centrul
, raza vectoare a punctului de contact in raport cu centrul ![]() de rotire al camei
de rotire al camei
![]() , raza de curbura a tachetului in punctul de contact cu cama
, raza de curbura a tachetului in punctul de contact cu cama
![]() , raza vectoare a centrului de curbura al tachetului in raport cu centrul
, raza vectoare a centrului de curbura al tachetului in raport cu centrul
![]() de oscilatie al
tachetului
de oscilatie al
tachetului
![]() , distanta orientata
, distanta orientata ![]() .
.
Corelatia dintre acesti parametrii este:
![]()
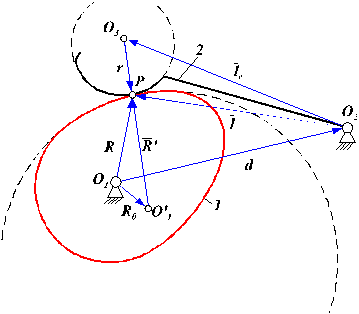
Fig. 126.
Daca se face o anliza calitativa a modulelor parametrilor,
se observa ca fiecare, in mod teoretic, poate trece prin urmatoarele stari zero
(0), finit variabil (var.), finit constant (ct.), infinit ( ). Deci in mod teoretic: R, ![]() ,
, ![]() ,
, ![]() I
I
La o analiza in detaliu, se remarca unele situatii imposibile (de excludere)
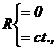
![]()
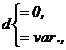 (1)
(1)
si unele situatii cu caracter de obligativitate (de restrictie) pentru existenta unui mecanism cu cama:
![]()
![]() (2)
(2)
implicate de starea ![]() . La randul ei, starea
. La randul ei, starea ![]() este implicata de
situatiile:
este implicata de
situatiile:
![]() cu
cu ![]() in planul finit,
in planul finit,
![]() cu
cu ![]() in planul finit (3)
in planul finit (3)
![]() .
.
Situatiile descrise prin relatiile anterioare conduc insa si la
![]() (4)
(4)
cu specificarea, in acest caz, a implicatiei ![]()
Tinand cont de relatiile (1).(4), se ajunge la concluzia ca pentru mecanismele plane cu cama, caracterizanti sunt parametrii r si d. Atunci tipologia parametrica a acestor mecanisme va fi descrisa de trecerea prin cele patru stari posibile ale lui r si d.
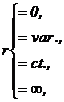
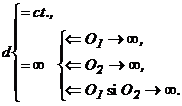
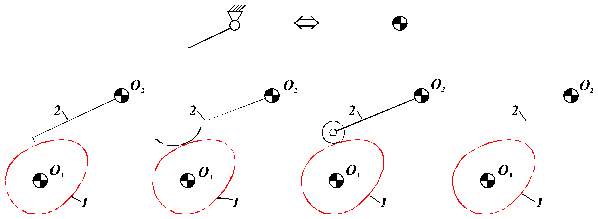 Rezulta (fig. 127, 128, 129, 130) 16 variante - tipuri de
mecanisme cu cama.
Rezulta (fig. 127, 128, 129, 130) 16 variante - tipuri de
mecanisme cu cama.
a. b. c. d.
r=0, d=finit=ct. r=finit=var, d=finit=ct. r=finit=ct., d=finit=ct. r , d=finit=ct.
Fig. 127.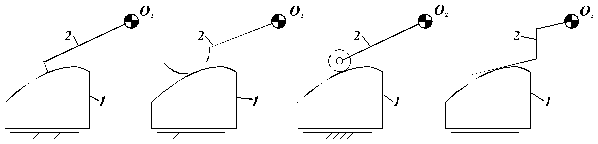
a. b. c. d.
r=0, d= O r=finit=ct., d= O
r=finit=var, d= O r , d= O
Fig. 128.
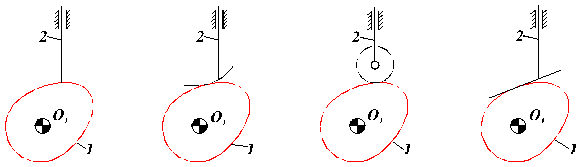
a. b. c. d.
r=0, d= O r=finit=ct., d= O
r=finit=var, d= O r , d= O
Fig. 129.
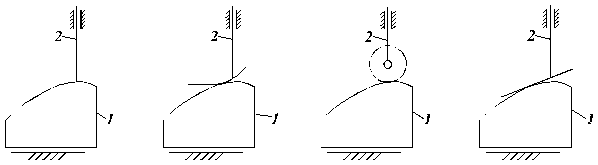 a. b. c. d.
a. b. c. d.
r=0, d= O O r=finit=ct., d= O O
r=finit=var, d= O O r , d= O O
Fig. 130.
Se folosesc uzual urmatoarele denumiri:
![]() -
tachet cu varf ascutit
-
tachet cu varf ascutit
![]() -
tachet curbiliniu
-
tachet curbiliniu
![]() -
tachet cu rola
-
tachet cu rola
![]() -
tachet plat sau cu talpa
-
tachet plat sau cu talpa
![]() - cama
de rotatie si tachet oscilant
- cama
de rotatie si tachet oscilant
![]() - cama
de translatie si tachet oscilant
- cama
de translatie si tachet oscilant
![]() - cama
de rotatie si tachet de translatie
- cama
de rotatie si tachet de translatie
![]() - cama si tachet
de translatie
- cama si tachet
de translatie
Cazul mecanismului avand cama de
translatie si tachet plat de translatie, exprimat parametric prin ![]() , este un caz degenerat, deoarece traiectoria punctului de
contact intr-un plan solidar cu cama, este o curba degenerata la un punct fix
(fig. 130, d).
, este un caz degenerat, deoarece traiectoria punctului de
contact intr-un plan solidar cu cama, este o curba degenerata la un punct fix
(fig. 130, d).
 In
acest caz mecanismul cu cama, poate fi considerat ca degenerand intr-un
mecanism (plan) cu pana (fig. 131).
In
acest caz mecanismul cu cama, poate fi considerat ca degenerand intr-un
mecanism (plan) cu pana (fig. 131).
c) Criteriul tipului de inchidere a cuplei superioare, deosebeste mecanisme cu cupla superioara inchisa datorita fortei sau formei. Inchiderea prin forma este o solutie mai costisitoare, dar se impune acolo unde sunt necesare forte foarte mari sau acolo unde nu se poate realiza pe parcursul unui intreg ciclu cinematic, dezvoltarea unei forte de directie si modul corespunzator inchiderii cuplei (de exemplu la camele de turatie moderata dar la care raza maxima a camei este mult mai mare decat raza minima).
2. Elemente geometrice si notatii.
Marea majoritate a mecanismelor cu cama realizeaza un ciclu cinematic complet al tachetului, in urma unui ciclu cinematic complet al camei. Fac exceptie unele mecanisme, utilizate la masini-unelte, la masini de forjat orizontale etc.
In cazul cand tachetul este prevazut cu rola, centrul rolei va descrie o echidistanta - denumita profil teoretic - a profilului real pe care se rostogoleste rola.
Fazele geometrice ale unui ciclu cinematic al tachetului sunt:
faza a: urcarea (ridicarea, indepartarea) - in cazul acestei faze vitezele tachetului se considera pozitive
faza b: stationarea (pauza) in pozitie superioara
faza c: coborarea (apropierea)
faza d: stationarea (pauza) in pozitie inferioara.
Faza b si/sau d pot lipsi (ca de exemplu o cama circulara excentrica actonand orice tip de tachet).
Din punct de vedere dinamic, faza geometrica in timpul careia trebuiesc invinse fortele utile (tehnologice), se numeste faza activa. Faza activa poate fi urcarea (de obicei), sau poate fi si coborarea sau chiar ambele.
Parametrul independent care pozitioneaza
elementul 1 cama, in cazul miscarii
ei de rotatie, este marimea ei unghiulara ![]() sau
sau ![]() . Parametrul dependent care pozitioneaza elementul 2 tachetul este unghiul
. Parametrul dependent care pozitioneaza elementul 2 tachetul este unghiul ![]() (la tachetul oscilant)
sau marimea
(la tachetul oscilant)
sau marimea ![]() (la tachetul cu
miscare de translatie).
(la tachetul cu
miscare de translatie).
Se vor utiliza urmatoarele notatii:
![]() timpul [s];
timpul [s];
![]() unghiul camei corespunzator fazei de
urcare a tachetului;
unghiul camei corespunzator fazei de
urcare a tachetului;
![]() unghiul corespunzator fazei de
stationare superioara;
unghiul corespunzator fazei de
stationare superioara;
![]() unghiul corespunzator fazei de coborare
unghiul corespunzator fazei de coborare
![]() unghiul corespunzator fazei de
stationare inferioara;
unghiul corespunzator fazei de
stationare inferioara;
![]() viteza unghiulara a camei [
viteza unghiulara a camei [![]() ];
];
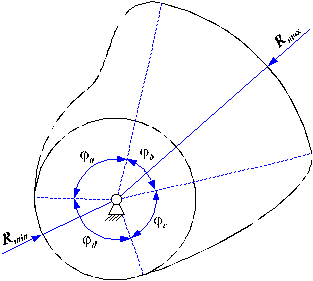
Fig. 132.
cu cama de rotatie.
![]() raza minima a camei in raport cu
centrul ei de rotire [mm];
raza minima a camei in raport cu
centrul ei de rotire [mm];
![]() raza maxima a camei [mm];
raza maxima a camei [mm];
![]() raza curenta de curbura a profilului
camei in punctul de
raza curenta de curbura a profilului
camei in punctul de
contact cu tachetul [mm];
![]() raza rolei tachetului [mm];
raza rolei tachetului [mm];
![]() unghiul initial care pozitioneaza
tachetul oscilant, in cadrul
unghiul initial care pozitioneaza
tachetul oscilant, in cadrul
fazei de stationare in pozitie inferioara
![]() viteza unghiulara a tachetului oscilant
[
viteza unghiulara a tachetului oscilant
[![]() ];
];
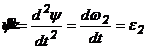 acceleratia unghiulara a tachetului
oscilant;
acceleratia unghiulara a tachetului
oscilant;
![]() viteza unghiulara redusa a tachetului
oscilant cand cama este
viteza unghiulara redusa a tachetului
oscilant cand cama este
de rotatie [adimensional];
![]() acceleratia unghiulara redusa a
tachetului oscilant
acceleratia unghiulara redusa a
tachetului oscilant
cand cama este de rotatie [adimensional];
![]() spatiul initial, care pozitioneaza
tachetul de translatie
spatiul initial, care pozitioneaza
tachetul de translatie
in cadrul fazei de stationare in pozitie inferioara [mm];
![]() viteza liniara a tachetului de
translatie [mm/s];
viteza liniara a tachetului de
translatie [mm/s];
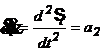 acceleratia liniara a tachetului [
acceleratia liniara a tachetului [![]() ];
];
![]() viteza liniara redusa a tachetului de
translatie al unui
viteza liniara redusa a tachetului de
translatie al unui
mecanism cu cama de rotatie [mm];
![]() acceleratia liniara redusa a tachetului
de translatie al unui
acceleratia liniara redusa a tachetului
de translatie al unui
mecanism cu cama de rotatie [mm];
3. Analiza mecanismului cama-tachet.
Consta in studiul mecanismului, cand
se cunosc parametrii geometrici ai mecanismului (profilul camei si tachetului,
alte dimensiuni) si de miscare ai camei element conducator (![]() ,
, ![]() ). Se cer determinate legile de miscare ale tachetului (
). Se cer determinate legile de miscare ale tachetului (![]() ,
, ![]() sau
sau ![]() ,
, ![]() ).
).
Exista doua metode:
Metoda directa care consta in desenarea in pozitii succesive a profilului camei, determinandu-se legea de miscare a spatiului tachetului.
Metoda inversa care consta in aplicarea virtuala asupra intregului mecanism a unei miscari egale ca modul dar inversa ca sens cu cea a camei. In acest caz, unui observator exterior cama ii va apare virtual imobila, tachetul urmarind, impreuna cu ghidajul sau, profilul camei. Si in acest caz se poate ridica legea de miscare (transmitere) a spatiului tachetului.
In continuare, la ambele metode, se trece la derivari succesive (grafice sau analitice) a legii de spatiu determinandu-se legea de transmitere a vitezelor, acceleratiilor tachetului, s.a.m.d.

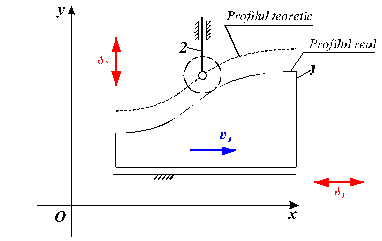
Fig. 133.
Mecanism cu cama de translatie - metoda directa.
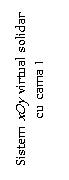
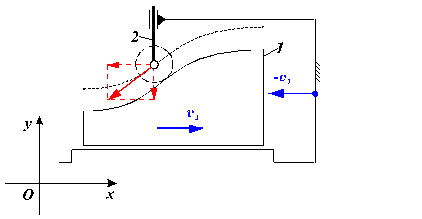
Fig. 134.
Mecanism cu cama de translatie - metoda inversa miscarii.
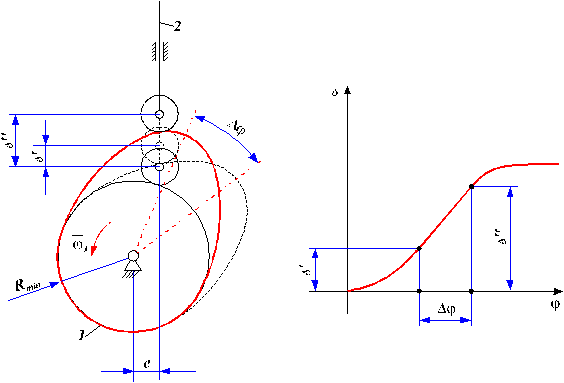
Fig. 13
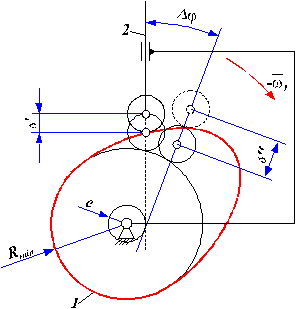
Fig. 136.
Mecanism cu cama de rotatie - metoda inversiunii miscarii
4. Sinteza mecanismelor cu cama.
Consta in determinarea profilului camei atunci cand se impun anumite performante miscarii tachetului.
Date de intrare: inaltimea de
ridicare h sau y, unghiurile
de rotatie ale camei, unghiurile de presiune maxime ![]() (dintre directia
fortei dezvoltata de cama asupra tachetului, echivalenta cu normala comuna nn in punctul de contact cu cama si
directia vitezei punctului de contact apartinand tachetului), legea de variatie
a acceleratiilor (daca aceasta nu se da, proiectantul trebuie sa-si aleaga una
in concordanta cu procesul tehnologic in care intervine mecanismul cu cama) de
ordinul I sau de ordin superior.
(dintre directia
fortei dezvoltata de cama asupra tachetului, echivalenta cu normala comuna nn in punctul de contact cu cama si
directia vitezei punctului de contact apartinand tachetului), legea de variatie
a acceleratiilor (daca aceasta nu se da, proiectantul trebuie sa-si aleaga una
in concordanta cu procesul tehnologic in care intervine mecanismul cu cama) de
ordinul I sau de ordin superior.
4.1. Mecanisme cu cama de translatie si tachet de translatie
cu varf ascutit avand legea de variatie a acceleratiilor
sinusoidala sau cosinusoidala.
In acest caz prin doua integrari succesive se obtine analitic chiar profilul camei in portiunea de ridicare, indepartare.
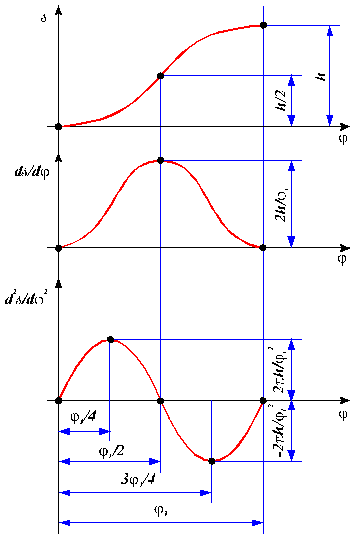
Fig. 137.
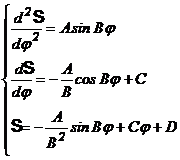
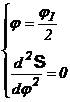
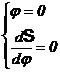
![]()
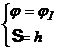
![]()
![]()
![]()
![]()
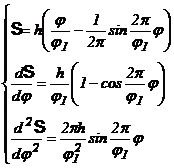
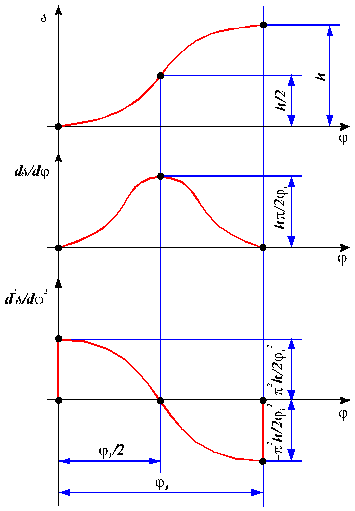
Fig. 138.
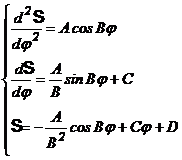
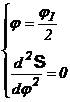
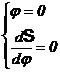
![]()
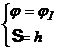
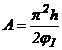
![]()
![]()
![]()
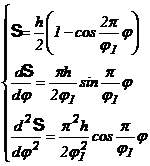
4.2. Stabilirea semnului excentricitatii la mecanismele
cu cama de rotatie si tachet de translatie.
Excentricitatea, in
acest caz, este reprezentata de distanta constanta de la centrul de rotatie ![]() al camei, la suportul
vectorului viteza liniara a varfului tachetului sau centrului de rotatie al
rolei. Excentricitatea poate fi ori pozitiva, ori negativa, ori nula. Semnul ei
se stabileste pozitiv sau negativ, dupa cum punctele BI si FI au vitezele liniare de acelasi sens sau de sens opus in
timpul fazei de ridicare sau indepartare a tachetului.
al camei, la suportul
vectorului viteza liniara a varfului tachetului sau centrului de rotatie al
rolei. Excentricitatea poate fi ori pozitiva, ori negativa, ori nula. Semnul ei
se stabileste pozitiv sau negativ, dupa cum punctele BI si FI au vitezele liniare de acelasi sens sau de sens opus in
timpul fazei de ridicare sau indepartare a tachetului.
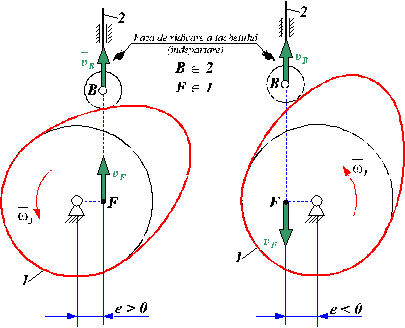
Fig. 139.
4.3. Determinarea lui ![]() la mecanismele cu cama
de rotatie
la mecanismele cu cama
de rotatie
si tachet de translatie cu varf ascutit.
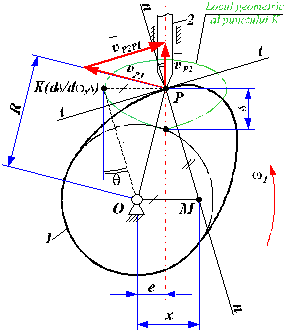
Pentru determinarea ![]() , se construieste diagrama
, se construieste diagrama ![]() , locul geometric al punctului K. La aceasta se duc tangentele ce fac cu axe paralele cu ordonata
unghiul
, locul geometric al punctului K. La aceasta se duc tangentele ce fac cu axe paralele cu ordonata
unghiul ![]() respectiv unghiul
respectiv unghiul 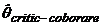 . Astfel se determina zona hasurata, zona in care se poate
amplasa centrul de rotatie al camei
. Astfel se determina zona hasurata, zona in care se poate
amplasa centrul de rotatie al camei ![]() . Apoi, daca se impune
. Apoi, daca se impune ![]() , se determina corespunzator
, se determina corespunzator ![]() , daca nu se considera
, daca nu se considera ![]() care implica o e unica.
care implica o e unica.
Fig. 140.
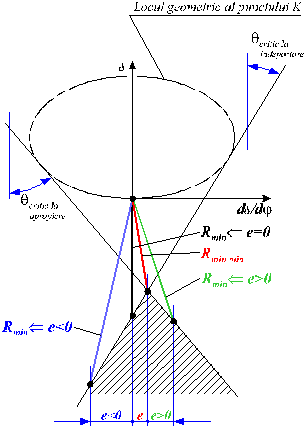
Fig. 141.
![]() cu
cu ![]()
![]()
![]()
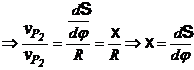
Atunci K
este asociat
perechii ![]() .
.
Conditia ![]() este satisfacuta
pentru orice centru de rotatie O al
camei, ales in zona hasurata (fig. 141) - inclusiv frontierele.
este satisfacuta
pentru orice centru de rotatie O al
camei, ales in zona hasurata (fig. 141) - inclusiv frontierele.
Cea mai mica raza minima: ![]() .
.
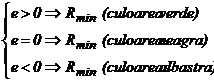
4.4. Determinarea ![]() la mecanismele cu cama
de rotatie
la mecanismele cu cama
de rotatie
si tachet plat (cu talpa) de translatie.
In acest caz exista
doua proceduri pentru determinarea celei mai mici raze minime ![]() .
.
Fie se construieste 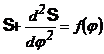 , si apoi
, si apoi ![]() este modulul celei mai
mari ordonate negative (fig. 144, a), fie se construieste curba
este modulul celei mai
mari ordonate negative (fig. 144, a), fie se construieste curba 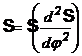 , se duce tangenta sub
, se duce tangenta sub ![]() la ramura de abscise
negative a curbei,
la ramura de abscise
negative a curbei, ![]() reprezentand distanta
de la intersectia acestei tangente cu ordonata pana la originea sistemului
(fig. 144, b).
reprezentand distanta
de la intersectia acestei tangente cu ordonata pana la originea sistemului
(fig. 144, b).
Se va lua apoi ![]() .
.
La
mecanismele cu cama de rotatie si tachet plat (cu talpa) de translatie ![]() este intotdeauna egal
cu zero. Trebuie insa aleasa o
este intotdeauna egal
cu zero. Trebuie insa aleasa o ![]() astfel incat sa nu
apara concavitati.
astfel incat sa nu
apara concavitati.

a.
b.
Fig. 142.
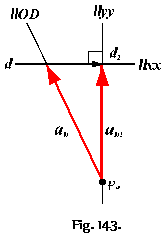
![]()
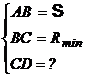
Mecanismul
inlocuitor are ![]() ,
, ![]() fiind raza de curbura
a camei in punctul A.
fiind raza de curbura
a camei in punctul A.
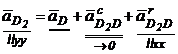
![]()
![]()
![]() dar
dar ![]()
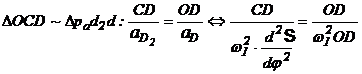
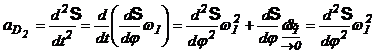
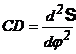
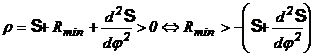
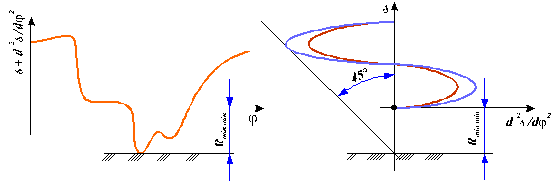
a. b.
Fig. 144.
Sinteza legilor de miscare a camelor
cu pulsul redus constant
(functie treapta)
Varietatea - ca tipuri - a mecanismelor cu cama este extrem de mare. Dintre acestea, marea majoritate este constituita din mecanisme care lucreaza la viteze mici si mijlocii. Astfel se poate da exemplul masinilor unelte automate, al masinilor textile, agricole, ale motoarelor lente cu combustie interna, al masinilor si dispozitivelor de forta si/sau comanda al utilajelor prelucratoare avand asemenea mecanisme etc.
Daca in cazul mecanismelor rapide cu cama exista o metodologie de proiectare bine pusa la punct si devenita chiar clasica (este vorba de camele polinomiale), in cazul mecanismelor cu cama pentru viteze mici sau mijlocii exista in literatura de specialitate doar fie indicatii cu caracter general, fie metode cu interes numai teoretic. De aceea in continuare, se va da o metoda completa si pusa la punct, adaptabila la cele mai diverse cazuri din domeniu.
Pentru comoditatea
calculelor s-a ales ca variabila independenta unghiul ![]() de rotatie al camei,
asa ca variabilele dependente, figurate in ordonatele sistemelor de axe sunt
pulsul redus
de rotatie al camei,
asa ca variabilele dependente, figurate in ordonatele sistemelor de axe sunt
pulsul redus 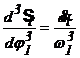 , acceleratia redusa
, acceleratia redusa 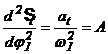 , viteza redusa
, viteza redusa ![]() si spatiul liniar
si spatiul liniar ![]() (sau cel unghiular in
cazul tachetului cu miscare de oscilatie). Toate variabilele dependente au ca
unitate de masura lungimea (sau unghiul in cazul tachetului oscilant).
(sau cel unghiular in
cazul tachetului cu miscare de oscilatie). Toate variabilele dependente au ca
unitate de masura lungimea (sau unghiul in cazul tachetului oscilant).
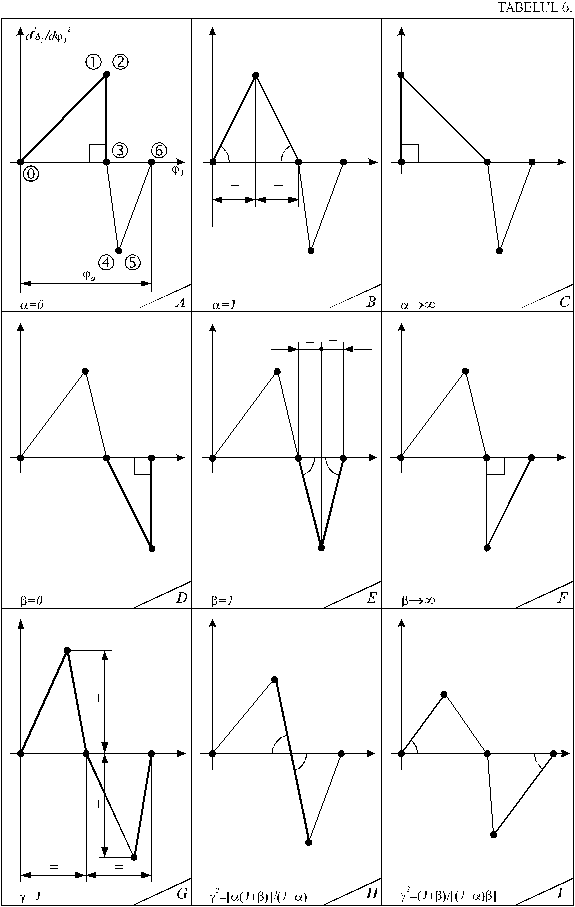
1. Legi de miscare cu pulsul redus 4-constant.
Tabelul 2.
|
|
|
Se utilizeaza relatii pentru coeficientii adimensionali "k" de tipul:
Conditii necesare pentru acceleratii:
|
Particularizand
legea cu pulsul redus constant pe 6 intervale (tabelul 2) se obtine legea cu
pulsul redus constant pe 4 intervale, denumita prescurtat lege cu pulsul redus
4-constant. Intervalele (punctele) intre care variaza acceleratia redusa,
derivate din legea cu puls 6-constant, sunt ![]() ,
, ![]() ,
, ![]() ,
, ![]() (tabelul 3).
(tabelul 3).
Tabelul 3.
|
LEGE
DE VARIATIE CU PULSUL |
|||||||
|
|
|||||||
|
Particularizari si notatii introduse pentru legea de variatie cu pulsul constant pe 4 intervale. | |||||||
|
|
|
|
|
||||
|
|
|
|
|||||
Particularizarile
care conduc la acest tip de lege, in consecinta, sunt in numar de patru: ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Pentru comoditatea calculelor, se
introduc parametrii adimensionali ![]() ,
, ![]() si
si ![]() definiti in tabelul
2. Acestia pot lua valori intre zero si infinit (inclusiv extremele), iar
definiti in tabelul
2. Acestia pot lua valori intre zero si infinit (inclusiv extremele), iar ![]() si
si ![]() sunt strict pozitivi.
sunt strict pozitivi.
Dintre cei 5
parametrii (3 parametrii adimensionali ![]() ,
, ![]() si
si ![]() si 2 parametrii
dimensionali
si 2 parametrii
dimensionali ![]() si
si ![]() ), doar doi sunt dependenti, restul de trei trebuind sa fie
alesi sau corelationati.
), doar doi sunt dependenti, restul de trei trebuind sa fie
alesi sau corelationati.
Datele de intrare la
ridicarea tachetului pentru o lege de variatie cu puls 4-constant sunt: ![]() , h,
, h, ![]() ,
, ![]() ,
, ![]() ,
, ![]() si
si ![]() .
.
Metodologia de calcul este urmatoarea:
Cunoscandu-se ![]() si h se aleg 3
dintre cei 5 parametrii (
si h se aleg 3
dintre cei 5 parametrii (![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ).
).
Se
calculeaza parametrii de tip k si A, precum si coeficientul adimensional
auxiliar ![]() , cu relatiile din tabelul 4.
, cu relatiile din tabelul 4.
Se verifica parametrii k si A cu relatiile din tabelul
Se calculeaza coordonatele (ordonatele) capetelor de interval cu relatiile din tabelul 4.
Se calculeaza intr-un numar convenabil de puncte, ordonatele acceleratiei reduse, vitezei reduse si spatiului, pentru fiecare dintre cele 4 intervale, cu relatiile din tabelul
Se introduc in ecuatiile din tabelul 5 abscisele capetelor de interval, determinate conform diagramei din tabelul 4. Se obtin ordonatele capetelor de interval, care vor trebui sa fie aceleasi cu cele calculate conform tabelului 4.
Pentru ![]() , respectiv
, respectiv ![]() , in relatiile din tabelele 4 si 5 se vor efectua mai intai
trecerile la limita necesare. Se observa ca, spre deosebire de
, in relatiile din tabelele 4 si 5 se vor efectua mai intai
trecerile la limita necesare. Se observa ca, spre deosebire de ![]() si
si ![]() ,
, ![]() nu poate lua valorile
extreme zero sau infinit.
nu poate lua valorile
extreme zero sau infinit.
Anumite particularizari ale parametrilor adimensionali, conduc uneori la introducerea unor salturi finite ale acceleratiei reduse, astfel ca ecuatiile de acceleratii, viteze si spatiu pe acele intervale nu-si mai au sens.
2.
Particularizari ale parametrilor adimensionali ![]() ,
, ![]() si
si ![]() .
.
Pentru legea de variatie a acceleratiilor cu pulsul redus 4-constant, se prezinta o serie de particularizari asupra parametrilor adimensionali, care sunt indicatii de proiectare.
Particularizarile constau fie in alegerea
specifica a valorilor lui ![]() ,
, ![]() si
si ![]() din multimea , fie din stabilirea unor corelatii
specifice intre
din multimea , fie din stabilirea unor corelatii
specifice intre ![]() ,
, ![]() si
si ![]() (tabelele 6, 7).
(tabelele 6, 7).
Cazurile H si I ale
particularizarilor din tabelul 6 sunt implicate de egalitatea pantei dreptei ce
reprezinta acceleratia redusa pe intervalul ![]() cu cea de pe
intervalul
cu cea de pe
intervalul ![]() , respectiv dreapta de pe intervalul
, respectiv dreapta de pe intervalul ![]() cu cea de pe
intervalul
cu cea de pe
intervalul ![]() .
.
Particularizarile din tabelele 6 si 7 sunt restrictii suplimentare asupra datelor de intrare. Aceste doua tabele nu epuizeaza decat cele mai utile particularizari. Unele din aceste particularizari-restrictii (tabelul 7) pot actiona si simultan.
TABELUL 4.
|
|
|||||||||||||||
|
Formulele parametrilor de tip k si A | |||||||||||||||
|
|
|
|
|
||||||||||||
|
|
| ||||||||||||||
|
|
|
|
| ||||||||||||
|
|
|
|
| ||||||||||||
|
|
|
|
|
| |||||||||||
TABELUL 4 - CONTINUARE
|
Pct. |
Coordonatele capetelor de intervale (ordonatele) | ||||
|
|
|
|
|||
|
s |
|
|
|
||
|
|
|
|
|||
|
s |
|
|
|
||
|
|
|
|
|||
|
Politica de confidentialitate |
| Copyright ©
2024 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |