Angrenaje conice concurente
Transmit miscarea de rotatie intre arbori a caror axe se
intersecteaza inchizind intre ele un unghi ![]() .Rotile angrenajului au forma conica si
de aceea angrenajele se numesc conice.
.Rotile angrenajului au forma conica si
de aceea angrenajele se numesc conice.
Suprafete si cercuri de rostogolire
Suprafetele de rostogolire sunt doua conuri care au virful comun in punctul de intersectie O a celor doua axe si sunt tangente de-a lungul generatoarei OP (fig.nr.1).
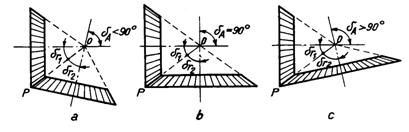
Fig.1
Din figura rezulta: ![]() (1)
(1)
Unde ![]()
![]() sunt semiunghiurile conurilor de rostogolire. Unghiul
dintre axe
sunt semiunghiurile conurilor de rostogolire. Unghiul
dintre axe ![]() poate fi mai mic,egal sau mai mare decit 900.
poate fi mai mic,egal sau mai mare decit 900.
Prezinta interes un caz special
cind conul de rostogolire al unei roti devine un disc -![]() (fig.nr.2).
(fig.nr.2).
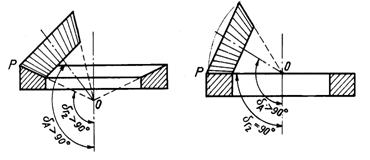
Fig.2
Angrenajul poarta numele de angrenaj cu roata plana. Datorita formei sale angrenajul conic poate fi introdus intr-o sfera (fig.3).
In planele ![]() si
si![]() perpendiculare pe axele conurilor se disting doua
cercuri cu centrele in
perpendiculare pe axele conurilor se disting doua
cercuri cu centrele in ![]() si
si ![]() si de raze
si de raze ![]() si
si ![]() numite cercuri de rostogolire iar punctul P punctul de rostogolire sau polul angrenarii. Conform
figurii se poate scrie:
numite cercuri de rostogolire iar punctul P punctul de rostogolire sau polul angrenarii. Conform
figurii se poate scrie:
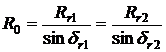
Raportul de transmitere
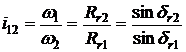
In cazul angrenajului zero si zero deplasat conurile de rostogolire coincid cu cele de divizare si prin urmare:
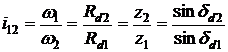
unde ![]() si
si ![]() sunt semiunghiurile conurilor de divizare. Intrucit
sunt semiunghiurile conurilor de divizare. Intrucit
![]() , scriind
, scriind ![]() si inlocuind in ( ) se obtine:
si inlocuind in ( ) se obtine:
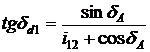
In mod similar se obtine:
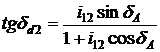
![]()
Pentru angrenajul
ortogonal (![]() ) se obtine:
) se obtine:
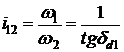 , respectiv
, respectiv 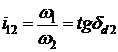
Fie angrenajul conic introdus intr-o sfera (fig.4)
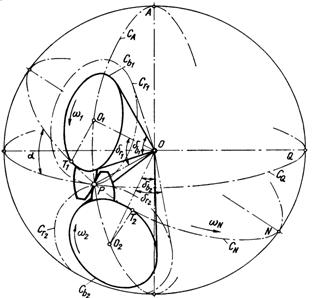
Fig.4
Se disting cercurile mari pe sfera A-A pe care se afla centrele bazelor conurilor de rostogolire a rotilor O1 respectiv O2. Cercurile de baza corespunzatoare celor doua conuri de rostogolire(CT1,CT2) sunt tangente in polul angrenarii P. Se disting si conurile de baza Cb1,Cb2 la care este simultan tangent in punctele T1 respectiv T2 planul N-N descris de cercul mare de pe sfera CN . Rostogolind fara alunecare planul N-N peste unul din conurile de baza, un punct al acestuia descrie pe sfera o evolventa sferica. Situatia se repeta si la raze mai mici astfel incit se poate determina o suprafata infasuratoarea acestor evolvente sferice care constituie flancul dintelui rotii conice.
Roata plana de referinta. Roata plana generatoare
Pentru a putea genera evolventa sferica cu ajutorul unei roti plane, prin analogie cu generarea evolventei plane cu profilul de referinta, trebuie mai intii definita forma evolventei sferice cind una din roti, de exemplu roata 2, devine o roata plana. In acest caz, cercul de rostogolire Cr2 se confunda cu cercul CQ, iar cercul de baza Cb2 (C'b2) devine paralel cu CQ (fig.5). Prin P si O se duce planul auxiliar N' perpendicular pe planul N, care determina pe sfera cercul C'N. Cercul C'N intersecteaza cercurile Cb2 si C'b2 in punctele A si A' .
Evolventa sferica pentru roata plana va fi descrisa de punctul P al arcului T2 T2' cind acesta se rostogoleste fara alunecare, ca in figura ( ), pe cercul Cb2 sau pe C'b2
Din triunghiul dreptunghic sferic APT2, stiind ca ipotenuza AT2 este mai mare decit cateta PT2, se deduce ca la rostogolirea arcului PT2 pe cercul Cb2, punctul P ajunge in B, astfel incit AT2 >BT2 . La fel pentru triunghiul PT'2A' se poate deduce ca A'T'2 > B'T'2
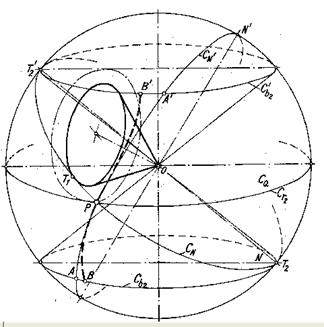
Fig.5
Prin urmare, profilul BB' al dintelui rotii plane se compune din doua arce de evolventa sferica avind curburi contrare, racordate in punctul P. Capul dintelui corespunde unei danturi interioare, iar piciorul - unei danturi exterioare (fig5).
Materializarea flancului dintelui rotii plane cu profil de evolventa sferica prin muchii aschietoare, in vederea prelucrarii prin rulare a rotilor conice, este foarte dificila. Faptul acesta a determinat inlocuirea profilului de evolventa sferica a dintelui rotii pla ne printr-un profil rectiliniu, usor de realizat practic (fig.6.b) Inlocuirea de profil atrage dupa sine o transformare a liniei de angrenare. Linia de angrenare devine dintr-un cerc mare al sferei o curba numita lemniscata sferica asa cum se poate arata usor aplicind constructia lui Reuleux pentru determinarea liniei de angrenare ( figura 7)
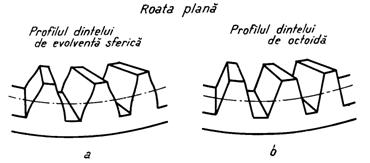
Fig.6
Dantura rotilor se numeste octoidala, datorita formei de opt a liniei de angrenare.(fig.7)
Doua roti dintate cu dantura octoidala angreneaza corect din punct de vedere teoretic atit timp cit liniile lor de angrenare (cele doua lemniscate sferice) se suprapun perfect. Aceasta se intixpla daca conurile de divizare coincid cu conurile de rostogolire.
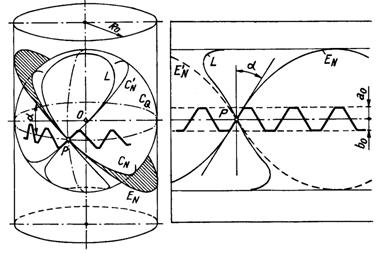
Fig.7
Prin urmare, aceste angrenaje sint sensibile la modificarea unghiului dintre axe. Din aceasta cauza angrenajele conice se realizeaza practic numai sub forma angrenajelor zero sau zero deplasate.
Studiul rotii plane eu modificarile aduse mai sus, prezinta inca dificultati din cauza suprafetei sferice pe care este trasat profilul, deoarece suprafata sferica nu se poate desfasura in plan.Tredgold a introdus o aproximatie,inlocuind suprafata sferica,pe care apare profilul dintilor rotii plane, cu un cilindru frontal (suplimentar) tangent la sfera dupa cercul CQ, deci cu aceeasi raza cu sfera (fig.19.8).Profilul rectiliniu al dintelui danturii octoidale a rotii plane este pe sfera un segment din cercul C'N care rezulta din intersectia sferei cu planul ce trece prin centrul sferei si este perpendicular pe planul cercului CN. Din intersectia acestui plan cu cilindrul frontal rezulta o elipsa EN' tot asa cum se obtine o elipsa EN pentru cercul CN.Desfasurind cilindrul frontal, elipsa E'N devine o sinusoida sl astfel profilul dintelui pe cilindrul frontal este un aegment dintr-o sinusoida.
Cum inaltimea dintelui in raport cu amplitudinea sinusoidei este mica se poate inlocui,in acest interval, cu o precizie satisfacatoare, segmentul de sinusoida cu un segment de dreapta. La fel, in zona delimitata de inaltimea dintelui, lemniscata L si cercul CN se suprapun in masura suficienta pentru ca, fara a face o eroare prea mare, sa se inlocuiasca in final curbele L si E de pe desfasurata cilindrului frontal cu un segment de dreapta. Astfel rezulta pe desfasurata cilindrului frontal o cremaliera similara cremalierei angrenajelor cilindrice.
Roata plana cu dantura octoidala avind aceeasi proprietate ca si cremaliera angrenajelor cilindrice (daca doua roti conice angreneaza separat cu o aceeasi roata plana, angreneaza si intre ele,putind forma deci un angrenaj) este folosita pentru definirea danturilor conice, sub forma rotii plane de referinta.
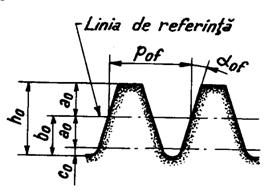
Fig.8
Elementele geometrice ale rotii plane de referinta sint precizate in STAS 6844-63. In figura 8 este redat profilul dintelui rotii plane de referinta de pe cilindrul exterior desfasurat in plan, iar in figura 9 sectiunile axiala si transversala a rotilor plane de referinta cu dinti drepti ei cu dinti inclinati.
Prin analogie cu angrenajele cilindrice, linia profilului rotii plane de referinta pe care grosimea dintelui este egala cu largimea golului si fata de care se masoara inaltimea capului si piciorului
dintelui, ae numeste linie de referinta (fig.8).
Planul care contine linia de referinta si este perpendicular pe axa rotii plane constituie planul de referinta (fig.9)
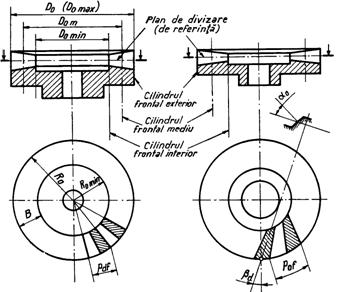
Fig.9
Marimile normalizate ale rotii plane de referinta sint aceleasi ca si la cremaliera angrenajelor cilindrice. Roata plana fictiva care se potriveste in roata plana de refe rinta - capul dintelui uneia corespunzind piciorului dintelui celeilalte si invers - este roata plana generatoare.
Angrenajul echivalent.
Dificultatile studiului geometriei sl cinematicii angrenajelor conice pe o suprafata sferica au impus o metoda aproximativa de profilare a dintilor rotilor conice. Se observa ca suprafetele frontale ale dintilor situate intre cercurile de virf si de fund, formeaza pe sfera niste zone sferice .
Deoarece latimea acestor zone sferice este extrem de mica in comparatie cu raza RQ a sferei pe oare se gasesc, zonele sferice se pot inlocui, cu o precizie satisfacatoare, prin niste trunchiuri de con tangente la sfera in punctele apartinind cercurilor Cd1 si Cd2 (aproximatia lui Tredgold).
Daca cele doua conuri de divizare se reprezinta prin proiectiile lor pe planele care contin axele acestor conuri (triunghiurile OAP si OPB , figura 10), conurile pe suprafetele carora se vor gasi suprafetele frontale ale dintilor pot fi construite in modul urmator:
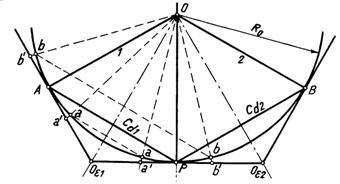
Fig.10
Se proiecteaza conurile de virf si de fund ale rotii l, rezultind triunghiurile bOb si respectiv aOa. In cazul profilarii exacte a dintilor suprafata frontala se proiecteaza pe planele considerate sub
forma unor arce de cerc ab, situate pe proiectiile sferei de raza RQ.
Deoarece
conurile pe care trebuie sa se gaseasca suprafetele
frontale aproximative ale dintilor trebuie sa fie tangente la
sfera dupa cercurile de divizare, pentru determinarea
proiectiilor acestor conuri, se duc din punctele A, P si B
perpendiculare pe razele OA, OP si respectiv OB. La intersectia cu
axele rotilor se obtin punctele 0e si Oe care sint virfurile conurilor cautate.
Proiectia conului rotii l este triunghiul APOe , iar proiectia conului
rotii 2, triunghiul BPOe ![]() .
.
Sectiunile corespunzatoare partilor frontale ale danturii se proiecteaza prin segmentele a' b' care se gasesc pe laturile triunghiurilor construite. Este usor de observat ca cu cit raportul dintre raza sferei si modulul danturii este mai mare, cu atit eroarea ce se comite inlocuind forma sferica a suprafetei frontale a dintilor prin-tr-un trunchi de con va fi mai mica. Conurile cu virfurile in e si Oe se numesc conuri frontale sau suplimentare. Constructia profilelor suprafetelor frontale ale dintilor se poate face acum cu aceleasi procedee ca si in cazul rotilor dintate cilindrice, deoarece conurile frontale se pot desfasura in plan.
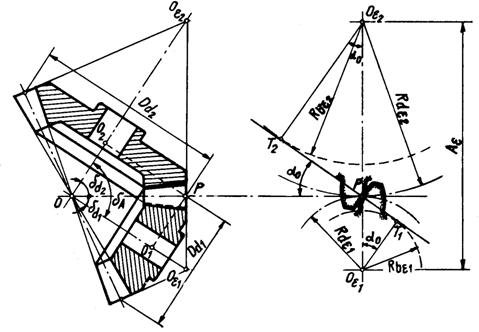
Fig.11
Desfasurind aceste conuri si construind pe cercurile de raze 0e P si Oe P profilele dintilor, in acelasi mod ca la rotile cilindrice, se obtine un angrenaj cilindric paralel, care este angrenajul echivalent al angrenajului conic (fig.11).
Angrenajul echivalent are dantura dreapta sau inclinata, corespunzator danturii angrenajului conic. Elementele angrenajului echivalent cu dantura inclinata ae numesc elemente frontale.
Intrucit la o roata dintata conica marimea razei de divizare depinde de pozitia punctului P pe generatoarea de divizare, rezulta ca ae pot construi o infinitate de angrenaje echivalente (exterior, interior, mediu etc.). Dantura angrenajului echivalent are acelasi pas (modul) ca si angrenajul conic pe cercurile de divizare care sint bazele conurilor frontale desfasurate. Pentru a evita eventualele confuzii, se indica totdeauna modulul maxim m pentru angrenajul cu dantura dreapta - cel standardizat - sl modulul maxim frontal m^ pentru angrenajul cu dantura inclinata.
Cu precizarile de mai sus, se calculeaza elementele angrenajului echivalent, in baza relatiilor stabilite pentru angrenajele cilindrice. Altfel, din triunghiurile O1POe si O2POe (fig.19.3) rezulta razele de divizare echivalente:
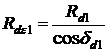 ;
; 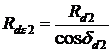
Exprimind razele de divizare Rd ale rotilor angrenajului conic in functie de modulul maxim si de numerele da dinti, razele de divizare echivalente devin:
![]()
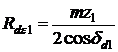 ;
; 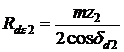
Angrenajul echivalent avind acelasi modul ca si angrenajul conic se poate scrie:
![]() ;
; ![]()
unde ze si ze sint numerele de dinti ai rotilor dintate echivalente. Din relatiile ( ) si ( ) rezulta:
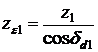 ;
; 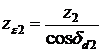
Raportul de transmitere al angrenajului echivalent este:
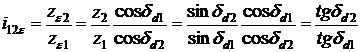
care in cazul angrenajului conic ortogonal devine:
![]()
Razele cercurilor de baza echivalente sunt:
![]() ;
; ![]()
![]()
pentru angrenajul conic cu dantura
dreapta si![]()
![]()
![]()
in cazul angrenajului conic cu dantura inclinata sau curba.
Distanta dintre axele angrenajului echivalent rezulta ca suma a razelor de divizare echivalente
![]()
Calculul geometric al angrenajului conic cu dantura dreapta
Calculul geometric are drept scop determinarea marimilor geometrice necesare pentru realizarea angrenajului, a unor marimi pentru verificarea dimensionala si a unor coeficienti de calitate ai angrenajului, cum sunt gradul de acoperire si ascutirea dintilor. Acest calcul se efectueaza pe baza marimilor normalizate ale rotii plane (m, a , f0 si w0 ), a parametrilor principali ai angrenajului ( dA , z1, z2, x si x ) avind in vedere clasa de precizie a acestuia.
Calculul geometric al angrenajului se executa dupa ce, in prealabil, se face un calcul de rezistenta pentru determinarea modulului maxim. In paralel cu determinarea modulului, rezulta latimea danturii B si numerele de dinti z1 si z2, care permit alegerea deplasarilor specifice ale profilelor x si x In functie de clasa de precizie se stabilesc tolerantele angrenajului si se calculeaza marimile necesare controlului dimensional.
La alegerea rotii plane de referinta trebuie sa se tina sema de particularitatile masinii pe care se va realiza dantura. Se prefera unghiul de referinta a = 2o°. Sint insa si masini (Gleason) la care se poate folosi unghiul de angrenare a = 14°30'. Coeficientul de inaltime a capului dintelui se ia de obicei f0 =1, iar coeficientul jocului la capul dintelui depinde de tipul masinii de danturat. De exemplu , w0 = 0,188 pentru masinile Gleason si w0 = 0,1236 in cazul masinilor Heidenreich - Harbeck, Bilgram si Reinecker.
Modificarea danturii conice.
Modificarea danturii angrenajului conic este impusa in general de aceleasi cauze ca si la angrenajul cilindric, cu exceptia realizarii unei distante dintre axe date.Datorita particularitatilor tehnologice a generarii danturii conice,( de regula cu scule independente pentru cele doua flancuri ale dintelui), la dantura conica se disting doua feluri de deplasari ale profilului: deplasare radiala si deplasare tangentiala.
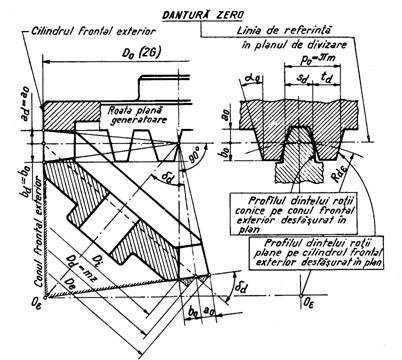
1°. Deplasarea radiala a profilului. S-a aratat in capitolul precedent ca profilul dintelui rotii conice de pe conul frontal (suplimentar) exterior desfasurat in plan este aproximativ identic cu profilul unei roti dintate cilindrice evolventice, care are raza de divizare egala cu lungimea generatoarei conului frontal (fig.7). De asemenea, profilul dintelui rotii plane pe cilindrul frontal exterior corespunde cremalierei de referinta a rotilor dintate cilindrice (figura12).
Daca profilul dintelui rotii plane generatoare pe cilindrul frontal exterior este asezat in asa fel incit linia de referinta a profilului este cuprinsa in planul de divizare al rotii plane (fig.12 ), se genereaza o dantura conica zero.
In acest caz rezulta ca:
- inaltimea capului de divizare a dintelui si cea a piciorului dintelui sint respectiv egale cu cele de referinta:
![]() ;
; ![]()
-diametrul de virf al rotii este:
![]()
-iar diametrul de fund:
![]()
- arcul de divizare al dintelui (arcul dintelui) este egal cu arcul de divizare al golului (arcul golului) si egal cu jumatatea pasului de referinta:
![]()
Dantura conica cu profil deplasat ia nastere atunci cind linia de referinta a profilului rotii plane pe cilindrul frontal exterior este deplasata fata de planul de divizare. In cazul unei deplasari pozitive (fig.2o.2) rezulta :
inaltimea capului de divizare a dintelui
![]()
si inaltimea piciorului de divizare
![]()
diametrul de virf al rotii deplasate este
![]()
iar diametrul de fund
![]()
arcul dintelui sd este diferit de arcul golului td si are valoarea
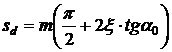
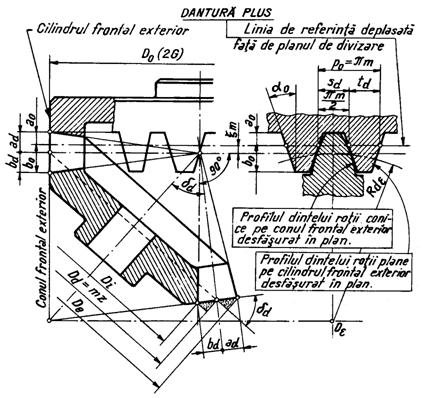
Fig.13
Deplasarea tangentiala a profilului.
Aceasta deplasare consta in mutarea laterala a unuia din flancurile dintilor rotii plane generatoare. Astfel, prin deplasarea laterala a flancului intr-un sens (fig.12,a), dintele devine mai gros decit cel nedeplasat, iar prin deplasarea in sens contrar (fig.12,b), dintele devine mai subtire.
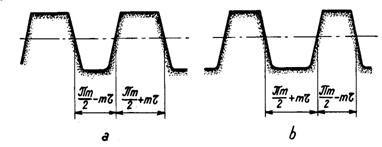
Fig.12
Ca doua roti conice sa poata angrena, fara modificarea unghiului dintre axe, este necesar ca deplasarea tangentiala pozitiva (care duce la ingrosarea dintelui) a unei roti conice sa fie riguros egala cu deplasarea tengentiala negativa (care duce la subtierea dintelui) a rotii conice conjugate. De obicei deplasarea tangentiala pozitiva se aplica rotii cu numar de dinti mai mic (pinionului).
Prin deplasarea tangentiala a profilului, se muta profilul dintelui, dar el ramine neschimbat ca forma, in timp ce la deplasarea radiala se foloseste o alta portiune a evolventei (respectiv a profilului octoidal). De aceea deplasarea tangentiala poate imbunatati numai rezistenta la incovoiere a dintilor dar nu schimba nimic in conditiile geometrice ale angrenajului (subtaiere, interferenta, grad de acoperire, ascutire etc.).
Deplasarea tangentiala a profilului se aplica si in cazul cind nu se face o deplasare radiala. De exemplu, folosind materiale diferite pentru pinion si roata, se pot realiza danturi de aceeasi rezistenta la incovoiere.
Citeodata, se aplica simultan deplasarea radiala si tangentiala a profilului, realizindu-se o dantura imbunatatita din mai multe puncte de vedere. In cazul in care se aplica danturii atit o deplasare radiala cit si o deplasare tangentiala, arcul de divizare al dintelui devine:
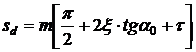
unde prin t s-a notat deplasarea tangentiala specifica.
Modificarea danturii rotilor dintate conice poate fi realizata si prin modificarea unghiului de referinta al rotii plane.
Numarul de dinti ai pinionului
Stabilirea numarului de dinti ai pinionului se poate face dupa criteriul evitarii subtaierii. Numarul minim de dinti care asigura prelucrarea fara subtaiere a unei danturi zero se stabileste pe baza angrenajului echivalent, in functie de numarul de dinti echivalent. Conform teoriei angrenajelor cilindrice cu dantura exterioara dreapta, numarul minim de dinti care ce poate admite in cazul danturilor zero cu evitarea subtaierii este
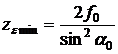
Pentru unghiul de referinta a = 20° si f0 = l se se obtine zemin = 17. In practica se admite zemin = 14, avind in vedere ca si la acest numar de dinti subtaierea inca nu este suparatoare.
Tinind seama de relatia ( ) rezulta numarul minim de dinti realizabil fara subtaiere la o dantura conica dreapta nedeplasata.
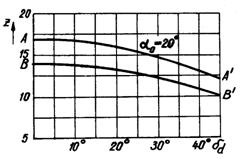
Fig.13
![]() (teoretic) ;
(teoretic) ; ![]() (practic)
(practic)
In figura 13 este data variatia numarului minim de dinti in functie de semiunghiul conului de divizare dd Curba AA' reprezinta cazul teoretic, iar curba BB' cazul admis inca in practica. Deci, daca numarul de dinti z ales se afla pe linia AA' sau deasupra acestei linii se poate realiza o dantura zero. Daca numarul de dinti z se afla sub linia BB', pinionul nu poate fi prelucrat ca pinion zero decit cu subtaiere, pentru evitarea careia trebuie sa se aplice profilului o deplasare pozitiva.
Deplasarea minima pentru evitarea subtaierii, conform teoriei angrenajelor cilindrice cu dantura exterioara dreapta este
![]() (teoretic);
(teoretic); 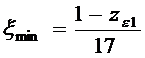 (practic)
(practic)
valoare ce poate fi determinata direct pe baza nomogramei (), in functie de ze
Prin deplasarea pozitiva a profilului se micsoreaza arcul dintelui pe cercul de virf. Deplasarea specifica pozitiva a profilului pentru care arcul dintelui pe cercul de virf are o anumita valoare, rezulta din nomograma din fig.13, in functie de numarul echivalent de dinti. In mod practic, arcul dintelui pe cercul de virf trebuie sa fie se > 0,25 m.Asa cum s-a aratat, angrenajele conice se realizeaza in general sub forma angrenajelor zero si zero deplasate. Conform teoriei angrenajelor cilindrice, pentru realizarea unui angrenaj conic zero deplasat trebuie indeplinita conditia
![]()
care cu luarea in considerare a relatiilor (19.2o) devine:
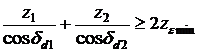
sau
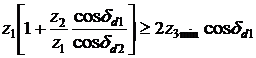
In cazul angrenajului ortogonal conditia devine
![]()
La alegerea numarului de dinti ai pinionului trebuie avute in vedere insa atit conditiile tehnologice cit si conditiile de rezistenta si de durabilitate a angrenajului. Pe baza experientei acumulate firmele producatoare de masini de danturat au intocmit recomandari pentru alegerea numarului de dinti ai pinionului, cit si pentru deplasarile specifice ale profilului.
Firma Gleason recomanda utilizarea valorilor din tabelul l pentru numarul de dinti ai pinionului, in cazul cind se utilizeaza sistemul de deplasari propus de fabrica, redat in tab. 3
G. Niemann recomanda sa se aleaga numarul minim de dinti ai pinionului conform tabelului 2, atit pentru dantura dreapta cit si pentru dantura curba
Numarul minim de dinti pentru dantura dreapta (dupa Gleason)
|
Unghiul de angrenare a |
Numarul de dinti ai pinionului Z1 |
Numarul minim de dinti ai rotii Z2 |
Raportul de transmitere minim i12 min |
|
2o° |
3o | ||
|
2o | |||
|
l,oo |
|||
|
14°3o' | |||
|
4o |
l,6o |
||
|
l,oo |
G. Niemann recomanda sa se aleaga numarul minim de dinti ai pinionului conform tabelului 2, atit pentru dantura dreapta cit si pentru dantura curba.
Tabelul 2
Numarul de dinti ai pinionului (dupa G. Nieman)
|
Raportul de transmitere i12 | ||||||
|
Numarul minim de dinti z1 |
15 3o | |||||
|
. Se recomanda sa se admita z1 la limita superioara in cazul rotilor conice cu dantura dreapta si cu flancuri moi sau semidure, si la limita inferioara in cazul rotilor cu dinti curbi si flancuri dure. De asemenea, la stabilirea numarului de dinti ai pinionului se poate avea in vedere numarul critic de dinti-vezi relatia ( ) |
||||||
Sisteme de deplasari specifice.
In ceea ce priveste deplasarile specifice ale profilului, firma Gleason recomanda numai deplasari radiale plus pentru pinion si deplasari minus de aceeasi valoare pentru roata, stabilite astfel incit rezistenta la incovoiere a dintelui rotii si pinionului aa aiba aceeasi valoare (tabelul.3).
Tabelul3
Deplasarile ![]() pentru
pentru ![]() ,
, ![]() si dantura dreapta (dupa Gleason)
si dantura dreapta (dupa Gleason)
|
Raportul de transmitere i12 |
x |
Raportul de transmitere i12 |
x |
Raportul de transmitere i12 |
x |
|
1.00. .1,02 1,02. .1,03 1,03. .1,04 1,04. -I,05 1,05. .1,06 1,06. .1,08 1,08. .I,09 1,09. .1,11 1,11. .1,12 1,12. .1,14 1,14. .1,15 1,15. .1,17 1,17. .1,19 1,19. .1,21 1,21. .1,23 |
1,23. .1,25 1,25. .1,27 1,27. .1,29 1,29. .1,31 1,31. .1,33 1,33. .1,36 1,36. .1,39 1,39. .1,42 1,42. .1,45 1,45. .1,48 1,48. .1,52 1,52. .1,56 1,56. .l,6o l,6o. .1,65 1,65. .l,7o l,7o. .1,76 |
0,16 0,17 0,18 0,19 0,20 0,21 0,22 0,23 0,24 0,25 0,26 0,27 0,28 0,29 0,3o 0,31 |
1,76. .1,82 1,82. .1,89 1,89. .1,97 1,97. .2,o6 2,06. .2,16 2,16. .2,27 2,27. .2,41 2,41. .2,58 2,58. .2,78 2,78. .3,o5 3,05. .3,41 3,41. .3,94 3,94. .4,82 4,82. .6,81 6,81. . |
0,4o |
|
|
. Daca deplasarii specifice corespunzator raportului de transmitere calculat. |
|||||
|
. Daca |
|||||
Particularitatile jocului la capul dintelui
Dupa felul jocului la capul dintelui angrenajele conice pot fi cu joc la capul dintelui variabil si cu joc la capul dintelui constant.
Jocul la capul dintelui variabil
In cazul angrenajelor cu joc variabil, conurile de divizare, conurile de virf si cele de fund ale ambelor roti au virful comun, in punctul O, de intersectie a axelor (fig.14) Dimensiunile dintilor nu sint aceleasi de-a lungul lor.
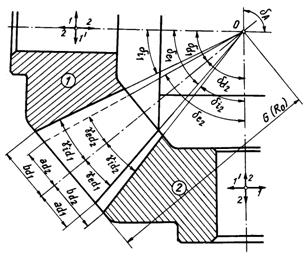
Fig.14
Spre virful conului scade atit inaltimea piciorului dintelui cit si inaltimea capului, in aceeasi proportie scazind si jocul la capul dintelui. Conform figurii 14 rezulta :
unghiul capului de divizare al dintelui
![]() ,
, ![]()
unghiul piciorului de divizare al dintelui
![]() ,
, ![]()
Semiunghiurile conurilor de virf, care sunt necesare la strunjirea rotilor conice
![]() ,
, ![]()
semiunghiurile conurilor de fund, care sunt necesare la montarea rotilor pe masina de danturat
![]() ,
, ![]()
In figura 15 este reprezentata o roata dintata conica a unui angrenaj cu joc la capul dintelui variabil.
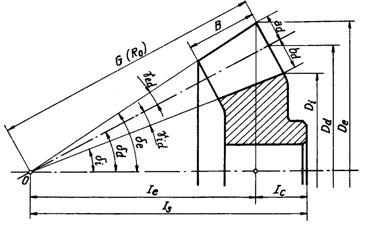
Fig.15
Distanta IS este numita distanta de sprijinire. Relatia pentru calculul acestei marimi rezulta din figura 15:
![]()
![]()
in care distanta Ic se alege constructiv.
Se observa ca pozitia fiecarei roti fata de roata conjugata este determinata in doua directii (fig.15) radiala (sagetile 1) si axiala (sagetile 2). Deplasarile axiale si radiale duc la modificarea jocului la capul dintelui. Daca roata se deplaseaza axial spre punctul de intersectie al axelor sau radial in sensul sagetilor l', jocul se micsoreaza. Deplasarea fiind aceeasi pentru orice punct al rotii, micsorarea jocului de-a lungul dintelui este constanta. Cum jocul initial

Fig.14
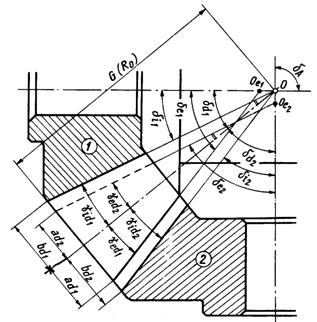
Fig.15
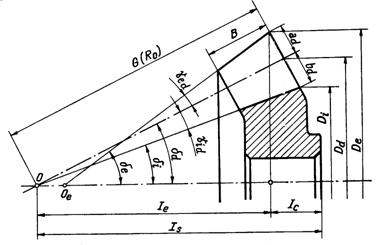
Fig.16
|
Politica de confidentialitate |
| Copyright ©
2024 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |