
SIMILITUDINEA SI ANALIZA DIMENSIONALA
1. Similitudinea
1.1. Aspecte generale
Pentru vizualizarea unor fenomene si procese fizice din domeniul mecanicii fluidelor, obtinerea de rezultate cantitative privind evolutia acestora si, eventual, modificarea ritmului lor de desfasurare, se foloseste modelarea fizica. Aceasta consta din inlocuirea domeniului efectiv de desfasurare a procesului (numit in cele ce urmeaza prototip) cu un domeniu la scara redusa, numit model, in conditiile asigurarii posibilitatii de transpunere a rezultatelor obtinute pe model in cadrul prototipului.
Convertirea rezultatelor experimentale aferente modelului in date caracteristice prototipului se realizeaza prin multiplicarea lor cu coeficienti de scara, definiti ca expresii ale conditiilor de similitudine a modelului cu prototipul.
Conditiile de asemanare a formei frontierelor modelului si prototipului constituie similitudinea geometrica si sunt exprimate prin relatia
![]() (1)
(1)
unde l este lungimea, iar indicii 1, 2 se refera la prototip, respectiv model.
Similitudinea cinematica consta din asigurarea asemanarii geometrice a spectrelor liniilor de curent si a proportionalitatii vitezelor in punctele omoloage ale modelului si prototipului. Similitudinea cinematica o inglobeaza pe cea geometrica atunci cand frontiera domeniului miscarii este formata din linii de curent. Conditia de proportionalitate a vitezelor implica introducerea coeficientului de timp
![]() (2)
(2)
Similitudinea dinamica impune ca, in puncte omoloage, fortele de acelasi tip sa se afle in raport constant, oricare ar fi cele doua puncte omoloage considerate. Coeficientul de scara pentru forta are expresia
![]() (3)
(3)
unde cu fj, j = 1, 2 s-au notat fortele pe unitatea de volum, deci fj = mj aj/Vj = rj aj, iar ecuatia (3) devine
![]() (4)
(4)
indicand faptul ca similitudinea dinamica include similitudinea cinematica daca raportul densitatilor Cr r r (numit coeficient de scara pentru densitate) in puncte omoloage este constant.
Conditia de proportionalitate a fortelor de acelasi tip existente in puncte omoloage poate fi exprimata sub forma conditiei de asemanare a poligonului fortelor (inclusiv forta de inertie) din puncte omoloage.
Deoarece ecuatiile de echilibru si de miscare a fluidelor exprima conditia de inchidere a poligonului fortelor, rezulta ca asemanarea poligonului fortelor in puncte omoloage se traduce prin identitatea ecuatiilor de echilibru, respectiv de miscare, pentru model si prototip.
In general, conditia de similitudine a doua procese (prototip si model), indiferent de natura acestora (procese chimice, mecanice, termice, electrice etc.), consta in identitatea ecuatiilor fizice ale modelului si prototipului.
1.2. Criterii de similitudine
Spre
exemplificare, se considera cazul studierii pe model a miscarii
laminare a unui fluid vascos incompresibil, prezentata din §7.2.1. Conditia
de asigurare a similitudinii dinamice se reduce la identitatea ecuatiilor
(7.10) pentru prototip si model. Inmultind cu r prima ecuatie (7.10), observand ca
termenii 2, 3 si 4 din membrul stang pot fi grupati sub forma ![]() si asociind indicii 1 pentru prototip,
respectiv 2 pentru model, se pot scrie relatiile
si asociind indicii 1 pentru prototip,
respectiv 2 pentru model, se pot scrie relatiile
![]() (5)
(5)
![]() (6)
(6)
Definind coeficientii de
scara si inlocuind marimile din ecuatia (5) cu expresiile; r r Cr, v1 =
v2 Cv, ![]() , X1 = X2 Ca,
p1 = p2 Cp, m m Cm, x1 = x2
Cl, unde Cv
= v1/v2, Ca
= X1/X2 (sau Ca
= g1/g2 in campul gravitational terestru, cand g este acceleratia
gravitationala), Cp
= p1/p2, Cm m m sunt
coeficientii de scara pentru viteza, acceleratie, presiune,
respectiv vascozitate dinamica, se
obtine forma
, X1 = X2 Ca,
p1 = p2 Cp, m m Cm, x1 = x2
Cl, unde Cv
= v1/v2, Ca
= X1/X2 (sau Ca
= g1/g2 in campul gravitational terestru, cand g este acceleratia
gravitationala), Cp
= p1/p2, Cm m m sunt
coeficientii de scara pentru viteza, acceleratie, presiune,
respectiv vascozitate dinamica, se
obtine forma
![]() (7)
(7)
care, identificata cu ecuatia (6), duce la egalitatile
![]() (8)
(8)
Relatiile (8) reprezinta conditiile de similitudine dinamica, care grupate astfel
![]() (9)
(9)
devin, dupa efectuarea simplificarilor si inlocuirea coeficientilor de scara cu expresiile lor de definitie,
![]() (10)
(10)
![]() (11)
(11)
Prima relatie (10) exprima conditia de identitate pe model si prototip a raportului dintre fortele de inertie fij = rjvj/tj si fortele de frecare ffj = mj/lj tj (unde j = 1, 2, iar fortele sunt exprimate pe unitatea de volum), raport cunoscut sub numele de numarul Reynolds
![]() (12)
(12)
A doua relatie (10) exprima identitatea pe model si prototip a numarului Froude
![]() (13)
(13)
definit ca raportul dintre fortele de inertie si fortele gravitationale fgj = rj gj rj lj gj/(vj tj).
Prima relatie (11) cere satisfacerea conditiei de identitate a raportului fortelor de presiune fpj = pj/lj si fortelor de inertie fij = rj vj/tj = rj vj /lj, raport numit numarul Euler
![]() (14)
(14)
A doua relatie (11) reprezinta criteriul de homocronie a miscarilor pe model si prototip, formulat ca o identitate a numarului Strouhal, definit astfel
![]() (15)
(15)
Conditia Sh1 = Sh2 rezulta, de asemenea, din identitatea ecuatiei de continuitate (4.29) pentru model si prototip.
Marimile Re, Fr, Eu, Sh sunt parametri adimensionali, iar relatiile (10) si (11) reprezinta criteriile de similitudine pentru miscarea laminara, exprimate in functie de aceste marimi.
Satisfacerea simultana a mai multor criterii de similitudine este dificila si, in general, se obtine folosind pe model un fluid cu proprietati fizice diferite de cele ale fluidului de pe prototip.
Pentru a elimina aceste dificultati de modelare fizica, se apeleaza la similitudinea restransa, care consta din compararea ponderilor fortelor din sistem, stabilirea celor predominante si formularea criteriilor de similitudine relative la fortele predominante.
In aceste conditii, se observa ca: numarul Reynolds este criteriul de similitudine restransa la cazul in care fortele predominante sunt cele de inertie si de frecare, numarul Froude exprima similitudinea restransa pentru miscarea fluidelor la care sunt predominante fortele de inertie si cele gravitationale, iar numarul Euler corespunde similitudinii restranse in cazul preponderentei fortelor de presiune si a fortelor de inertie.
Criteriile de similitudine restransa pot fi stabilite si pe baza egalitatii rapoartelor fortelor de acelasi tip, de pe model si prototip.
Daca fortele de inertie fij = rj vj /lj si cele interfaciale (sau superficiale) fin j = sj/lj2, j = 1, 2, sunt predominante, scriind egalitatea rapoartelor lor pe prototip si model
![]() (16)
(16)
se ajunge la relatia
![]() (17)
(17)
care mai poate fi scrisa sub forma
We1 = We2 , (18)
in care
![]() (19)
(19)
este numarul Weber, definit ca raport intre fortele de inertie si cele interfaciale, iar s reprezinta tensiunea interfaciala sau, dupa caz, cea superficiala.
Numarul Mach reprezinta radacina patrata a raportului fortelor de compresibilitate si de inertie, avand expresia
![]() (20)
(20)
unde v este viteza fluidului compresibil, iar c - viteza sunetului in fluidul respectiv. Identitatea acestui numar in doua puncte omoloage de pe model si prototip constituie criteriul Mach, care reprezinta conditia de similitudine restransa in cazul in care fortele de compresibilitate si fortele de inertie sunt predominante. Tinand seama ca forta de compresibilitate raportata la volum are expresia
![]() (21)
(21)
care, in baza relatiei (2.35), devine
![]() (22)
(22)
din egalitatea
![]() (23)
(23)
rezulta identitatea
![]() (24)
(24)
folosita sub forma
![]() (25)
(25)
si cunoscuta sub numele de criteriul Mach.
Unele dintre numerele prezentate in acest paragraf stau la baza delimitarii unor tipuri de miscari. Astfel: numarul Reynolds se foloseste pentru a se preciza daca miscarea lichidelor vascoase in conducte este laminara sau turbulenta, numarul Froude delimiteaza, pe baza valorii critice unu, miscarea lenta de miscarea rapida in canale, iar numarul Mach sta la baza clasificarii miscarii gazelor.
2. Analiza dimensionala
2.1. Legea omogenitatii dimensionale
Legea omogenitatii dimensionale se enunta astfel: orice ecuatie obtinuta analitic pentru un fenomen fizic este valabila indiferent de sistemul de unitati de masura considerat. O confirmare plauzibila a acestei legi o constituie faptul ca fenomenele naturale se desfasoara total independent de unitatile de masura concepute de om si, ca urmare, ecuatiile fundamentale corespunzatoare acestor fenomene trebuie sa aiba valabilitatea asigurata pentru orice sistem de unitati de masura. In acest sens, ecuatiile fundamentale ale fizicii fiind dimensional omogene, toate relatiile care deriva din acestea vor fi dimensional omogene, adica toti termenii ecuatiilor respective vor avea aceeasi reprezentare dimensionala.
Ca urmare a acestei cerinte, pentru trecerea de la un sistem de unitati de masura la altul, fiecare termen al ecuatiei fizice respective este multiplicat cu acelasi factor adimensional. Gratie omogenitatii dimensionale, prin impartirea acestei ecuatii la expresia dimensionala a unui termen, termenii ecuatiei devin adimensionali si se numesc grupuri adimensionale.
Legea omogenitatii dimensionale se utilizeaza pentru stabilirea unitatilor de masura ale marimilor derivate intr-un sistem de unitati de masura.
O alta aplicatie importanta a acestei legi consta in stabilirea relatiei dintre variabilele implicate intr-un fenomen fizic, cand, pe baza unor studii experimentale, au fost precizate variabilele respective. Acest lucru se realizeaza printr-un procedeu numit analiza dimensionala, in cadrul caruia evolutia fenomenului fizic este formulata printr-o relatie intre grupuri adimensionale de variabile, in care numarul grupurilor este mai mic decat numarul variabilelor. Avantajele folosirii acestui procedeu constau atat in reducerea numarului de experimente necesare stabilirii relatiei intre variabilele respective intr-un domeniu dat, cat si in simplificarea acestor experimente.
Numarul parametrilor adimensionali independenti care corespund unui fenomen fizic se determina cu ajutorul teoremei p
2.2. Teorema p
Conform teoremei p, stabilita de E. Buckingham in anul 1915, numarul grupurilor adimensionale independente care pot fi folosite pentru descrierea unui fenomen ce depinde de n variabile este egal cu n-r, unde r este numarul marimilor fundamentale necesare exprimarii dimensionale a variabilelor. In cazul sistemelor de unitati de masura restranse la domeniul mecanicii, numarul marimilor fundamentale este r = 3.
Un fenomen fizic care depinde de variabilele q1, q2,, qn este descris de ecuatia
f(q1, q2,, qn) = 0 . (26)
Daca se aleg ca marimi fundamentale variabilele q1, q2, q3 si se admite ca ele au unitatile de masura variabile si egale cu q1, q2, q3, atunci variabilele q4, q5,, qn pot fi exprimate astfel
![]() (27)
(27)
unde pi este un numar adimensional, iar xi, yi, zi sunt exponenti care vor fi determinati ulterior. Se observa ca relatia (27) este valabila si pentru i = l, 2, 3, rezultand p p p = 1, x1 = y2 = z3 = 1, y1 = z1 = x2 = x3 = y3 = z2 = 0.
Tinand seama de omogenitatea dimensionala a ecuatiei (26) si de marimile fundamentale alese, ecuatia (26) este echivalenta cu relatia
f1(p p pn , (28)
care se conformeaza teoremei p si are pentru parametrii adimensionali expresia rezultata din formula (27) transcrisa astfel
![]() (29)
(29)
Exponentii xi, yi, zi se obtin din ecuatia de dimensiuni
![]() (30)
(30)
folosind pentru variabile expresia dimensionala definita in cadrul Sistemului International de unitati (SI).
Ecuatia (28) poate fi scrisa sub forma
![]() (31)
(31)
care arata ca, in cazul apelarii la experimente pe model fizic, similitudinea este asigurata prin identitatea ecuatiei (26) pentru model si prototip daca n - 4 parametri adimensionali independenti sunt identici pe model si prototip.
2.3. Aplicatii ale teoremei p
2.3.1. Legea fundamentala a hidrostaticii
Cercetarile experimentale au aratat ca repausul unui lichid incompresibil in camp gravitational este caracterizat printr-o stare de presiune care depinde de densitatea r a lichidului, de acceleratia gravitationala g si de adancimea h.
In aceste conditii, ecuatia (26) ia forma particulara
f(r, g, h, p) = 0 . (32)
Intrucat n = 4 si r = 3, rezulta ca exista un singur parametru adimensional independent care, potrivit relatiei (29), are expresia
![]() (33)
(33)
Din identificarea exponentilor relatiei (30), particularizata astfel
![]()
se obtine sistemul de ecuatii algebrice
x = 1 , -3 x4 + y4 +z4 = -1 , -2 y4 = -2 ,
a carui solutie
x = 1 , y4 = 1 , z4 = 1 ,
introdusa in relatia (33), duce la expresia
![]() (34)
(34)
Pe de alta parte, din ecuatia (31) redusa la forma
![]() (35)
(35)
si identificata cu relatia (34), rezulta formula
![]() (36)
(36)
care, pentru c = l si p = 0 la h = 0 exprima legea fundamentala a hidrostaticii referitoare la presiunea relativa, formulata prin ecuatia (3.39).
2.3.2. Legea rezistentei opuse unui corp la inaintarea sa printr-un fluid
Prin cercetari experimentale s-a stabilit ca rezistenta R opusa de fluid la inaintarea unui corp depinde de densitatea r a fluidului, de viteza v a corpului si de aria maxima A a sectiunii corpului normale pe directia miscarii.
Conform relatiei (29), singurul parametru adimensional independent are expresia
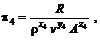 (37)
(37)
in care exponentii x4, y4, z4, rezultati pe baza ecuatiei (30) scrisa sub forma
![]() (38)
(38)
sunt solutia sistemului algebric
![]()
si au valorile x4 = 1, y4 = 2, z4 = 1. Introducand aceste valori in relatia (37) se obtine
![]() (39)
(39)
Ecuatia (31) ia forma particulara (35) care, asociata cu relatia (39), duce la formula
![]() (40)
(40)
unde, in realitate, coeficientul de rezistenta la inaintare C nu este constant, ci depinde de vascozitatea m prin intermediul numarului Reynolds, iar in cazul fluidelor cu vascozitate mica exprima atat efectul frecarii in stratul limita, cat si rezistenta de forma, reflectata prin desprinderea stratului limita.
2.3.3. Legea variatiei efortului tangential la perete in cazul miscarii unui fluid vascos printr-o conducta
Cercetarile experimentale au dovedit ca, in cazul miscarii unui fluid vascos incompresibil printr-o conducta de sectiune circulara, miscarea depinde de densitatea r, viteza medie v, diametrul d, efortul unitar tangential la perete tp si rugozitatea echivalenta k.
In aceste conditii, ecuatia (26) imbraca forma
![]()
careia ii corespunde relatia (31), particularizata astfel
p = F(p p ) , (41)
unde cei trei parametri adimensionali au expresiile
![]() (42)
(42)
Apeland la relatia (29) se pot scrie egalitatile
![]()
![]() (43)
(43)
![]()
care conduc la urmatoarele trei sisteme de ecuatii algebrice
x = 1 , -3 x4 + y4 + z4 = -1 , -y4 = -2 ;
x = 1 , -3 x5 + y5 + z5 = -1 , -y5 = -1 ;
x = 0 , -3 x6 + y6 + z6 = 1 , y6 = 0 ,
ale caror solutii
x = 1 , y4 = 2 , z4 = 0 ,
x = 1 , y5 = 1 , z5 = 1 ,
x = 0 , y6 = 0 , z6 = 1 ,
introduse in expresiile (29) definesc parametrii adimensionali astfel
![]() (44)
(44)
Ca urmare, prin substituirea parametrilor adimensionali in ecuatia (41), se obtine formula efortului unitar tangential la peretele conductei
![]() (45)
(45)
unde
![]() (46)
(46)
si se numeste coeficientul de rezistenta hidraulica al lui Fanning.
3. Probleme
1. O parasuta de forma emisferica, de care este suspendat un colet, coboara spre suprafata solului, in conditii de echilibru dinamic, cu viteza v = 4,5 m/s. Cunoscand: greutatea totala a sistemului parasuta-colet G = 1,2 kN, presiunea si temperatura aerului atmosferic p = 750 torr, respectiv T = 283,15 K, constanta universala a gazelor Ru = 314,3 J/(kmol·K), masa molara a aerului Ma = 28,9 kg/kmol, precum si valoarea coeficientului de rezistenta la inaintare C = 1,33, se cere sa se calculeze diametrul parasutei.
Rezolvare
Forta de rezistenta la inaintare are expresia (40), in care aria emisferei este A = pd /2. Conditia de echilibru dinamic al parasutei implica R = G, deci se poate scrie ecuatia
![]()
din care se exprima diametrul parasutei sub forma
![]()
Densitatea aerului poate fi aflata din ecuatia de stare a gazelor reale
![]()
in care Z 1, deoarece p si T au valori apropiate de cele aferente starii normale.
Se obtin astfel valorile:
![]()
![]()
|
Politica de confidentialitate |
| Copyright ©
2024 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |