
In sistemele tehnologice, coordonarea joaca un rol important la diferite nivele. Rețelele Petri sunt adecvate pentru modelarea și verificarea sistemelor concurente [17],[18],[19].
Sistemele fluxuri de lucruri pot fi modelate de rețele fluxuri de lucru (WF-nets). Acestea sunt rețele Petri cu o locație inițiala și finala, și fiecare locatie intermediara se gaseste pe o cale de la ea pana la cea finala. Efectuarea/execuția unui caz reprezinta o secventa de actiuni ale tranzitiilor, care incepe din marcajul inițial și consta dintr-un singur jeton in locația inițiala. Jetonul din locația finala, fara informații de valoare, lasa in alte locații indicate terminarea adecvata a efectuarii cazului.
Modelul este denumit stabil daca fiecare marcaj accesibil conduce la marcajul final (terminare normala).
Rețele WF sunt modele care furnizeaza ordinea parțiala a activitaților in procese cu resurse, care pot in plus restricționa apariția activitaților. Ca si obiect de analiza se scoate in evidenta influența resurselor in transformarea/prelucrarea cazurilor in rețelele WF. Se iau in considerare doar resurse durabile, care nu pot fi create sau distruse. Rețeaua -RCWF, este o rețea fluxuri de lucru ce conține o rețea/subrețea de producție unde resursele sunt abstractizate, și numarul jetoanelor din locațiile resursa restricționeaza funcționalitatea rețelei de producție.
Un sistem de tranziție este un tuplu ![]() unde S este o
mulțime a pozițiilor/starilor, Act este o mulțime
finita a numelor acțiunii și
unde S este o
mulțime a pozițiilor/starilor, Act este o mulțime
finita a numelor acțiunii și ![]() este o relație de
tranziție.
este o relație de
tranziție.
Un proces este o pereche ![]() unde E este un sistem
de tranziție și
unde E este un sistem
de tranziție și ![]() starea
inițiala. Notam
starea
inițiala. Notam ![]() ca
ca ![]() și spunem ca
a conduce
și spunem ca
a conduce ![]() la
la ![]() in E. in
continuare omitem pe E și notam
in E. in
continuare omitem pe E și notam ![]() . Pentru o secvența de tranziții
. Pentru o secvența de tranziții ![]() scriem
scriem ![]() cand
cand ![]() . In acest caz spunem ca
. In acest caz spunem ca ![]() este o
urma/traseu a lui E. In final,
este o
urma/traseu a lui E. In final, ![]() inseamna ca
exista o secvența
inseamna ca
exista o secvența ![]() astfel incat
astfel incat ![]() . Spunem ca
. Spunem ca ![]() este accesibil din
este accesibil din ![]() daca
daca ![]() .
.
Un invariant de tip locatie
este un vector ![]() astfel incat
astfel incat ![]() .
.
Starea mașinii poate reprezenta conflicte intre o
locație/poziție și cateva tranziții de ieșire, dar ele
nu pot reprezenta concurența și sincronizarea. Formal, fie ![]() o rețea Petri, N este o stare a mașinii
daca
o rețea Petri, N este o stare a mașinii
daca ![]() . Starea mașinii se modeleaza dificil cu
rețele Petri.
. Starea mașinii se modeleaza dificil cu
rețele Petri.
Rețele Petri fluxuri de lucru(rețele WF) sunt rețele in care nodul inițial și cel final indica respectiv starea inițiala și finala a procesului in cauza [17],[19].
Definiția 1. O rețea Petri este o rețea fluxuri de lucru (rețea WF) daca:
N are
doua locații speciale: i și f locația
inițiala i este locație susrsa ![]() Ø, și locația finala este locatia de
iesire
Ø, și locația finala este locatia de
iesire ![]() Ø.
Ø.
pentru orice nod ![]() exista o cale de
la i la n și de la n la f.
exista o cale de
la i la n și de la n la f.
Presupunem ca locația inițiala a rețelei fluxuri de producție poate conține un numar arbitrar de jetoane, cu scopul de a furniza criterii corecte pentru proiectarea acestor rețele. Corectitudinea consta in terminarea normala, care este denumita stabilitate in teoria rețelelor WF [17],[19],[43].
Definiția 2. N este k-stabila
pentru unii ![]() , daca pentru toți
, daca pentru toți ![]() ; N este stabila daca ea este k-stabila
pentru toți
; N este stabila daca ea este k-stabila
pentru toți ![]() .
.
1. Rețele RCWF
Rețelele WF specifica prelucrarea sarcinilor in interiorul organizației (societații comerciale), fara a lua in considerare resursele disponibile pentru efectuare/execuție. Extindem noțiunea de rețea WF prin includerea informației despre folosirea resursei intr-un model. In general, fiecare resursa aparține unui anume tip, avem o locație pentru un tip de resursa in rețea unde resursele sunt localizate cand ele sunt inactive. Repetam inca odata presupunerea ca resursele sunt durabile și nu pot fi create sau distruse[18].
Definiția 3: O rețea WF ![]() cu locațiile
inițiale și finale
cu locațiile
inițiale și finale ![]() este o rețea RCWF
cu mulțimea
este o rețea RCWF
cu mulțimea ![]() a locațiilor de
producție și mulțimea
a locațiilor de
producție și mulțimea ![]() a locațiilor resursa daca:
a locațiilor resursa daca:
![]() Ø;
Ø;
![]() sunt aplicații
sunt aplicații ![]() N;
N;
![]() sunt aplicații
sunt aplicații ![]() N;
N;
![]() este o rețea WF,
care o denumim rețea de producție a rețelei N.
este o rețea WF,
care o denumim rețea de producție a rețelei N.
Extindem semantica rețelelor Petri prin introducerea noțiunii de Id-jeton, identificator al jetonului, similar cu o culoare (un atribut) atașata acestuia. Rețeaua RCWF va avea doua tipuri de jetoane:
jetoane colorate pe locațiile
de producție, care sunt o pereche (p,a), unde p este o
locație și ![]() un identificator;
un identificator;
jetoane necolorate in locațiile resursa.
Presupunem ca Id este o mulțime numarabila.
Putem scrie ![]() pentru proiecția
lui
pentru proiecția
lui ![]()
![]() pe locațiile de
producție (marcaje colorate), și
pe locațiile de
producție (marcaje colorate), și ![]() proiecția lui x
pe locațiile resursa (parți necolorate). O tranziție
proiecția lui x
pe locațiile resursa (parți necolorate). O tranziție ![]() este valida in m daca
este valida in m daca ![]() și exista
și exista ![]() astfel incat
astfel incat ![]() conține jetoane
pe
conține jetoane
pe ![]() cu identificatorul a.
O actiune a lui t rezulta in cosumarea acestor jetoane și
producerea jetoanelor cu identificator a la
cu identificatorul a.
O actiune a lui t rezulta in cosumarea acestor jetoane și
producerea jetoanelor cu identificator a la ![]() și jetoane
necolorate pe
și jetoane
necolorate pe ![]() .
.
Rețelele WF cu Id-jetoane (care sunt o varianta a retelelor Petri colorate), permit prin expresivitatea lor proiectarea proceselor modelate și separarea diferitelor cazuri.
Stabilitatea rețelelor WF reprezinta proprietatea ca fiecare marcaj accesibil din marcajul inițial cu k jetoane pe locația inițiala termina normal, pot ajunge marcaje cu k jetoane pe locația finala, pentru orice numar arbitrar k. In rețele RCWF, marcajul inițial al rețelei este dat de numarul de jetoane in locația inițiala și un numar al jetoanelor resurse pe locațiile resursa. Prin terminare normala pentru rețele RCWF se ințelege ca jetoanele resurse sunt revenite pe locațiile lor cu resurse și toate sarcinile sunt corect expuse, cu excepția celor f care sunt vide/goale. Mai mult, se doreste ca sistemul verificat sa lucreze corect si in cazul in care sunt disponibile mai multe resurse.
O cerința impusa din definiția stabilitații este aceea ca jetoanele resursa nu pot fi create in timpul procesarii și la fiecare moment de timp numarul resurselor disponibile nu trebuie sa depașeasca numarul dat inițial de resurse.
Definiția 4: Fie N o rețea RCWF. N
este (k,R) -stabila pentru ![]() N,
N, ![]() daca pentru
toți
daca pentru
toți ![]() cu
cu ![]() menține:
menține: ![]() și
și ![]() .
.
N este k-stabila daca
exista ![]() , astfel incat N este
, astfel incat N este ![]() -stabila pentru toți
-stabila pentru toți ![]() .
.
N este stabila daca exista ![]() , astfel incat N este
, astfel incat N este![]() -stabila pentru toți
-stabila pentru toți ![]() N ,
N ,![]()
![]() .
.
Problema stabilitații este o problema parametrizata formulata intr-o rețea Petri colorata.
2. Rețele SM1WF
Definitia 5. Fie N
o rețea SM1WF.. Resursa efect ![]() , producția P și consumul C sunt definite dupa cum urmeaza:
, producția P și consumul C sunt definite dupa cum urmeaza:
pentru
o cale vida ![]()
pentru
o tranziție t, ![]()
![]() și
și ![]()
pentru
o cale (secvența de tranziții, urmata de o tranziție) ![]()
![]() și pentru o cale
și pentru o cale ![]()
Noțiunea de efect ne
permite sa distingem trei diferite forme ale noțiunii de cale pentru ![]() :
:
C-cale (consumption path) daca ![]()
E-cale (equality path) daca ![]()
P-cale (production path) daca ![]()
Lema
urmatoare afirma faptul ca pentru executarea secvenței ![]() sunt necesare cel puțin
sunt necesare cel puțin ![]() resurse și dupa
execuția secvenței
resurse și dupa
execuția secvenței ![]() raman
disponibile cel puțin
raman
disponibile cel puțin ![]() resurse. Acesta este un rezultat foarte important care
ne permite sa ilustram evoluția resurselor in dinamica sistemului.
resurse. Acesta este un rezultat foarte important care
ne permite sa ilustram evoluția resurselor in dinamica sistemului.
Lemma 1. Fie ![]() o cale in N.
Atunci:
o cale in N.
Atunci:
1. Daca ![]() pentru unele marcaje M, M', atunci M'(r) ≥
pentru unele marcaje M, M', atunci M'(r) ≥ ![]() și M(r) ≥
și M(r) ≥ ![]()
![]()
Corolar 1. ![]() și
și ![]() pentru toți
pentru toți ![]()
Corolar 2. Fie k > 0 și ![]() o cale astfel incat
o cale astfel incat ![]() .
Atunci,
.
Atunci,
![]()
In continuare aratam ca in condiții sigure doua cai pot fi comutate.
Lema 2. (Interchange Lemma). Fie M, M' marcaje ![]() drumuri astfel incat
drumuri astfel incat ![]() , și
, și ![]() nu este succesorul lui
nu este succesorul lui ![]() . Daca
. Daca
![]() atunci
atunci ![]()
Dem. Fie M1 un marcaj astfel incat ![]() Din
Din ![]()
![]() Atunci,
Atunci, ![]() . Daca
. Daca![]() , atunci
exista un marcaj M2
astfel incat
, atunci
exista un marcaj M2
astfel incat ![]() și
și ![]() Așadar,
Așadar, ![]() . Dar
. Dar ![]() , deci
, deci ![]() și astfel
și astfel ![]()
Urmatoarea Lema ne furnizeaza limita inferioara a numarului de resurse in stari atinse din marcajul inițial și stari ce pot fi atinse de marcajul final. Acest rezultat este folosit in demonstrația unor teoreme ulterioare.
Lemma 3. Fie![]() NP cu M(r) < M'(r).
NP cu M(r) < M'(r).
Daca ![]() , atunci
exista o C-cale
, atunci
exista o C-cale ![]() astfel incat
astfel incat ![]()
Daca ![]() , atunci
exita o P-cale
, atunci
exita o P-cale ![]() astfel incat
astfel incat ![]()
Lemma 4. Fie k0
> 0 și fie ![]() o C-cale. Atunci exista k > k0
și R
o C-cale. Atunci exista k > k0
și R![]() N astfel incat
N astfel incat ![]()
Dem. Fie p=![]() , q=
, q=![]() Atunci exista un
Atunci exista un ![]() cu
cu ![]() Din presupunerea existenței locației invariante ,
Din presupunerea existenței locației invariante , ![]()
Din corolar 2, ![]() k[i]
+ pentru toti k > 0. din
k[i]
+ pentru toti k > 0. din ![]() < 0, exista k > k0 astfel incat
< 0, exista k > k0 astfel incat ![]() Luand
Luand ![]() , și
din Corolarul 2.:
, și
din Corolarul 2.: ![]()
Construcția descrisa in demonstrația lemei anterioare poate fi folosita pentru a da sensul verificarii feedback-ul in rețele ce nu sunt stabile.
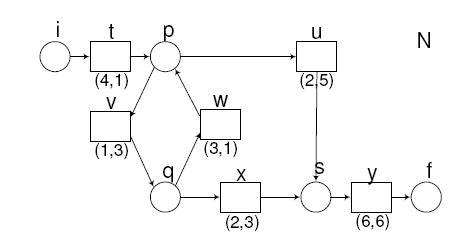
Fig. 1. Rețea stabila
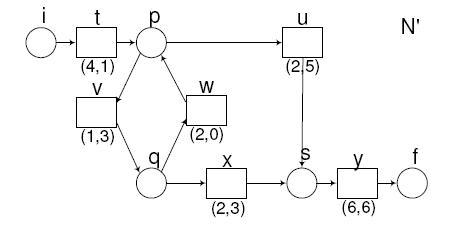
Fig. 2. Exemplu de rețea RCWF care nu este stabila
Exemplu 1. Consideram C-calea ![]() in rețeaua N' din
Fig. 2.
in rețeaua N' din
Fig. 2. ![]() . Luam tv
ca
. Luam tv
ca ![]()
![]() . Alegem un k
. Alegem un k
![]() N
ce satisface
N
ce satisface ![]() adica
k
adica
k ![]() 1.5, și alegem R ca
1.5, și alegem R ca ![]() .
Atunci
.
Atunci ![]() Remarcam
ca nu exista resurse ramase și de aceea obținem un
blocaj care necesita resurse pentru a continua.
Remarcam
ca nu exista resurse ramase și de aceea obținem un
blocaj care necesita resurse pentru a continua.
Teorema urmatoare ne da o condiție necesara și suficienta pentru stabilitatea rețelelor SM1WF(State Machine 1-soundness Workflow)[17],[19].
Teorema 1. O rețea SM1WF, N este stabila
daca exista un invariant unic de tip locație W astfel
incat W(i) = W(f) = 0, W(r) = 1, și mai mult W(p) ![]() 0 pentru toți p
0 pentru toți p ![]() Pp, și pentru fiecare C-cale
Pp, și pentru fiecare C-cale ![]() atunci exista un
succesor P-cale
atunci exista un
succesor P-cale ![]() astfel incat
astfel incat ![]()
![]() Dem.
Dem. ![]() ): Presupunem ca exista o C-cale
): Presupunem ca exista o C-cale ![]() astfel incat toți succesorii lui P-cale
astfel incat toți succesorii lui P-cale ![]() satisfac
satisfac![]() Din Lema 4,
atunci exista k și R >
Din Lema 4,
atunci exista k și R > ![]() astfel incat
astfel incat
![]() . Daca
. Daca ![]() , și Lema 3. exista P-cale
, și Lema 3. exista P-cale ![]() cu
cu ![]() ceea ce
contrazice presupunerea. Deci,
ceea ce
contrazice presupunerea. Deci, ![]() și
rețeaua nu este stabila.
și
rețeaua nu este stabila.
![]() ): Fie R0
un maxim C
): Fie R0
un maxim C ![]() peste
toate drumurile
peste
toate drumurile ![]() din N
cu
din N
cu ![]() = f. Alegerea lui R asigura ca daca cel
puțin o resursa R este prezenta,
un jeton in rețeaua producției poate fi transferat cu succes din
locație pana la cea finala f.
= f. Alegerea lui R asigura ca daca cel
puțin o resursa R este prezenta,
un jeton in rețeaua producției poate fi transferat cu succes din
locație pana la cea finala f.
Presupunem ![]() și
și ![]() . Prin inducție demonstram R - M(r) ca
atunci exista un marcaj M' cu M'(r) = R astfel incat
. Prin inducție demonstram R - M(r) ca
atunci exista un marcaj M' cu M'(r) = R astfel incat ![]() , pentru orice marcaj accesibil exista o cale de
de a continua și de a permite returnarea tuturor resurselor consumate(pe
aceasta cale). Notam
, pentru orice marcaj accesibil exista o cale de
de a continua și de a permite returnarea tuturor resurselor consumate(pe
aceasta cale). Notam ![]() intrucat numarul
resurselor consumate este totdeauna nenegativ, astfel incat resursele nu pot fi
create. (datorita existenței invariantului de tip locațieW). Daca
M(r) = R, expunerea este evidenta. Daca M(r) < R, și
aplicam Lema 3 pentru
intrucat numarul
resurselor consumate este totdeauna nenegativ, astfel incat resursele nu pot fi
create. (datorita existenței invariantului de tip locațieW). Daca
M(r) = R, expunerea este evidenta. Daca M(r) < R, și
aplicam Lema 3 pentru ![]() , atunci exista a C-cale
, atunci exista a C-cale ![]() astfel incat
astfel incat ![]() . Din condiția teoremei, avem P-cale
. Din condiția teoremei, avem P-cale ![]() și un
marcaj
și un
marcaj ![]() astfel incat
astfel incat ![]() , so
, so ![]() . Intrucat M"(r) > M(r), ipoteza
inducției este aplicabila pentru M", in final obținem
. Intrucat M"(r) > M(r), ipoteza
inducției este aplicabila pentru M", in final obținem ![]() și M'(r)
= R.
și M'(r)
= R.
Fie p ![]() Pp astfel incat M'(p) > 0. Atunci din R
Pp astfel incat M'(p) > 0. Atunci din R
![]() R și din alegerea lui R0, avem
R și din alegerea lui R0, avem ![]() . Deci
. Deci ![]() .Aceasta procedura se repeta pentru toți
.Aceasta procedura se repeta pentru toți ![]() cu M(p)
> 0, atingand/obținand
cu M(p)
> 0, atingand/obținand ![]()
Rețeaua nu este stabila daca ea conține un blocaj/deadlock (un marcaj intermediar ce nu are suficiente resurse pentru o etapa urmatoare) sau o ciclarel/livelock (exista suficiente resurse pentru o etape/pași urmatoare, dar aceste etape nu duc la o terminare proprie).
3. Algoritmul de decizie
Condiția formulata in teorema 1 ne permite sa caracterizam stabilitatea rețelelor -SM1WF. Condiția data nu poate fi verificata direct, intrucat trebuie luate in considerare o multitudine de cai. Remarcam ca este suficienta verificarea unui numar finit de cai.
Algoritmul de decizie prezentat in continuare are gradul de complexitate polinomial in contextul rețelei SM1WF.
Lema 6. Fie ![]() un drum ciclic (adica
un drum ciclic (adica ![]() Atunci pentru orice
Atunci pentru orice ![]()
![]() astfel incat
astfel incat ![]() și
și ![]() avem
avem ![]()
![]() , și
, și ![]()
Deci, pentru verificarea condiției teoremei 1. este suficient sa consideram numai cai ciclice. Daca caile aciclice sunt finite, stabilitatea rețelei SM1WF este decidabila. Stabilitatea rețelei RCWF poate fi redusa la stabilitatea rețelei SM1WF, adica:
Corolar 3. Stabilitatea rețelei RCWF cu o resursa este decidabila.
In continuare vor fi enunțate leme și corolare care servesc la algoritmul de decizie.
Lema 7. Fie ![]() cai astfel incat
cai astfel incat ![]() .
Atunci,
.
Atunci, ![]() și
și ![]()
Corolar 4. N este stabila daca și numai daca
![]()
Analog Corolarului 2, putem arata ca rețeaua SM1WF-nu are deadlock/impas daca
![]()
Cu aceste condiții putem determina daca rețeaua SM1WF este stabila, instabilitatea implica blocaj/deadlock sau ciclare/livelock
Funcția ![]() indeplinește
urmatoare proprietate:
indeplinește
urmatoare proprietate:
Lema 8. Pentru toți p și q in Pp
avem ![]()
Lema 8 conduce la
urmatorul algoritm pentru calcularea lui ![]() Pentru doua matrici
Pentru doua matrici ![]() definim
definim![]() unde
unde ![]() . Matricea
. Matricea ![]() este calculata inițializand matricea
este calculata inițializand matricea
![]() cu
cu ![]() și
și ![]() Calculand puterile matricii A putem
obține punctele fixe și pe baza lor caile de lungime maxima
k. Procesul se considera terminat cand nu mai exista nici o cale
aciclica.
Calculand puterile matricii A putem
obține punctele fixe și pe baza lor caile de lungime maxima
k. Procesul se considera terminat cand nu mai exista nici o cale
aciclica.
Exemplu 2. In exemplul din Fig. 1, o tranziție t din i la p și W(i) = 0, W(p) = 3, C(t) = 4, P(t) = 1, cu condiția inițiala a(i, p) = 4 . Matricea inițiala a iterațiilor devine:
|
A |
i |
p |
q |
S |
f |
||
|
i |
|
|
|
|
|||
|
p |
|
|
|||||
|
q |
|
|
|||||
|
s |
|
|
| ||||
|
f |
|
|
|
|
|
A2 |
i |
p |
q |
s |
f |
||
|
i |
|
||||||
|
p |
| ||||||
|
q |
| ||||||
|
s |
|
|
| ||||
|
f |
|
|
|
|
|
A3 |
i |
p |
q |
s |
f |
||
|
i | |||||||
|
p |
| ||||||
|
q |
| ||||||
|
s |
|
|
| ||||
|
f |
|
|
|
|
Dar A4 = A3,
deci A3 ne da ![]() . Verificam condiția:
. Verificam condiția: ![]()
![]() pentru
pentru ![]() , de aici W(i)
= W(r) = W(f) = 0 și nici o
locație nu are o pondere mai mica. Din W(p) = 3 și toate
celelalte locații au pondere mai mica, avem
, de aici W(i)
= W(r) = W(f) = 0 și nici o
locație nu are o pondere mai mica. Din W(p) = 3 și toate
celelalte locații au pondere mai mica, avem ![]() și
și ![]() . In final, pentru x = q avem
. In final, pentru x = q avem ![]() și
și ![]() . Condiția este indeplinita,deci rețeaua este
stabila.
. Condiția este indeplinita,deci rețeaua este
stabila.
Consideram rețeaua N' din Fig. 2. Atunci ![]() este calculat dupa cum urmeaza:
este calculat dupa cum urmeaza:
|
A |
i |
p |
q |
S |
f |
||
|
i |
|
|
|
||||
|
p |
|
|
|||||
|
q |
|
|
|||||
|
s |
|
|
| ||||
|
f |
|
|
|
|
|
A2 |
i |
p |
q |
s |
f |
||
|
i |
|
||||||
|
p |
| ||||||
|
q |
| ||||||
|
s |
|
|
| ||||
|
f |
|
|
|
|
|
A3 |
i |
p |
q |
s |
f |
||
|
i | |||||||
|
p |
| ||||||
|
q |
| ||||||
|
s |
|
|
| ||||
|
f |
|
|
|
|
A3 este punct fix . Acum, ![]() și
și ![]() , deci
rețeaua nu este stabila. Mai mult,
, deci
rețeaua nu este stabila. Mai mult, ![]() , și
se poate folosi construcția din demonstrația lemei 4. pentru a gasi blocajul acestei
rețele.
, și
se poate folosi construcția din demonstrația lemei 4. pentru a gasi blocajul acestei
rețele.
|
Politica de confidentialitate |
| Copyright ©
2024 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |