
Reglarea directa a cuplului motorului asincron alimentat de la un invertor sursa de tensiune (VSI)
1. Bazele fizice si matematice ale producerii raspunsului rapid al cuplului
In cazul reglarii directe a cuplului (Direct Torque Control - DTC) unui motor asincron alimentat de la un invertor, abaterile (erorile) dintre valorile impuse (de referinta) si valorile reale (estimate) ale fluxului si cuplului fac posibila reglarea directa a starilor invertorului pentru a aduce abaterile in interiorul benzilor de histerezis fixate ale fluxului respectiv cuplului. In acest fel schema de reglare nu necesita regulator de curent, transformari de coordonate si generator de semnale PWM, se obtine un raspuns rapid al cuplului, o frecventa de comutatie a invertorului joasa si pierderi armonice reduse [21], [22], [23].
In cele ce urmeaza se va descrie o reglare directa a cuplului in care, pe langa controlul cuplului electromagnetic, fluxul controlat este fluxul statoric.Trebuie observat ca se poate realiza si o alta implementare in care fluxul rotoric sau fluxul de magnetizare sa fie controlat. Controlul direct al cuplului permite raspunsuri foarte rapide ale cuplului si o reglare flexibila a masinii asincrone.
Intr-o masina asincrona trifazata cuplul electromagnetic instantaneu este proportional cu produsul vectorial al fazorului statial al fluxului statoric si al curentului statoric (ecuatia 2.107):
![]() (5.1)
(5.1)
In relatia (5.1) ambii fazori sunt exprimati in sistemul bifazat statoric (fix) d - q (fig. 5.1).
Considerand fazorii:
![]() si
si ![]()
 ecuatia (5.1) devine:
ecuatia (5.1) devine:
![]() (5.2)
(5.2)
unde
![]() este unghiul dintre
fazorul spatial al fluxului statoric si cel al curentului statoric.
este unghiul dintre
fazorul spatial al fluxului statoric si cel al curentului statoric.
Se poate arata ca, prin utilizarea ecuatiilor de tensiune ale masinii asincrone, pentru o valoare data a vitezei rotorului - daca modulul fazorului spatial al fluxului statoric este mentinut constant - si unghiul s se modifica rapid, atunci cuplul electromagnetic se poate modifica rapid.
Pentru dovada matematica se obtine acum raspunsul cuplului electromagnetic al masinii la o schimbare in treapta a s la t = 0. De aceea trebuie determinata variatia in timp a cuplului electromagnetic [21].
In acest scop se exprima mai intai fazorul spatial al curentului rotoric (raportat la sistemul statoric fix, d - q) in functie de fazorul spatial al fluxului statoric. In sistem statoric ( 0) ecuatia fazoriala a fluxului statoric (ecuatia 2.52) era:
![]()
Notam
![]() si vom avea:
si vom avea:
![]() .
.
De aici rezulta:
![]() . (5.3)
. (5.3)
Exprimam apoi fazorul spatial al fluxului rotoric (din ecuatia 2.53) in sistem statoric, fix d - q.

Inlocuim in aceasta relatie pe i'r din relatia (5.3) si notand:

obtinem:
![]() (5.4)
(5.4)
Relatiile (5.3) si (5.4) le substituim in ecuatia tensiunii rotorice in sistem statoric. Pentru rotorul in scurtcircuit si ecuatia (2.18) devine:
![]()
In
acest fel ecuatia tensiunii rotorice obtinute contine is
si s si aceasta poate fi folosita
pentru a exprima fazorul spatial al curentului statoric in functie de
fazorul spatial al fluxului statoric. Aceasta expresie se substituie
in ecuatia (5.1). De asemenea prin utilizarea in acesta expresie a
faptului ca modulul fazorului spatial al fluxului este constant (s
= k1) deci ![]() si prin urmare
si prin urmare ![]() , in final este posibil sa obtinem o ecuatie
pentru cuplul electromagnetic a carei transformata inversa
, in final este posibil sa obtinem o ecuatie
pentru cuplul electromagnetic a carei transformata inversa
Cu alte cuvinte, daca se impun tensiunile statorice ale motorului, care mentin fluxul statoric constant (la valoarea necesara), dar care rotesc fazorul fluxului statoric in pozitia necesara (la cuplu cerut), se executa controlul rapid al cuplului. Urmeaza ca daca, in controlul direct al cuplului motorului asincron, cuplul electromagnetic real este mai mic decat valoarea impusa, cuplul electromagnetic ar trebui crescut, cat mai rapid posibil, prin folosirea celui mai rapid ds/dt. Totusi, cand cuplul electromagnetic este egal cu valoarea impusa (de referinta) rotatia se opreste. Daca fazorul fluxului statoric accelereaza in sens direct (inainte) atunci se produce cuplu electrmegnetic pozitiv si cand se decelereaza in sens invers (inapoi) se produce cuplu electromagnetic negativ. In orice caz, fazorul fluxului statoric se poate ajusta prin utilizarea celui mai potrivit fazor al tensiunii statorice, care este generat de invertorul sursa de tensiune ce alimenteaza masina asincrona (a se vedea mai jos detaliile generarii tensiunii). Pentru a rezuma: cuplul electromagnetic se poate schimba rapid prin comanda fazorului spatial al fluxului statoric, care se poate modifica prin utilizarea tensiunilor statorice potrivite (generate de invertorul care alimenteaza motorul sincron). Se poate observa ca exista controlul direct al fluxului statoric si cuplului electromagnetic utilizand tensiunile statorice potrivite. Acesta este motivul pentru care acest tip de control este uzual denumit controlul direct al cuplului.
Este foarte util sa consideram o alta forma de exprimare pentru cuplul electromagnetic instantaneu, care da o imagine fizica extrem de clara a proceselor produse dar conduce la aceleasi rezultate, cum s-a aratat mai inainte. Considerand ca:
![]()
si:
![]()
unde din nou marimile rotorice notate cu prim sunt exprimate in sistemul statoric, fix, d - q, din relatia (5.4) rezulta:

 (5.5)
(5.5)
Inlocuind (5.5) in (5.1) se obtine:
![]()
![]() (5.6)
(5.6)
In
ecuatia (5.6) este unghiul dintre fazorii spatiali ai
fluxului statoric si rotoric, ![]() , unde r este unghiul
fazorului spatial al fluxului rotoric fata de axa reala a
sistemului statoric, fix, cum se arata in figura
, unde r este unghiul
fazorului spatial al fluxului rotoric fata de axa reala a
sistemului statoric, fix, cum se arata in figura
El poate fi presupus constant. Aceasta rezulta de asemenea din ecuatia tensiunii rotorice a masinii asincrone daca se presupune fluxul statoric constant. Daca fluxurile statoric si rotoric sunt presupuse constante, din ecuatia (5.6) urmeaza ca cuplul electromagnetic poate fi rapid schimbat prin schimbarea lui in sensul cerut (care este determinat de comanda cuplului). Aceasta este in esenta controlul direct al cuplului. Asa cum se va discuta in continuare unghiul poate fi usor schimbat prin comutatia fazorului spatial potrivit al tensiunii statorice (produs de tensiunea potrivita a invertorului). Daca modulul fazorului spatial al fluxului statoric nu este constant (de exemplu in domeniul slabirii campului), atunci este totusi posibil sa controlam ambele marimi (unghiul si modulul s) prin comutatia potrivita a tensiunii invertorului.
In contrast cu reglarea vectoriala (cu orientare in camp) a motorului asincron unde curentii statorici se utilizeaza ca marimi comandate, in controlul direct al cuplului, fluxul statoric este comandat. Trebuie observat ca daca r este constant, din ecuatia (4.9) rezulta ca:
![]()
unde
isy este curentul statoric care produce cuplul in sistemul de axe
orientat dupa fluxul rotoric (dr - qr) notate in figura
5.2 cu x si y si cuplul electromagnetic poate fi rapid schimbat prin
scimbarea rapida a lui isy. In reglarea cu orientare dupa
camp curentii statorici sunt marimi comandate (isy
comanda cuplul si isx comanda fluxul rotoric). Acesta
este motivul pentru care, intr-o actionare comandata vectorial cu
orientare dupa fluxul rotoric, curentii statorici exprimati in
sistem statoric fix (d - q) trebuie transformati in curenti statorici
in sistem orientat dupa fluxul rotoric (dr - qr). Din
figura (5.2) sau relatia (5.6) rezulta ca ![]() este componenta
fluxului statoric care produce cuplul si componenta sx este colineara
cu fluxul rotoric. In figura (5.2) fluxul statoric s
a rezultat din relatia (5.4).
este componenta
fluxului statoric care produce cuplul si componenta sx este colineara
cu fluxul rotoric. In figura (5.2) fluxul statoric s
a rezultat din relatia (5.4).
Astfel fluxul este comandat de componenta directa a fluxului statoric (in sistem orientat dupa fluxul rotoric) si cuplul de componenta in cuadratura a fluxului statoric si din nou poate fi observat ca in comparatie cu controlul vectorial acum componentele sunt marimi de comanda. Ecuatia (5.6) este similara cu cea a unei masini sincrone unde cuplul electromagnetic este comandat de unghiul de sarcina dintre fluxul statoric si rotoric. Intr-un regim tranzitoriu scurt, fluxul rotoric este aproape neschimbat astfel ca schimbarile rapide ale cuplului electromagnetic pot fi produse prin rotatia fluxului statoric in sensul inainte (avans de faza) sau prin rotatia in sens negativ (intarziere) sau prin oprirea lui, conform cu cuplul cerut. in rezumat: in reglarea directa a cuplului, reglarea rapida a cuplului instantaneu poate fi realizata prin schimbarea rapida a pozitiei fazorului spatial al fluxului statoric (fata de fazorul spatial al fluxului rotoric) sau, cu alte cuvinte prin schimbarea rapida a vitezei sale (viteza fazorului spatial al fluxului statoric). In orice caz, fazorul spatial al fluxului statoric (modulul si argumentul sau) poate fi schimbat prin tensiunile statorice [21].
Pentru simplificare,
presupunand ca neglijam caderea de tensiune pe rezistenta
statorica, ![]() , se
observa ca tensiunea invertorului (us = ui)
determina direct fluxul statoric si astfel locul geometric al
fluxului statoric necesar se va obtine prin utilizarea tensiunilor
potrivite ale invertorului (prin folosirea starilor de comutatie
potrivite ale invertorului). Pentru o mai buna intelegere se va
discuta aceasta in detaliu. Din
, se
observa ca tensiunea invertorului (us = ui)
determina direct fluxul statoric si astfel locul geometric al
fluxului statoric necesar se va obtine prin utilizarea tensiunilor
potrivite ale invertorului (prin folosirea starilor de comutatie
potrivite ale invertorului). Pentru o mai buna intelegere se va
discuta aceasta in detaliu. Din ![]() rezulta
ca, intr-un interval scurt de timp t, cand se aplica vectorul
de tensiune,
rezulta
ca, intr-un interval scurt de timp t, cand se aplica vectorul
de tensiune, ![]() . Astfel spus fazorul fluxului statoric se misca cu
s in directia vectorului spatial al
tensiunii statorice la o viteza care este proportionala cu
marimea vectorului spatial al tensiunii statorice (care este
proportionala cu tensiunea din circuitul intermediar de c.c.). Prin
selectarea pas cu pas a vectorului potrivit al tensiunii statorice, este deci
posibil sa schimbam fluxul statoric in modul necesar. Comanda
decuplata a cuplului si fluxului statoric se realizeaza prin
actiunea componentelor radiale si tangentiale ale fazorului
fluxului statoric in locul geometric. Aceste doua componente sunt direct
proportionale (daca se neglijeaza caderea de tensiune
ohmica) cu componentele fazorului tensiunii statorice in aceleasi
directii si astfel ele pot fi comandate prin comutatiile
potrivite ale invertorului. Ar trebui subliniat ca pentru producerea
cuplului, unghiul joaca un rol esential sau altfel spus,
pozitia relativa a fazorilor spatiali ai fluxului statoric
si rotoric determina cuplul electromagnetic. Presupunand o
miscare lenta a fazorului fluxului rotoric, daca se aplica
un vector al tensiunii statorice, care produce o miscare rapida a
fazorului spatial al fluxului statoric fata de fluxul rotoric,
atunci cuplul electromagnetic va creste, deoarece unghiul va
creste. Daca se aplica un vector spatial de tensiune
statorica zero (a se vedea mai jos), care aproape opreste
rotatia fazorului spatial al fluxului statoric, atunci cuplul
electromagnetic va scadea, deoarece fazorul spatial al fluxului
rotoric inca se mai misca si unghiul va
scadea. Daca durata vectorului zero a tensiunii este suficient de
mare, atunci - deoarece fazorul fluxului statoric aproape nu se va misca
(in practica el se va misca datorita caderii ohmice de
tensiune) - fazorul spatial al fluxului rotoric va depasi
fazorul spatial al fluxului statoric, unghiul isi va schimba
semnul si cuplul electromagnetic isi va schimba directia [8],
[9], [21].
. Astfel spus fazorul fluxului statoric se misca cu
s in directia vectorului spatial al
tensiunii statorice la o viteza care este proportionala cu
marimea vectorului spatial al tensiunii statorice (care este
proportionala cu tensiunea din circuitul intermediar de c.c.). Prin
selectarea pas cu pas a vectorului potrivit al tensiunii statorice, este deci
posibil sa schimbam fluxul statoric in modul necesar. Comanda
decuplata a cuplului si fluxului statoric se realizeaza prin
actiunea componentelor radiale si tangentiale ale fazorului
fluxului statoric in locul geometric. Aceste doua componente sunt direct
proportionale (daca se neglijeaza caderea de tensiune
ohmica) cu componentele fazorului tensiunii statorice in aceleasi
directii si astfel ele pot fi comandate prin comutatiile
potrivite ale invertorului. Ar trebui subliniat ca pentru producerea
cuplului, unghiul joaca un rol esential sau altfel spus,
pozitia relativa a fazorilor spatiali ai fluxului statoric
si rotoric determina cuplul electromagnetic. Presupunand o
miscare lenta a fazorului fluxului rotoric, daca se aplica
un vector al tensiunii statorice, care produce o miscare rapida a
fazorului spatial al fluxului statoric fata de fluxul rotoric,
atunci cuplul electromagnetic va creste, deoarece unghiul va
creste. Daca se aplica un vector spatial de tensiune
statorica zero (a se vedea mai jos), care aproape opreste
rotatia fazorului spatial al fluxului statoric, atunci cuplul
electromagnetic va scadea, deoarece fazorul spatial al fluxului
rotoric inca se mai misca si unghiul va
scadea. Daca durata vectorului zero a tensiunii este suficient de
mare, atunci - deoarece fazorul fluxului statoric aproape nu se va misca
(in practica el se va misca datorita caderii ohmice de
tensiune) - fazorul spatial al fluxului rotoric va depasi
fazorul spatial al fluxului statoric, unghiul isi va schimba
semnul si cuplul electromagnetic isi va schimba directia [8],
[9], [21].
Considerand un invertor sursa de tensiune (VSI fig. 5.3.a) exista sase fazori spatiali diferiti de zero (u1, u2, , u6) si doi fazori zero (u7 si u8) (fig. 5.3.b). Cei sase fazori activi de comutatie a invertorului se pot exprima ca:
 (5.7)
(5.7)
unde E este tensiunea din circuitul intermediar de curent continuu. Cele sase sectoare, de 600, se delimiteaza avand bisectoare a unghiurilor vectorii de comutatie (fig. 5.3.b). Deoarece:
![]()
fazorul u1 se aliniaza cu axa reala d a sistemului bifazat fix, statoric.
Deoarece s
= us t,
se poate observa ca fazorul spatial al fluxului statoric se va
misca rapid, daca se aplica vectorii de comutatie activi
(diferiti de zero), iar pentru un vector de comutatie zero el aproape
se va opri (se va misca foarte incet datorita caderii ohmice de
tensiune mici). Pentru un invertor cu sase pulsuri fluxul statoric se
misca de-a lungul unei traiectorii hexagonale cu o viteza
liniara

In actionarea cu reglare
directa a cuplului (DTC), la fiecare perioada de esantionare,
vectorii de comutatie se selecteaza pe baza mentinerii erorilor
fluxului statoric intr-o banda de toleranta necesara (banda
de histerezis) si mentinerea erorii cuplului, in banda sa de histerezis.
Se presupune ca latimile acestor benzi de histerezis sunt 2.s
si respectiv 2.me (factorul 2 apare in aceasta
definitie deoarece se presupune ca - de exemplu pentru fluxul static
- valoarea limita superioara este peste valoarea impusa cu s
si valoarea limita inferioara este sub s,
astfel ca latimea benzii de histerezis este intra-adevar 2.s).
Daca fazorul spatial al fluxului se afla in sectorul k, unde k =
1, 2, , 6, valoarea sa poate fi crescuta prin folosirea vectorilor de
comutatie uk, uk+1 si uk-1;
marimea sa poate fi scazuta prin selectarea vectorilor uk+2,
uk-2 si uk+3. Evident ca vectorii
de comutatie a tensiunii selectati afecteaza si cuplul
electromagnetic. Viteza fazorului spatial al fluxului statoric este zero
daca se selecteaza un vector de comutatie zero si este
posibil sa schimbam aceasta viteza prin schimbarea
raportului de iesire dintre vectorii de tensiune zero si cei
diferiti de zero. Este important de observat ca durata starilor
zero are un efect direct asupra oscilatiilor cuplului electromagnetic.

Dupa cum s-a aratat mai
inainte, fazorul spatial al fluxului statoric este integrala fazorului
spatial al tensiunii statorice si se va misca in directia
fazorului tensiunii statorice atat timp cat se aplica fazorul spatial
al tensiunii. Astfel daca se cere o reducere a modulului fazorului
spatial al fluxului statoric, modulul acestui fazor poate fi comandat prin
aplicarea vectorilor de comutatie a tensiunii care sunt indreptati
catre centru si daca se cere o crestere a modulului fazorului
spatial al fluxului statoric, el poate fi comandat prin aplicarea
vectorilor de tensiune care sunt indreptati de la centru. Aceasta este
ilustrata in fig. 5.4 unde ![]() este valoarea de
referinta (impusa) a fazorului spatial al fluxului
statoric. Scopul nostru este de a mentine modulul fazorului spatial
al fluxului statoric in interiorul benzii de histerezis (indicate prin
cercuri) a carei latime este de 2.s
(fig. 5.4). Presupunem initial ca fazorul spatial al fluxului
este in pozitia P0, deci in sectorul 1. Presupunand ca
fazorul fluxului statoric se roteste in sens direct trigonometric
urmeaza ca, deoarece la pozitia P0 a fazorului
spatial al fluxului statoric fluxul este la limita superioara
este valoarea de
referinta (impusa) a fazorului spatial al fluxului
statoric. Scopul nostru este de a mentine modulul fazorului spatial
al fluxului statoric in interiorul benzii de histerezis (indicate prin
cercuri) a carei latime este de 2.s
(fig. 5.4). Presupunem initial ca fazorul spatial al fluxului
este in pozitia P0, deci in sectorul 1. Presupunand ca
fazorul fluxului statoric se roteste in sens direct trigonometric
urmeaza ca, deoarece la pozitia P0 a fazorului
spatial al fluxului statoric fluxul este la limita superioara ![]() , el trebuie redus. Aceasta se realizeaza prin
selectarea vectorului de comutatie corespunzator, care este vectorul u3
(fig. 5.4). In acest fel fazorul spatial al fluxului statoric se va
misca rapid de la punctul P0 la punctul P1, care
este acum in sectorul 2. Exista sase sectoare de 600
(datorita invertorului cu sase pulsuri). Acum se poate observa
ca in punctul P1 fazorul spatial al fluxului statoric este
din nou la limita superioara. Pe de alta parte, trebuie observat
ca, daca fazorul spatial al fluxului statoric se misca
in sens invers trigonometric din punctul P0, atunci ar trebui
selectat vectorul u5, deoarece acesta asigura
rotatia necesara si de asemenea descresterea dorita a
fluxului.
, el trebuie redus. Aceasta se realizeaza prin
selectarea vectorului de comutatie corespunzator, care este vectorul u3
(fig. 5.4). In acest fel fazorul spatial al fluxului statoric se va
misca rapid de la punctul P0 la punctul P1, care
este acum in sectorul 2. Exista sase sectoare de 600
(datorita invertorului cu sase pulsuri). Acum se poate observa
ca in punctul P1 fazorul spatial al fluxului statoric este
din nou la limita superioara. Pe de alta parte, trebuie observat
ca, daca fazorul spatial al fluxului statoric se misca
in sens invers trigonometric din punctul P0, atunci ar trebui
selectat vectorul u5, deoarece acesta asigura
rotatia necesara si de asemenea descresterea dorita a
fluxului.
Deoarece
in punctul P1 fazorul spatial al fluxului statoric este din nou
la limita sa superioara, el trebuie redus din nou, cand se roteste in
sens trigonometric si pentru aceasta se selecteaza vectorul de
comutatie u4, care deplaseaza s
din P1 in P2 (fig. 5.4). Punctul P2 este de
asemenea in sectorul 2. Din punctul P2, cand fazorul spatial al
fluxului rotoric este la limita sa inferioara, fluxul statoric trebuie
marit prin selectarea vectorului de comutatie u3.
Trebuie observat ca daca, de exemplu, in punctul P1 este
necesara o rotatie rapida in sens invers trigonometric, atunci
se poate vedea ca cea mai rapida rotatie se poate atinge prin
aplicarea vectorului de comutatie u6. Pe de alta
parte, daca in punctul P1 trebuie oprita rotatia
fazorului spatial al fluxului statoric atunci trebuie aplicat un vector de
comutatie zero, deci poate fi aplicat oricare din vectorii u7
sau u8. Deoarece anterior atingerii punctului P1
ultima comutatie a fost realizata prin aplicarea vectorului u3
= u3 (0 1 0), pentru a minimiza numarul de
comutatii, se selecteaza u8 (0 0 0), deoarece
necesita numai comutatia comutatorului T3 (fig. 5.3. a) de
la 1 la 0 in comparatie cu u8 (1 1 1) care ar necesita
doua comutatii T4 si T2 (de la 0 la 1).
Daca fazorul spatial al fluxului statoric este in punctul P2
atunci este atinsa limita inferioara ![]() si fazorul
spatial al fluxului statoric se poate roti in sens direct trigonometric
spre punctul P3, prin cresterea sa si in acest scop
vectorul u3 da rotatia cea mai rapida.
Daca, pe de alta parte, fazorul spatial al fluxului statoric
trebuie rotit din P2 in sens opus (invers) - prin cresterea sa
- cea mai rapida cale o da vectorul de comutatie u1,
etc.
si fazorul
spatial al fluxului statoric se poate roti in sens direct trigonometric
spre punctul P3, prin cresterea sa si in acest scop
vectorul u3 da rotatia cea mai rapida.
Daca, pe de alta parte, fazorul spatial al fluxului statoric
trebuie rotit din P2 in sens opus (invers) - prin cresterea sa
- cea mai rapida cale o da vectorul de comutatie u1,
etc.
Asa cum s-a discutat mai inainte, oprirea rotatiei fazorului spatial al fluxului statoric corespunde cazului cand cuplul electromagnetic nu poate fi schimbat (valoarea impusa este egala cu valoarea reala). Totusi, cand cuplul electromagnetic trebuie schimbat (in sens trigonometric sau invers) atunci fazorul spatial al fluxului statoric trebuie rotit in sens corespunzator. De exemplu, cand fluxul statoric se roteste in sens direct si daca este necesara o crestere a cuplului electromagnetic (cand fazorul fluxului statoric este in sectorul 2 in punctul P1 unde fluxul trebuie scazut) atunci cresterea cuplului electromagnetic poate fi obtinuta prin aplicarea vectorului de comutatie u4. Pe de alta parte, daca fazorul spatial al fluxului statoric este in sectorul 2 dar este necesara o scadere a cuplului si fluxul trebuie crescut, atunci aceasta se poate obtine prin aplicarea vectorului de comutatie u1, deoarece acesta se misca vectorul spatial al fluxului statoric in sens invers (care este sensul pentru cuplu negativ) si de asemenea creste fluxul statoric.
Daca fazorul fluxului statoric este in sectorul 2 si este necesara o scadere a cuplului, dar fluxul statoric trebuie scazut, atunci trebuie aplicat vectorul de comutatie u6, etc. Figura 5.5 arata pozitia difertilor vectori ai fluxului statoric daca fazorul spatial al fluxului statoric se afla in unul din cele sase sectoare. Este de asemenea indicat care vector de comutatie trebuie selectat pentru a obtine cresterea sau scaderea necesara a fluxului statoric si cresterea sau scaderea necesara a cuplului electromagnetic (prin producerea cuplurilor pozitive sau negative).

Trebuie observat ca, in
general, daca este necesara o crestere a cuplului, atunci cuplul
este comandat prin aplicarea vectorilor de tensiune care avanseaza fazorul
spatial al fluxului in directia de rotatie si daca
este necesara o scadere se aplica vectorii care sunt de sens
invers. Daca este necesar cuplul zero, atunci se aplica vectorul zero
(u7 sau u8) si anume acela care
minimizeaza comutatia invertorului. Urmeaza ca fazorul
spatial al tensiunii statorice este comandat indirect prin modulul
fazorului flux si prin cuplu si cresterea cuplului produce un
unghi marit.
Un cuplu necesar este atins printr-o alegere a cresterii (cuplu pozitiv) sau descresterii (cuplu negativ) sau a unui cuplu zero. Similar, modulul fazorului flux statoric este limitat printr-o alegere a cresterii (fluxul creste) sau scaderii (fluxul scade).
2. Selectia vectorului de comutatie optim (actionare cu alegerea nepredictiva a vectorului de comutatie)
Rezultatele obtinute in paragraful precedent pot fi tabelate in asa-numitul tabel de comutatie (tab. 5.1). Acesta prezinta selectia optima a vectorilor de comutatie pentru toate pozitiile posibile ale fazorului spatial al fluxului statoric (sase pozitii corespunzand celor sase sectoare din fig. 5.4 unde sectorul 1 este in domeniul lui (1), sectorul 2 in domeniul lui (2), , sectorul 6 in domeniul lui (6)) si intrarile de reglare dorite - care sunt valorile impuse (de referinta) ale modulului fluxului statoric respectiv ale cuplului electromagnetic. Daca este necesara o crestere a fluxului, atunci = 1; daca este necesara o scadere a fluxului, atunci = 0. Notatia corespunde faptului ca semnalele de iesire ale unui comparator de flux cu histerezis cu doua nivele sunt d, unde:
![]() daca
daca ![]()
![]() daca
daca ![]()
Daca este necesara o crestere a cuplului, atunci me = 1, daca este necesara o scadere, atunci me = - 1 si daca nu este necesara o modificare a cuplului, atunci me = 0. Notatia corespunde faptului ca iesirile digitale ale unui comparator cu histerezis cu trei nivele este me unde, pentru sensul de rotatie direct trigonometric (rotatie inainte):
![]() daca
daca ![]()
![]() daca
daca ![]()
si pentru sens invers (sens inapoi):
![]() daca
daca ![]()
![]() daca
daca ![]()
Tabelul 5.1. Tabelul de comutatie.
|
d |
dme |
sector 1 |
sector 2 |
sector 3 |
sector 4 |
sector 5 |
sector 6 |
|
u |
u |
u |
u |
u |
u |
||
|
u |
u |
u |
u |
u |
u |
||
|
u |
u |
u |
u |
u |
u |
||
|
u |
u |
u |
u |
u |
u |
||
|
u |
u |
u |
u |
u |
u |
||
|
u |
u |
u |
u |
u |
u |
Vectorii de comutatie activi: u1 = (1 0 0); u2 = (1 1 0); u3 = (0 1 0); u4 = (0 1 1); u5 = (0 0 1); u6 = (1 0 1). Vectorii de comutatie zero: u7 = (1 1 1); u8 = (0 0 0).
Alegerea latimii benzilor de histerezis are efecte importante, deoarece o valoare prea mica are efectul pierderii comenzii, spre exemplu fluxul statoric poate depasi valorile impuse prin banda de toleranta (latimea careia este 2.s). Durata starilor zero influenteaza direct oscilatiile cuplului.
Tabela
de comutatie optima (tab. 5.1) necesita cunoasterea
fazorului spatial al fluxului statoric, deoarece trebuie cunoscut in care
sector este fazorul spatial al fluxului statoric. Pentru aceasta sunt
necesare unghiurile (1), (2), , (6) aratate in
fig. 5.4. Deoarece ![]() unghiul fluxului
statoric (s) poate fi determinat prin folosirea valorilor
estimate ale fluxului in axa directa si in axa in cuadratura a
sistemului de referinta statoric (sd, sq);
astfel:
unghiul fluxului
statoric (s) poate fi determinat prin folosirea valorilor
estimate ale fluxului in axa directa si in axa in cuadratura a
sistemului de referinta statoric (sd, sq);
astfel:
![]() (5.8)
(5.8)
Se poate de asemenea folosi expresia:
![]() (5.8)
(5.8)
Se poate deci folosi unghiul s pentru a obtine unghiurile (1), (2), , etc. Totusi este posibil sa eliminam necesitatea folosirii functiilor trigonometrice, deoarece nu trebuie cunoscuta pozitia precisa a fazorului spatial al fluxului statoric ci numai sectorul (numarul) in care este pozitionat fazorul spatial al fluxului statoric [21]. Aceasta informatie se poate obtine comod - numai prin considerarea semnelor diferitelor componente ale fluxului statoric - si aceasta permite o implementare simpla care necesita numai utilizarea comparatoarelor. Pentru aceasta ar trebui considerat ca, de exemplu, in sectorul 1, sd > 0, dar - deoarece in sectorul 1 sq poate fi atat pozitiv cat si negativ - semnul lui sq nu ne va da nici o informatie utila asupra pozitiei fazorului spatial al fluxului statoric in sectorul 1.
Totusi, in locul lui sq este posibil sa folosim fluxul statoric din faza bs (sb) si conform figurii 5.6 rezulta ca sb < 0 daca s este in primul sector (in punctul P1 unde are valoarea s1). In acelasi mod, daca s este in sectorul 2, atunci sd > 0, sq > 0 si sb > 0, etc. Rezultatele sunt sintetizate in tabelul
Tabelul Selectia sectorului fazorului spatial al fluxului statoric.
|
|
Sectoa-re |
sector 1 |
sector 2 |
sector 3 |
sector 4 |
sector 5 |
sector 6 |
|
Semnul fluxului | |||||||
|
Semnul lui sd | |||||||
|
Semnul lui sq |
(NU) |
(NU) | |||||
|
Semnul lui sb | |||||||
![]() Semnul lui sbsemnul
lui .
Semnul lui sbsemnul
lui .
NU = nu este util.
Se poate observa ca semnul lui sq nu da o informatie utila in sectorul 1 si 4 deoarece in ambele sectoare semnul poate fi pozitiv (+) sau negativ (-). Conform fig. 5.6 si tab. 5.2 se observa ca, pentru sd trei semne plus (in sectoarele 6, 1 si 2) sunt urmate de trei semne minus (in sectoarele 3, 4 si 5) si asemanator, pentru sb, trei semne plus (in sectoarele 2, 3 si 4) sunt urmate de trei semne minus (in sectoarele 5, 6 si 1).
Trebuie observat ca pentru selectarea sectorului potrivit, calculul lui s - prin utilizarea ecuatiei 5.8, a ecuatiei 5.9 sau a ecuatiei 5.10 - poate fi evitat prin utilizarea altei tehnici, in care se determina mai intai semnele lui sd si sq. Acestea dau informatii asupra cadranului in care este localizat fazorul spatial al fluxului statoric. Sunt patru cadrane si fiecare cadran (fig. 5.6) are o deschidere de 900: primul cadran incepe de la axa d si se intinde pana la axa q; al doilea incepe de la axa q si se intinde pana la axa negativa d, etc. Deoarece fiecare cadran contine numai un sector intreg si jumatate din alt sector, exista astfel doua posibile sectoare (in cadran) incat sectorul precis in care este localizat s se poate obtine folosind raportul sq / sd. Este deci posibil de a folosi si alte tehnici care sa minimizeze calculul.

Aplicarea vectorilor de
comutatie din tabelul 5.2 conduc la rezultate excelente cand viteza
masinii nu este prea redusa. Totusi, la viteze foarte reduse
controlul fluxului poate fi pierdut. De exemplu, pot apare probleme la pornirea
masinii. In acest caz, desi la t = 0 se aplica un flux impus (de
referinta) constant si la t > t1 se aplica un
cuplu treapta impus, modulul fazorului spatial al fluxului statoric
real va fi zero pana la t = t1, si chiar dupa t1,
astfel ca cuplul nu va atinge valoarea impusa si va varia.
Astfel in loc de a avea o traiectorie circulara corespunzatoare
fluxului impus constant, va fi un loc geometric simetric cu sase laturi,
(nu un hexagon simetric), unde in timpul 1/6 dintr-un ciclu modulul fazorului
spatial al fluxului statoric se schimba (intr-un
'colt' este maxim, apoi descreste si apoi atinge
valoarea maxima din nou in urmatorul 'colt').
Problemele se refera la utilizarea nepotrivita a vectorilor de
comutatie a tensiunii in regiunea vitezei reduse. Schemele DTC
imbunatatite, incuzand schemele de selectie
imbunatatita a vectorului de comutatie si
schemele de selectie predictiva a vectorului de comutatie, se vor
discuta ulterior.
3. Selectia predictiva a vectorului de comutatie
3.1. Scheme predictive
Intr-o actionare cu motor asincron cu controlul direct al cuplului folosind tabelul 5.2 se obtine un raspuns lent la pornire si la o schimbare a valorii impuse (de referinta) a flulxului statoric si a cuplului electromagnetic. Cu toate ca vectorii de comutatie ai tensiunii sunt determinati de pozitia fluxului statoric si de erorile cuplului electromagnetic si a modulului fazorului spatial al fluxului statoric, nu se pot distinge erorile mari de cele mici. Astfel, alegerea vectorilor de comutatie pentru erori mari (de exemplu in timpul pornirii sau in timpul schimbarii treapta a cuplului) este la fel cu alegerea vectorilor de comutatie pentru functionarea normala, cand erorile sunt mici. Totusi este posibil sa alegem vectorii de comutatie in concordanta cu domeniul erorilor (si pozitia fazorului spatial al fluxului statoric). In acest caz se pot creste raspunsurile la pornire si la schimbarea valorii de referinta a fluxului statoric si a cuplului electromagnetic. Exista diferite solutii posibile, de exemplu este posibil sa folosim un sistem cu logica fuzzy. In acest sistem se utilizeaza, in timpul pornirii, acele stari de comutatie care dau cresterea cea mai rapida a fluxului statoric (in timp ce schimbarea cuplului este mica). Cand eroarea fluxului statoric devine mica, se aleg acele stari de comutatie care dau cresterea mai rapida a cuplului electromagnetic [28].
Trebuie observat ca pe langa utilizarea startegiei de selectie a vectorului de comutatie bazata pe logica fuzzy este posibil sa obtinem imbunatatiri prin folosirea unei scheme bazata pe inteligenta ne-artificiala, in care erorile fluxului statoric si cuplului electromagnetic nu se cuantizeaza in doua sau trei nivele si unde se folosesc mai mult de sase sectoare ale fluxului statoric.
Este posibil sa implementam scheme de actionare cu controlul direct al cuplului in care vectorii de comutatie ai tensiunii ceruti se obtin prin algoritmi predictivi. Pentru aceasta se utilizeaza un model matematic corespunzator al masinii asincrone iar cuplul electromagnetic se estimeaza pentru fiecare perioada de esantionare pentru toate starile posibile ale invertorului. Apoi, algoritmul predictiv selectioneaza starile de comutatie ale invertorului care dau deviatia minima dintre cuplul prezis si cuplul impus. Deoarece exista multe posibilitati, pentru modelul matematic care se va utiliza in continuare se discuta numai conceptele principale [21].
Pentru schema de estimare predictiva a vectorului de comutatie se poate obtine un model matematic convenabil al masinii asincrone considerand ecuatiile de tensiune ale statorului si rotorului si expresia cuplului electromagnetic in cazul unui sistem de referinta comun, atasat fluxului rotoric. Pentru aceasta tinem seama de curentul de magnetizare imr corespunzator fluxului rotoric (rel. 4.1).

Ecuatiile generale ale
tensiunilor (rel. 2.15 si 2.18) se obtin conform fig. 5.7. Pentru
stator, relatia (2.15) devine:
![]()
iar fluxul statoric (rel. 2.54) va fi:
![]()
Din aceste ecuatii rezulta:
![]()
(5.11)
Conform fig. 5.7, imr este colinear cu d r si deci:
![]()
Din relatia (4.5) rezulta:
![]() (5.12)
(5.12)
Inlocuind (5.12) in (5.11) se obtine:
![]()
(5.13)
unde:

este inductanta tranzitorie a statorului in sistemul de axe d r - q r si
![]()
Pentru rotorul in scurtcircuit, relatia (2.18) devine:
![]() (5.13
a)
(5.13
a)
iar fluxul rotoric (rel. 2.54) va fi:
![]() (5.13
b)
(5.13
b)
Din aceste ecuatii rezulta:
![]() , (5.14)
, (5.14)
unde:
![]()
este
Pentru usurinta vom nota marimile raportate la sistemul de axe atasat fluxului rotoric cu prim ' ' '. Ecuatiile (5.13) si (5.14) se vor scrie:
![]() (5.15)
(5.15)
![]() (5.16)
(5.16)
La acestea se mai adauga ecuatia cuplului electromagnetic:
![]() (5.17)
(5.17)
Este
posibil sa combinam aceste ecuatii intr-o singura
ecuatie (vectoriala) pentru fazorul spatial al tensiunii
statorice, exprimat in sistemul de referinta fix d - q, care sa
contina cuplul electromagnetic, modulul spatial al fluxului
rotoric, viteza rotorului si parametrii masinii. Presupunand ca
intr-un interval de timp de esantionare viteza a rotorului este ![]() ). Astfel se poate determina, prin folosirea modulatiei
fazorului spatial, starea corespunzatoare a invertorului.
). Astfel se poate determina, prin folosirea modulatiei
fazorului spatial, starea corespunzatoare a invertorului.
Este
de asemenea posibil sa determinam starea necesara a vectorilor
de comutatie a tensiunii prin utilizarea unei scheme predictive in care
exista reglarea deadbeat a
cuplului electromagnetic si fluxului statoric pe un ciclu constant de
comutatie. In acest scop se calculeaza fazorul spatial al
tensiunii statorice necesare, pentru a regla cuplul electromagnetic si
fazorul spatial al fluxului statoric, ciclu cu ciclu, utilizand eroarea
cuplului electromagnetic si erorile fluxului statoric din ciclul precedent
si de asemenea tensiunea electromotoare a masinii asincrone. Unul din
avantajele acestui algoritm este acela ca va conduce la o
frecventa de comutatie
3.2. Baza matematica si fizica a algoritmului predictiv in regim stationar
1. Estimarea variatiei cuplului pe o perioada de esantionare
Variatia cuplului electromagnetic pe o perioada care este o jumatate a perioadei de comutatie se obtine pe baza componentelor fluxului statoric, a valorilor impuse (de referinta) ale componentelor tensiunii statorice si a componentelor t.e.m. In acest scop ecuatia tensiunii statorice a masinii asincrone se utilizeaza impreuna cu expresia cuplului electromagnetic. In contrast cu schema predictiva generala, descrisa anterior, pentru determinarea vectorilor de comutatie ai tensiunii nu se utilizeaza ecuatia de tensiune a rotorului, deoarece ecuatia de tensiune a statorului se exprima pe baza t.e.m. (care contine implicit fluxul rotoric) si a cuplului electromagnetic obtinut pe baza t.e.m. [21]. In sistem de coordonate fix, statoric, d - q ecuatia tensiunii statorice va fi:
![]()
si tinand seama ca:
![]() ,
,
unde i'r este fazorul spatial al curentului rotoric scris in sistemul de coordonate d q (a se vedea 1) rezulta:
![]() (5.18)
(5.18)
Definim prin imr curentul de magnetizare corespunzator fluxului rotoric:
![]() (5.19)
(5.19)
unde s-a tinut seama de faptul ca:
![]()
iar:
![]()
este coeficientul de scapari al rotorului. Inlocuind i'r din rel. (5.19) in ecuatia (5.18) obtinem:
 .
.
Daca se noteaza prin:

coeficientul de scapari, ecuatia tensiunii statorice devine:
![]()
Notam
prin ![]() inductanta
tranzitorie a statorului si rezulta:
inductanta
tranzitorie a statorului si rezulta:
![]()
sau:
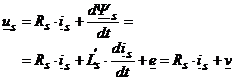 (5.20)
(5.20)
unde
e este fazorul spatial al t.e.m. iar ![]() v este tensiunea pe inductanta tranzitorie a
statorului (L's).
v este tensiunea pe inductanta tranzitorie a
statorului (L's).
Astfel, daca se neglijeaza caderea de tensiune rezistiva a statorului, este posibil sa se estimeze componentele t.e.m. dupa cele doua axe:
![]() (5.21)
(5.21)
Trebuie observat ca presupunand ca s si e sunt marimi sinusoidale atunci:
![]()
unde 1 este frecventa statorica si se poate estima simplu folosind:

Aceasta
poate fi dovedita considerand ecuatia ![]() si inlocuind d/dt cu j.1.
si inlocuind d/dt cu j.1.
De asemenea, din ecuatia (5.20) daca se neglijeaza caderea de tensiune rezistiva, viteza de variatie a fazorului spatial al curentului statoric este:
 (5.22)
(5.22)
Daca
Ts este timpul, care este
egal cu jumatatea perioadei de comutatie, si se presupune
ca acesta este suficient de mic, atunci ![]() si variatia
curentului statoric se obtine din ecuatia (5.22) ca:
si variatia
curentului statoric se obtine din ecuatia (5.22) ca:
![]() (5.23)
(5.23)
Presupunand
ca
![]()
si considerand ecuatia (3) se obtine:
 (5.24)
(5.24)
Se
poate vedea ca variatia cuplului electromagnetic intr-o perioada
Ts se poate obtine din tensiunea statorica impusa (de
referinta) - care este de acum ![]() deoarece s-a neglijat
caderea de tensiune rezistiva - si de asemenea din fazorul e. Utilizand forma celor
doua axe a ecuatiei (5.24) si considerand:
deoarece s-a neglijat
caderea de tensiune rezistiva - si de asemenea din fazorul e. Utilizand forma celor
doua axe a ecuatiei (5.24) si considerand:
![]()
se obtine:
![]() (5.25)
(5.25)
Din ecuatia (5.25) valoarea tensiunii de referinta (impuse) in axa q este:
 (5.26)
(5.26)
unde:
 (5.27)
(5.27)
2. Tensiunile statorice necesare pentru reglarea deadbeat
Variatia
fluxului statoric se poate obtine din ecuatia (5.20) neglijand
caderea de tensiune rezistiva (care este o presupunere valabila
daca frecventa statorica este peste cativa Hz) si
considerand ![]()
![]() (5.28)
(5.28)
Deoarece![]() , considerand ecuatia (5.28) rezulta ca:
, considerand ecuatia (5.28) rezulta ca:
![]() (5.29)
(5.29)
unde
tn este inceputul celei de-a n
- a perioade Ts si ![]() este fazorul
spatial al fluxului statoric la inceputul perioadei de esantionare
(componentele fluxului statoric se cunosc deoarece ele se determina prin
integrarea tensiunii statorice necesare).
este fazorul
spatial al fluxului statoric la inceputul perioadei de esantionare
(componentele fluxului statoric se cunosc deoarece ele se determina prin
integrarea tensiunii statorice necesare).
Ecuatia (5.29) se poate folosi pentru obtinerea tensiunii statorice necesare pentru reglarea deadbeat a fluxului statoric. Folosind forma celor doua axe a ecuatiei (5.29),
![]() (5.30)
(5.30)
unde
sd si sq sunt componentele fluxului
statoric la inceputul celei de-a n -
a perioade de esantionare. Astfel, componentele tensiunii statorice impuse
(de referinta), ![]() si
si ![]() , se pot obtine din ecuatiile (5.26) si
(5.30). Inlocuind expresia (5.26) in (5.30) se obtine o ecuatie de
gradul al doilea in care necunoscuta este
, se pot obtine din ecuatiile (5.26) si
(5.30). Inlocuind expresia (5.26) in (5.30) se obtine o ecuatie de
gradul al doilea in care necunoscuta este ![]() ,
,

(5.31)
Ecuatia
(5.31) conduce la doua solutii pentru ![]() , dar se alege solutia cu cea mai mica valoare
absoluta, deoarece aceasta corespunde celei mai mici tensiuni statorice,
dupa axa d, necesara de a aduce fluxul statoric si cuplul
electromagnetic la valorile lor de referinta (impuse). Daca
valoarea obtinuta
, dar se alege solutia cu cea mai mica valoare
absoluta, deoarece aceasta corespunde celei mai mici tensiuni statorice,
dupa axa d, necesara de a aduce fluxul statoric si cuplul
electromagnetic la valorile lor de referinta (impuse). Daca
valoarea obtinuta ![]() se substituie in
ecuatia (5.26) se obtine in final
se substituie in
ecuatia (5.26) se obtine in final ![]() . Astfel se obtine
. Astfel se obtine ![]() (care corespunde
fazorului spatial al tensiunii de referinta, daca se
neglijeaza caderea de tensiune rezistiva statorica). De
aceea fazorul spatial al tensiunii statorice de referinta (care
include si efectul caderii de tensiune rezistive statorice) se
obtine ca:
(care corespunde
fazorului spatial al tensiunii de referinta, daca se
neglijeaza caderea de tensiune rezistiva statorica). De
aceea fazorul spatial al tensiunii statorice de referinta (care
include si efectul caderii de tensiune rezistive statorice) se
obtine ca:
![]() (5.32)
(5.32)
In
ecuatia (5.32) caderea de tensiune rezistiva din ciclul
precedent Rs.is(tn) se adauga termenului ![]() . In orice caz, aceasta se justifica cand - asa cum
s-a discutat mai inainte - variatia curentului statoric se presupune a fi
liniara in perioada Ts (cand caderea de tensiune
rezistiva este mica in comparatie cu caderea de tensiune pe
inductanta tranzitorie a statorului).
. In orice caz, aceasta se justifica cand - asa cum
s-a discutat mai inainte - variatia curentului statoric se presupune a fi
liniara in perioada Ts (cand caderea de tensiune
rezistiva este mica in comparatie cu caderea de tensiune pe
inductanta tranzitorie a statorului).
3. Determinarea starii de comutatie a invertorului in regim stationar (vectorul spatial PWM)
Starea
potrivita de comutatie a invertorului se determina folosind
modulatia in latime a vectorului spatial (PWM). De aceea ![]() (definit de
ecuatia 5.32) se foloseste pentru selectarea optima a vectorilor
de comutatie a tensiunii in asa fel incat se selecteaza doi
vectori de comutatie (
(definit de
ecuatia 5.32) se foloseste pentru selectarea optima a vectorilor
de comutatie a tensiunii in asa fel incat se selecteaza doi
vectori de comutatie (![]() , si se determina timpul in care se aplica
acesti vectori (tk, tk+1) din:
, si se determina timpul in care se aplica
acesti vectori (tk, tk+1) din:
![]() (5.33)
(5.33)
In ecuatia (5.33):
![]() (5.34)
(5.34)
unde
Ts este timpul de esantionare. Ecuatia (5.33) rezulta
din faptul ca media in timp a celor trei stari de comutatie
(doua stari active si o stare zero) in timpul intervalului de
esantionare este egala cu vectorul spatial al tensiunii de
referinta. Vectorii de comutatie si vectorul tensiunii de
referinta sunt constanti intr-un ciclu de comutatie. In
ecuatia (5.33)
 (5.35)
(5.35)
unde
E este tesniunea continua din circuitul intermediar, k = 1, 2, , 6
corespunde vectorilor activi de comutatie a tensiunii (diferiti de
zero) si k = 7, 8 corespunde celor doi vectori zero. Daca se
inlocuieste ecuatia (5.35) in ecuatia (5.33) si
ecuatia rezultanta se rezolva in partile sale reale
si imaginare, atunci se pot determina tk si tk+1.
Astfel, folosind ![]() se obtin:
se obtin:
 , (5.36)
, (5.36)
![]() , (5.37)
, (5.37)
sau
utilizand coordonatele polare  :
:
 , (5.38)
, (5.38)
 , (5.39)
, (5.39)
unde a este indicele de modulatie:
![]() . (5.40)
. (5.40)
Timpul in care se selecteaza cel mai potrivit vector de comutatie zero este:
![]() (5.41)
(5.41)
Comutatia din starea zero in doua stari adiacente implica fiecare ramura a invertorului o data, astfel ca Ts este o jumatate de perioada a frecventei de comutatie. De aceea fluxul statoric si cuplul electromagnetic se comanda de doua ori pe frecventa de comutatie. In plus, cand se foloseste acest algoritm de reglare, se reduc oscilatiile curentilor statorici.
In
conditii tranzitorii nu este posibila o reglare deadbeat. Aceasta se
datoreste faptului ca, in acest caz, nu este suficienta tensiune
de c.c. in circuitul intermediar pentru a produce o schimbare adecvata in
cuplul electromagnetic si/sau in fluxul statoric pentru a obtine o
reglare deadbeat. Din ecuatiile (5.34), (5.36) si (5.37) urmeaza
ca atunci cand exista o modificare a cuplului electromagnetic
si/sau o modificare a fluxului statoric (de exemplu schimbari in
treapta), erorile cuplului elecromagnetic si fluxului statoric sunt
mari intr-o perioada de comutatie si astfel se obtine tk
+ tk+1 > Ts. Aceasta inseamna ca ![]() este prea mare pentru
a fi sintetizata intr-o singura perioada de comutatie
si prin urmare trebuie sa se foloseasca o tehnica
alternativa de reglare. Pentru a rezuma, schema deadbeat prezentata este potrivita pentru determinarea
vectorilor de comutatie in regim stationar al
actionarii si are
avantajul ca frecventa de comutatie este
este prea mare pentru
a fi sintetizata intr-o singura perioada de comutatie
si prin urmare trebuie sa se foloseasca o tehnica
alternativa de reglare. Pentru a rezuma, schema deadbeat prezentata este potrivita pentru determinarea
vectorilor de comutatie in regim stationar al
actionarii si are
avantajul ca frecventa de comutatie este
4. Algoritm de reglare predictiva in regim stationar
In continuare se descrie un algoritm predictiv in opt etape (pentru a n - a perioada arbitrara de esantionare Ts).
Etapa 1 - a. Estimarea fluxului statoric
In actionarea cu motor asincron cu controlul direct al cuplului, componentele fluxului statoric se vor estima tinand seama de doua motive. Primul motiv este ca aceste componente sunt necesare in tabela de selectie optima a vectorului de comutatie, aspect discutat anterior. Al doilea motiv este acela ca ele sunt de asemenea necesare pentru estimarea cuplului electromagnetic. Trebuie observat ca estimarea, in general, rezulta direct din ecuatia tensiunii statorice in sistemul de referinta fix, statoric, d - q astfel:
![]() (5.42)
(5.42)
![]() (5.43)
(5.43)
si cum se va arata mai jos:
![]() (5.44)
(5.44)
Daca se utilizeaza fazorii spatiali, atunci:
![]()
![]()
unde
![]() si
si ![]() .
.
Totusi,
deoarece ![]() se obtine,
tninand seama de ecuatia (5.44):
se obtine,
tninand seama de ecuatia (5.44):
![]() .
.
Nu
este necesar sa folosim trei senzori pentru tensiunile statorice si
trei senzori pentru curentii statorici deoarece este posibil, considerand ![]() si
si ![]() , sa obtinem usd si usq
prin monitorizarea a doua tensiuni de linie (de exemplu uba, uac)
si sa obtinem isd si isq prin
monitorizarea a doi curenti (isa, isb). Astfel:
, sa obtinem usd si usq
prin monitorizarea a doua tensiuni de linie (de exemplu uba, uac)
si sa obtinem isd si isq prin
monitorizarea a doi curenti (isa, isb). Astfel:
![]()
Din
ecuatia (5.44) rezulta ca semnul fluxului sb
se poate obtine din examinarea semnului fluxului ![]() (fizic aceasta
corespunde dublului fluxului statoric in faza bs). Este important de
observat ca performantele actionarii cu controlul direct al
cuplului folosind ecuatia (5.42) si (5.43) va depinde in mare
masura de acuratetea estimarii componentelor fluxului
statoric si aceasta depinde de acuratetea monitorizarii
tensiunilor si curentilor si de asemenea de acuratetea
tehnicii de integrare. Totusi, pot aparea erori in monitorizarea
tensiunilor statorice si a curentilor statorici datorita
urmatorilor factori: defazaj in valorile masurate (datorita
senzorilor utilizati), erori datorita factorilor de conversie si
castigului, abateri reziduale in sistemul de masurare, erori in
sistemul digital etc. De asemenea trebuie folosita o valoare corecta
pentru rezistenta statorica.
(fizic aceasta
corespunde dublului fluxului statoric in faza bs). Este important de
observat ca performantele actionarii cu controlul direct al
cuplului folosind ecuatia (5.42) si (5.43) va depinde in mare
masura de acuratetea estimarii componentelor fluxului
statoric si aceasta depinde de acuratetea monitorizarii
tensiunilor si curentilor si de asemenea de acuratetea
tehnicii de integrare. Totusi, pot aparea erori in monitorizarea
tensiunilor statorice si a curentilor statorici datorita
urmatorilor factori: defazaj in valorile masurate (datorita
senzorilor utilizati), erori datorita factorilor de conversie si
castigului, abateri reziduale in sistemul de masurare, erori in
sistemul digital etc. De asemenea trebuie folosita o valoare corecta
pentru rezistenta statorica.
Pentru estimarea corecta a fluxului, rezistenta statorica trebuie adaptata schimbarilor de temperatura. Integrarea poate deveni problematica la frecvente joase, cand tensiunile statorice devin foarte mici si sunt determinate de caderea de tensiune rezistiva. La frecvente mici trebuie considerata caderea de tensiune pe invertor. Aceasta este o problema tipica asociata estimatoarelor de flux in bucla deschisa, folosite in alte actionari de c.a. care utilizeaza curentii si tensiunile la borne.
Compensarea derivei este de asemenea un factor important in implementarea practica a integrarii, deoarece poate produce erori mari in pozitia fluxului. In implementarea analogica sursa derivei este deriva termica a integratoarelor analogice. Daca se foloseste un estimator de viteza in bucla deschisa in controlul direct al cuplului motorului asincron, care utilizeaza componentele estimate ale fluxului statoric, viteza se determina folosind pozitia fazorului spatial al fluxului, astfel ca o deriva in fazorul spatial al fluxului va cauza valori incorecte si oscilatorii ale vitezei. Un estimator de flux in bucla deschisa va lucra bine la 1 - 2 Hz dar sub aceste valori se folosesc tehnici speciale.
Daca tensiunile statorice nu pot fi monitorizate, atunci este posibil sa reconstruim tensiunile statorice din monitorizarea tensiunii din circuitul intermediar de c.c. al invertorului si din starile de comutatie ale invertorului (a se vedea subcap. 5.4). Este posibil sa utilizam orice scheme de estimare a fluxului: aplicarea filtrelor trece-jos, a elementelor de intarziere de ordinul intai, a observatoarelor (Luenberger, Kalman), a sistemului de reglare adaptiva cu model de referinta etc.
Etapa a 2 - a. Estimarea componentelor t.e.m. din fluxuri si curenti
Componentele t.e.m. (ed, eq) se estimeaza folosind ecuatia (5.21) unde:
![]() .
.
Etapa a 3 - a. Estimarea cuplului electromagnetic din flux si curenti
Valoarea reala a cuplului electromagnetic se estimeaza cu:
![]() .
.
Etapa a 4 - a. Estimarea variatiei cuplului electromagnetic
![]() .
.
Etapa a 5 - a. Estimarea
tensiunii statorice necesare de referinta in axa d (![]() ) presupunand Rs = 0
) presupunand Rs = 0
Estimarea
![]() se face utilizand
relatia (5.31), tinand seama de ecuatia (5.27) si alegand
solutia cu cea mai mica valoare absoluta.
se face utilizand
relatia (5.31), tinand seama de ecuatia (5.27) si alegand
solutia cu cea mai mica valoare absoluta.
Etapa a 6 - a. Estimarea
tensiunii statorice necesare de referinta in axa q (![]() ) presupunand Rs = 0
) presupunand Rs = 0
Estimarea
![]() se face utilizand
relatia (5.26) si tinand seama de (5.27).
se face utilizand
relatia (5.26) si tinand seama de (5.27).
Etapa a 7 - a. Estimarea
fazorului spatial al tensiunii de referinta necesare ![]() (adaugand
factorul de corectie datorita lui Rs ≠ 0)
(adaugand
factorul de corectie datorita lui Rs ≠ 0)
Estimarea fazorului spatial al tensiunii de referinta se face cu relatia (5.32) astfel:
 .
.
Etapa a 8 - a. Estimarea timpilor de aplicare ai vectorilor adiacenti si ai vectorilor zero (tk, tk+1 si t0)
Timpii de aplicare ai vectorilor adiacenti (tk, tk+1) se estimeaza cu ecuatiile (5.36) si (5.37) sau cu ecuatiile (5.38), (5.39) si (5.40). Timpul de aplicare al vectorului de comutatie zero (t0) se determina cu ecuatia (5.41). Daca exista o solutie, atunci starile de comutatie si intervalele de comutatie constituie baza comenzii invertorului. Daca nu exista solutie (deoarece nu este posibil de a avea o reglare deadbeat a fluxului statoric si cuplului electromagnetic), atunci se va proceda conform metodei descrise in continuare.
3.3. Reglarea predictiva in regim tranzitoriu
In cele ce urmeaza se discuta strategia de reglare predictiva (alegerea vectorului de comutatie) pentru a se utiliza in conditii tranzitorii. Daca exista o modificare a referintei cuplului electromagnetic (de exemplu schimbarea treapta), atunci regulatorul trebuie sa conduca cuplul electromagnetic in directia necesara (pentru a reduce eroarea cuplului in perioada Ts) in timp ce se mentine reglarea deadbeat a fluxului statoric. Daca exista o modificare a referintei fluxului statoric, atunci fluxul statoric trebuie condus in directia referintei sale in timp ce se mentine reglarea deadbeat a cuplului electromagnetic. In aceasta situatie, alegerea vectorilor potriviti de comutatie poate fi realizata prin considerarea mai intai a pozitiei fazorului spatial al fluxului statoric (fata de axa d a sistemului de referinta fix), s (fig. 5.2) si apoi se considera sensul cuplului electromagnetic sau eroarea fluxului statoric. Aceasta se va discuta in continuare in detaliu.
Mai intai se presupune o schimbare a referintei cuplului cand cuplul electromagnetic nu poate fi condus spre valoarea sa de referinta intr-o singura perioada Ts (adica nu este posibila reglarea deadbeat a cuplului). Aceasta este cel mai important caz care apare cel mai frecvent si in general nu se cere o schimbare in treapta a fluxului statoric. In cele mai multe cazuri fluxul se schimba numai in domeniul slabirii campului. Totusi, in acest mod de functionare, cand fluxul incepe sa scada, exista o variatie aproape liniara si deci el variaza continuu. Astfel, pentru a obtine o schema simplificata predictiva de alegere a vectorului de comutatie se poate neglija modificarea simultana a cuplului si fluxului [21].
Pentru cazul cand exista numai o schimbare a cuplului, vectorii de comutatie se aleg a priori in asa fel incat sa conduca cuplul in directia dorita, permitand insa reglarea deadbeat a fluxului statoric. Daca, de exemplu, fazorul spatial al fluxului statoric se afla in sectorul 1 aratat in fig. 5.5, care are o deschidere de la - 300 la 300 [unghiul (1)], atunci vectorii u2 si u3 produc cresterea cuplului electromagnetic si permit reglarea fluxului (u2 creste fluxul iar u3 scade fluxul). Similar, u5 si u6 produc o scadere a cuplului electromagnetic si permit reglarea fluxului (u5 scade fluxul iar u6 creste fluxul). Astfel u2 si u3 (care corespund starilor de comutatie 2 si 3) pot fi folositi pentru a regla fluxul statoric la valoarea sa de referinta (impusa) intr-o perioada Ts, in timp ce cuplul creste continuu pe intregul interval. Prin urmare este posibil sa alcatuim un tabel de selectie a vectorilor pentru regimul tranzitoriu prin care se aleg doi vectori [vectorii k si (k + 1)] folosind eroarea de cuplu si numarul sectorului n = 1, 2, ,,,, 6 (unde este localizat fazorul spatial al fluxului statoric). Aceasta situatie este aratata in tabelul 5.3. Sectorul unde este localizat un fazor spatial al fluxului statoric poate fi determinat din pozitia fazorului spatial al fluxului (a se vedea discutia de la paragraful 2).
In tabelul 5.3, k si k + 1 inseamna starea de comutatie cu numarul de ordine k respectiv k + 1. In exemplul analizat k corespunde vectorului u2 (starea a 2 - a de comutatie si k + 1 corespunde vectorului u3 starea a 3 - a de comutatie) pentru cresterea cuplului electromagnetic. Pentru scaderea cuplului (linia a 2 - a din tabelul 5.3) k ar corespunde vectorului u5 iar k + 1 vectorului u6.
Astfel prin folosirea vectorilor de comutatie selectati uk uk+1, fluxul statoric este reglat in maniera deadbeat, similara cu cea data de ecuatia (5.29); astfel:
![]() , (5.45)
, (5.45)
unde
pe durata tk se aplica vectorul de comutatie
In regim tranzitoriu nu se folosesc vectorii zero, deoarece se doreste conducerea cuplului electromagnetic intr-o directie in modul cel mai rapid in timpul perioadei de comutatie. Astfel t0 = 0 si din ecuatia (5.41) rezulta ca:
![]() . (5.46)
. (5.46)
Tabelul 5.3. Selectia vectorului de comutatie al tensiunii cand exista o schimbare a referintei cuplului electromagnetic.
|
sgn (me - me*) |
k |
k + 1 |
|
|||||||||||||||||||||||||||
|
sect. |
sect. |
sect. |
sect. |
sect. |
sect. |
sect. |
sect. |
sect. |
sect. |
sect. |
sect. |
||||||||||||||||||
|
u |
u |
u |
u |
u |
u |
u |
u |
u |
u |
u |
u |
|
|||||||||||||||||
|
u |
u |
u |
u |
u |
u |
u |
u |
u |
u |
u |
u |
|
|||||||||||||||||
Trebuie
observat ca omiterea starilor zero in timpul comutatiei intre
starile adiacente este echivalenta cu scaderea pulsului intr-un
PWM sinusoidal conventional. Pentru o valoare data a lui ![]() , ecuatiile (5.45) si (5.46) pot fi rezolvate in
raport cu tk si tk + 1. Astfel, prin aplicarea
vectorilor de comutatie potriviti pe durata potrivita, se
regleaza fluxul statoric spre valoarea sa de referinta si cuplul
electromagnetic este condus continuu spre valoarea sa dorita in
directia potrivita, cu tensiune maxima aplicata
invertorului (datorita lui t0 = 0, tensiunea de
referinta se mentine in limita locului geometric hexagonal;
astfel tensiunea de iesire a invertorului este maxima).
, ecuatiile (5.45) si (5.46) pot fi rezolvate in
raport cu tk si tk + 1. Astfel, prin aplicarea
vectorilor de comutatie potriviti pe durata potrivita, se
regleaza fluxul statoric spre valoarea sa de referinta si cuplul
electromagnetic este condus continuu spre valoarea sa dorita in
directia potrivita, cu tensiune maxima aplicata
invertorului (datorita lui t0 = 0, tensiunea de
referinta se mentine in limita locului geometric hexagonal;
astfel tensiunea de iesire a invertorului este maxima).
Daca
se considera al doilea caz, cand exista o schimbare a referintei fluxului statoric (adica fluxul
statoric nu poate fi condus spre valoarea sa de referinta intr-o
singura perioada Ts), atunci din nou selectia
vectorului de tensiune se face a priori.
In acest caz, daca de exemplu, fazorul spatial al fluxului statoric
este in sectorul 1 (fig. 5.5),
u1 si u2 cresc fluxul iar u3
si u4 descresc fluxul, etc. Selectia vectorilor de
comutatie potriviti este aratata in tabelul 5.4. Astfel
prin selectia vectorilor de comutatie
![]() . (5.47)
. (5.47)
Tabelul 5.4. Selectia vectorului de comutatie al tensiunii cand exista o schimbare a referintei fluxului statoric.
|
sgn (s - s*) |
k |
k + 1 |
|
|||||||||||||||||||||||||||
|
sect. |
sect. |
sect. |
sect. |
sect. |
sect. |
sect. |
sect. |
sect. |
sect. |
sect. |
sect. |
||||||||||||||||||
|
u |
u |
u |
u |
u |
u |
u |
u |
u |
u |
u |
u |
|
|||||||||||||||||
|
u |
u |
u |
u |
u |
u |
u |
u |
u |
u |
u |
u |
|
|||||||||||||||||
Ecuatiile
(5.46) si (5.47) produc valorile necesare tk si tk +
1. Astfel daca vectorul de comutatie selectat
In sfarsit se considera a treia conditie: cazul cand exista o schimbare a fluxului statoric si cuplului electromagnetic. In acest caz se selecteaza o singura conditie pentru intreaga perioada de comutatie, care conduce ambele marimi, fluxul statoric si cuplul electromagnetic, in directiile dorite cat mai rapid posibil. De exemplu, daca fazorul fluxului statoric este in sectorul 1 (fig. 5.5) si ambele marimi - fluxul si cuplul - trebuie sa creasca, atunci, prin considerarea celor sase vectori de comutatie, se selecteaza u2. Daca fluxul trebuie sa creasca si cuplul trebuie sa scada atunci se selecteaza u6, etc. Selectia vectorilor de comutatie este data in tabelul 5.5.
Tabelul 5.5. Selectia vectorului de comutatie al tensiunii cand se modifica ambele marimi: fluxul statoric si cuplul electromagnetic.
|
sgn (me - me*) |
sgn (s - s*) |
sect. |
sect. |
sect. |
sect. |
sect. |
sect. |
||||||||
|
u |
u |
u |
u |
u |
u |
|
||||||||||
|
u |
u |
u |
u |
u |
u |
|
||||||||||
|
u |
u |
u |
u |
u |
u |
|
||||||||||
|
u |
u |
u |
u |
u |
u |
|
||||||||||
Evident aceasta este in acord cu parti componente din tabelul 5.1 prezentat in paragraful 2. Astfel, in general, algoritmul pentru selectia vectorului de comutatie al tensiunii se realizeaza de asemenea in etape (etapele 1 - 8), conform celui prezentat anterior pentru regimul stationar. Totusi, daca in etapa a 8 - a nu mai exista o solutie pozitiva, de exemplu tk + tk + 1 ≤ Ts nu poate fi satisfacuta, atunci se presupune - mai intai - ca exista o schimbare a referintei cuplului electromagnetic. Astfel, se foloseste tabelul 5.3 pentru selectia celor doua stari potrivite de comutatie si se rezolva ecuatiile (5.45) si (5.46) pentru a determina tk si tk + 1. Daca rezulta o solutie pozitiva, atunci se aplica vectorii uk si uk + 1 pentru durata tk, respectiv tk + 1. Daca nu exista o solutie pozitiva atunci se presupune ca este prezenta o schimbare a fluxului statoric si prin urmare se rezolva ecuatiile (5.46) si (5.47). Daca exista solutii pozitive atunci se aplica vectorii de comutatie potriviti din tabelul 5.4 pe duratele tk respectiv tk + 1. Totusi, daca nu exista o solutie se aplica vectorii din tabelul 5.5 (starile de comutatie corespunzatoare si timpii de comutatie sunt iesirile spre invertor). Algoritmul predictiv se poate implementa cu un DSP, dar ar trebui considerat ca aceasta este o schema foarte intensa de calcul si la frecvente inalte de comutatie se pretind calcule foarte rapide.
Ar trebui notat ca, similar cu alte tipuri de scheme predictive, cand se foloseste schema predictiva prezentata, survine eroarea stationara a unei singure perioade Ts. Aceasta se datoreaza faptului ca estimarea cuplului electromagnetic si a fluxului statoric se bazeaza pe intrarile din perioada precedenta. O intarziere de o singura perioada este necesara pentru a estima semnalele de comutatie. Un regulator deadbeat ideal ar necesita estimari care sa fie executate in timp zero. Mai mult, regulatorul predicitiv se bazeaza numai pe erorile cuplului electromagnetic si fluxului statoric. Combinarea acestui fapt cu intarzierea de o perioada are drept rezultat o eroare stationara a cuplului electromagnetic. Totusi, a-ceasta nu prezinta nici o problema daca se utilizeaza si un regulator de viteza.
 O tehnica alternativa de
alegere predictiva a vectorului de comutatie, care nu necesita
calcule atat de intense ca aceea descrisa mai sus, se va discuta pe scurt
in continuare. Se presupune ca exista numai o schimbare a cuplului. Desi aceasta tehnica
alternativa nu are drept rezultat reglarea deadbeat a fluxului statoric,
va rezulta numai o degradare minima a performantei. Aceasta
tehnica alternativa se bazeaza pe limitarea marimii
tensiunii statorice de referinta (impuse) la valoarea instantanee
maxima permisa cu modulatia vectorului spatial, cum se
arata in fig. 5.8.
O tehnica alternativa de
alegere predictiva a vectorului de comutatie, care nu necesita
calcule atat de intense ca aceea descrisa mai sus, se va discuta pe scurt
in continuare. Se presupune ca exista numai o schimbare a cuplului. Desi aceasta tehnica
alternativa nu are drept rezultat reglarea deadbeat a fluxului statoric,
va rezulta numai o degradare minima a performantei. Aceasta
tehnica alternativa se bazeaza pe limitarea marimii
tensiunii statorice de referinta (impuse) la valoarea instantanee
maxima permisa cu modulatia vectorului spatial, cum se
arata in fig. 5.8.
In fig. 5.8 se
arata ca de fiecare data fazorul tensiunii de
referinta (us*), rezultat dintr-un
algoritm de reglare deadbeat, este in afara hexagonului tensiunii si
ca marimea tensiunii de intrare in modulatorul fazorului spatial
se limiteaza la tensiunea maxima a invertorului (![]() ). Tensiunea
). Tensiunea ![]() are acelasi unghi
are acelasi unghi
![]() ca si tensiunea
de referinta originara. Astfel, marimea vectorului de
referinta a tensiunii este data ca:
ca si tensiunea
de referinta originara. Astfel, marimea vectorului de
referinta a tensiunii este data ca:
 (5.48)
(5.48)
si unghiul este
schimbat fata de cel calculat folosind algoritmul dat mai sus. In
fig. 5.8 valoarea medie a tensiunii statorice pe o perioada de
esantionare (Ts) calculata cu schema predictiva
originara (nu cu cea alternativa) este ![]() ; aceasta este indicata prin vectorul cu linie
intrerupta. Varful acestui vector este la intersectia limitei
hexagonale a tensiunii de iesire cu fluxul statoric de
referinta. Totusi, cand se foloseste schema predictiva
echivalenta, tensiunea medie (
; aceasta este indicata prin vectorul cu linie
intrerupta. Varful acestui vector este la intersectia limitei
hexagonale a tensiunii de iesire cu fluxul statoric de
referinta. Totusi, cand se foloseste schema predictiva
echivalenta, tensiunea medie (![]() ) pe aceeasi perioada (Ts) se afla
pe limita tensiunii de acelasi unghi ca
) pe aceeasi perioada (Ts) se afla
pe limita tensiunii de acelasi unghi ca ![]() . Trebuie notat ca eroarea fluxului creste cu
cresterea marimii lui
. Trebuie notat ca eroarea fluxului creste cu
cresterea marimii lui![]() . Este interesant de observat ca
. Este interesant de observat ca ![]() este
dafazata inaintea lui
este
dafazata inaintea lui ![]() , cand cuplul electromagnetic trebuie sa fie crescut
si este defazat in urma lui
, cand cuplul electromagnetic trebuie sa fie crescut
si este defazat in urma lui ![]() cand cuplul
electromagnetic trebuie sa fie scazut. Urmeaza ca curentul
care produce cuplul este mai mare cu schema alternativa decat cu schema
predictiva originara. Aceasta conduce la performanta
dinamica imbunatatita, in ciuda faptului ca
schema alternativa nu prevede reglarea deadbeat a marimii fluxului.
Aceasta schema predictiva echivalenta poate fi de asemenea
folosita cand survine supramodulatia (adica in regiunea dintre
PWM continuu si functionare in sase pasi). Aceasta
regiune de functionare este un caz particular al schimbarii
cuplului/fluxului. Similar cu cele discutate mai sus, in regiunea de
tranzitie, vectorul de referinta
cand cuplul
electromagnetic trebuie sa fie scazut. Urmeaza ca curentul
care produce cuplul este mai mare cu schema alternativa decat cu schema
predictiva originara. Aceasta conduce la performanta
dinamica imbunatatita, in ciuda faptului ca
schema alternativa nu prevede reglarea deadbeat a marimii fluxului.
Aceasta schema predictiva echivalenta poate fi de asemenea
folosita cand survine supramodulatia (adica in regiunea dintre
PWM continuu si functionare in sase pasi). Aceasta
regiune de functionare este un caz particular al schimbarii
cuplului/fluxului. Similar cu cele discutate mai sus, in regiunea de
tranzitie, vectorul de referinta ![]() este situat in afara
limitei hexagonale. La limita, cum
este situat in afara
limitei hexagonale. La limita, cum ![]() devine mare in valoare
absoluta, tensiunea invertorului
devine mare in valoare
absoluta, tensiunea invertorului ![]() 'sare'
dintr-un colt al hexagonului in urmatorul, ceea ce este echivalent cu
functionarea in sase pasi.
'sare'
dintr-un colt al hexagonului in urmatorul, ceea ce este echivalent cu
functionarea in sase pasi.
4 Schema de reglare directa a cuplului motorului asincron folosind un invertor sursa de tensiune (VSI)
In figura 5.9 se arata schematic o forma simpla de actionare cu motor asincron cu controlul direct al cuplului folosind un invertor sursa de tensiune. In aceasta schema fluxul reglat este fluxul statoric, astfel ca ea se va denumi ca o actionare cu motor asincron cu reglare directa a cuplului bazata pe fluxul statoric.

Un
invertor sursa de tensiune (VSI) cu sase pulsuri alimenteaza
motorul asincron (MA). Asa cum s-a discutat anterior, controlul direct al
cuplului implica controlul separat al fluxului statoric si al
cuplului prin alegerea optima a modurilor de comutatie a
invertorului. Tabelul de comutatie optima (tab. 5.1) a fost
aratat in paragraful 2. In fig. 5.9 valoarea impusa (de
referinta) a fluxului statoric ![]() se compara cu
valoarea reala s si eroarea rezultata
alimenteaza un comparator de flux cu histerezis cu doua nivele.
Similar, valoarea de referinta a cuplului electromagnetic (
se compara cu
valoarea reala s si eroarea rezultata
alimenteaza un comparator de flux cu histerezis cu doua nivele.
Similar, valoarea de referinta a cuplului electromagnetic (![]() ) se compara cu valoarea reala (me)
si semnalul de eroare a cuplului electromagnetic alimenteaza un
comparator de cuplu cu histerezis cu trei nivele. Iesirile comparatoarelor
de flux si cuplu se utilizeaza in tabelul de comutatie
optima (tabelul de cautare), care de asemenea foloseste
informatia de pozitie a fazorului spatial al fluxului. In figura 5.9 erorile de flux si cuplu
electromagnetic se limiteaza in interiorul benzilor de histerezis, care
sunt de latime 2.s si respectiv 2.me.
Banda de histerezis de flux influenteaza in special distorsiunea
curentului statoric pe baza armonicilor de ordin redus iar banda de histerezis
de cuplu influenteaza frecventa de comutatie si astfel
pierderile de comutatie. Schema de reglare directa a cuplului
necesita estimarile fluxului si cuplului electromagnetic.
) se compara cu valoarea reala (me)
si semnalul de eroare a cuplului electromagnetic alimenteaza un
comparator de cuplu cu histerezis cu trei nivele. Iesirile comparatoarelor
de flux si cuplu se utilizeaza in tabelul de comutatie
optima (tabelul de cautare), care de asemenea foloseste
informatia de pozitie a fazorului spatial al fluxului. In figura 5.9 erorile de flux si cuplu
electromagnetic se limiteaza in interiorul benzilor de histerezis, care
sunt de latime 2.s si respectiv 2.me.
Banda de histerezis de flux influenteaza in special distorsiunea
curentului statoric pe baza armonicilor de ordin redus iar banda de histerezis
de cuplu influenteaza frecventa de comutatie si astfel
pierderile de comutatie. Schema de reglare directa a cuplului
necesita estimarile fluxului si cuplului electromagnetic.
Cum s-a discutat in 3.2 componentele fluxului statoric se pot obtine prin integrarea tensiunilor monitorizate corespunzatoare mai putin caderile de tensiune ohmice, cum se arata in ecuatiile (5.42) si (5.43), dar la frecvente joase se pot produce erori mari datorita variatiei rezistentei statorice, derivei de integrare si a zgomotului. Cuplul electromagnetic se poate estima folosind ecuatia (5.1); astfel
![]() (5.49)
(5.49)
Reglarea vitezei se poate obtine folosind un regulator de viteza (de exemplu un regulator PI sau un regulator fuzzy logic etc.), a carui iesire va da cuplul impus (de referinta) iar intrarea regulatorului de viteza va fi diferenta dintre viteza impusa si viteza reala.
5 Reducerea ondulatilor fluxului statoric si cuplului electromagnetic
In actionarea cu motor asincron si reglarea directa a cuplului exista ondulatii ale cuplului si fluxului, deoarece nici unul dintre vectorii de comutatie ai invertorului nu este capabil - in cele mai multe cazuri de comutatie - sa genereze exact tensiunea statorica necesara pentru a produce schimbarile dorite ale cuplului electromagnetic si ale fluxului statoric. Totusi, ondulatiile cuplului electromagnetic si ale fluxului statoric se pot reduce utilizand diferite tehnici, dintre care unele implica folosirea frecventelor ridicate de comutatie sau schimbarea topologiei invertorului, dar este de asemenea posibil sa folosim scheme care nu implica frecvente ridicate de comutatie sau schimbarea topologiei invertorului, ca de exemplu reglarea factorului de umplere [21].
In actionarea cu motor asincron si controlul direct al cuplului, frecventa de comutatie crescuta este dorita deoarece reduce continutul armonic al curentilor statorici si de asemenea conduce la armonici de cuplu reduse. Totusi, daca se foloseste o frecventa ridicata de comutatie, aceasta va provoca o crestere importanta a pierderilor de comutatie (conducand la reducerea randamentului) si o crestere a solicitarilor elementelor semiconductoare ale invertorului. Aceasta este motivul pentru care invertoarele de mare putere (de exemplu in tractiunea Diesel - electrica) functioneaza la frecvente reduse de comutatie, de cateva sute de Hz. In cazul frecventelor ridicate de comutatie, este necesar un procesor rapid, deoarece timpul de procesare se reduce. Aceasta insa creste costurile. In actionarea ABB cu controlul direct al cuplului (a se vedea 5.4) se foloseste un procesor digital de semnal de mare viteza de 40 MHz [cu un circuit integrat cu aplicatie specifica (ASIC) hard] pentru a determina frecventa de comutatie a invertorului [21]. Daca se utilizeaza topologia schimbata a invertorului, este posibil sa se foloseasca un numar crescut de comutatii, dar aceasta va creste de asemenea costul. Se poate creste numarul starilor de comutatii prin utilizarea a doua invertoare, cu GTO, conectate in paralel. Desi in acest sistem se creste numarul starilor de comutatie diferite de zero la 18, se produc curenti de secventa zero. In actionarea traditionala cu motor asincron si reglarea directa a cuplului (dsicutata inainte) se aplica un vector de tensiune pentru intreaga perioada de comutatie si aceasta produce cresterea curentului statoric si a cuplului electromagnetic pe intreaga perioada de comutatie. Astfel pentru erori mici, cuplul electromagnetic depaseste valoarea sa impusa mai devreme in timpul ciclului si continua sa creasca, producand o ondulatie mare a cuplului. Aceasta este apoi urmata de ciclul de comutatie in care se aplica vectori de comutatie zero pentru a reduce cuplul electromagnetic la valoarea sa impusa. Se poate obtine o solutie prin care ondulatiile cuplului si fluxului se pot reduce prin folosirea vectorului selectionat de comutatie numai pentru o parte a perioadei de comutatie (care este definita ca factor de umplere, δ) si folosirea vectorului zero pentru restul perioadei. Timpul de aplicare a vectorului activ (diferit de zero) se alege astfel incat sa creasca cuplul electromagnetic spre valoarea sa de referinta. Cand cuplul electromagnetic atinge valoarea sa de referinta se aplica vectorul zero. In timpul aplicarii vectorului zero, se aplica masinii tensiunea zero si astfel cuplul electromagnetic este aproape constant; el descreste usor. Valoarea medie a tensiunii de alimentare a motorului asincron in timpul aplicarii fiecarui vector de comutatie este δE (E este tensiunea continua din circuitul intermediar de c.c.). Prin variatia factorului de umplere intre 0 si 1, este posibil sa se aplice, in timpul fiecarei perioade de comutatie, orice tensiune intre 0 si E. Aceasta creste alegerea vectorului de tensiune care - intr-un DTC conventional - este limitat la numarul vectorilor de comutatie. Cum s-a stabilit mai sus, factorul de umplere se alege astfel incat sa dea un vector de tensiune a carui valoare medie pe un ciclu de comutatie [21] sa dea schimbarea dorita a cuplului, avand drept rezultat ondulatii reduse ale cuplului.
 Factorul de
umplere al fiecarei stari de comutatie este o functie
neliniara a erorii cuplului electromagnetic si a erorii fluxului
statoric si de asemenea o functie de pozitia fazorului
spatial al fluxului statoric. Astfel este dificil de modelat aceasta
functie neliniara. Totusi, prin folosirea unui sistem de control
direct al cuplului bazat pe logica fuzzy este posibil sa se realizeze
reglarea factorului de umplere in timpul fiecarui ciclu de comutatie.
Intr-un asemenea sistem exista doua intrari, eroarea cuplului
electromagnetic eme = me - me
si pozitia fluxului statoric s. Iesirea
regulatorului cu logica fuzzy este factorul de umplere δ (fig. 5.10).
Factorul de
umplere al fiecarei stari de comutatie este o functie
neliniara a erorii cuplului electromagnetic si a erorii fluxului
statoric si de asemenea o functie de pozitia fazorului
spatial al fluxului statoric. Astfel este dificil de modelat aceasta
functie neliniara. Totusi, prin folosirea unui sistem de control
direct al cuplului bazat pe logica fuzzy este posibil sa se realizeze
reglarea factorului de umplere in timpul fiecarui ciclu de comutatie.
Intr-un asemenea sistem exista doua intrari, eroarea cuplului
electromagnetic eme = me - me
si pozitia fluxului statoric s. Iesirea
regulatorului cu logica fuzzy este factorul de umplere δ (fig. 5.10).
|
Politica de confidentialitate |
| Copyright ©
2024 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |