
Transformari de axe ale sistemului bifazat
Schimbarea de axe ale unui fazor spatial, descompus in componente dupa axa reala si imaginara, conduce la trasnformari de axe in sistemul bifazat de marimi. Este indicat ca aceasta transformare sa se faca matriceal.
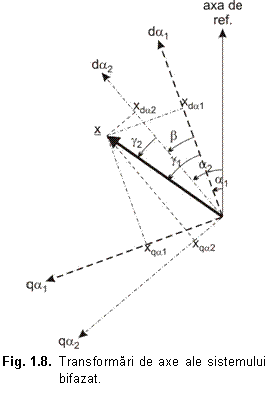
Consideram axele d si q ale sistemului bifazat suprapuse peste axele reale respectiv imaginare ale planului complex corespunzator.
Proiectam fazorul spatial (fig. 1.8) mai intai pe directiile d1, q1. Obtinem astfel fazorul spatial x scris in planul 1 astfel:
![]() . (1.38)
. (1.38)
Acelasi fazor raportat la planul complex 2 va avea expresia:
![]() . (1.39)
. (1.39)
Expresiile (1.38) si (1.39) pot fi scrise matriceal conform relatiei (1.20) astfel:
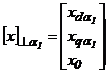 si
si  . (1.40)
. (1.40)
Componenta homopolara x0 a sistemului trifazat este o marime scalara - rel. 1.15 - si nu depinde de sistemul de axe (nu se reprezinta in planul complex).
 Schimbarea sistemului de axe este
echivalenta cu schimbarea de variabila; se trece deci de la
Schimbarea sistemului de axe este
echivalenta cu schimbarea de variabila; se trece deci de la ![]() la
la ![]() . Din fig. 1.8, prin relatii geometrice, se obtin
compo-nentele bifazate astfel:
. Din fig. 1.8, prin relatii geometrice, se obtin
compo-nentele bifazate astfel:
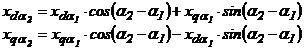 .
.
Deoarece componenta homopolara se pastreaza prin schimbarea sistemului de axe, pe baza relatiilor de mai sus se poate scrie relatia de recurenta sub forma matriceala:
![]() . (1.41)
. (1.41)
Notand
![]() :
:
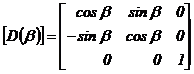 . (1.42)
. (1.42)
Trecand de la sistemul de axe 1 la 2, unghiul al matricei de transformare (1.42) se va masura de la axa reala a sistemului 1 spre axa reala a sistemului 2.
Pentru transformarea inversa de la 2 la 1, unghiul al matricei [D()] va fi acelasi dar cu semn schimbat. In acest caz:
![]() .
.
Se obtine deci:
![]() . (1.43)
. (1.43)
Matematic, expresia (1.43) se obtine din relatia (1.41), inmultind la stanga cu inversa matricii [D]:
![]() ,
,
![]() . (1.44)
. (1.44)
Din relatiile (1.43) si (1.44) se observa urmatoarea proprietate a matricei de transformare:
![]() , (1.45)
, (1.45)
unde
![]() este matricea
transpusa a lui
este matricea
transpusa a lui ![]() .
.
In cazul unei schimbari de variabile succesive, matricea de transformare se aplica de doua ori succesiv, adica:
![]() . (1.46)
. (1.46)
Se vede ca diferentele de unghiuri 1 si 2 se aduna. Daca, de exemplu, 1 = 2 - 1 si 2 = 3 - 2 trecerea de la sistemul 1 la sistemul 3 se face cu matricea [D(3)] = [D(1 + 2)] = [D(3 - 1)] in care 3 este 3 - 1.
Matricea D[()] este un operator de rotire cu unghiul al sistemului de axe la care se raporteaza fazorul spatial, adica la care se proiecteaza fazorul spatial pentru a obtine componentele d - q
Conform
expresiilor (1.40) componenta homopolara a unei matrice in sistemul
bifazat ![]() nu este o componenta a fazorului spatial aferent.
nu este o componenta a fazorului spatial aferent.
Daca
se defineste scrierea restransa a matricei ![]() , continand numai componentele d - q ale fazorului
spatial, adica:
, continand numai componentele d - q ale fazorului
spatial, adica:
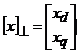 , (1.47)
, (1.47)
atunci operatorul de rotire prezinta proprietatea:
![]() , (1.48)
, (1.48)
unde:
![]() . (1.49)
. (1.49)
Relatia (1.48) exprima proprietatea unui vector a carui derivata are o componenta rotita inainte cu 900.
|
Politica de confidentialitate |
| Copyright ©
2024 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |