
Constructia si calculul arborelui cotit
Arborele cotit transforma, cu ajutorul bielei, miscarea de translatie in miscare proprie de rotatie si transmite spre utilizare momentul motor dezvoltat de forta de presiune a gazelor. La motoarele policilindrice arborele cotit insumeaza lucrul mecanic produs de fiecare cilindru si il transmite utilizatorului. De asemenea arborele cotit antreneaza in miscare unele sisteme auxiliare ale motorului cum ar fi: mecanismul de distributie, pompa de injectie, pompa de lichid, alternatorul, ventilatorul, etc.
Elementele componente ale arborelui cotit sunt: capatul liber; fusurile paliere; fusurile manetoane; bratele; contragreutatile; partea posterioara de care se fixeaza volantul.
In majoritatea cazurilor pe capatul liber al arborelui cotit se amplaseaza elemente de etansare pentru ulei cum ar fi deflectorul si garnitura de etansare, pinionul pentru actionarea distributiei, fulia pentru ventilator, clichetul (racul) pentru pornire manuala. Pentru montarea acestor organe capatul liber se executa in trepte. Uneori pe capatul din fata al arborelui se monteaza amortizoare de vibratii torsionale. Acestea pot fi cu frecare uscata sau lichida.
Fusurile paliere sunt fusurile ce se gasesc pe axa de rotatie a arborelui cotit si prin intermediul carora se sprijina in lagarele executate in carterul superior al motorului.
Fusurile manetoane sunt fusurile ce se gasesc de-a lungul si in jurul axei de rotatie a arborelui cotit la distanta r = S/2 fata de acesta, servind pentru articularea bielelor.
Bratele sunt partile arborelui cotit ce realizeaza legaturile dintre cele doua tipuri de fusuri si pot avea diferite forme constructive.
Contragreutatile sunt mase dispuse pe prelungirea bratelor, in sens opus fusului maneton, cu scopul de a ameliora echilibrajul fortelor de inertie si al momentelor lor si a descarca partial lagarele.
Partea posterioara sau capatul din spate se executa cu o flansa pentru montarea volantului. Fixarea volantului se face cu suruburi care trebuie sa asigure prin strangere, pe suprafata imbinarii dintre flanse si volant, un moment de frecare mai mare decat momentul motor. Etansarea capatului din spate se obtine prin combinarea inelelor deflectoare cu garnituri inelare din plasa sau cauciuc si prin efect de labirint creat printr-o portiune filetata a arborelui cotit, filetul fiind practicat in sens invers sensului de rotatie al acestuia.
Asadar, in principal, arborele cotit este compus dintr-un numar de coturi ce depinde de numarul si dispunerea cilindrilor, coturi ce sunt amplasate de-a lungul si in jurul axei de rotatie. Dispunerea lor este conditionata de o buna echilibrare naturala a motorului policilindric, precum si asigurarea unei uniformitati a aprinderilor pe ciclu care la randul ei determina o uniformitate a momentului motor total. In cea mai simpla alcatuire orice cot al arborelui cuprinde un fus maneton si doua brate incadrate de doua fusuri paliere.
La motoarele cu cilindri in linie, arborele are cate un cot pentru fiecare cilindru. Solutia clasica se obtine cand numarul de fusuri paliere este I+1 ( I numarul de cilindri). Ea asigura incarcari moderate ale elementelor arborelui, masa si uzura lui fiind corespunzator limitate. Pentru unele MAS-uri de automobil, arborele cotit se construieste cu un numar mai mic de fusuri paliere, daca fortele preluate sunt reduse, datorita nivelului coborat al presiunii maxime a gazelor. Se realizeaza in acest fel un motor compact (arbore scurt), dar se majoreaza solicitarea arborelui cotit la incovoiere, ca rezultat a cresterii distantelor dintre reazeme. De aceea este necesara sporirea rigiditatii arborelui, ceea ce se realizeaza prin cresterea diametrului fusurilor si scaderea lungimilor, precum si prin marirea dimensiunilor bratelor. In consecinta, exista in prezent tendinta de revenire la solutia cu I+1 fusuri paliere, pentru motoare rapide si cu cilindree ridicate.
La motoarele cu cilindri in V numarul de coturi este egal cu I/2, iar fusurile paliere alterneaza cu fusurile manetoane.
Fortele preluate de arborele cotit, periodic variabile, produc momente incovoietoare si de torsiune, de asemenea variabile periodic, care solicita elementele arborelui cotit la oboseala. Aceasta solicitare este indeosebi periculoasa in zonele unde rezistenta la oboseala e micsorata organic, prin concentrari importante ale eforturilor unitare: la trecerile dintre fusuri si brate, caracterizate prin variatii bruste de sectiune si in dreptul orificiilor care sunt prevazute fusurile pentru vehicularea uleiului de ungere. Solicitarile arborelui au si caracter de soc, datorita jocurilor din articulatii, vitezei mari de crestere a presiunii in timpul arderii si schimbarilor de sens ale fortelor aplicate. Suplimentar fusurile arborelui sunt supuse frecarii si uzurii. Din cauza solicitarilor de incovoiere, arborele cotit se deformeaza astfel incat compromite coaxialitatea fusurilor si cuzinetilor, ceea ce determina uzura lagarelor. In plus o rigiditate insuficienta a carterului ca si a bratului insusi provoaca ruperea cotului.
Momentele care solicita arborele cotit genereaza vibratii de incovoiere si torsiune ale acestuia. Vibratiile de incovoiere se asociaza cu vibratiile axiale intrucat deformatiile radiale ale cotului provoaca deplasari axiale intrucat deformatiile radiale ale cotului provoaca deplasari axiale ale fusurilor paliere. Deoarece amplitudinile vibratiilor de incovoiere sunt limitate datorita montarii fusurilor in lagare, aceste vibratii devin periculoase numai daca jocurile din lagare se maresc exagerat. Mult mai importante pot fi implicatiile vibratiilor de torsiune, deoarece deformatiile unghiulare ale arborelui nu sunt controlate decat de rigiditatea lui. La rezonanta, cand una din frecventele proprii ale arborelui, egaleaza o frecventa a excitatiei, amplitudinile vibratiei cresc considerabil ceea ce poate produce adesea ruperi caracteristice dupa o diagonala, in deosebi la ultimul fus palier precum si uzuri suplimentare ale fusurilor si cuzinetilor.
Se observa asadar ca dintre toate organele motorului arborele cotit suporta cele mai mari solicitari. De aceea nivelul si varietatea solicitarilor impun ca arborele cotit sa prezinte valori inalte ale rezistentei la oboseala, rigiditatii si rezistentei la uzura a fusurilor, precum si susceptibilitatea redusa la rezonanta a vibratilor de torsiune. De o deosebita importanta pentru controlul deformatiilor este realizarea unei rigiditati ridicate care implica insa o masa mare a arborelui, ceea ce se reflecta prin supradimensionarea elementelor lui. Dimensionarea prea larga nu este recomandabila pentru a preveni cresterea exagerata a masei motorului, din care masa arborelui cotit reprezinta 8,5 14 %; in plus, limitand masa arborelui cotit se evita fortele de inertie excesive si turatiile critice de rezonanta coborate.
Calitatile cerute arborelui cotit se asigura prin utilizarea unui material superior si prin forma constructiva si executii adecvate.
2. Constructia arborelui cotit
Arborele cotit este de doua feluri: demontabil si nedemontabil; ultima solutie se utilizeaza pe scara larga.
Fusurile arborelui cotit se construiesc astfel incat suprafata portanta sa fie cat mai mare. Diametrele fusurilor cu acelasi rol sunt esentiale, dp la fusurile paliere si dm la fusurile manetoane. Se prefera de obicei ca dm<dp. Lungimile fusurilor paliere depind de incarcarea fiecaruia. Adesea fusul palier din mijlocul arborelui cotit este mai lung decat celelalte determinat de fortele care incarca fusul si articulatiile constructive care permit dispunerea in lungul acestui fus a unor elemente de fixare axiala a arborelui cotit. Fusurile manetoane au aceiasi lungime lm datorita identitatii bielelor prinse direct pe ele. Scurtarea excesiva a fusului maneton este optionala, intrucat antreneaza importante scapari laterale de ulei, impunand supradimensionarea pompei de ulei. Lungimea lm este marita de aproape doua ori la motoarele in V cu biele alaturate.
O constructie mai simpla se obtine daca fusurile arborelui cotit nu au canale axiale. Pentru a micsora masa arborelui cotit si fortele de inertie se recurge deseori la gaurirea axiala a fusurilor. Solutia este convenabila si din punct de vedere al rezistentei la oboseala deoarece asigura o distributie favorabila a fluxului de forte. La fusul maneton este avantajoasa deplasarea gaurii in raport cu axa acestuia; datorita excentricitatii efectul de concentrare al eforturilor unitare la trecerea spre brat este atenuat mai mult, iar rezistenta la oboseala creste cu 1015%; de asemenea se micsoreaza forta de inertie a cotului si deci incarcarea lagarelor. Pentru a executa canalul ce transmite uleiul de la fusul palier la fusul maneton, este uneori necesara si excentricitatea laterala.
Bratele arborelui cotit au forma dreptunghiulara la unele motoare lente, ceea ce asigura simplitatea constructiei. Mai rationala sub aspectul reducerii masei arborelui si a costului de fabricatie sunt formele obtinute prin indepartarea materialului din zonele care nu participa la transmiterea eforturilor. Pentru a mari lungimile fusurilor (reducerea uzurii), in cazul distantei fixate intre doua coturi consecutive se micsoreaza grosimea bratelor, realizand sectiunea necesara prin marirea latimii. Se obtin astfel brate de forma ovala sau circulara. Arborii cotiti cu asemenea brate se utilizeaza frecvent la motoare rapide, de puteri mari. Executia lor este mai costisitoare dar antreneaza reducerea importanta a masei cresterea rezistentei si a rigiditatii. In aceste privinte cea mai avantajoasa este forma ovala ce asigura o foarte buna comportare la oboseala. O cerinta deosebita consta in eliminarea efectului de concentrare a eforturilor la trecerile fus-brat. In acest scop, fusurile se racordeaza cu bratele sau cu praguri intermediare; intrucat racordarea se rectifica simultan cu fusul, pragul previne contactul pietrei de rectificat cu bratul.
Efecienta solutiei se apreciaza in functie de marimea suprapunerii determinata de-a lungul axei de simetrie a bratului.
Contragreutatile ce echipeaza arborele cotit determina marirea masei lui si deci a masei motorului; cresterea masei motorului este mai putin insemnata, deoarece utilizarea contragreutatilor permite reducerea dimensiunilor volantului, la acelasi grad de neregularitate. Aportul de masa datorat contragreutatilor micsoreaza frecventele proprii ale arborelui cotit favorizand rezonanta. Contragreutatile introduc si importante dificultati de fabricatie. Aceste impedimente, indeosebi executia mai dificila, impun anumite rezerve in folosirea contragreutatilor. Adesea, arborele cotit nu are contragreutati daca cerintele privind echilibrajul si descarcarea lagarelor sunt indeplinite intr-o masura satisfacatoare pe alte cai: cand se realizeaza un echilibraj avansat in dispunerea relativa a coturilor si distante scurte intre lagare, ca in cazul arborelui cotit ce are plan central de simetrie si fusuri palier alternand cu fusurile manetoane; cand motorul este dotat cu un bloc-carter, ceea ce confera rigiditate sporita lagarelor. Se prevad in schimb contragreutati la arbori cu numar redus de fusuri paliere.
Sub aspectul descarcarii lagarelor, se recomanda utilizarea contragreutatilor pentru a limita produsul dintre presiunea medie pe fusul palier si viteza sa periferica, ce exprima in prima instanta rezistenta lagarului la uzura.
Pentru obtinerea unei mase cat mai mici, contragreutatile trebuie astfel construite incat sa aiba centrul de masa cat mai departe de axa de rotatie a arborelui cotit. Dimensiunile in directia radiala sunt limitate de spatiul disponibil fata de carter, cilindru si pistonul aflat la p.m.e. Respectand aceste conditii, contragreutatile au frecvent forma unui sector de cerc sau a unui segment de cerc. Grosimea lor poate depasi grosimea bratelor, daca nu afecteaza spatiul necesar miscarii bielei. Prin contragreutati se echilibreaza de regula 60-70% din forta de inertie a maselor cu miscare de rotatie aferente unui cot.
In unele cazuri (motoare mici) contragreutatile fac corp comun cu bratele ceea ce este posibil datorita dimensiunilor mai reduse. Apar insa dificultati de realizare a formelor celor mai potrivite, mai ales cand semifabricatul este obtinut prin deformare la cald.
Se recomanda si chiar este obligatorie in cazul arborilor cotiti mari, este executia contragreutatilor detasabile, construite in general din fonta. De obicei ele se fixeaza cu suruburi. Imbinarea trebuie sa evite solicitarea dezavantajoasa a suruburilor. Daca se practica prinderea prin coada de randunica suruburile sunt incarcate numai de forta de strangere. La alte solutii suruburile sunt solicitate si de forta centrifuga a greutatii si descarcate de forta de inertie tangentiala prin praguri, danturi triunghiulare, sau bucse de centrare. Uneori suruburile nu sunt asigurate ci stranse cu un moment care situeaza deformatia in domeniul elastic.
La o solutie moderna contragreutatile sunt prevazute cu orificii in care se preseaza sau se monteaza prin filet role. Deplasarea axiala a rolelor este impiedicata prin stemuirea marginilor orificiilor. Rolele se fabrica dintr-un material greu numit triamet obtinut prin sintetizare pe baza de wolfram si liant de Ni-Cu.
Pentru ungerea fusurilor, in arborele cotit se prevad canale de vehiculare a uleiului. De regula, uleiul este adus la periferia fiecarui fus palier prin canale practicate in carter, din rampa centrala de ungere; patrunzand prin orificiile executate in fusurile paliere uleiul este transmis spre fusurile maneton, traseele traversand bratele. Este necesar sa se dispuna canalele din brate cat mai departe de zonele periculoase de la racorduri. Cand se prevad gauri longitudinale in fusuri, se evita intersectia lor de catre canalele din brate sau se adopta alte masuri. Astfel uleiul este uneori dirijat prin conducte incorporate la turnare in arbore. Alteori se obtureaza canalul longitudinal al fusului palier, de exemplu cu capace presate, si se executa canal de intrare; fusul maneton nu se inchide la capete, pentru a limita forta centrifuga.
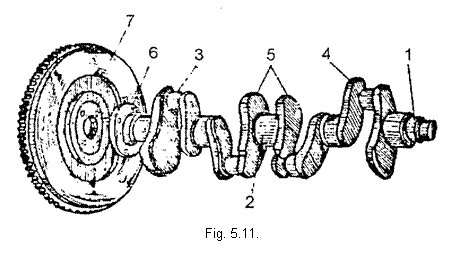
1 - capatul liber al arborelui cotit; 5 - contragreutati
2 - fusuri paliere; 6 - partea posterioara
3 - fusuri manetoane; 7 - flansa
4 - brate;
3. Materiale pentru arbori cotiti
Materialul pentru arborele cotit depinde de procedeul de fabricatie si de dimensiunile arborelui. Arborele cotit se confectioneaza prin doua procedee prin forjare si prin turnare. Forjarea se executa liber sau in matrita, cand lungimea arborelui nu depaseste aproximativ 2 m. Forjarea la matrita prezinta avantajul ca fibrele, urmand conturul presei, nu comporta intrerupere. Arborii cotiti forjati se confectioneaza din otel, cei turnati se confectioneaza din fonta sau otel.
Pentru turnarea arborelui cotit se utilizeaza in deosebi fonta care s-a dovedit foarte avantajoasa. Fonta poseda proprietati de turnare mai bune decat otelul ceea ce simplifica fabricatia si are un pret de cost mai redus. Ea insa are o rezistenta mica la incovoiere, dar utilizarea ei este posibila atribuind fusurilor si bratelor dimensiuni mai mari si rezemand fiecare cot pe doua fusuri paliere, ceea ce este in concordanta cu tendinta moderna de rigidizare a arborelui cotit. Fonta este un material cu calitati antifictiune superioare, datorita incluziunilor de grafit, de aceea uzura fusurilor este inferioara. Datorita actiunii lubrefiante a grafitului, fonta suporta presiuni specifice mai mari, ceea ce face posibila utilizarea cuzinetilor din bronz cu plumb. De asemenea, este de remarcat capacitatea mai inalta a fontei de a amortiza vibratiile torsionale, determinata de aceleasi incluziuni de grafit.
Avand in vedere cele de mai sus am adoptat pentru solutia aleasa un arbore cotit din fonta cu grafit nodular avand limita de curgere de 450 MPa, rezistenta la rupere de 700 MPa.
4. Calculul de rezistenta pentru solutia adoptata
a) Verificarea arborelui cotit la oboseala
Ipoteze de calcul:
- se considera fiecare cot izolat de restul arborelui cotit ca fiind un sistem de bare simplu rezemat pe lagarele paliere corespunzatoare;
- reazemele sunt rigide si coaxiale;
- in reazemul din stanga cotului se considera ca actioneaza un moment de torsiune Ns care reprezinta suma momentelor de torsiune a coturilor care preced cotul considerat , iar in reazemul din dreapta actioneaza un moment de torsiune care este dat de suma dintre momentul Ns si momentul de torsiune al cotului considerat;
- se inlocuieste sarcina distribuita transmisa de biela cu o forta concentrata S care actioneaza pe directia axei bielei. Aceasta forta se descompune in doua componente, o componenta Z ce actioneaza in planul sistemului de bare si o componenta T perpendiculara pe acest plan; pe suportul componentei Z actioneaza forta de inertie a manetonului Frm si forta de inertie a masei m a bielei aferenta manetonului Frb;
- lagarele paliere se inlocuiesc cu reazeme simple care actioneaza la jumatatea lor si preiau forte atat in planul cotului cat si in plan perpendicular pe acesta;
se iau in considerare fortele de inertie ale bratelor Frbr si ale contragreutatilor Frcg
1. Stabilirea sarcinilor care actioneaza asupra cotului si determinarea reactiunilor
Se calculeaza:
- fortele de inertie ale maselor neechilibrate ale celor doua brate
Frbr = mbr rbr w (5.93)
unde
- mbr este masa neechilibrata a unui brat;
- rbr raza cercurilor pe care se deplaseaza centrele de masa ale bratelor cotului;
w viteza unghiulara a arborelui cotit
- fortele de inertie ale maselor contragreutatilor; se considera cazul in care pe prelungirea fiecarui brat se gaseste cate o contragreutate. Ele sunt definite de relatia:
Frcg = mcg rcg w (5.94)
unde :
- mcg este masa unei contragreutati;
- rcg raza cercurilor pe care se deplaseaza centrele de masa ale contragreutatilor.
- forta de inertie a masei manetonului Frm definita de relatia:
Frm = mmrm w (5.95)
unde:
-mm = pdm2/4 lm d, dm = 44mm diametrul manetonului, lm = 23 mm lungimea manetonului, d densitatea fontei d = 7850 kg/m, deci mm = 4,19 kg.
- rm = r = 86,4 mm
Se calculeaza masa contragreutatii:
mcg = y(R12 - R22 ) h r (5.96)
in care:
y pentru arborii cotiti ai motoarelor de automobil este y = 70 = 1,22 rad;
- h = 0,2D =40,32 mm;
r densitatea fontei r = 7850 kg/m
- R1 = r + dm/2+5 = 136,8 mm;
- R2 = dp/2 + 7 = 64,6 mm.
Inlocuind valorile in relatia de mai sus rezulta: mcg = 0,52 kg
Raza rcg se calculeaza cu relatia:
rcg=2/3 siny y (R12 + R1R2 +R22 )/(R1+R2) (10.5)
in care R1, R2, y au valorile de mai sus, deci: rcg = 21 mm
Contragreutatile dispuse pe cele doua brate se calculeaza din conditia ca ele sa echilibreze numai o fractiune f =65% din forta totala de inertie a maselor in miscare de rotatie ce actioneaza asupra unui cot . Deci:
2Frg=f(Frb+Frm+2Frb) (5.97)
sau folosind relatiile lor de definitie:
mcg rcg=f/2(m2 r+mm r+2mbr rbr) (5.98)
in care:
- m2 = 3,29 kg;
- rbr = 38.56 mm;
Celelalte marimi fiind calculate mai sus se poate determina mbr = 0,48 kg.
Cunoscand marimile ce intervin in relatiile fortelor, acestea se pot determina:
FRbr = 12676 N ; FRcg = 7191 N ; FRM = 2467,8 N
Reactiunile se calculeaza cu ajutorul ecuatiilor de echilibru static ale solidului rigid. Luand in considerare numai sarcinile care actioneaza in planul cotului si acceptand ca fusurile paliere au aceeasi lungime se determina Zs si Zd cu relatia:
Zs=Zd= FRbr - FRcg + (FRbr+FRM)/2 - Z/2 = F - Z/2 (5.99)
in care:
- Z = Zmax = 159589,67 N ;
- FRbr = 12676 N
Din conditia de echilibru a momentelor fata de axa fusurilor paliere, rezulta:
Md = Ms+T r (5.100)
in care:
- Ms=0
- T = 19559 N deci, Md = 1682 N m
2. Ridicarea diagramelor de eforturi
Pentru ridicarea diagramei momentelor incovoietoare se dau expresiile momentelor in punctele caracteristice:
Mva = Mvb = 0
Mv1 = Mv5 = - Zs a; (5.101)
Mv2 = Mv4 = - Zs a;
Mv3 = - Zs l/2 - (Frcg - Frbr) (l/2 - a)
in care:
- Zs, Frcg, Frbr au fost calculate mai sus;
- l = lp+lm+2h, unde h = 0,22 d, deci l = 206,78 mm;
- a = (lp+h)/2 = 48,96 mm.
Inlocuind valorile in relatiile momentelor se obtine:
Mva = Mvb = 0; Mv1 = Mv5 = -55507 N m;
Mv2 = Mv4 = -55507 N m; Mv3=-88942,8 N m
Pentru trasarea diagramei momentelor incovoietoare in planul perpendicular pe planul cotului, expresiile momentelor in punctele caracteristice sunt:
Mha = Mhb = 0
pentru barele (A-1) si (B-5): pentru bara (1-2):
Mh1 = Mh5 = - T a/2 Mh1 =Ms
Mh2 = Ms - T r/2
pentru bara (2-4): pentru bara (4-5):
Mh2 = Mh4 = - T a/2 Mh4 = Ms - T r/2
Mh3 = - T l/4 Mh5 =Md =Ms - T r
in care valorile ce intra in relatiile momentelor au fost calculate mai sus, deci:
Mha = Mhb = 0; Mh1 = Mh5 = - 469,41 N m;
Mh1 = 0; Mh2 = Mh4 = -841 N m;
Mh2 = -841 N m; Mh3 = 1007,28 N m;
Mh4 = -841 N m; Mh5 = -1682 N m
Pentru trasarea diagramei momentelor de torsiune avem:
Ma = M1 = Ms
pentru barele (1-2) si (4-5):
M1 = M2 = M4 = M5 = - T r/2
pentru bara (2-4): pentru bara (B-5):
M2 = M4 = Ms - T r/2 Mb = M5 = Md = Ms - T r
Inlocuind valorile in relatiile de mai sus obtinem:
Ma = M1 = Ms = 0;
M1 = M2 = M4 = M5 = -469,41 N m;
M2 = M4 = -841 N m;
Mb = M5 = Md = -1682 N m
Pe baza rezultatelor de mai sus se pot trasa diagramele de eforturi.
b) Calculul la oboseala al fusului maneton
Fusul este solicitat la incovoiere in planul cotului si in planul perpendicular pe planul cotului, precum si la torsiune, eforturile maxime aflandu-se la mijlocul fusului. Deoarece tot aici se afla si orificiul de ungere, aceasta este sectiunea periculoasa unde se va dezvolta calculul in continuare. Variatia eforturilor in timpul rotatiei arborelui cotit impune luarea in considerare a fenomenului de oboseala a materialului. In concluzie fusul maneton se verifica la oboseala pentru un ciclu asimetric de incovoiere si torsiune.
Relatiile momentelor in sectiunile periculoase au expresiile:
Mv = - Zs l/2 - (Frcg - Frbr)(l/2 - a);
Mh = - T l/2; (5.102)
Mt = Ms - T r/2.
Desi in dreptul orificiului de ungere, pe suprafata exterioara a manetonului tensiunea s este mai mica, aici se considera punctul periculos datorita fenomenului de concentrare a tensiunii.
s = (-Mv cosj + Mh sinj)/Wi (5.103)
in care:
- Mv si Mh se determina cu relatiile de mai sus, pentru a
j unghiul de inclinare al orificiului de ungere j
Modulul de rezistenta la incovoiere (Wi) se calculeaza cu relatia:
Wi =![]() (5.104)
(5.104)
in care dm este diametrul exterior al manetonului.
Tensiunea tangentiala (t) se determina cu relatia:
t = Mt/Wp (5.105)
in care:
- Mt este momentul de torsiune care se calculeaza cu relatia de mai sus;
- Wp este dublul modulului de rezistenta la incovoiere (Wi).
Rezulta: t = -8410 MPa.
Tensiunile principale s si s se determina cu expresiile:
s s ![]() (5.106)
(5.106)
unde s se introduce cu semnul care rezulta din relatia de definitie. Semnul pozitiv in fata radicalului corespunde tensiunii principale s
Se determina tensiunea echivalenta (sech) cu teoria de rezistenta a tensiunilor tangentiale maxime:
sech s s
in care s si s se introduc cu semnele ce rezulta din relatia (5.106)
Se calculeaza coeficientul de siguranta la oboseala care dupa Serensen are expresia:
c = s bk eg sv ysm (5.107)
in care:
s este rezistenta la oboseala pentru un ciclu simetric de incovoiere s sr sr pentru fonta avand valoarea 700 MPa, deci s = 210 MPa
bk coeficient de concentrare al tensiunilor care se poate lua egal cu 2;
e coeficient dimensional e = 0,7
- g coeficient de calitate al suprafetei g
y coeficient de material y
sv si sm sunt amplitudinea tensiunii si tensiunea medie:
sm smax smin
Inlocuind valorile in relatiile de mai sus obtinem:
sv = 90,7 MPa
sm= 65,75 MPa
Vom obtine c = 1,81
c) Calculul bratului
Pe langa eforturile Mv, Mh si Mt, in brat apare si efortul axial N. Aceste eforturi variabile in timp, solicita bratul la oboseala prin incovoiere in planul cotului si perpendicular pe planul cotului, prin torsiune si prin intindere-compresiune.
Momentul Mh determina tensiunea normala sih care variaza liniar pe inaltimea sectiunii si valoarea maxima este data de relatia:
sih = Mh/Wz (5.109)
in care Wz = h b2 /6. Momentul incovoietor Mv determina tensiunile siv care variaza liniar pe inaltimea sectiunii si valoarea maxima se calculeaza cu relatia:
siv = Mv/Wy (5.110)
in care, Wy = b h2 /6
Momentul de torsiune Mt determina tensiuni tangentiale txy si txz care se calculeaza cu relatiile:
txy = Mt/(k1 b h ); txy = k2 txy
Forta axiala N determina tensiuni normale st constante pe suprafata sectiunii transversale. Aceste tensiuni se calculeaza cu relatia:
st = N/A (5.111)
in care N =Zs - Frcg , iar A este aria sectiunii transversale a bratului.
Deoarece celelalte eforturi Mv, Mt si N sunt constante pe lungimea bratului, sectiunea periculoasa este data de existenta concentratorilor de tensiune care se afla la racordarea dintre fusuri si brat.
Prin suprapunere de efecte se calculeaza tensiunea normala de incovoiere si compresiune:
s siv st (5.112)
Daca in relatia (5.112) se inlocuiesc (5.110) si (5.111) se obtine:
s = Mv/Wy + N/A
Daca se tine seama ca N = Zs+FRcg rezulta:
s = Zs(6a/b h + 1/b h) + FRcg/b h
Tensiunile maxime si minime se determina cu relatiile:
smin = Zsmin(6a/b h2 + 1/b h) + FRcg/b h (5.113)
in care:
- Zsmin = 1156 N;
- a = (lp+h)/2 = 48 mm;
- h = 173 mm;
- b = 40,3 mm
smax= Zsmax(6a/b2 h + 1/b h) + Frcg/b h (5.114)
in care:
- Zsmax= 1156N;
- a =(lp+h)/2 = 48 mm;
- h =173 mm;
- b = 40,3 mm
Inlocuind valorile obtinem:
smin = 131,57 MPa; smax = 441,98 MPa
Tensiunea tangentiala txy este:
txy =T a/2k1 b h (5.115)
Forta T fiind variabila determina tensiunile variabile:
tmax = Tmax a/2k1 b h; tmin = Tmin a/2k1 b h (5.116)
in care:
- Tmax = 38477,58 N , Tmin = -17806,66 N;
- a = (lp+h)/2 = 48 mm;
- h = 173 mm;
- b = 40,3 mm.
Inlocuind valorile obtinem:
tmax=5945 MPa; tmin=-5184 MPa
Considerand ciclurile tensiunilor s si t periodice si in faza se determina coeficientul de siguranta global pentru solicitari compuse:
c = cs ct/ cs + ct (5.117)
Coeficientul de siguranta partial cs se calculeaza cu relatia:
cs s bks esg sv yssm (5.118)
in care:
s este rezistenta la oboseala pentru un ciclu simetric de incovoiere s = 1120 MPa
- es coeficient dimensional e
g coeficient de calitate al suprafetei g
ys coeficient de material ce se calculeaza cu relatia ys s so so
sv si sm sunt amplitudinea tensiunii si tensiunea medie:
sv smax smin
sm smax smin
Inlocuind valorile in relatiile de mai sus obtinem:
sv = 907 MPa; sm= 657,55 MPa
Coeficientul de concentrare al tensiunilor bks se calculeaza ca produs al unor coeficienti care tin seama, fiecare in parte, de influenta unor factori:
(
bkt bkt)ref bt)b bt)h bt)s bt)e
in care:
- (bks)ref coeficientul de concentrare a eforturilor unitare la incovoiere pentru cotul de referinta (bks)ref = 2,15
- (bs)b coeficient de corectie care tine seama de latimea bratului (bs)b=1,1
- (bs)dMi coeficient de corectie care tine seama de diametrul interior al gaurii din fusul maneton (bs)dMi = 0,9
- (bs)e coeficient de corectie care tine seama de excentricitatea gaurii din fusul maneton (bs)e
- (bs)s coeficient de corectie care tine seama de suprapunerea "s" a fusurilor maneton (bs)s
- (bs d coeficient de corectie care tine seama de grosimea "d bs d
- (bkt)ref coeficientul de concentrare a eforturilor unitare la torsiune in punctul de racordare (bkt)ref
- (bt)b coeficientul de corectie care tine seama de latimea bratului (bt)b
- (bt)h coeficientul de corectie care tine seama de grosimea bratului (bt)h
- (bt)s coeficientul de corectie care tine seama de suprapunerea fusurilor (bt)s
- (bt)e coeficientul de corectie care tine seama de excentricitatea "e" a gaurilor din fusul maneton (bt)e
Inlocuind valorile coeficientilor se obtine:
bks bkt
Deci cs
Coeficientul de siguranta ct se calculeaza cu relatia:
ct t bkt etg tv yttm (5.120)
in care:
t este rezistenta la oboseala pentru un ciclu simetric de torsiune si este egal cu 50MPa;
et coeficient dimensional et
g coeficient de calitate al suprafetei g
yt coeficient de material ce se calculeaza cu relatia yt t to to
tv si tm sunt amplitudinea tensiunii si tensiunea medie:
(
tm tmax tmin
Inlocuind valorile in relatiile de mai sus obtinem:
tv tm=5.04 MPa
- coeficientul de concentrare al tensiunilor bkt se calculeaza cu relatia de mai sus.
Inlocuind valorile obtinem:
ct
Coeficientul de siguranta total va fi:
c = cs ct/ cs+ct, deci c = 2,03 (5.122)
Coeficientul de siguranta calculat trebuie sa fie cuprins in intervalul 23.
|
Politica de confidentialitate |
| Copyright ©
2024 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |