
Calculul modal cu considerarea comportarii spatiale a structurilor
1. Generalitati
In cazul constructiilor care prezinta o distributie neuniforma a maselor si a rigiditatilor elementelor structurale, deplasarile si eforturile se vor determina printr-un calcul spatial, capabil de a considera deformatiile spatiale structurale.
Calculul raspunsului seismic structural, reprezentat de eforturi si deplasari, se poate realiza prin integrarea directa a ecuatiilor de miscare sau prin suprapunerea raspunsurilor modale maxime.
Actiunea seismica se schematizeaza printr-o translatie variabila in timp a bazei de rezemare intr-o directie determinata, descrisa printr-o accelerograma. Aceasta produce oscilatii de translatie si de torsiune. Caracterul nesincron al miscarii seismice aplicat bazei structurii genereaza oscilatii de torsiune, chiar si in cazul structurilor perfect simetrice. Ca urmare, pentru a obtine valorile majorate ale deplasarilor si eforturilor datorate nesincronismului miscarii seismice este necesara descrierea actiunii seismice si prin acceleratii de torsiune la nivelul bazei de rezemare. In cazul analizei modale spectrale, acceleratiile de translatie si de torsiune generate de actiunea seismica se inlocuiesc cu spectre de raspuns de proiectare distincte asociate celor doua componente de miscare.
Calculul spatial permite o evaluare mai
realista a efectelor actiunii seismice in raport cu metodele de
calcul plan. Prin integrarea ecuatiilor de miscare pentru un set
adecvat de accelerograme, calculul dinamic spatial furnizeaza un
volum mare de informatii si necesita un efort substantial in
interpretarea si utilizarea rezultatelor. Din acest motiv, in prezenta
anexa se prezinta numai metoda determinarii raspunsurilor
modale maxime prin intermediul spectrului de raspuns de proiectare. Raspunsurile modale
maxime se combina probabilistic prin una din cele doua metode
cunoscute, SRSS (radical din suma patratelor raspunsurilor modale)
sau CQC (combinare patratica completa). In anumite situatii, cand doua perioade proprii de
vibratie succesive se afla in relatia Ti+1 ![]() 0.9 Ti,
raspunsurile modale se combina prin adunarea valorilor absolute (abssum).
0.9 Ti,
raspunsurile modale se combina prin adunarea valorilor absolute (abssum).
Metoda de calcul cu spectre de raspuns poate fi descoperitoare atunci cand contributiile raspunsurilor modale sunt exprimate prin factori de echivalenta a maselor modale efective avand valori sub 0,6-0,7. In acest caz, eforturile si deformatiile se limiteaza inferior la valorile furnizate de calculul plan.
Efectuarea de calcule pe modele spatiale este necesara in cazul constructiilor de importanta ridicata si care prezinta discontinuitati in ceea ce priveste distributia elementelor de rezistenta si a maselor de nivel. Acestea sunt precizate in capitolul 4.
Relatiile de calcul sunt stabilite in aceleasi ipoteze si au o forma asemanatoare cu relatiile din capitolul 4.
Raspunsul spatial considera simultan efectul oscilatiilor de translatie si de torsiune, echivalate simplificat printr-un calcul in doua etape in care efectele obtinute prin calcul plan se combina cu efectele torsiunii generale exprimate printr-o excentricitate generata de pozitiile diferite ale centrului de masa si centrului de rigiditate si de efectul asincron al undelor seismice.
In ipoteza planseelor indeformabile in planul lor, ecuatiile de miscare caracteristice unei actiuni seismice sunt de forma
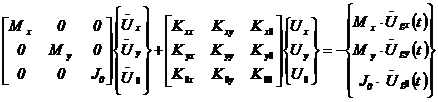 (c1)
(c1)
in care s-au neglijat efectele amortizarii structurale, ale cuplajelor inertiale si ale vibratiilor verticale.
Mx si My reprezinta matricele diagonale ale maselor, üx(t), y(t) vectorii acceleratiilor, iar Ux si Uy vectorii deplasarilor de translatie pe directiile x si y.
J0, üq(t), Uq(t) reprezinta matricea diagonala a maselor de rotatie, respectiv vectorii acceleratiilor unghiulare si ai rotirilor asociate vibratiilor de torsiune in jurul unei axe verticale z. Deplasarile si acceleratiile sunt exprimate in centrele maselor (figura C1).
![]() sunt componente ale
matricei de rigiditate structurale raportate la centrele maselor.
sunt componente ale
matricei de rigiditate structurale raportate la centrele maselor.
![]() sunt vectorii
acceleratiilor de translatie, respectiv de rotatie a bazei de
rezemare generate de miscarea terenului.
sunt vectorii
acceleratiilor de translatie, respectiv de rotatie a bazei de
rezemare generate de miscarea terenului.
In cazul unor structuri care nu sunt simetrice in raport cu planele xoz si yoz, ecuatiile de miscare si implicit vibratiile structurii sunt cuplate elastic prin termenii matricei de rigiditate.
Prin urmare, raspunsul
sistemului structural la componentele miscarii terenului pe directia
x sau y va include urmatoarele deplasari suplimentare:
translatie in directia y sau x, precum si torsiune
generala a planseelor in jurul axei verticale, chiar in absenta
unor acceleratii unghiulare a bazei constructiilor (![]() ). Cuplarea vibratiilor modale de translatie
si de torsiune se identifica prin valori nenule ale factorilor de
participare a maselor modale efective.
). Cuplarea vibratiilor modale de translatie
si de torsiune se identifica prin valori nenule ale factorilor de
participare a maselor modale efective.
In cazul unor structuri simetrice, la care centrele de rigiditate coincid cu centrele maselor si cu acceleratii unghiulare nule ale bazei de rezemare, ecuatiile de miscare se decupleaza pentru cele trei directii principale de oscilatie, asa cum rezulta din relatia:
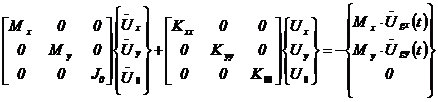 (C2)
(C2)
In aceasta situatie, torsiunea generala nu este prezenta (Uq ).
Efectele rotirii bazei din nesincronismul undelor seismice, precum si ale eventualelor distributii neuniforme a maselor, diferite de cele admise in modelele de calcul, se vor obtine prin aplicarea fortelor seismice modale de nivel intr-o pozitie diferita de cea a centrului maselor de nivel si definita de excentricitatea accidentala.
In lipsa unui spectru de torsiune de proiectare, factorii de participare a maselor modale efective asociati vibratiilor de torsiune pot fi corectati in functie de viteza echivalenta de propagare a undelor seismice Ve, de dimensiunile bazei de rezemare si de perioadele proprii de vibratie.
Calculul modal spatial se realizeaza cu programe de calcul automat care pot considera numai efectul de torsiune generala produs de necoincidenta pozitiei centrelor maselor cu pozitia centrelor de rigiditate, nu si efectul de torsiune generala produs de nesincronismul undelor seismice.
C2. Determinarea incarcarilor, eforturilor si deplasarilor seismice
In cazul vibratiilor spatiale, fortele seismice de calcul asociate fiecarui mod de vibratie se stabilesc cu relatii compatibile cu relatiile prezentate in capitolul 4 pentru calculul plan.
Forma deformatei, definita de pozitia deplasata a centrelor maselor, este in general o curba stramba in spatiu ca urmare a cuplajelor generate de distributia neuniforma a rigiditatilor si a maselor. In consecinta, fortele seismice asociate gradelor de libertate dinamica considerate vor avea orientari diferite in raport cu sistemul general de axe in care este descrisa structura, indiferent de directia actiunii seismice. Fiecarui grad de libertate dinamica ii corespunde o componenta, forta seismica statica echivalenta, pentru fiecare mod de vibratie considerat.
In general, intr-un punct nodal definit de intersectia a cel putin doua elemente structurale, se considera patru grade de libertate dinamica (figura C1), trei de translatie pe directiile axelor generale ce definesc structura (ux, uy, uz) si o rotatie in jurul axei normale la baza de rezemare (qz daca baza de rezemare se gaseste in planul orizontal xOy, cu axa z verticala).
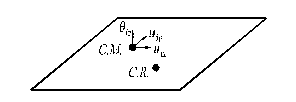 M. = centrul maselor
M. = centrul maselor
R. = centrul de rigiditate
Fig. C1 Grade de libertate dinamica
la nivelul "i" in
ipoteza planseului indeformabil in planul sau
La determinarea raspunsului structural la actiuni seismice se pot distinge doua situatii:
structuri cu plansee indeformabile in planul lor,
structuri cu plansee deformabile sau fara plansee.
Pentru fiecare din cele doua situatii se pot considera sau nu cuplajele inertiale. Absenta cuplajelor inertiale determina o matrice a maselor diagonala care contine numai masele de translatie si de rotatie corespunzatoare gradelor de libertate dinamica acceptate in model. In cazul general, cand sunt prezente cuplaje inertiale, matricea maselor nu este diagonala.
2.2. Calculul raspunsului modal spatial la actiuni seismice se poate efectua in urmatoarele ipoteze :
neglijarea cuplajelor inertiale,
planseele sunt indeformabile (rigide) in planul lor,
neglijarea influentei componentei verticale a miscarii seismice a terenului,
actiunea seismica este reprezentata prin miscarea terenului in directia uneia din axele orizontale x sau y sau intr-o directie oarecare in planul bazei de rezemare,
la fiecare nivel centrele maselor si centrele de rigiditate sunt distincte si se pot afla sau nu pe aceeasi verticala; prin unirea lor rezulta fie o axa verticala dreapta, fie o linie poligonala stramba in spatiu,
in centrul maselor se considera trei grade de libertate dinamica, doua translatii ux si uy in directiile axelelor x si y si o rotire uq in directia axei verticale z,
masele se reduc in centrul maselor (fig. C2), rezultand :
masa de translatie de nivel
![]() (C3)
(C3)
masa de rotatie de nivel
![]() (C4)
(C4)
in care n
= numarul de mase discrete concentrate mi,j sau distribuite pe suprafetele ![]()
dj = distanta din centrul maselor la pozitia masei concentrate mi,,j ,
r
= distanta de la centrul maselor la o masa elementara ![]() ,
,
i = indice de nivel, de la 1 la N,
N = numarul total de niveluri ale constructiei.
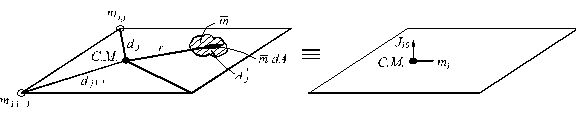 Fig. C2
Fig. C2
In cazul unei mase ![]() distribuite
uniform pe toata suprafata planseului se obtin :
distribuite
uniform pe toata suprafata planseului se obtin :
![]() - masa de
translatie la nivelul i
- masa de
translatie la nivelul i
![]() - masa de
rotatie fata de axa z la nivelul i
- masa de
rotatie fata de axa z la nivelul i
unde A = aria planseului,
Ip = Ix+Iy momentul de inertie polar al suprafetei planseului fata de centrul maselor.
Pentru un mod de vibratie k, se definesc urmatoarele marimi:
masa modala generalizata in modul de vibratie k
![]() (C5)
(C5)
unde ![]()
![]() si
si ![]() sunt componentele vectorului propriu in modul
de vibratie k, la nivelul i, pe directiile x, y
si z, respectiv.
sunt componentele vectorului propriu in modul
de vibratie k, la nivelul i, pe directiile x, y
si z, respectiv.
factorii de participare modali
![]()
![]() (C6)
(C6)
![]()
masele modale efective
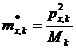
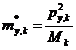
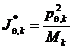 (C7)
(C7)
factorii de participare a maselor modale efective (coeficienti de echivalenta modali)
![]()
![]()
![]() (C8)
(C8)
unde
![]() si
si ![]() (C9)
(C9)
sunt rezultantele maselor de translatie si de rotatie aplicate la toate nivelurile structurii.
In cazul unei actiuni seismice definite printr-un spectru de proiectare Sdx=Sd asociat unei miscari de translatie a bazei intr-o directie paralela la una din axele globale x sau y se dezvolta urmatoarele forte seismice de baza modale (figura C3):
![]()
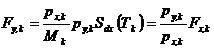
si momentul de torsiune (C10)
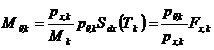
Pentru fiecare mod propriu de vibratie, pe directiile gradelor de libertate ux, uy, uq la fiecare nivel, in centrul maselor se dezvolta urmatoarele forte seismice de nivel (figura C4).
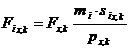
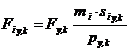 (C11)
(C11)
si momentul de torsiune
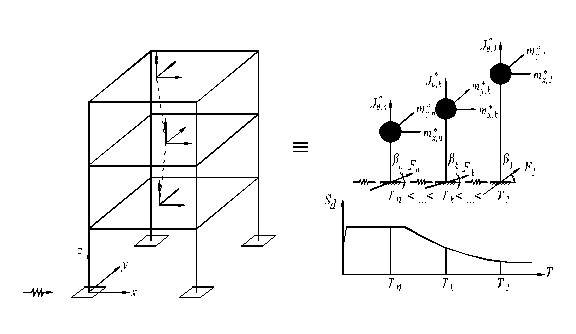
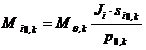
Fig. C3 Sistem structural spatial si sistemele modale echivalente
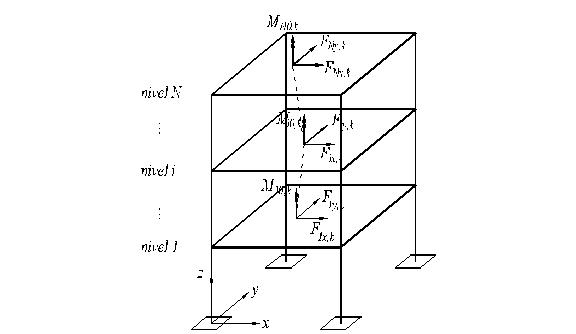
Fig. C4 Forte seismice de nivel in modul k de vibratie
Pentru o miscare de translatie a terenului in directia y, Sdy=Sd fortele seismice modale de baza sunt:
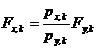
![]() (C12)
(C12)
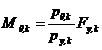
In aceasta situatie, fortele seismice modale de nivel, se obtin cu relatiile (C10) de mai sus.
In cazul unei miscari seismice descrise ca o translatie a terenului intr-o directie a fata de axa x (figura C5), fortele seismice de baza se obtin cu relatiile precedente in care
![]() (C13)
(C13)
![]()
Fig. C5
Fortele seismice modale de baza si de nivel se obtin prin sumarea algebrica a fortelor rezultate pentru cele doua componente spectrale Sdx si Sdy.
Pentru
structurile care au numai mase de translatie discrete si grade de
libertate dinamice de translatie independente (fara
legaturi indeformabile), relatiile de calcul sunt similare cu cele de
mai sus, in care se anuleaza masele de rotatie (![]() si
si ![]() ).
).
C3. Observatii finale
In relatiile de mai sus nu este inclus efectul unei miscari nesincrone a bazei de rezemare. In calculul modal spatial se recomanda ca efectele nesincronismului undelor seismice si ale unor eventuale distributii neuniforme a maselor, diferite de cele adoptate in modelul de calcul, sa fie considerate prin introducerea unei excentricitati accidentale asociate fortelor seismice modale. Se obtine astfel un caz suplimentar de incarcare statica numai cu momente de torsiune aplicate in centrul maselor de la fiecare nivel. Raspunsul din acest caz suplimentar de incarcare se combina cu raspunsul obtinut prin suprapunere modala. Combinarea raspunsurilor se va efectua astfel incat sa se obtina valori maxime pentru raspunsul total.
Semnele eforturilor si deplasarilor obtinute prin suprapunere modala se vor considera identice cu cele obtinute pentru modul fundamental de vibratie.
In situatia in care coeficientul de echivalenta corespunzator modului fundamental de vibratie este mai mic de 0.7, raspunsul structural obtinut prin combinare modala se va controla printr-un calcul dinamic liniar.
Miscarea seismica descrisa prin spectrul de raspuns de proiectare trebuie considerata cel putin in directiile principale asociate structurii. Acestea sunt definite de directia rezultantei fortei seismice de baza din modul fundamental si de normala pe aceasta directie.
Relatiile din aceasta anexa sunt stabilite in ipoteza unei baze rigide la interfata teren-structura, pentru care se poate accepta o miscare de corp rigid unidirectionala. In cazul unor fundatii izolate si departate, se poate considera pentru fiecare grad de libertate de la interfata structura-teren, miscari defazate ale terenului. In aceasta situatie sunt necesare calcule speciale, care includ efectele nesincrone ale miscarii seismice prin matrici de corelatie spatiala definite pentru ficare grad de libertate de la interfata teren-structura.
|
Politica de confidentialitate |
| Copyright ©
2024 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |