
L'analyse de l'indice de développement humain utilisant des méthodes économétriques
1. La description des variables
L'indice du developpement humain (IDH)
L'indice du développement humain (IDH) est un indice statistique composite, créé par le Programme des Nations Unies pour le Développement (PNUD) en 1990, évaluant le niveau de développement humain des pays du monde.
Le concept du développement humain est plus large que ce qu'en décrit l'IDH qui n'en est qu'un indicateur créé par le PNUD pour évaluer ce qui n'était mesuré auparavant qu'avec imprécision. L'indicateur précédent utilisé, le PIB par habitant, ne donne pas d'information sur le bien-être individuel ou collectif, mais n'évalue que la production économique. Il présente des écarts qui peuvent être très importants avec l'IDH.
L'IDH est un indice composite, compris entre 0 (tres faible) et 1 (excellent), calculé par la moyenne de trois indices:
v la santé /longévité (mesurées par l'espérance de vie à la naissance), qui permet de mesurer indirectement la satisfaction des besoins matériels essentiels tels que l'accès à une alimentation saine, à l'eau potable, à un logement décent, à une bonne hygiène et aux soins médicaux.
v le savoir ou niveau d'éducation. Il est mesuré par le taux d'alphabétisation des adultes (pourcentage des 15 ans et plus, sachant écrire et comprendre aisément un texte court et simple traitant de la vie quotidienne) et le taux brut de scolarisation (mesure combinée des taux pour le primaire, le secondaire et le supérieur). Il traduit la satisfaction des besoins immatériels tels que la capacité à participer aux prises de décision sur le lieu de travail ou dans la société ;
v le niveau de vie (logarithme du produit intérieur brut par habitant en parité de pouvoir d'achat), afin d'englober les éléments de la qualité de vie qui ne sont pas décrits par les deux premiers indices tels que la mobilité ou l'accès à la culture.
On peut calculer l'IDH apres la formule suivante:
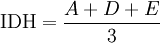
ou D= indices de longévité
E=niveau de vie.
|
Indice |
Mesure |
Valeur minimale |
Valeur maximale |
Formule |
|
Longévité |
espérance de vie à la naissance (EV) |
25 ans |
85 ans |
A = |
|
Education |
Taux d'alphabétisation (TA) |
D = |
||
|
Taux brut de scolarisation (TBS) | ||||
|
Niveau de vie |
logarithme du PIB par habitant en parite de pouvoir d'achat |
100 USD |
40.000 USD |
E= |
2. La représentation graphique
3. La spécification du modèle IDH, indice d'espérance de vie, indice de niveau d'instruction:
y=a+bx1+cx2.
Ou : y = IDH
x1= indice d'esperance de vie
x2 = indice de niveau d'instruction
4. L'estimation des paramètres
Conformément au tableau « La régression entreIDH, l' indice d'esperance de vie et l'indice de niveau d'instruction », les valeurs de paramètres sont les suivantes :
a = -0.341453715
b = 0.73537364
c = 0.638297518
Y= -0.34+ 0.73X1+ 0.64X2 (valeur theoretique)
5. La vérification des paramètres
5.1.La discussion économétrique du modèle
Le test ,,t''
Pour tester la
validité des paramètres a, b, c, il est nécessaire d'établir les deux
hypothèses (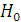
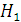
La valeur du ,,t'' du tableau Student correspondant à n -k =30-2=28 et α=0,05 est égale à 2,048.
Pour le paramètre ,,a'' on a :
H0 : a=0 ;
H1 : a<>0.
T calculé pour a est -5.8004668 qui est plus grand en module que 2,048, alors on accepte l'hypothèse H1 (a est significativement différent de 0).
Pour le paramètre ,,b'' on a :
H0 : b=0 ;
H1 : b<>0.
T calculé pour b est 16.5107328 qui est plus grande en module que 2,048, alors on accepte l'hypothèse H1 (b est significativement différent de 0).
Pour le paramètre ,,c'' on a :
H0 : c=0 ;
H1 : c<>0.
T calculé pour c est 10.1296979 qui est plus grande en module que 2,048, alors on accepte l'hypothèse H1 (c est significativement différent de 0).
Donc les trois valeurs en modules sont plus grandes que 2,048, ce qui signifie que les variables a, b et c sont significativement différents de '0'.
5.2. Le calcul de l'intervalle de confiance pour les paramètres
a appartient ( a- sa*tcritique ; a+ sa*tcritique) , sa*tcritique = 0.058866592*2,048= 0.12
a appartient a l'intervalle ( -0.46 ; -0.22)
b appartient ( b- sb*tcritique ; b+ sb*tcritique) , db = sb*tcritique = 0.044539128*2,048= 0.09
b appartient a l'intervalle ( 0.56 ; 0.83)
c appartient ( c- sc*tcritique ; c+ sc*tcritique) , dc = sc*tcritique = 0,063012493*2,048= 0.13
c appartient a l'intervalle ( 0.51 ; 0.77)
5.3. L'analyse économique du modèle
Si l'indice du niveau d'espérance de vie est égale a 0 et l'indice du niveau d'instruction est égale a 0 alors la valeur de l'IDH est négative (-0.341453715).
Si l'indice du niveau d'espérance de vie est égale a zéro et la valeur de l'indice du niveau d'instruction se modifie avec une unité alors la valeur de l'IDH se modifie avec 0.64.
Si l'indice du niveau d'instruction est égale a 0 et la valeur de l'indice du niveau d'espérance de vie se modifie avec une unité alors la valeur de l'IDH se modifie avec 0.74.
5.4. L'analyse de la qualité du modèle
Pour la validation du modèle choisi, on a utilisé le test Fischer qui suppose deux hypothèses :
H0 :
H1 :
Pour cela on a du obtenir la valeur du F calculé qui est le rapport entre MSR (la variance ajustée avec le degré de liberté) et MSE(la variance ajustée des erreurs) :
On doit chercher la valeur du F critique :
Fcritique = F 0,05 ;dfr ;df
dfr= 2
df
Fcritique = F 0,05 ;2 ;27= 3,35
La valeur de Fcalcule> la valeur de F critique (du tableau Fischer) donc on peut accepter la première hypothèse H1. Le modèle est viable et l'indice d'espérance de vie et l'indice du niveau d'instruction sont des facteurs essentiels qui influencent l'évolution de l'IDH.
La valeur du R2 (le rapport de détermination) est égale à 0,954236319 ce qui signifie que 95% de la variation des IDH est expliquée par l'influence des indices.
La valeur du R(coefficient de corrélation linéaire) est égale à 0,976850203 ce qui signifie que entre le IDH et les deux indices il y a une liaison forte.
5.5. Le teste Durbin-Watson
d1 du tableau Durbin-Watson (pour α=0,05) correspondant a p=2 (le nombre de variables exogènes) et n=30 (le nombre d'observations) est : d1=1.35
d2 du tableau Durbin-Watson (pour α=0,05) correspondant a p=2 (le nombre de variables exogènes) et n=30 (le nombre d'observations) est : d2=1.49
4- d1 =2.65
4- d2 =2.51
Décisions :
DW=
6. Modèle unifactoriel IDH-indice d'espérance de vie
6.1. La vérification des paramètres
6.1.1. La discussion économétrique du modèle
Le test ,,t''
Pour tester la validité des paramètres a, b, il est nécessaire d'établir les deux hypothèses (nulle et alternative) pour chaque paramètre, de calculer la valeur du ,,t'' et de la comparer avec ,,t'' du tableau Student.
La valeur du ,,t'' du tableau Student correspondant à n -k =30-1=29 et α=0,05 est égale à 2,045
Pour le paramètre ,,a'' on a :
H0 : a=0 ;
H1 : a<>0.
T- calculé pour a est 1,653836(t stat) qui est plus petit en module que 2,045, alors on accepte l'hypothèse H0 (a n'est pas significativement différent de 0).
Pour le paramètre ,,b'' on a :
H0 : b=0 ;
H1 : b<>0.
T- calculé pour b est 9,972755 qui est plus grande en module que 2,045, alors on accepte l'hypothèse H1 (b est significativement différent de 0).
6.1.2. La spécification du modèle IDH, Indice d'espérance de vie
y= bx1 = 0.89* x1
Ou y= IDH
x1= indice d'espérance de vie
Alors on a : b= 0,894353169
6.1.3. Le calcul de l'intervalle de confiance pour les paramètres
b appartient ( b- sb*tcritique ; b+ sb*tcritique) , sb*tcritique = 0,0896796532 (standard error)*2,045= 0.18
b appartient a l'intervalle ( 0.71 ; 1.23)
6.2. L'analyse économique
Si la valeur de l'indice d'espérance de vie est égale à 0 alors la valeur de l'IDH sera 0.
Par contre si la valeur de l'indice d'espérance de vie se modifie avec une unité , la valeur de l'IDH va se modifier dans le même sens avec 0.89.
6.3. L'analyse de la qualité du modèle
Pour la validation du modèle choisi, on a utilisé le test Fischer qui suppose deux hypothèses :
H0 :
H1 :
Pour cela on a du obtenir la valeur du F calcule qui est le rapport entre MSR(la variance ajustée avec le degré de liberté)et MSE (la variance ajustée des erreurs) :
On doit chercher la valeur du F critique :
Fcritique = F 0,05 ;dfr ;df
dfr= 1
df
Fcritique = F 0,05 ;1 ;28= 4.20
La valeur de Fcalcule> la valeur de F critique (du tableau Fischer) donc on peut accepter la première hypothèse H1. Le modèle est viable et l'indice d'espérance de vie est un facteur qui influence l'évolution de l'IDH.
La valeur du R2 (le rapport de détermination) est égale a 0,78031605 ce qui signifie que 78% de la variation des IDH est expliquée par l'influence de l'indice.
La valeur du R(coefficient de corrélation linéaire) est égale a 0,8833550 ce qui signifie que entre le IDH et l'indice il y a une liaison forte.
6.4. Le teste Durbin-Watson
d1 du tableau Durbin-Watson (pour α=0,05) correspondant a p=1 (le nombre de variables exogènes) et n=30 (le nombre d'observations) est : d1=1.35
d2 du tableau Durbin-Watson (pour α=0,05) correspondant a p=1 (le nombre de variables exogènes) et n=30 (le nombre d'observations) est : d2=1.49
4- d1 =2.65
4- d2 =2.51
Décisions :
DW= 0.044 n'appartient pas a l'intervalle (d2=1,49 ; 4- d2=2,51) , donc les erreurs sont dépendantes (sont auto corrélées).
7. Modèle unifactoriel IDH-indice du niveau d'instruction
7.1. La vérification des paramètres
7.1.1. La discussion économétrique du modèle
Le test ,,t''
Pour tester la validité des paramètres a, c il est nécessaire d'établir les deux hypothèses (nulle et alternative) pour chaque paramètre, de calculer la valeur du ,,t'' et de la comparer avec ,,t'' du tableau Student.
La valeur du ,,t'' du tableau Student correspondant à n -k =30-1=29 et α=0,05 est égale à 2,045
Pour le paramètre ,,a'' on a :
H0 : a=0 ;
H1 : a<>0.
T- calculé pour a est -0,288948 (t stat) qui est plus petit en module que 2,045, alors on accepte l'hypothèse H0 (a n'est pas significativement différent de 0).
Pour le paramètre ,,c'' on a :
H0 : c=0 ;
H1 : c<>0.
T- calculé pour c est 5,2094363 qui est plus grande en module que 2,045, alors on accepte l'hypothèse H1 (c est significativement différent de 0).
7.1.2. La spécification du modèle IDH, Indice d'espérance de vie
y= cx2 = 1.004* x2
Ou y= IDH
x2= indice du niveau d'instruction,
Alors on a : c= 1.004
7.1.3. Le calcul de l'intervalle de confiance pour les parametres
c appartient ( c- sc*tcritique ; c+ sc*tcritique) , sc*tcritique = 0,1838915 (standard error)*2,045= 0.38
c appartient a l'intervalle ( 0.62 ; 1.38)
7.2. L'analyse économique
Si la valeur de l'indice du niveau d'instruction est égale a 0 alors la valeur de l'IDH sera 0.
Par contre si la valeur de l'indice du niveau d'instruction se modifie avec une unité , la valeur de l'IDH va se modifier dans le même sens avec 1.004.
7.3. L'analyse de la qualité du modèle
Pour la validation du modèle choisi, on a utilisé le test Fischer qui suppose deux hypothèses :
H0 :
H1 :
Pour cela j'ai du obtenir la valeur du F calcule qui est le rapport entre MSR(la variance ajustée avec le degré de liberté) et MSE(et la variance ajustée des erreurs) :
On doit chercher la valeur du F critique :
Fcritique = F 0,05 ;dfr ;df
dfr= 1
df
Fcritique = F 0,05 ;1 ;28= 4.2
La valeur de Fcalcule> la valeur de F critique (du tableau Fischer) donc on peut accepter la première hypothèse H1. Le modèle est viable et l'indice du niveau d'instruction est un facteur qui influence l'évolution de l'IDH.
La valeur du R2 (le rapport de détermination) est égale a 0,49218534 ce qui signifie que 49% de la variation des IDH est expliquée par l'influence de l'indice.
La valeur du R(coefficient de corrélation linéaire) est égale a 0,70155922 ce qui signifie que entre le IDH et l'indice il y a une liaison forte.
7.4. Le teste Durbin-Watson
d1 du tableau Durbin-Watson (pour α=0,05) correspondant a p=1 (le nombre de variables exogènes) et n=30 (le nombre d'observations) est : d1=1.35
d2 du tableau Durbin-Watson (pour α=0,05) correspondant a p=1 (le nombre de variables exogènes) et n=30 (le nombre d'observations) est : d2=1.49
4- d1 =2.65
4- d2 =2.51
Décisions :
DW= 0.24 n'appartient pas a l'intervalle (d2=1,49 ; 4- d2=2,51) , donc les erreurs sont dépendantes (sont auto corrélées).
8. Conclusions
Le premier modèle unifactioriel n'est pas viable a cause du fait que les erreurs sont auto corrélées. De même la valeur du rapport de détermination est inferieure a celle du modèle bifactoriel.
Pour le deuxième modèle unifactoriel, c'est-à-dire IDH-indice du niveau d'instruction les erreurs sont toujours auto corrélés ce qui nous indique que le modèle qui explique mieux la corrélation entre les deux indices et l'IDH c'est le modèle bifactoriel.
Il a un rapport de détermination en proportion de 95% par rapport a 49% et 78% pour les modèles unifactoriels.
Donc notre choix est le modèle bifactoriel pour le fait qu'il montre que seulement les deux indices ensemble influencent en grand proportion l'IDH.
9. Annexes
1. Le modèle bifactoriel :
|
Valeur de l'indicateur du developpement humain (IDH) |
Indice d'espérance de vie |
Indice de niveau d'instruction |
||
|
Norvège | ||||
|
Islande | ||||
|
Irlande | ||||
|
Suède | ||||
|
Suisse | ||||
|
Pays-Bas | ||||
|
Finlande | ||||
|
| ||||
|
Belgique | ||||
|
Autriche | ||||
|
| ||||
|
Italie | ||||
|
Royaume-Uni | ||||
|
Espagne | ||||
|
Allemagne | ||||
|
Grèce | ||||
|
Slovénie | ||||
|
| ||||
|
Chypre | ||||
|
Malte | ||||
|
Hongrie | ||||
|
Pologne | ||||
|
Estonie | ||||
|
Lituanie | ||||
|
Slovaquie | ||||
|
Croatie | ||||
|
Lettonie | ||||
|
Bulgarie | ||||
|
Roumanie | ||||
|
Bosnie-Herzégovine |
La régression entre IDH, l'indice d'espérance de vie et l'indice de niveau d'instruction:
|
SUMMARY OUTPUT |
|
|
Regression Statistics |
|
|
Multiple R | |
|
| |
|
Adjusted | |
|
Standard Error | |
|
Observations | |
|
ANOVA | |||||
|
df |
SS |
MS |
F |
Significance F |
|
|
Regression |
8.261E-19 |
||||
|
Residual |
| ||||
|
Total | |||||
|
Coefficients |
Standard Error |
t Stat |
P-value |
Lower 95% |
Upper 95% |
Lower 95.0% |
Upper 95.0% |
|
|
Intercept |
3.5849E-06 | |||||||
|
X 1 |
1.2339E-15 | |||||||
|
X 2 |
1.0761E-10 |
|
RESIDUAL OUTPUT | ||
|
Observation |
Predicted Y |
Residuals |
|
9.6658E-05 |
||
|
Y |
Y |
|
|
( |
( |
|
5.041E-05 |
|||||
|
3.721E-05 |
|||||
|
6.084E-05 |
|||||
|
1E-04 |
6.241E-05 |
1E-08 |
|||
|
1.296E-05 |
1.369E-05 |
||||
|
1.369E-05 |
|||||
|
6.4E-07 |
|||||
|
9.61E-06 |
|||||
|
8.41E-06 |
3.6E-05 |
||||
|
9.025E-05 |
|||||
|
3.6E-07 |
|||||
|
9.025E-05 |
|||||
|
2.025E-05 |
2.5E-05 |
||||
|
2.5E-07 |
3.025E-05 |
||||
|
8.281E-05 |
1.296E-05 |
||||
|
4.41E-06 | |||||
|
6.084E-05 |
|||||
|
6.889E-05 |
2.5E-07 |
||||
|
8.281E-05 |
7.396E-05 |
||||
|
1.024E-05 |
|||||
|
1.936E-05 |
1.44E-06 |
||||
|
9.025E-05 |
|||||
|
8.281E-05 |
1.6E-07 |
||||
0.00734159 0.00347479
2. Le modèle unifactoriel IDH-indice d'espérance de vie
|
Valeur de l'indicateur du developpement humain (IDH) |
Indice d'espérance de vie |
||
|
Norvège | |||
|
Islande | |||
|
Irlande | |||
|
Suède | |||
|
Suisse | |||
|
Pays-Bas | |||
|
Finlande | |||
|
| |||
|
Belgique | |||
|
Autriche | |||
|
| |||
|
Italie | |||
|
Royaume-Uni | |||
|
Espagne | |||
|
Allemagne |
|
||
|
Grèce | |||
|
Slovénie | |||
|
| |||
|
Chypre | |||
|
Malte | |||
|
Hongrie | |||
|
Pologne | |||
|
Estonie | |||
|
Lituanie | |||
|
Slovaquie | |||
|
Croatie | |||
|
Lettonie | |||
|
Bulgarie | |||
|
Roumanie | |||
|
Bosnie-Herzégovine |
La régression entre IDH et l'indice d'espérance de vie
|
SUMMARY OUTPUT |
|
|
Regression Statistics |
|
|
Multiple R | |
|
| |
|
Adjusted | |
|
Standard Error | |
|
Observations | |
|
ANOVA | ||||||||
|
df |
SS |
MS |
F |
Significance F | ||||
|
Regression |
1.022E-10 | |||||||
|
Residual | ||||||||
|
Total | ||||||||
|
Coefficients |
Standard Error |
t Stat |
P-value |
Lower 95% |
Upper 95% |
Lower 95,0% |
Upper 95,0% |
|
|
Intercept | ||||||||
|
X Variable 1 |
1.022E-10 |
|
RESIDUAL OUTPUT |
|
|||||||
|
||||||||
|
Observation |
Predicted Y |
Residuals |
|
|||||
|
||||||||
|
||||||||
|
||||||||
|
||||||||
|
||||||||
|
||||||||
|
||||||||
|
||||||||
|
||||||||
|
||||||||
|
||||||||
|
||||||||
|
||||||||
|
||||||||
|
||||||||
|
||||||||
|
||||||||
|
||||||||
|
||||||||
|
||||||||
|
||||||||
|
||||||||
|
||||||||
|
||||||||
|
||||||||
|
||||||||
|
||||||||
|
||||||||
|
||||||||
|
||||||||
|
Y |
Y |
|
|
( |
( |
|||
|
4E-06 | ||||||||
|
7.921E-05 | ||||||||
|
8.41E-06 | ||||||||
|
4.41E-06 | ||||||||
|
9.801E-05 | ||||||||
|
4.41E-06 | ||||||||
0.02402223 0.543556
0.0441946
3. Le modèle unifactoriel IDH et l'indice du niveau d'instruction
|
Valeur de l'indicateur du developpement humain (IDH) |
Indice de niveau d'instruction |
||
|
Norvège | |||
|
Islande | |||
|
Irlande | |||
|
Suède | |||
|
Suisse | |||
|
Pays-Bas | |||
|
Finlande | |||
|
| |||
|
Belgique | |||
|
Autriche | |||
|
| |||
|
Italie | |||
|
Royaume-Uni | |||
|
Espagne | |||
|
Allemagne | |||
|
Grèce | |||
|
Slovénie | |||
|
| |||
|
Chypre | |||
|
Malte | |||
|
Hongrie | |||
|
Pologne | |||
|
Estonie | |||
|
Lituanie | |||
|
Slovaquie | |||
|
Croatie | |||
|
Lettonie | |||
|
Bulgarie | |||
|
Roumanie | |||
|
Bosnie-Herzégovine |
La régression entre IDH et l'indice de niveau d'instruction:
|
SUMMARY OUTPUT |
|
|
Regression Statistics |
|
|
Multiple R | |
|
| |
|
Adjusted | |
|
Standard Error | |
|
Observations | |
|
Coefficients |
Standard Error |
t Stat |
P-value |
Lower 95% |
Upper 95% |
Lower 95,0% |
Upper 95,0% |
|
|
Intercept | ||||||||
|
X Variable 1 |
1.5646E-05 |
|
ANOVA | |||||
|
df |
SS |
MS |
F |
Significance F |
|
|
Regression |
1.56458E-05 |
||||
|
Residual | |||||
|
Total |
|
RESIDUAL OUTPUT | ||
|
Observation |
Predicted Y |
Residuals |
|
Y |
Y |
|
|
( |
( |
||
|
2.54016E-05 |
|||||||
|
2.54016E-05 |
|||||||
|
4.624E-05 | |||||||
|
1.538E-06 | |||||||
|
6.46416E-05 |
|||||||
|
4.9E-05 |
|||||||
|
8.24464E-05 |
|||||||
0.1196902 0.028519506
0.2382777
10. Bibliographie
Tanasoiu Ovidiu , ed. ASE, Bucuresti, 1998 - 'Econometrie : studii de caz '
Pecican,Eugen , Tanasoiu Ovidiu, ed. ASE, Bucuresti, 2001 - 'Modele econometrice'
Voineagu Virgil, ed. Meteor Press , Bucuresti, 2007 - 'Teorie si practica econometrica'
www.data.un.org
www.epp.eurostat.ec.europa.eu
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |