
Transformata Fourier si cristalografia de raze X
Cea mai mare putere a rezolutiei pentru determinarea structurilor macromoleculelor si complexelor macromoleculare
Matematic: transformata Fourier si inversa ei convertesc dintre doua domenii ("spatii") r (exemplu: spatiu sau timp) si domeniul k (exemple: momente sau frecvente)
Aplicatie: metoda de reduce a zgomotului
1. Transformata Fourier a unui obiect zgmotos
2. Se substituie anumite componente de amplitudine mica din transformata Fourier
3. Se face transformata Fourier inversa
Imaginea de difractie a cristalului este trasformata Fourier a structurii
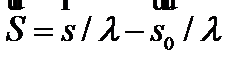
Difractia pe un singur punct
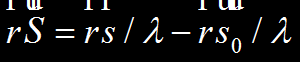
Difractia pe doua obiecte punctiforme
Interferenta constructiva daca rS=0,+1, +2,
Interferenta destructiva daca rS=+1/2, +3/2,
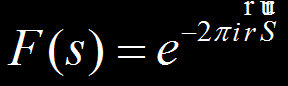 Imaginea de difractie F(S) este data
de:
Imaginea de difractie F(S) este data
de:
Pentru un obiect macroscopic constand din mai multe puncte cu diverse puteri de imprastiere:
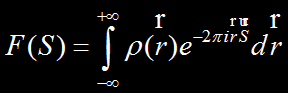
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |