
Algoritmi de scheletizare (subtierea)
Multe forme, mai ales cele subtiri, pot fi descrise prin versiunile lor subtiate, alcatuite din linii conectate, aflate, in mod ideal, de-a lungul axei mediane a formelor.
Desenele compuse din linii sau caractere de text trebuie sa fie digitizate la o rezolutie suficient de mare pentru ca liniile sa nu fie intrerupte sau terminatiile lor sa se piarda. La o astfel de rezolutie este posibil ca pe unle portiuni liniile sa aiba latimea mai mare ca 2 pixeli.
Scheletizarea permite refacerea structurii liniare a figurii digitizate, fara distrugerea conectivitatii.
Axa mediana sau axa schelet a unei regiuni este definita in planul continuu (analogic) astfel:
Fie R o regiune in planul continuu, C conturul regiunii si P un punct din R.
Cel mai apropiat vecin al lui P pe C este un punct M cu proprietatea ca nu exista alt punct in C a carui distanta fata de P sa fie mai mica decat PM. Daca P are mai multi vecini in C cu aceasta proprietate, atunci P este un punct de schelet al lui R
Reuniunea punctelor de schelet formeaza axa schelet sau axa mediana a lui R.
Din definitie rezulta ca punctele schelet sunt centre ale unor cercuri continute in intregime in R, cu proprietatea ca nu exista alte cercuri cu aceleasi centre, de raza mai mare, continute in R.




![]()
Transpunerea conceptului de axa mediana in planul discret este dificila deoarece drumul intre 2 pixeli nu este unic si nu poate fi aplicata definitia distantei euclidiene dintre 2 pixeli.
Nu exista o definitie matematica a procesului de scheletizare, dar exista numerosi algoritmi.
Scheletizarea (subtierea) poate fi definita euristic ca o
succesiune de erodari ale marginilor unei forme pana cand se obtine scheletul
formei Algoritmii de scheletizare sunt algoritmi iterativi care
indeparteaza pixelii de contur, adica pixelii de tranzitie 0 ![]() 1 intr-o imagine binara. Totodata, pixelii
sunt indepartati astfel incat conectivitatea formei sa fie mentinuta.
1 intr-o imagine binara. Totodata, pixelii
sunt indepartati astfel incat conectivitatea formei sa fie mentinuta.
Algoritmii de scheletizare trebuie sa satisfaca urmatoarele constrangeri:
Sa conserve conectivitatea in fiecare iteratie pentru aceasta sunt eliminati pixelii de contur care ar putea cauza discontinuitati, de exemplu, pixelul marcat in figura (a).
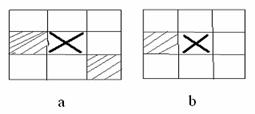
Algoritm de scheletizare
Consideram imaginea binara.
In fiecare iteratie se viziteaza o singura data fiecare pixel al imaginii, verificandu-se daca poate fi indepartat, cu satisfacerea celor 2 constrangeri.
Pentru aceasta se cerceteaza vecinatatea de 8 pixeli a fiecarui pixel interior regiunii (P=1). Fie urmatoarea notatie:
|
P8 |
P1 |
P2 |
|
P7 |
P |
P3 |
|
P6 |
P5 |
P4 |
se numara pixelii interiori din vecinatatea lui P (inreg);
- daca inreg ![]() 2, P nu poate fi eliminat din regiune caci el
apartine unei
2, P nu poate fi eliminat din regiune caci el
apartine unei
Terminatii sau conecteaza 2 parti ale unei forme;
- daca inreg = 8, P nu poate fi indepartat, deoarece aceasta ar conduce
la erodarea formei;
- daca 2< inreg<8:
o
Se
numara tranzitiile 0 ![]() 1 din vecinatatea lui P: P8, P1, P2, P3, P4,
P5, P6, P7,P8
1 din vecinatatea lui P: P8, P1, P2, P3, P4,
P5, P6, P7,P8
o Daca nrtranz = 1 inseamna ca in fereastra de 3x3 pixeli exista o singura componenta conectata. In acest caz se poate indeparta pixelul din centru caci indepartarea sa nu afecteaza conectivitatea locala a celorlalti pixeli din fereastra.
Algoritmul se termina atunci cand in ultima iteratie nu s-a mai indepartat nici un pixel.
void subtiere1 ( imagine x, int N1, int M1, int N2, int M2 )
}
}
} while (!gata);
Dezavantajul algoritmului este ca nu subtiaza imaginea simetric. Daca imaginea este parcursa pe randuri si de la stanga la dreapta liniile obiectului subtiat sunt localizate in partea de sud -- est a marginii obiectului, deoarece pixelii de frontiera din partile de nord - vest sunt eliminati primii. De aceea, rezultatul produs de algoritm nu este satisfacator atunci cand obiectele din imagini sunt relativ mari si convexe.
Se poate obtine o subtiere simetrica aplicand o varianta a algoritmului care opereaza in doi pasi, alternativi.
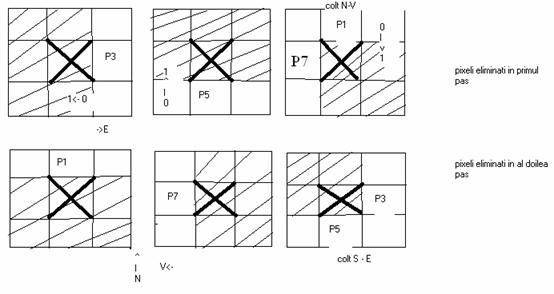
In primul pas sunt eliminati pixelii care apartin unei frontiere de est sau de sud sau unui colt de Nord - Vest.
In pasul al doilea sunt elimati cei care apartin unei frontiere de nord sau de vest sau unui colt de sud - est.
Notam cu :
N(P0) numarul de pixeli interiori din vecinatatea de 3 x 3 a pixelului curent, P0
T
(P0) numarul de tranzitii 0 ![]() 1 in secventa de pixeli care formeaza
periferia ferestrei: p1, p2, p3, ., p8,p1
1 in secventa de pixeli care formeaza
periferia ferestrei: p1, p2, p3, ., p8,p1
Atunci cele 2 conditii de eliminare a pixelilor in cei doi pasi sunt exprimate prin predicatele:
Pas 1 :
( 2 < N (P0) < 8 ) && T ( P0 ) == 1 && ( P3 == 0 || P5 == 0 || (P1 == 0 && P7 == 0))
Pas2 :
( 2 < N (P0) < 8 ) && T ( P0 ) == 1 && ( P1 == 0 || P7 == 0 || (P3 == 0 && P5 == 0))
In fiecare pas, pixelii care indeplinesc conditia de a fi eliminati sunt marcati pentru eliminare si numai dupa parcurgerea intregii imagini sunt eliminati.
void subtiere2 (imagine x, int N1, int M1, int N2, int M2)
else // pas =1
if ( y[1] == 0 || y[7] == 0 || (y[3] == 0 && y[5] == 0))
} //if inreg
}
//se elimina din regiune pixelii marcati
for ( k = N1 + 1; k< N2 - 1; k++ )
for ( l = M1 + 1; k< M2 - 1; l++ )
if ( z[k-N1-1] [l -M1-1] == 1 ) x[k][l] = 0;
} while (!gata);
*delocare matrice z
Algoritm de scheletizare bazat pe notiunea de pixel multiplu
Scheletul unei regiuni este o regiune liniara deci o regiune alcatuita numai din pixeli multipli.
Algortimii clasici de scheletizare considera drept pixeli schelet pixelii multiplii care satisfac conditia (1) din definitia pixelului multiplu (vezi "Regiuni liniare in spatiul discret"), adica satisfac unul dintre cele 6 sabloane.
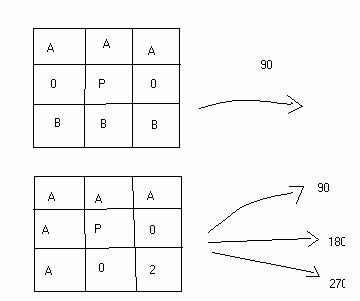
Intr-un grup de pixeli marcati cu aceeasi litera cel putin unul are valoarea diferita de zero.
Imaginea de intrare este binara. Se considera ca pixeli de contur pixelii care au un vecin-d egal cu zero. Numai pixelii de contur pot fi pixeli de schelet.
In fiecare iteratie se parcurge imaginea marcand pixelii de contur si pixelii de schelet, pe toate cele 4 laturi ale fiecarei regiuni existente in imagine. Dupa ce toata imaginea a fost traversata, pixelii marcati ca fiind de contur sunt eliminati (li se da valoarea zero).
In descrierea algoritmului se apeleaza functia sablon care primeste coordonatele unui pixel si indicele unuia dintre cele 6 sabloane. Functia intoarce 1 daca vecinatatea pixelului satisface sablonul.
Exemplu:
0 2 0 A A A
0 P 0 satisface sablonul 0 P 0
1 0 0 B B B
void subtiere3 (imagine x, int N!, int M1, int N2, int M2)
}
}// for D
//se elimina pixelii de contur
if ( !gata )
for ( k = N1 + 1; k<N2 - 1; k ++ )
for ( l = M1 + 1; l < M2 - 1; l ++ )
if ( x[k] [l] = = 2 )
x[k][l] = 0;
} while (!gata)
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |