
1. Conceptul de modalitate. Aspecte generale
Am spus inca din Introducere ca rostul principiilor logice este si acela de-a produce diferite simplificari (idealizari). De pilda, simplificarea produsa de principiul tertului exclus consta in faptul ca, potrivit principiului, propozitiile sunt impartite in doua mari clase - clasa propozitiilor adevarate si clasa propozitiilor false. O propozitie apartine obligatoriu uneia dintre clase, este exclusa a treia posibilitate.
La o privire mai atenta ne dam seama ca realitatea logica este mult mai complexa si ca nu orice propozitie este fie adevarata, fie falsa.
Nici chiar propozitiile adevarate nu sunt adevarate toate in acelasi fel. Unele sunt adevarate dar ar putea fi foarte bine si false; altele, in schimb, sunt adevarate si nu pot fi decat adevarate. Pentru a lamuri chestiunea sa luam cateva exemple:
1) Timisoara este cel mai mare oras din vestul Romaniei.
2) Toti celibatarii sunt necasatoriti.
3) In anul 2150 Romania va fi o mare democratie.
4) Orice numar par mai mare ca doi este suma a doua numere prime.
Propozitiile 1) si 2) sunt ambele adevarate insa adevarul lor nu este de acelasi fel. Despre propozitia 1) se spune ca este factual adevarata, in timp ce 2) este necesar sau logic adevarata.
Adevarul primei propozitii se intemeiaza pe corespondenta cu realitatea, o realitate care, in timp, se poate modifica. Desi adevarata in prezent, s-ar putea candva ca propozitia sa nu mai fie adevarata.
Si a doua propozitie corespunde realitatii numai ca, indiferent cum se modifica aceasta realitate, propozitia ramane mereu adevarata. Adevarul ei se datoreaza intelesului termenilor care o compun, iar corespondenta cu realitatea este consecinta modului in care se raporteaza intre ei acesti termeni. Propozitia din aritmetica "7 + 5 = 12" (exemplul lui Kant) este, de asemenea, necesara.
Negatia unei propozitii factual adevarate este factual falsa, iar negatia unei propozitii necesar adevarate este necesar falsa (ea este, fie o contradictie, fie o propozitie care implica o contradictie).
Propozitia 3) se refera la evenimente viitoare si contingente gen "Maine va fi o batalie navala" (exemplul lui Aristotel). Considerata astazi, propozitia nu este nici adevarata, nici falsa, ci doar posibila.
In fine, propozitia 4) s-ar putea sa fie adevarata, insa, pentru ca nu a fost inca demonstrata vom spune despre ea ca nu este cunoscuta ca adevarata. In aceeasi situatie se gasea pana nu de mult Marea teorema a lui Fermat, care, dupa demonstratia lui Andrew Wills (1992) a devenit un adevar matematic cunoscut.
Exemplele pe care le-am enumerat, si lista ar putea continua inca, ne obliga sa introducem in raport cu adevarul si falsul o serie de nuantari: necesar adevarat, posibil adevarat, cunoscut ca adevarat, necunoscut, adevar cert, incert si multe altele.
Aceste expresii se numesc in logica "modalitati", iar propozitiile care contin astfel de modalitati fac obiectul logicii modale.
Exista in momentul de fata mai multe tipuri de modalitati pe care le putem grupa in cateva categorii mari:
Modalitati aletice: necesar, posibil, contingent si imposibil.
Modalitati deontice: obligatoriu, permis, interzis, indiferent.
Modalitati temporale: intotdeauna, candva, uneori, niciodata etc.
Modalitati epistemice: cunoscut, necunoscut, verificat, indoielnic etc.
Modalitati existentiale: existent, nonexistent, vid, real, potential etc.
Modalitato probabiliste: probabil, improbabil, cert, incert etc.
Modalitati doxastice: cred, mi se pare, sunt convins etc.
Logica modala (ca disciplina) cuprinde: logica (teoria) modalitatilor aletice, logica deontica, logica temporala, logica epistemica, logica existentiala, logica probabilista, logica doxastica si probabil ca lista trebuie sa ramana deschisa. Se intelege ca nu toate aceste "logici" sunt independente si nici la fel de elaborate (de referinta este logica modalitatilor aletice, ea constituie "nucleul" logicii modale).
In limba greaca "aletheia" inseamna adevar, deci "modalitati aletice" inseamna "modalitati ale adevarului".
Cele mai importante modalitati aletice sunt cele deja introduse - necesar, posibil, imposibil si contingent - pentru desemnarea carora vom folosi de aici inainte notatiile: L (necesar), M (posibil), U (imposibil), si Q (contingent).
Discutiile despre modalitati incep in antichitate, Aristotel fiind autorul primului sistem de logica modala - silogistica modala.
Iata cateva dintre definitiile aristotelice mai importante date modalitatilor:
Ceea ce nu poate fi altfel decat este, il numim necesar.[1]
Posibilul insa - contrariul imposibilului - se iveste atunci cand contrariul sau nu este in chip necesar fals.[2]
Imposibilul este lucrul al carui contradictoriu este in chip necesar adevarat[3].
Expresia a fi contingent (posibil) se spune in doua moduri. Intr-un prim sens este ceea ce se intampla cel mai des si este lipsit de necesitate (.). In alt sens posibilul (contingentul) este nedeterminatul, ceea ce poate fi in acelasi timp astfel si altfel: de exemplu, a merge pentru un animal, sau inca, ca un cutremur sa se produca in timpul mersului sau, sau, intr-un chip mai general, ceea ce se intampla prin hazard[4].
Ceea ce observam din examinarea acestor definitii aristotelice ale modalitatii (plus multe altele pe care nu le-am mentionat aici) este ca:
1) Aristotel nu distinge intotdeauna aspectul logic de aspectul ontologic al modalitatii. Posibilul logic, de exemplu, se refera la adevarul propozitiilor, el inseamna "posibil adevarat", in timp ce posibilul ontologic se refera la lucruri sau la existenta, in general. Or, proprietatile celor doua forme de posibil nu sunt aceleasi, si chiar daca ar fi, distinctia tot trebuie facuta.
2) Nici aici, nici in alte contexte, Aristotel nu distinge posibilul de contingent (intamplator) de unde impresia ca la Aristotel apar patru denumiri si nu patru modalitati, ca numarul modalitatilor este de fapt trei (este o problema asupra careia voi reveni).
In orice caz, problema modalitatii il preocupa in cel mai inalt pe Aristotel, si nu numai pe el. Preocupari pe linia intelegerii modalitatilor intalnim si la megarici. De pilda, definitiile date de Diodorus Cronus modalitatilor angajeaza factorul timp, ele premerg logicii temporale de astazi:
Posibil = ceea ce este sau va fi adevarat.
Imposibil = ceea ce fiind fals nu va fi adevarat.
Necesar = ceea ce fiind adevarat nu va fi fals.
Nenecesar = ceea ce este deja fals sau va fi fals.
Ceva mai tarziu, stoicii vor redeschide discutia asupra modalitatilor insa dintr-o alta perspectiva. De la Diogenes Laertios ne-a ramas urmatoarea marturie despre modalitati in logica stoicilor.
Mai departe, unele lucruri sunt posibile, altele imposibile, unele necesare, altele nenecesare. Este posibil ceea ce admite sa fie adevarat, cu conditia ca nimic din imprejurarile externe sa nu-l impiedice de a fi adevarat, de exemplu: "Diocles traieste". Imposibil e ceea ce nu se admite sa fie adevarat, de exemplu: "Pamantul zboara". E necesar ceea ce, pe langa ca-i adevarat, nu admite sa fie fals sau, chiar daca admite sa fie fals, e impiedicat de a fi astfel de imprejurari exterioare, ca de exemplu: "Virtutea e utila". Nu-i necesar ca ceea ce este adevarat - putand fi totusi si fals -, daca nu sunt conditii exterioare care sa impiedice, de exemplu: "Dion se plimba". O propozitie verosimila este aceea care are mai multe sanse de a fi adevarata, de exemplu: "Voi fi in viata maine"[5].
Medievalii acorda, la randul lor, o mare atentie logicii modale. Incepand cu Toma D'Aquino, capitolul De modalibus apare in mai toate tratatele de logica medievala alaturi de alte cateva capitole importante - proprietates terminorum, insolubilia, consequentiae s.a.
Dintre autorii moderni, cel mai mare interes pentru problemele modalitatilor prezinta G. Leibniz si Im. Kant.
Leibniz distinge intre adevarurile necesare (pe care le mai numeste si "geometrice" sau "de ratiune") si adevarurile factuale sau "contingente". Distinctia lui va fi preluata, in alti termeni, si de Kant.
Tot de numele lui Leibniz se leaga si conceptul de "lume posibila", concept care apare la Leibniz in doua ipostaze.
Ipostaza logica: o propozitie este necesar adevarata daca este adevarata in toate lumile posibile.
Ipostaza teologica: de vreme ce Dumnezeu a creat aceasta lume, ea este cea mai buna dintre lumile posibile.
Ideea leibniziana de lume posibila va deveni tinta ironiilor lui Voltaire din romanul sau umoristic Candid (reamintesc ca prin "lume posibila", Leibniz intelegea o "lume pe care Dumnezeu ar fi creat-o dupa un alt plan").
In momentul de fata exista si o semantica a lumilor posibile (numita si semantica "in stil Kripke") care a generat o intreaga filosofie a lumilor posibile[6].
Primul autor care va relua problema modalitatii din perspectiva logicii formale moderne este Jan Lukasievicz. El demonstreaza ca logica modala nu se poate construi in cadrele stramte ale bivalentei ea necesitand o logica n-valenta (sau polivalenta). Am discutat acest lucru in Introducere, aici voi aduce doar unele completari.
Fie p si q doua propozitii din care formam propozitiile modale "Este necesar p" si "Este posibil q".
Strict vorbind, acestea sunt metapropozitii, ele afirma ceva despre alte propozitii. Reamintesc ca daca p apartine limbajului obiect, "Necesar p" apartine metalimbajului.
Presupunand ca "Necesar p" si "Posibil q" sunt adevarate, cum vor fi atunci p si q, adevarate sau false?
Conform schemei adevarului la Tarski, "Necesar p" este adevarata daca si numai daca p este necesara.
Dar atunci, necesarul apare intr-o dubla ipostaza: odata ca modalitate in propozitia "Necesar p", si altadata ca valoare de adevar a propozitiei p.
Pentru mai multa claritate vom proceda in maniera tabelelor de adevar din logica simbolica:

p Necesar p
![]()
..... fals
necesar adevarat
... fals
Observam ca in tabel, propozitia p are printre valorile ei si valoarea necesar, iar pentru aceasta valoare propozitia Necesar p este adevarata.
Reformulat: daca p = necesar, atunci Necesar p = adevarat. Iata o circularitate din care, pentru moment, nu putem iesi[7].
In acelasi fel a procedat Lukasiewicz cu definitia posibilului numai ca el a folosit notatii diferite pentru cele doua ipostaze ale posibilului estompand oarecum circularitatea definitiei:
|
p |
Mp |
In tabel, "1" reprezinta adevarul, "0" falsul, iar "˝" este posibilul. Ca si in cazul precedent, posibilul apare in doua ipostaze: prima (notata cu M) este modalitatea, a doua (notata ˝) este valoare de adevar.
Fac aici o paranteza pentru a reveni la problema negatiei.
Fie p o propozitie necesara sau posibila. Una este atunci negatia propozitiei p si cu totul alta negatia propozitiei "Este necesar p" sau "Este posibil p".
Presupunand ca p este propozitia "Patratul are patru laturi", negatia lui p va fi "Patratul nu are patru laturi" sau "Nu este adevarat ca patratul are patru laturi". Strict vorbind, acestea sunt propozitii contradictorii, ele afirma ca "Ceea ce are patru laturi nu are patru laturi" sau "Nu este adevarat ca ceea ce are patru laturi are patru laturi". Prin urmare, daca p este necesar adevarata, ~p este necesar falsa.
Altfel stau lucrurile in cazul propozitiilor "Necesar p" si "Posibil p" care sunt adevarate sau false, dar fara necesitate. Prin urmare, daca Lp este simplu adevarata, atunci ~Lp este simplu falsa, si invers; la fel pentru Mp si ~Mp.
Propozitia Lp se va citi: nu este necesar p (sau este contingent p), iar Mp se va citi: nu este posibil p (sau este imposibil p). Prin negatia necesarului, asadar, ajungem la contingent (intamplator), iar prin negatia posibilului la imposibil.
Cu toate neajunsurile lui, sistemul lui Lukasiewicz scoate in evidenta raportul foarte strans dintre modalitate si polivalenta (orice sistem modal presupune un sistem polivalent si orice sistem polivalent genereza (potential) un sistem modal)[8].
La putin timp dupa
Lukasiewicz, C.I. Lewis initiaza o noua directie in logica
modala avand ca punct de plecare de aceasta data problemele
implicatiei. El inlocuieste implicatia materiala (p q) cu implicatia stricta (p ![]() q) pe care o defineste prin "Nu este posibil p si non-q" (v. implicatia stricta, din cap. IV).
q) pe care o defineste prin "Nu este posibil p si non-q" (v. implicatia stricta, din cap. IV).
Cercetarile lui Lewis au impus un nou sistem de notatii pentru modalitati: (necesar), (posibil), (contingent) si (imposibil).
Sistemele implicatiei stricte (T, S1 - S5, B s.a.) sunt sisteme polivalente, chiar infinit valente si, dupa cum au demonstrat Gödel, Cohen s.a., in trecerea de la modalitate la polivalenta sistemele implicatiei stricte corespund diferitelor sisteme de logica intuitionista. Este un rezultat cu profunde semnificatii filosofice despre care s-a vorbit foarte mult la vremea respectiva..
Cum stau lucrurile astazi?
Exista, in momentul de fata, cel putin trei mari directii in dezvoltarea logicii modale.
Prima provine din logica lui Lukasievicz si trateaza modalitatea in dependenta de polivalenta. Se numeste "directia polivalenta (unii spun algebrica)" din dezvoltarea logicii modale.
A doua, numita "sintactica", isi are originea in lucrarile lui C.I. Lewis. Aici logica modala este prezentata sub forma unor sisteme sintactice (sau formale).
A treia directie, reprezentata de R. Carnap, S. Kripke, S. Kanger, J. Hintikka s.a, este directia semantica a logicii modale (asa numita semantica lumilor posibile). Este directia care se bucura de cea mai mare audienta la ora actuala.
Conceptele modale pot afecta propozitiile de predicatie in doua moduri: 1) prin plasarea modalitatii in afara propozitiei ca in exemplul "Este posibil ca unii studenti sa fie talentati", si 2) prin plasarea modalitatii in fata predicatului: "Unii studenti sunt posibil talentati".
Prima este o propozitie modala de dicto, a doua este o propozitie modala de re.
Propozitiile de dicto sunt formate din modus si dictum. In exemplul nostru modus-ul este modalitatea "posibil", iar dictum-ul "Unii studenti sunt talentati".
Aceeasi propozitie o putem exprima prin "Unii studenti sunt talentati este posibil adevarata" unde modalitatea apare la sfarsitul propozitiei. Nu conteaza deci unde este plasata modalitatea, conteaza ca ea sa afecteze propozitia ca intreg.
Aparent, intre forma de dicto si forma de re nu pare sa existe o diferenta prea mare si chiar s-a spus la un moment dat ca pentru propozitiile afirmative cele doua forme ale modalitatii sunt echivalente.
Nu cred ca este greu de gasit exemple care sa infirme aceasta pretentie. Fie propozitiile:
Toti jucatorii la Loto sunt posibil castigatori,
Este posibil ca toti jucatorii la Loto sa fie castigatori.
Prima este o propozitie modala de re si este adevarata. Ea spune ca fiecare jucator este un posibil castigator, altfel nimeni nu ar mai juca la Loto. A doua este o propozitie modala de dicto si este, evident, falsa pentru ca nu toti jucatorii castiga; dimpotriva, aproape toti pierd si doar o infima minoritate castiga. Prin urmare, nu orice modalitate de re se traduce printr-o propozitie de dicto echivalenta, si nici invers.
In general, modalitatile de dicto sunt considerate neproblematice, spre deosebire de modalitatile de re care intampina tot felul de obiectii.
Sa luam propozitia "x este necesar F". Ceea ce se predica aici despre x nu este pur si simplu F, ci necesar F care inseamna ceva mai mult decat F (una este sa spui despre cineva ca este vinovat si alta necesar vinovat).
Conceptia filosofica potrivit careia lucrurile au atat insusiri esentiale (sau necesare) cat si neesentiale este numita astazi esentialism (un prim reprezentant al esentialismului este chiar Aristotel).
Impotriva esentialismului s-au pronuntat in zilele noastre autori de prima marime printre care O. Quine si W. Kneale.
Sa examinam urmatorul rationament:
12 este in mod necesar compus
Numarul apostolilor = 12
Numarul apostolilor este necesar compus
De ce nu este valid acest rationament?
Daca principiul identitatii exprimat prin premisa a doua este in afara oricarei discutii, atunci explicatia nu poate fi cautata decat in prima premisa care exprima o necesitate de re. Asemenea propozitii, considera Kneale, sunt propozitii eliptice despre o necesitate relativa. Cu alte cuvinte, "x este necesar F" este o prescurtare pentru ceva de genul: "x este necesar F relativ la D", unde D este o descriptie.
Una si aceeasi proprietate este necesara in raport cu anumite descriptii si nenecesara in raport cu altele. De exemplu, daca Socrate este dat prin descriptia "filosoful grec care a fost sotul Xantipei", atunci el este necesar casatorit insa aceasta proprietate nu mai este necesara in raport cu descriptia "filosoful grec care a baut cucuta".
Concluzia lui Kneale este ca proprietatile nu pot fi necesare in general, ca necesitatea lor este intotdeauna relativa.
Iata si un alt argument, formulat de Quine.
Un ciclist, spune Quine, este necesar biped si contingent rational, in timp ce un matematician este necesar rational si contingent biped. Ce este atunci necesar si ce este contingent pentru un individ care este ciclist si matematician in acelasi timp?
Pentru multi autori aceste critici ale esentialismului, si implicit ale modalitatii de re, nu sunt convingatoare. Este cazul lui Alvin Plantinga, de exemplu, care promoveaza in cartea sa Natura necesitatii o interesanta forma de esentialism.
Intre altele, Plantinga considera necesitatea de dicto drept caz particular al necesitatii de re, astfel ca, odata ce am admis-o pe una automat am admis-o si pe cealalta. Iata, pe scurt, rationamentul lui Plantinga:
In schema "x este necesar F", variabila x poate sta pentru 9, iar F pentru "mai mare ca 7" ceea ce ar duce la propozitia necesara de re: "9 este necesar mai mare ca 7".
Dar x poate sta si pentru o propozitie, sa zicem, "7 + 5 = 12", iar F pentru predicatul "adevarat". In acest caz s-ar obtine propozitia modala de dicto: "7 + 5 = 12 este necesar adevarata".
Prin urmare, propozitiile modale de dicto se obtin din schema modalitatii de re, ele fiind un caz particular al acestora.
Dar atunci, se intreaba Plantinga, de ce propozitiile de re ar fi mai problematice decat propozitiile de dicto, de ce nu sunt ele la fel de problematice sau de neproblematice?
Dupa parerea mea, argumentul lui Plantinga nu este in afara oricarei obiectii.
Conform celor spuse, ar trebui ca x din schema "x este necesar F" sa fie atat variabila individuala cat si variabila propozitionala ceea ce, dupa stiinta mea, nu se poate. In logica modala a predicatelor ca, de altfel, in orice teorie logica, variabilele individuale si propozitionale sunt variabile distincte.
Nu spun prin aceasta ca modalitatea de re nu se mai justifica, ci doar ca argumentul lui Plantinga ridica o astfel de problema si ca, de aceea, justificarea modalitatii de re prin modalitatea de dicto pare foarte dificila.
4. 1. Definitiile aristotelice ale modalitatilor
Din problematica extrem de vasta a modalitatii voi discuta in aceasta carte doar patratul modalitatilor. Este vorba de sistemul de implicatii si inferente despre care am vorbit intr-un paragraf anterior, aplicat de data aceasta, propozitiilor modale. De exemplu, propozitia "Este imposibil p" implica propozitia "Nu este necesar p", iar propozitia "Este contingent ~p" este echivalenta cu propozitia "Posibil p".
Intrebarea este: putem avea un inventar complet al tuturor acestor implicatii si echivalente? Daca da, atunci ne va fi mult mai usor sa aratam care dintre inferentele cu propozitii modale sunt valide si care nu.
In capitolul 13 din Despre interpretare, Aristotel discuta pe larg aceste echivalente si implicatii dupa ce in capitolul anterior aratase cum se opun propozitiile modale. Curios este ca desi foloseste variabilele pentru termeni (v. Analitica Prima) el ezita sa introduca variabilele pentru propozitii.
Totusi, Aristotel produce o inovatie si in aceasta privinta. Pentru a face cat mai intuitive raporturile dintre modalitati, el simplifica la maxim propozitiile dictum astfel ca, in loc de "Este posibil p" sau "Nu este necesar non-p", el va spune: "Este posibil ca aceasta sa fie", respectiv, "Nu este necesar ca aceasta sa nu fie".
In loc de p, respectiv, ~p apar la Aristotel doua propozitii de o extrema simplitate: "sa fie", respectiv, "sa nu fie". Cu aceste simplificari Aristotel reuseste sa stabileasca patru clase de echivalenta in multimea propozitiilor modale, si anume:
|
C1 |
C3 |
|
|
Este posibil ca aceasta sa fie, Este contingent ca aceasta sa fie, Nu este imposibil ca aceasta sa fie, Nu este necesar ca aceasta sa nu fie. |
Nu este posibil ca aceasta sa fie, Nu este contingent ca aceasta sa fie, Este imposibil ca aceasta sa fie, Este necesar ca aceasta sa nu fie. |
|
C2 |
C4 |
|
|
Este posibil ca aceasta sa nu fie, Este contingent ca aceasta sa nu fie, Nu este imposibil ca aceasta sa nu fie, Nu este necesar ca aceasta sa fie. |
Nu este posibil ca aceasta sa nu fie, Nu este contingent ca aceasta sa nu fie, Este imposibil ca aceasta sa nu fie, Este necesar ca aceasta sa fie. |
Propozitiile din fiecare clasa sunt echivalente intre ele[9]. Aceasta inseamna ca una si aceeasi judecata poate fi exprimata prin mai multe propozitii, in functie de modalitatea avuta in vedere.
Conform notatiei adoptate, daca p inseamna "Este posibil ca aceasta sa fie", C1(p) este judecata exprimata de aceasta propozitie.[10]
Semnalez si o alta curiozitate in logica modala a lui Aristotel. In capitolul 12 din Despre interpretare el stabileste urmatoarele perechi de propozitii contradictorii:
Este posibil Nu este posibil
Este contingent Nu este contingent
Este imposibil Nu este imposibil
Este necesar Nu este necesar
Este adevarat Nu este adevarat
Din cate observam, adevarul si falsul sunt asezate in rand cu celelalte modalitati. Ideea este destul de stranie daca ne gandim ca "modalitati aletice" inseamna "modalitati ale adevarului".
Ce a avut in vedere Aristotel cand a facut aceasta enumerare?
Putem presupune ca in enumerarea lui au prevalat criterii formale si nu de continut avand in vedere ca atat adevarul, cat si falsul, pot functiona in forma de dicto sau in forma de re. De exemplu: "Este adevarat ca Socrate este filosof" si "Socrate este adevarat filosof" (sau "cu adevarat filosof"). La fel, in ce priveste falsul: "Este fals ca Dion este rege" si "Dion este fals rege".
Evident, propozitiile nu sunt echivalente insa constructii de acest sunt foarte frecvente. Precizez inca odata, este doar o ipoteza, textele lui Aristotel nu vorbesc despre asemenea propozitii.
4. 2. Problema raportului dintre contingent si posibil la Aristotel
Solutia lui Fl. Tutugan.
In tabelele lui Aristotel propozitiile "Este contingent p" si "Este posibil p" apar in aceeasi clasa, sunt propozitii echivalente. Preluata de logicienii medievali, echivalenta posibilului cu contingentul a intrat in traditia invatamantului logic fiind transmisa din generatie in generatie pana in sec. XX.
In primul volum din Dezvoltarea logicii, William si Martha Kneale deduc din aceasta echivalenta urmatoarea inconsistenta pe care o redau in forma simbolica:
Mp s Qp (premisa aristotelica),
Qp Q p (proprietate a contingentului),
Mp M p (aceeasi proprietate pentru posibil),
Lp Mp (implicatia posibilului de catre necesar),
Din 3) si 4) prin tranzitivitatea implicatiei rezulta:
5) Lp M p.
care inseamna: "Daca este necesar p, atunci este posibil p" (propozitie falsa). Prin urmare, din premisa aristotelica 1) si din alte propozitii modale adevarate rezulta propozitia falsa 5).
Ceva asemanator va demonstra, la noi, Florea Tutugan:
Mp s Qp (premisa aristotelica)
Qp s Lp (contigentul este negatia necesarului),
Mp s Up (posibilul este negatia imposibilului),
Din 2) si 3), prin 1), rezulta
Lp s Up din care, mai departe, rezulta
Lp s Up.
Cu alte cuvinte, daca posibilul este echivalent cu contingentul, atunci si necesarul va fi echivalent cu imposibilul.
Cum trebuie intelese cele doua modalitati pentru a evita aceste inconsistente? In general, cum trebuie definite modalitatile aletice pentru a putea construi un sistem consistent de logica modala?
Relativ la prima problema voi reproduce, foarte pe scurt, solutia logicianului roman Fl. Tutugan[11].
Solutia isi are punctul de plecare in analogia dintre propozitia de posibilitate Mp si propozitia particular afirmativa SiP. Asa cum exista doua sensuri ale particularei afirmative - un sens restrans si un sens larg - exista doua sensuri ale propozitiei de posibilitate.
Am spus ceva mai inainte ca "unii" din SiP poate insemna: 1) "Cel putin unii, nu este exclus toti" (sens larg), si 2) "Unii, exclus toti" (sens restrans).
In sens larg, SiP se opune lui SeP fara a o exclude pe SaP. In sens restrans, SiP se opune atat lui SaP cat si lui SeP.
In sens restrans, SiP este echivalenta cu SoP. Propozitia "Unii politicieni sunt corupti" implica (si este implicata de) propozitia "Unii politicieni nu sunt corupti", ceea ce nu se intampla cand propozitiile sunt luate in sens larg.
Exact la fel stau lucrurile cu propozitia de posibilitate. In sens larg, posibilul se opune imposibilului fara a exclude necesarul. In sens restrans, posibilul se opune atat necesarului cat si imposibilului.
La fel contingentul. In sens larg, el se opune necesarului fara a exclude imposibilul, iar in sens restrans, el se opune atat necesarului cat si imposibilului. Prin urmare, in sens restrans, posibilul este echivalent cu contingentul; nu si in sens larg pentru ca ar insemna ca si necesarul sa fie echivalent cu imposibilul.
Raporturile celor patru modalitati sunt redate de Fl. Tutugan cu ajutorul urmatoarei figuri:
![]()
![]()
![]() M
M
L |
M' |
U |
![]()
![]()
![]()
Q
Am notat, ca si pana acum, posibilul in sens larg cu M, iar posibilul in sens restrans (acelasi cu contingentul in sens restrans) cu M'. Acesta s-ar putea defini prin conjunctia dintre M si Q, respectiv: M'p =df Mp & Qp.
Se vede imediat ca posibilul in sens larg (M) se opune imposibilului (U), dar contine necesarul (L), tot asa cum contingentul in sens larg (Q) se opune necesarului (L), dar contine imposibilul (U).
In final, vom avea urmatoarele implicatii:
1) M'p Qp,
2) M'p Lp & Up
3) M'p Mp,
4) Up Qp,
5) Lp Mp,
O problema apare, totusi, in interpretarea lui Tutugan pentru ca imposibilul nu este intru totul simetric necesarului. In alti termeni, daca ceea ce este necesar este si posibil, nu se poate spune ca ceea ce este imposibil este si contingent (intamplator) intrucat imposibilitatea este, ea insasi, un fel de necesitate: Up =df L p. Daca, insa, prin contingent intelegem, ca mai sus, nonecesarul (ceea ce nu este necesar) atunci, intr-adevar, putem spune ca ceea ce este imposibil este si nonecesar (daca este imposibil p, atunci este nenecesar p).
Solutia lui Tutugan este de inspiratie aristotelica pentru ca si la Aristotel intalnim tot doua sensuri ale posibilului - un posibil in sens larg care include si necesarul (δυνατόν), si unul in sens restrans (ένδεχόμενον) care se opune atat necesarului cat si imposibilului. "Intrebuintez termenii «posibil» si «a fi posibil», spune Aristotel, despre ceea ce nu este necesar, dar nu duce la nimic imposibil, cand este dat"[12]. Ca de obicei, insa, Aristotel nu tine sa fie foarte riguros in utilizarea acestor modalitati.
O a doua analogie in definirea modalitatilor la Fl. Tutugan are ca punct de plecare distinctia dintre existenta si nonexistenta.
Stim din filosofie ca existenta poate fi necesara sau nenecesara (contingenta); la fel, nonexistenta.
Nonexistenta necesara este imposibilitatea, iar nonexistenta nenecesara este posibilitatea.
Contingenta va cuprinde atunci ceea ce exista dar care putea si sa nu existe, iar posibilitatea cuprinde ceea ce nu exista dar care, in alte conditii, putea exista.
Aceleasi distinctii le va face Tutugan pentru adevar si fals: adevar necesar, adevar nenecesar (contingentul), fals necesar (imposibilul) si fals nenecesar (posibilul). Impreuna cu posibilul si contingentul, luate in sens larg, el stabileste urmatoarea schema a modalitatilor:
![]()
![]()
![]() M
M
![]()
![]()
![]() A
A
L |
C |
P |
U |
F ![]()
![]()
![]()
![]()
![]()
Cu A s-a notat adevarul, in general (sau in sens larg), in care intra atat adevarul necesar (L) cat si adevarul contingent (C); F este falsul in general (sens larg) in care intra falsul necesar sau imposibilul (U) si falsul posibil (P); M si Q sunt posibilul, respectiv, contingentul, ambele in sens larg[13].
Iata si cateva din raporturile logice continute in schema lui Tutugan,:
1) Lp Ap,
2) Cp Mp,
3) Pp Fp,
4) Up Fp,
5) Up Qp,
6) Mp Lp Cp Pp,
7) Qp Cp Pp Up.
In baza acestor interpretari, autorul abordeaza si problema inferentelor cu propozitii modale, inclusiv silogistica modala. Din pacate, el nu a avut posibilitatea sa dezvolte aceste idei astfel ca mare parte din cercetarile lui in domeniul modalitatii au ramas in stadiul de proiect.
4. 3. Patratul clasic al modalitatilor.
In terminologia medievalilor propozitiile modale se compun, asa cum am mai spus, din modus si dictum. Modus-ul poate fi oricare din modalitatile enumerate, iar dictum-ul este propozitia pe care o afecteaza acest modus. In propozitia, "Este posibil sa ninga", modus-ul este modalitatea posibil, iar dictum-ul este propozitia "sa ninga".
Intr-o propozitie modala de dicto, negatia poate afecta: 1) modus-ul, 2) dictum-ul, 3) atat modus-ul cat si dictum-ul. Corespunzator, vor rezulta patru tipuri propozitionale notate de medievalii cu A, E, I, U:

m d
![]() A +
A +
E + -
I - +
U - -
![]()
In tabel, m inseamna modus, d inseamna dictum, + inseamna afirmativ si - negativ.
De exemplu, "Contingent p" ca si "Necesar p" sunt propozitii de tipul A (modus afirmativ si dictum afirmativ); in schimb, "Nu este imposibil non-p" este de tipul U (modus negativ si dictum negativ). La fel, "Nu este contingent non-p".
Cele patru tipuri propozitionale A, E, I, U se aplica fiecarei modalitati in parte astfel ca, in total, vor rezulta 16 propozitii modale. Rezumam aceste aplicatii cu ajutorul urmatorului tabel:

M Q U L |
|
|
E I U |
(1) (2) (3) (4) (5) (6) (7) (8) (9) (10) (11) (12) (14) (15) (16) |
Numerele din tabel indica intersectia dintre tipul propozitiei si modus. De exemplu, (7) este la intersectia lui E cu U, adica E(U).
Sa nu confundam, insa. Litera "E" din expresia E(U) este tipul propozitiei (= propozitie cu modus afirmativ si dictum negativ, cf. primului tabel), iar U este modalitatea imposibil. Prin urmare, E(U) nu inseamna altceva decat U p (Imposibil non-p).
Numarul (10) este la intersectia lui I cu Q , este deci I(Q). Cum I insemna propozitie modala cu modus negativ si dictum afirmativ, numarul (10) va desemna propozitia ~Qp (nu este contingent p).
Observam, de asemenea, ca in tabel modalitatile sunt date in ordinea M, Q, U, L. Nu este o ordine intamplatoare, este ordinea modalitatilor din clasele de echivalenta date de Aristotel.
Notam peste tot dictum-ul cu p si determinam propozitiile modale de la 1 la 16 in maniera deja exemplificata:
(1) = A(M) = Mp, (9) = I(M) = Mp
(2) = A(Q) = Qp, (10) = I(Q) = Qp
(3) = A(U) = Up, (11) = I(U) = Up
(4) = A(L) = Lp, (12) = I(L) = Lp
(5) = E(M) = M p (13) =U(M) = M p
(6) = E(Q) = Q p (14) = U(Q) = Q p
(7) = E(U) = U p (15) = U(U) = U p
(8) = E(L) = L p (16) = U(L) = L p
Cele saisprezece propozitii sunt, practic, propozitiile din clasele de echivalenta date de Aristotel, deci sunt echivalente patru cate patru. Prin urmare, daca doua propozitii x si y ar fi in raport de contrarietate, toate propozitiile echivalente cu x vor fi in raport de contrarietate cu toate propozitiile echivalente cu y. Acelasi lucru este valabil cu privire la celelalte raporturi ale patratului logic.
Pentru desemnarea (si determinarea) celor patru clase de echivalenta, medievalii au introdus cuvintele mnemotehnice:
PURPIREA
AMEBIMUS
EDANTULI
Cum se opereaza cu aceste cuvinte (formule)?
In primul rand observam ca in fiecare cuvant apar simbolurile A, E, I, U dar intr-o alta ordine: U, I, E, A (in Purpirea); A, E, I, U (in Amebimus), E, A, U, I (in Edantuli) si I, U, A, E(in Iluace).
Pentru determinarea celor patru clase de echivalenta aplicam aceste simboluri modalitatilor insa nu oricum, ci in ordinea data de Aristotel:
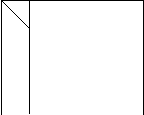
M Q U L
![]()
C1 U I E A
C2 A E I U
C3 E A U I
C4 I U A E
![]()
Cu ajutorul tabelului determinam acum componenta fiecarei clase de echivalenta in parte:
C1 =
C2 =
C3 =
C4 =
Sa mai observam ca in fiecare clasa exista o modalitate fara negatie. Aceasta va fi clasa modalitatii respective. Clasa C1, de exemplu, este clasa necesarului, aceasta clasa este determinata de Purpirea si stabileste toate propozitiile echivalente cu "Necesar p". Clasa C2, determinata de Amebimus, este clasa posibilului. Clasa C3 provine din Iluace si este clasa imposibilului, iar C4, generata de Edantuli, este clasa contingentului. Sintetic:
C1 = CL (Purpirea)
C2 = CM (Amebimus)
C3 = CU (Iluace)
C4 = CQ (Edantuli)
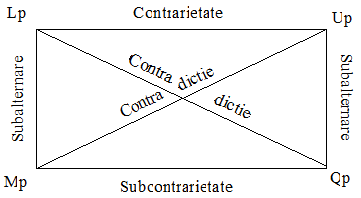
Tinand cont ca necesarul implica posibilul, se opune contingentului si ca este contrar imposibilului, putem stabili structura de patrat logic pentru modalitatile simple, fara negatie:
Daca adaugam la fiecare modalitate clasa ei de echivalenta obtinem o "compozitie" de mai multe patrate pe care le putem "comprima" intr-o singura figura de patrat:
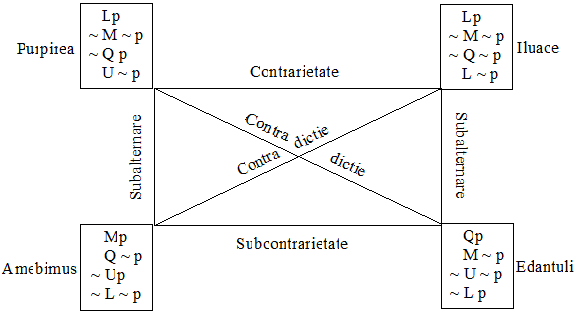
Pentru ca fiecare clasa de echivalenta contine patru propozitii, raporturile patratului logic se pot exprima in diverse moduri in functie de propozitia pe care o alegem. Iata cateva exemple:
● Raport de subalternare:
Lp Mp Up Qp
U p Q p L p M p
Qp L p Mp U p
● Raport de contrarietate:
Lp Up Up Lp
U p Mp Mp Qp
Qp L p L p U p
● Raport de subcontrarietate:
Mp Qp, Qp Mp
L p U p M p Up
Q p Lp Lp Q p
● Raport de contradictie:
Lp Qp Up = Mp
U p M p L p Q p
Qp = U p Mp = Up
Observatii. Cele patru raporturi ale patratului logic exemplificate aici sunt valabile numai daca prin contingent intelegem negatia necesarului. Daca prin contingent intelegem atat negatia necesarului cat si a imposibilului, atunci multe din aceste raporturi incepand cu subalternarea nu se mai mentin. Trebuie spus, pe de alta parte, ca in fixarea acestor raporturi medievalii au preluat echivalenta dintre posibil si contingent asa cum apare ea la Aristotel si ca, din aceasta cauza, cuvintele mnemothenice au la ei forme usor diferite: Purpurea, Amabimus, Iliace si Edentuli. Repetarea primei vocale in componenta fiecarui cuvant se explica tocmai prin faptul ca posibilul si contingentul genereaza, la Aristotel, aceeasi propozitie. (vezi si nota 20)
4. 4. Patratul modalitatilor aplicat propozitiilor de predicatie
Octogonul logic
Ce se intampla daca aplicam patratul modalitatilor propozitiilor de predicatie SaP, SeP, SiP, SoP care, si ele, formeaza un patrat logic?
Sigur ca, in acest caz, va rezulta o structura mult mai complexa rezultata din juxtapunerea mai multor structuri de patrat. De pilda, din combinarea subalternarilor Lp Mp si SaP SiP vor rezulta patru subalternari:
L(SaP) L(SiP), L(SaP) M(SiP)
L(SaP) M(SaP), M(SaP) M(SiP)
Acelasi lucru se intampla daca vom combina pe Lp Mp cu SeP SoP:
L(SeP) L(SoP), L(SeP) M(SoP)
L(SeP) M(SeP), M(SeP) M(SoP)
Intre L(SaP) si L(SeP) este raport de contrarietate, iar intre M(SiP) si M(SoP) este raport de subcontrarietate.
Cele opt propozitii formeaza octogonul logic (diagonalele indica raporturile de contradictie):
LA LE
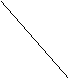

MI MO
Pentru simplificarea schemelor am notat propozitiile de predicatie cu A, E, I, O (fiecare diagonala corespunde unui raport logic). Se intelege ca propozitiile imposibile si cele contingente formeaza structuri similare, astfel ca, prin insumarea tuturor acestor raporturi va rezulta o structura mult mai complicata. Unitatea de baza a acestor structuri logice, oricat de complicate ar fi ele, este insa patratul logic
1. Ce este judecata, ce este propozitia si ce raporturi exista intre ele? Comentati afirmatia: "Judecata sta la acelasi nivel al limbajului cu notiunea, iar propozitia cu termenul".
2. Scrierti o scurta lucrare despre raportul dintre judecata si propozitie plecand de la textul lui Diogenes Laertios:
Judecata e ceea ce este adevarat sau fals sau un lucru complet in sine, care a luat in sine poate fi afirmat sau negat. Cum spune Hrysip in ale sale Definitii dialectice: "O judecata este ceea ce poate fi negat sau afirmat pentru sine", de exemplu: "E ziua"sau "Dion se plimba": Cuvantul grecesc pentru judecata deriva de la verbul "a judeca" prin care se arata acceptarea sau respingerea; caci, cand spui "Este ziua", pare sa accepti faptul ca este ziua. Daca este intr-adevar ziua, judecata din fata noastra este adevarata, iar daca nu e ziua, e falsa. Exista o deosebire intre judecata, intrebare si chestionare, ca si intre imperativ, juramant, optativ, hipotetic, vocativ, chiar daca acesti termeni sunt aplicati la un lucru asemanator cu o judecata. Judecata este ceea ce exprimam in vorbire si este o enuntare falsa sau adevarata; o intrebare este un lucru cu inteles deplin, ca si judecata, dar care cere un raspuns, de exemplu "E ziua?". Aceasta nu-i in sine nici adevarat, nici fals, asa incat: "E ziua!" este o afirmare, iar "E ziua?", o intrebare. O chestionare e un lucru la care nu se poate raspunde printr-un semn, asa cum poti afirma: "Da", la o intrebare, ci trebuie sa exprimam raspunsul in cuvinte: "Traieste in cutare loc".
Intrebarile, chestionarile si cele asemanatoare cu acestea nu sunt nici adevarate, nici false, pe cand judecatile propriu-zise sunt intotdeauna sau adevarate sau false[15].
Se dau propozitiile:
a) Anul trecut a avut loc o eclipsa totala de soare.
b) In urmatorii ani nivelul de trai va continua sa scada in Romania.
c) Dumineca la ora 7,00 incep alegerile locale.
d) Spectacolul a inceput la ora optspezece si s-a terminat la ora douazeci.
e) Actualul prim ministru poarta ochelari.
f) Nimeni nu credea ca si la noi se mai poate schimba ceva.
g) Radioactivitatea a crescut in ultimii ani peste limitele admise.
h) Apele multor rauri din vest au crescut peste limita de atentie.
Care dintre aceste propozitii sunt inchise, care sunt deschise si de ce?
4. Prin ce se deosebesc propozitiile de extensiune de propozitiile extensionale? Dar cele de intensiune de cele intensionale?
5. Dati exemple de propozitii compuse si aratati cand sunt adevarate aceste propozitii si cand sunt ele false.
Care dintre propozitiile de mai jos sunt neextensionale si in ce fel?
a) C. I. Lewis este cunoscut ca autorul povestirii Alice in tara minunilor.
b) Pana in sec. XX nu se stia ca lumina are greutate.
c)Este adevarat ca multi parlamentari sunt implicati in afaceri.
d) Probabil ca la viitoarele alegeri castiga opozitia.
e)Nu sunt foarte sigur ca Marea teorema a lui Fermat este corect demonstrata.
7. Ce sunt supozitiile si ce importanta prezinta ele pentru logica?
8. Gasiti propozitii care sa se sprijine pe urmatoarele supozitii:
a) Sotul Mariei a fost avansat la gradul de general.
b) Nimeni nu este mai presus de lege.
c) Razboiul din Kosovo nu a adus pacea in Jugoslavia.
d) Exista zburatoare care nu sunt pasari.
9. Raspundeti prin "da" sau "nu" la urmatoarele intrebari. Argumentati apoi raspunsurile:
a) Distributivitatea termenilor depinde de valoarea logica a propozitiilor?
b) In SaS si SoS termenul S este atat distribuit cat si nedistribuit?
c) Daca non-S este distribuit intr-o propozitie, atunci S este nedistribuit?
d) Propozitiile in care distributivitatea subiectului si a predicatului este la fel sunt echivalente?
10. Care dintre propozitiile de mai jos sunt adevarate, care sunt false si de ce?
a) Nici un zeu nu este muritor.
b) Toti zeii sunt violenti.
c) Unii zei nu sunt razbunatori.
d) Numai unii zei sunt binevoitori.
e) Daca exista zei, exista si zeite.
11. Analizati structura propozitiilor de mai jos si aduceti-le la forma de exprimare standard. Reprezentati-le apoi prin diagrame Venn indicand formula corespunzatoare fiecareia[16].
Cel putin un om este incoruptibil.
Doar zburatoarele sunt inaripate.
Un numar par este de fiecare data un numar intreg.
Numai un om rau se bucura de raul altuia.
Doar tatal meu este colectionar.
Doar unii stiu sa danseze.
12) Despre ce fel de cuantor particular este vorba in propozitiile de mai jos:
1) Unii studenti nu sunt tineri,
2) Unele masini sunt furate,
3) Unele femei sunt bogate,
4) Unii logicieni nu sunt matematicieni,
5) Unii profesori sunt exigenti.
12. Demonstrati cu ajutorul diagramelor Venn ca propozitiile universal afirmative pot fi adevarate chiar daca subiectul lor este vid.
13. Indicati raporturile patratului logic dintre propozitiile de mai jos:
Unele erbivore nu sunt rumegatoare.
Nu toate erbivorele sunt rumegatoare.
Toate erbivorele sunt rumegatoare.
Nici un erbivor nu este rumegator.
Daca un animal este erbivor el este rumegator.
Exista animale care sunt erbivore si rumegatoare.
14. Se dau propozitiile p, q, r, s astfel ca intre p si q si intre r si s exista un raport de contradictie, iar intre p si r exista un raport de contrarietate. Sa se arate ce raporturi exista intre p si s, q si s, q si r.[17]
15. Completati spatiile goale din enunturile de mai jos cu unul din cuvintele "adevarat", "fals" si, respectiv, "nedecis".
Daca SaP este adevarat, atunci SeP este, SiP este , SoP este .;
Daca SiP este fals, atunci SoP este ., SeP este ., SoP este.. ;
Daca SeP este fals, atunci SiP este ., SaP este ., SoP este .;
Daca SoP este adevarat atunci SaP este ., SiP este ., SeP este ..
1 Stiind ca propozitia "Nu este posibil ~p" este adevarata, cum vor fi propozitiile:
Nu este necesar ~p,
Imposibil ~p,
Contingent p,
Non contingent ~p.
17) Explicati semnificatia cuvantului Edantuli. Aratati ce propozitii modale subordoneaza el si in ce raporturi logice stau ele cu propozitiile din Iluace.
18) Ce raporturi logice rezulta din combinarea subalternarilor Lp Mp si SeP SoP? Dar din combinarea subalternarilor Up Qp si SaP SiP? Alcatuiti octogonul logic din propozitiile astfel obtinute.
Diogenes Laertios, Despre vietile si doctrinele filosofilor, Editura Academiei RPR, Bucuresti, 1963, p. 351.
Vezi Al. Plantinga, Natura necesitatii, Editura Trei, Bucuresti, 1998 si D. Lewis, Despre pluralitatea lumilor, Tditura Tehnica, Bucuresti, 2006.
Despre circularitatile definitiilor modale am atras atentia in primul capitol cand am analizat regulile generale definitiilor.
Am in vedere sistemele standard de logica polivalenta in care operatorii logici obisnuiti ( , &, etc) sunt definiti prin tabele de adevar in maniera indicata.
Clasa C2 este corectata de Aristotel in capitolul urmator ,astfel ca, in loc de "Nu este necesar ca aceasta sa nu fie" el va lua propozitia "Nu este necesar ca aceasta sa fie". Am reprodus aceasta clasa de echivalenta tinand cond de corectia facuta de Aristotel.
Fl. Tutugan, Despre unele dificultati si confuzii in teoria logica a judecatilor modale de posibilitate, in Analele Univ. C. I. Parhon - Bucuresti, Seria St. Sociale, nr. 8, 1957.
Autorul foloseste notatii diferite insa definitiile modalitatilor si raporturile dintre ele sunt aceleasi.
Dat fiind ca Aristotel identifica posibilul cu contingentul, cele patru formule mnemotehnice apar in logica medievala in forma: Purpurea, Amabimus, Iliace si Edentuli. Repetarea aceleiasi vocale in componenta fiecarui cuvant se datoreaza faptului ca, in clasificare, posibilul nu trebuie deosebit de contingent. Daca privim cele doua modalitati ca fiind diferite, asa cum am procedat pana acum, atunci trebuie modificata si structura cuvintelor (in loc de Purpurea vom spune Purpirea etc.).
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |