METODE DE REZOLVARE A PROBLEMELOR TIPICE IN CICLUL PRIMAR
Predarea - invatarea matematicii in ciclul primar nu se poate realiza fara activitatea de rezolvare a problemelor, activitate complexa, de profunzime, in care sunt exersate la nivel superior analiza si sinteza. Activitatea de rezolvare a problemelor imbina eforturile mentale de intelegere a notiunilor invatate, a algoritmilor de calcul formati cu structurile conduitei creative si inventive.
Notiunea de problema are un continut larg de priceperi si actiuni din domenii diferite. In sens psihologic "o problema" este orice situatie, dificultate, obstacol intampinat de gandire in activitatea practica sau teoretica pentru care nu exista un raspuns gata formulat.
Activitatea de rezolvare a problemelor pune elevii in situatia de a descoperi singuri modul de rezolvare, de a emite ipoteze si a le verifica, actiuni care sporesc caracterul formativ. Rezolvarea problemelor de matematica contribuie la dezvoltarea capacitatilor creatoare ale gandirii, la sporirea flexibilitatii ei si la educarea perspicacitatii.
Rezolvarea problemelor de matematica in clasele I-IV reprezinta in esenta, rezolvarea unor situatii problematice reale pe care le putem intalni in practica, in viata. Rezolvarea problemei implica o succesiune de operatii logice, care conduc la solutii. Aceasta succesiune logica nu este altceva decat schema de rezolvare a problemei, firul de judecati oranduite logic, care alcatuiesc rationamentul problemei.
Problema de matematica reprezinta transpunerea unei situatii practice in relatii cantitative in care intervin valori numerice cunoscute si necunoscute, relatii pe baza carora se solicita determinarea valorilor necunoscute.
Scopul descoperirii implicatiei ascunse, a necunoscutei, a elaborarii rationale a solutiei, in cazul situatiilor problema, este aplicarea creatoare a cunostintelor si tehnicilor de care dispune rezolvatorul.
In cautarea caii de rezolvare a problemei se emit si se verifica o serie de ipoteze, pana se ajunge la solutia problemei care reprezinta o sinteza superioara inchiderii circuitului nervos. Schita problemei apare ca un rezultat al efortului gandirii. Procesul de rezolvare a problemelor este un proces analitico-sintetic. Analiza are un caracter general de orientare asupra continutului problemei.
Cautarea unor procedee de analiza si sinteza cat mai eficiente, pentru a conduce gandirea elevului pe cai cat mai scurte si mai sigure catre aflarea necunoscutei, constituie una din sarcinile de baza ce-i revin invatatorului.
Problema impune in rezolvarea ei o activitate de descoperire. Textul problemei indica datele, conditia problemei (relatiile dintre date si necunoscuta) si intrebarea problemei.
Varietatea si complexitatea problemelor pe care le rezolva elevii sporeste efortul mental si eficienta formativa a activitatii de rezolvare a problemelor. In rezolvarea problemelor intervine o serie de tehnici, procedee, modul de actiune, de deprinderi si activitati de munca intelectuala.
In activitatea de rezolvare a unei probleme se parcurg mai multe etape. In fiecare etapa are loc un proces de reorganizare a datelor si de reformulare a problemei, pe baza activitatii de orientare a rezolvatorului pe drumul si in directia solutiei problemei.
In rezolvarea problemelor de o mare importanta este intelegerea structurii si a logicii rezolvarii ei. Elevul trebuie sa cuprinda in sfera gandirii sale intregul "film" al desfasurarii rationamentului si sa-l retina drept element esential. Pentru generalizarea rationamentului, elevii trebuie sa aiba formate capacitatile si de a intelege datele problemei, de a sesiza conditia problemei si de a orienta logic sirul de judecari catre intrebarea problemei.
Pentru rezolvarea corecta a problemei trebuie sa parcurgem urmatoarele etape:
I. Cunoasterea enuntului problemei
Aceasta etapa de inceput presupune citirea enuntului problemei, de
catre institutor sau elevi de mai multe ori, pana la insusirea corecta. Se pun in evidenta datele si legaturile dintre ele, se scriu pe tabla si in caiet. Elevul care rezolva problema trebuie sa identifice cerinta problemei, adica elementul necunoscut.
II. Intelegerea enuntului problemei
Deoarece enuntul problemei contine un minim de informatii, el trebuie
optimizat prin delimitarea datelor, prin evidentierea relatiilor dintre ele si stabilirea intrebarii problemei. Aceasta optimizare se realizeaza prin discutii cu elevii. In acest sens se pot folosi si alte mijloace: ilustrarea prin imagini, scheme, grafice, etc.
Intelegerea enuntului permite generalizarea si abstractizarea prin construirea unei scheme care contine esentialul, eliminand aspectele descriptive.
III. Analiza problemei si intocmirea planului de rezolvare
In aceasta etapa se descopera calea de rezolvare a problemei,
eliminandu-se elementele nesemnificative si se elaboreaza planul logic de rezolvare. Astfel cel care rezolva problema efectueaza un sir de rationamente care vor duce la alcatuirea problemei simple prin a caror rezolvare se ajunge la raspuns. Examinarea problemei se face prin cele doua metode generale, metoda analitica si metoda sintetica.
IV. Alegerea si efectuarea operatiilor corespunzatoare
succesiunii planului de rezolvare
Din planul de rezolvare elevii aleg si efectueaza calculele constientizand semnificatia fiecarui calcul oral sau scris si realizeaza conexiunile necesare pentru obtinerea rezultatului final. Se va acorda o importanta deosebita redactarii planului de rezolvare, consemnand judecatile intelegand corect unitatile de masura si finalizand cu scrierea rezultatului.
V. Activitati suplimentare
In aceasta etapa se pot concretiza urmatoarele:
verificarea solutiei problemei;
scrierea problemei sub forma de exercitiu;
depistarea altor variante de rezolvare;
generalizare;
compunere de probleme.
Chiar daca aceasta etapa este facultativa pentru formarea priceperilor
si a deprinderilor corecte de rezolvare a unei probleme este necesara verificarea solutiei deoarece astfel se realizeaza autocontrolul asupra corectitudinii demersului de rezolvare. Aceasta etapa poate fi valorificata de institutor in directia cultivarii creativitatii elevilor si a cresterii interesului pentru matematica.
2. METODE GENERALE DE REZOLVARE A PROBLEMELOR DE ARITMETICA
Modul de prezentare si solutionare a problemelor se va face prin respectarea particularitatilor de varsta de la concret-intuitiv (cum ar fi manipularea obiectelor, a instrumentelor de masura: balantele, metrul, banii, etc. ; decupaje si asamblari de figuri geometrice; experimente asupra unor masuratori, cantariri etc.), la reprezentare grafica imagistica (probleme pe baza unor imagini cu concretizarea relatiilor intre marimi prin segmente, diagrame, sageti etc.), la descompunerea problemelor compuse in probleme simple, fara a fi rezolvate succesiv, deoarece nu acest fapt intereseaza, ci construirea rationamentului, legatura dintre secvente.
In cadrul acestor activitati, elevii sunt dirijati sa sesizeze mersul rationamentului si sa invete sa elaboreze tactica si strategia solutionarii prin elaborarea planului de rezolvare a problemei.
Examinarea unei probleme compuse se realizeaza, de obicei, prin metodele analitica, sintetica sau folosite simultan.
Deosebirea dintre ele consta, practic, in punctul de plecare al rationamentului. Prin metoda sintezei se porneste de la datele problemei spre aflarea solutiei, iar prin metoda analizei se pleaca de la intrebarea problemei spre aflarea solutiei, iar prin metoda analizei se pleaca de la intrebarea problemei spre datele ei si stabilirea relatiilor matematice dintre acestea.
Practica a demonstrat ca metoda sintezei este mai accesibila, dar nu solicita prea mult gandirea elevilor, uneori abatandu-le atentia de la intrebarea problemei.
Metoda analitica pare mai dificila, dar solicita mai mult gandirea elevilor, determinandu-i sa priveasca problema in totalitatea ei.
Analiza logica a problemei, dupa repetarea si intelegerea enuntului, se realizeaza concomitent cu formularea orala a planului de rezolvare, urmate de consemnarea in scris a acestuia prin activitate frontala sau independenta, sub variate forme: de intrebari, titluri, enunturi succinte etc.
Rezolvarea poate fi scrisa prin intercalarea intrebarilor din plan cu calculul, asigurand o estetica a asezarii in pagina, care ilustreaza legatura intre consemnarea succinta a datelor enuntului, a planului gandit si a calculului realizat, cu marcarea raspunsului obtinut si generalizarea prin transpunerea problemei in expresie numerica sau formula literala.
Este oportun sa se rezolve nu mai mult de una-doua probleme intr-o ora de curs, insistand asupra rationamentului si investigand solutionarea pe mai multe cai, pentru exersarea flexibilitatii gandirii decat sa se exagereze cu solutionarea stereotipa, superficiala a mai multor probleme sau sa se consume timpul pentru o singura problema.
Locul problemei in succesiunea secventelor instruirii trebuie bine ales, in functie de curba de efort la care este solicitat copilul si obiectivele stabilite.
Oricum sugerez sa se evite situatiile in care problemele sunt planificate exclusiv la sfarsitul lectiei, lasand sarcina efectuarii lor complete in recreatie sau acasa.
Procesul de gandire care are loc in scopul precizarii problemelor simple ce alcatuiesc o problema compusa si a succesiunii lor, astfel incat intrebarea ultimei probleme simple sa coincida cu intrebarea finala a problemei date se numeste examinare sau analiza a problemei.
METODA ANALITICA
Folosirea metodei analitice presupune plecarea de la intrebarea problemei, descompunerea ei in probleme simple, organizate intr-o succesiune logica si rezolvarea acestora sa conduca in mod deductiv de la valoarea necunoscuta catre valorile cunoscute la formularea raspunsului cerut de problema.
Pentru a vedea cum folosim aceste metode vom pleca de la examinarea urmatoarei probleme:
. La o ferma viticola lucreaza doua echipe: prima are 10 muncitori care culeg zilnic cate 240 kg de struguri si a doua formata din 12 muncitori care culeg zilnic cate 220 kg de struguri fiecare. Stiind ca pretul unui kg de struguri este de 8000 lei, sa se afle valoarea totala realizata intr-o zi de cele doua echipe.
Examinarea problemei:
Plecand de la intrebarea problemei pentru aflarea valorii totale, trebuie sa cunoastem cantitatea totala de struguri culeasa de cele doua echipe.
Aceasta cantitate se poate afla cunoscand cantitatea de struguri culeasa de prima echipa si cantitatea culeasa de a doua echipa.
Schematic, va arata astfel:
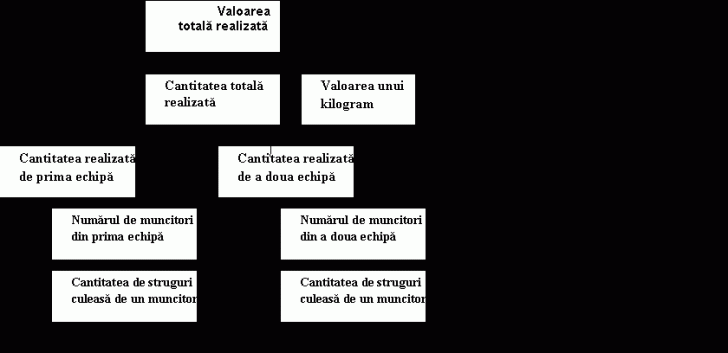
Cu aceasta schema vom transpune enuntarea problemelor simple in care s-a descompus problema, sub forma unui plan de rezolvare:
Care este cantitatea de struguri culeasa de prima echipa ?
240 kg x 10 = 2400 kg
Care este cantitatea de struguri culeasa de a doua echipa?
220 kg x 12 = 2640 kg
Care este cantitatea de struguri culeasa de cele doua echipe?
2400 kg + 2640 kg = 5040 kg
Care este valoarea totala realizata de cele doua echipe?
8000 lei x 5040 = 40320000 lei.
METODA SINTETICA
Folosirea metodei sintetice presupune elaborarea unor rationamente care grupeaza datele dupa relatiile dintre ele, formularea unor probleme simple si asezarea lor intr-o succesiune logica a caror rezolvare sa se incheie cu acea problema simpla, a carei intrebare sa coincida cu intrebarea problemei.
Planul de rezolvare coincide cu cel realizat la metoda analitica.
Cele doua metode generale de examinare, avand la baza cele doua operatii ale gandirii se gasesc intr-o stransa conexiune cauzata de cele doua procedee: analitic si sintetic, care se conditioneaza reciproc.
Din acest motiv utilizarea acestor doua metode nu poate fi separata total, ci putem avea in anumite momente o tenta dominanta a unei dintre ele, dar in examinarea unei probleme intervin ambele operatii ale procesului de gandire.
Intr-o problema compusa, descompunerea ei in probleme simple presupune un proces de analiza, iar formularea planului de rezolvare si a succesiunii logice presupune un proces de sinteza.
Acestea fac ca cele doua metode sa apara sub denumirea de "metoda analitica si sintetica".
Schematic, examinarea problemei prin metoda sintetica se poate expune astfel:
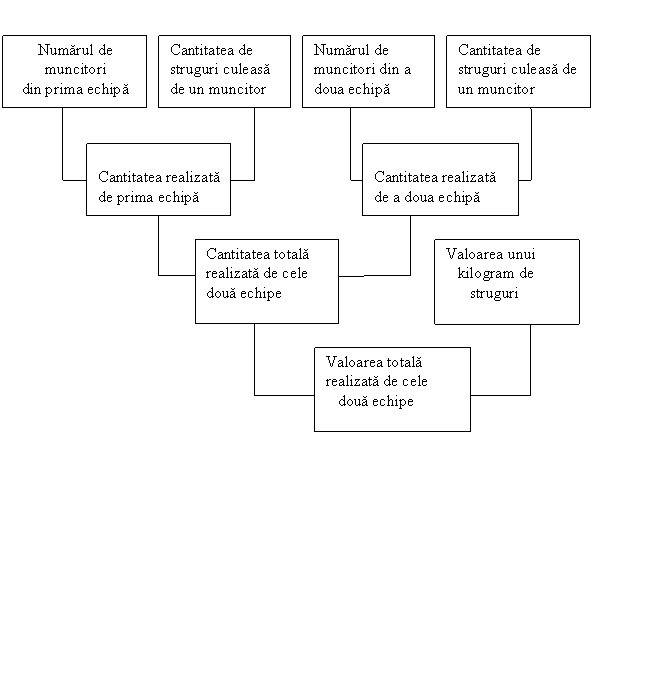
3. METODE DE REZOLVARE A PROBLEMELOR TIPICE
3.1. Probleme de aflare a doua numere cunoscand: suma si diferenta
lor, suma si raportul lor, diferenta si raportul lor
a) Probleme de aflare a doua numere cunoscand suma si diferenta lor
a + b = s
a - b = d.
Sa se afle numerele a si b.
Rezolvare: Adunand cele doua egalitati, se obtine:
2a = s + d, de unde a = s + d .
2
Scazand cele doua egalitati, se obtine:
2b = s - d, de unde b = s - d .
2
Exemplu
numeric: a + b = 1 634,
a - b = 884.
2a = 1 634 + 884 → a = 1 634 + 884 = 2 518 = 1 259;
2 2
2b = 1 634 - 884 → b = 1 634 - 884 = 750 = 375.
2 2
In mod intuitiv, rezolvarea tipului de probleme in care se cere aflarea a doua numere cand se cunoaste suma si diferenta lor se poate face prin metoda grafica sau figurativa.
Utilizand aceasta metoda se considera un segment de dreapta AB care reprezinta numarul mai mare a si un alt segment de dreapta CD care reprezinta numarul mai mic b.
A a B
E a - b = d a + b = s
C b -
----- ----- ----- F
D
Se observa ca daca din segmentul AB se inlatura portiunea EB, care reprezinta diferenta celor doua segmente, se obtine segmentul AE egal cu CD, adica daca din suma celor doua segmente AB si CD se scade diferenta lor EB se obtine dublul segmentului mai mic CD.
Iar daca la segmentul mai mic CD se adauga portiunea DF astfel ca segmentul CF obtinut sa fie egal cu segmentul AB, atunci segmentele AB si
CF, luate impreuna, reprezinta suma numerelor date, adunata cu diferenta lor, care, evident, este egala cu dublul segmentului mai mare AB.
de legume, altele de carne. Stiind ca numarul cutiilor de conserve de legume este cu 140 mai mare decat al celor de carne, sa se afle cate cutii de conserve au fost de fiecare fel.
Rezolvare:
a = numarul cutiilor de conserve de legume
b = numarul cutiilor de conserve de carne, a > b
atunci: a + b = 640, a - b = 140.
Metoda I: a = s + d , adica a = 640 + 140 = 780 = 390.
2 2 2
b = s - d, adica b = 640 - 140 = 500 = 250.
2 2 2
Deci s-au adus 390 conserve de legume si 250 conserve de carne.
Metoda II - figurativa
2a = a + b + 140 = 640 + 140 = 780
de unde a = 780 = 390.
2
A a B
E 140
C b -
----- ----- ----- F
D 140
2b = a + b - 140 = 640 - 140 = 500,
de unde b = 500 = 250.
2
Explicatii: Daca din numarul a se scade diferenta de 140, el ramane egal cu b, deci
2b = a + b - 140, adica 2b = s - d si b = s - d .
2
Daca la numarul b se adauga diferenta de 140, el devine egal cu numarul a, astfel incat
2a = a + b + 140, adica 2a = s + d si a = s + d.
2
In doua magazii sunt depozitate 7 867 kg zahar. Dupa ce din prima magazie se transporta in cealalta 1 703 kg, in a doua magazie sunt cu 315 kg mai mult zahar decat in prima.
Cate kilograme de zahar au fost depozitate, la inceput, in fiecare magazie?
Rezolvare:
Metoda I. Consideram a, respectiv b cantitatile initiale. Atunci, judecand ca la problema precedenta, avem:
a + b = 7 867 a = 5
479
a - 1 703 = b + 1 703 - 315 → b = 2 388
Metoda II. Consideram a', b' cantitatile finale, unde a' s-a obtinut micsorand cantitatea initiala a cu 1 703 kg, iar b' s-a obtinut marind cantitatea initiala b cu 1
703 kg, b' devenind astfel mai mare decat a' cu 315 kg, adica:
a' + b' = 7 867 a' = 3 776,
b' - a' = 315 b' = 4 091.
Presupunand ca se renunta la transferul cantitatilor, atunci in prima magazie se readuce cantitatea de 1703 kg zahar din magazia a doua, ajungandu-se astfel la cantitatile initiale, adica:
a = a' + 1 703 = 3 776 + 1 703 = 5 479
b = b' - 1 703 = 4 091 - 1 703 = 2 388.
4. La inceputul anului scolar, o librarie a distribuit celor 3 licee din oras in total 13 848 manuale. Al doilea liceu a primit cu 1 794 manuale mai putin decat primul, iar al treilea liceu cu 282 manuale mai mult decat al doilea.
Cate manuale a primit fiecare liceu?
Rezolvare: Prin metoda figurativa:
A B
a
- b = 1 794
C b D----- ----- ----------------
E c F----- ----- ---------
c - b = 282
Daca numarul a, care reprezinta manualele primite de primul liceu se micsoreaza cu 1 794, el devine egal cu b (numarul de manuale distribuite liceului al doilea), a - 1 794 = b.
Daca din c (numarul manualelor distribuite liceului al treilea) se scad cele 282 manuale (cu cat c este mai mare decat b), atunci c - 282 = b si prin urmare relatia a + b + c = 13 848 devine:
(a - 1 794) + b + (c - 282) = 13 848 - 1 794 - 282.
b + b + b = 11 772,
3b = 11 772 → b = 11 772 = 3 924,
3
apoi: a = b + 1 794 = 3 924 + 1 794 = 5 718,
c = b + 282 = 3 924 + 282 = 4 206.
In mod analog se pot completa cantitatile b si c cu diferentele respective, astfel ca sa devina egale cu a.
Rezolvare prin suma si diferenta:
a + b + c = 13 848,
a - b = 1 794,
c - b = 282 → c = 282 + b;
atunci a + b + b + 282 = 13 848 sau a + 2b = 13 848 - 282 = 13 566.
Utilizand
relatiile: a + 2b = 13 566,
a - b = 1 794
si scazandu-le, obtinem:
3b = 11 772 → b = 3 924,
c = b + 282 = 3 924 + 282 = 4 206,
a = 13 848 - (b + c) = 13 848 - (3 924 + 4 206) = 5 718.
5. In doua magazii se gaseste cantitatea de 1 380 q grau. Daca din prima magazie se transporta in a doua 219 q, atunci cantitatile de grau din cele doua magazii devin egale.
Ce cantitati de grau s-au aflat initial in fiecare magazie?
Raspuns: 909 kg; 471 kg.
6. Trei lingouri de fonta cantaresc in total 245 kg. Al doilea lingou are masa cu 42 kg mai mica decat primul si cu 25 kg mai mare decat al treilea. Sa se afle masa fiecarui lingou.
Raspuns: 118 kg; 76 kg; 51 kg.
b) Probleme de aflare a doua numere cunoscand suma si raportul lor
1. Se considera doua numere a, b cunoscand suma lor a + b = s si raportul lor a = m .
b n
Raportul a = m are urmatoarea interpretare:
b n
* numarului a ii corespund m parti din suma a + b = s;
* numarului b ii corespund n parti din suma a + b = s.
Cu alte cuvinte, suma a + b este formata din m + n parti.
Daca suma a +b = s a celor doua numere se imparte la numarul total m + n
al partilor, se pot afla apoi m sau n parti, adica:
(a + b) : (m + n) = p (p = marimea unei parti)
de unde a = p . m
b = p . n.
Observatie: Problemele de aceasta categorie se pot rezolva si prin propozitii derivate.
2. Doi inovatori au fost premiati
cu suma de 5 875 000 lei. Stiind ca sumele ce li se cuvin sunt in
raportul 
, sa se afle ce suma a primit fiecare inovator.
Rezolvare:
a = suma cuvenita primului inovator
b =
suma cuvenita celui de-al doilea inovator
a + b = 5 875 000
atunci 
=
deci a → 2 parti, b → 3 parti, a + b →2 + 3 = 5 parti.
O singura parte este egala cu: 5 875 000 : 5 = 1 175 000
de unde: 2 parti fac 1 175 000 * 2 = 2 350 000
3 parti fac 1 175 000 * 3 = 3 525 000
deci: a = 2 350 000 (lei),
b = 3 525 000 (lei).
3. Un muncitor avea doua librete de economii in valoare totala de
5 000 000 lei. Dupa ce de pe primul libret a scos
527 000 lei, iar de pe al doilea 545 000 lei, i-a ramas pe primul libret o
suma egala cu 
din suma
ramasa pe al doilea libret.
Care au fost sumele initiale?
Rezolvare:
Se noteaza cu a, b sumele initiale si cu a', b' sumele ramase respectiv pe primul si al doilea libret.
Atunci avem:
a' + b' = 5 000 000 - (527 000 + 545 000) = 5 000 000 - 1 072 000 = 3 928 000
a' = 3 b' sau a' = 3 → a'→ 3
5 b' 5 b'→ 5 parti
adica: a' = 3 928 000 : 8 * 3 = 491 000 * 3 = 1 473 000
b' =3 928 000 : 8 * 5 = 491 000 * 5 = 2 455 000
iar: a = 1 473 000 + 527 000 = 2 000 000 (lei pe primul libret),
b = 2 455 000 + 545 000 = 3 000 000 (lei pe al doilea libret).
4. Doi inovatori au fost premiati cu suma de 2 892 000 lei, celui de-al doilea revenindu-i 5/7 din suma cuvenita celui dintai.
Ce suma a primit fiecare inovator?
Raspuns: 1 687 000 lei; 1 205 000 lei.
5. Un turist a parcurs un drum in lungime de 475 km, o parte pe jos, o parte cu bicicleta.
Partea din drum parcursa pe jos reprezinta 2/17 din cea parcursa cu bicicleta.
Cati kilometri a parcurs pe jos si cati cu bicicleta?
Raspuns: 50 km; 425 km.
c) Probleme de aflare a doua numere cunoscand diferenta si raportul lor
1. Se considera doua numere a, b unde a > b, cunoscand diferenta lor
a - b = d si
raportul lor = 
.
Dand raportului m/n aceeasi interpretare ca in cazul precedent, adica numarului a ii corespund m parti si numarului b ii corespund n parti de acelasi fel din suma celor doua numere, rezulta ca suma a + b este formata din m + n parti, iar diferenta a - b este formata din m - n parti; atunci o singura parte va fi egala cu catul dintre diferenta numerelor si diferenta partilor, adica:
(a - b) : (m - n) = p (p = marimea unei singure parti)
de unde: a = p ∙ m
b = p ∙ n.
Observatie: Problemele de aceasta categorie se pot rezolva si prin proportii derivate.
2. Doua echipe de elevi
practicanti, de la o scoala agricola, au cules rosii.
Prima echipa a cules cu 2 359,2 kg mai putin decat a doua, iar
cantitatile stranse de cele doua echipe sunt in raportul 
.
Ce cantitate de rosii au cules cele doua echipe impreuna?
Rezolvare:
a = cantitatea de rosii culese de prima echipa
b = cantitatea de rosii culese de a doua echipa, a < b
b - a = 2 359,2
deci: a = 9 a → 9 parti
b 13 → b →13 parti →(b - a) → 4 parti
deci diferenta de 2 359,2 reprezinta 4 parti, de unde o singura parte este egala cu: 2 359,2 : 4 = 589,8
dar 9 parti fac 589,8 ∙ 9 = 5 308,2 deci a = 5 308,2 kg
13 parti fac 589,8 ∙ 13 = 7 667,4 deci b = 7 667,4 kg.
Cele doua echipe au cules 12 975,6 kg rosii.
3. Un incubator a scos in prima serie, seria de proba, un numar de pui. In a doua serie a scos de 26 ori mai multi pui fata de prima serie, iar in seria a treia de 43 ori mai multi pui decat in prima serie. Stiind ca numarul puilor scosi in a doua serie este cu 35 700 mai mic decat numarul puilor scosi in seria a treia, sa se afle cati pui a scos incubatorul in fiecare din cele trei serii si cati in total.
Rezolvare:
a = numarul puilor scosi in seria I
b = numarul puilor scosi in seria a II-a
c = numarul puilor scosi in seria a III-a
Din datele problemei rezulta:
c - b =
35 700; 
= 
.
Deci numarului b ii corespund 26 parti, numarului c ii corespund 43 parti, iar diferentei c - b ii corespund 43 - 26 parti.
Dar diferenta c - b este egala cu 35 700, deci acestei diferente, care este formata din 17 parti, ii corespunde numarul 35 700, de unde urmeaza ca o singura parte este egala cu
35 700 : 17 = 2 100, iar 26 parti 2 100 ∙ 26 = 54 600 si 43 parti 2 100 ∙ 43 = 90 300.
Rezulta ca incubatorul a scos:
- in prima serie 2 100 pui,
- in a doua serie 56 600 pui,
- in a treia serie 90 300 pui,
in total 147 000 pui.
4. Intr-o magazie era de 5 ori mai multa faina decat in alta. Daca din prima magazie se scoate cantitatea de 1000 kg faina, iar in cea de-a doua se depoziteaza inca 448 kg faina, atunci cantitatile de faina din cele doua magazii devin egale.
Ce cantitati de faina erau la inceput in cele doua magazii?
Rezolvare:
a = cantitatea de faina aflata initial in prima magazie,
b = cantitatea de faina aflata initial in a doua magazie
iar
= 
sau 
= 
.
Urmeaza sa stabilim diferenta cantitatilor si in acest scop utilizam metoda
grafica:
A a -------- ----- ------ B
E 1 000 kg
C b ----- ----- -------
D 448 kg F
Comparand segmentele AB si CD, care reprezinta respectiv cantitatile a si b, se observa ca diferenta AB - CD este egala cu 1000 + 448, deci
a - b = 1 448.
Deci: - numarului a ii corespund 5 parti;
numarului b ii corespunde 1 parte;
diferentei a - b ii corespund 5 - 1 = 4 parti
adica numarul 1 448 este format din 4 parti, o parte fiind egala cu
1 448 : 4= 362, de unde a = 362 ∙ 5 = 1 810
b = 362 ∙ 1 = 362.
Deci in prima magazie au fost 1 810 kg faina, iar in a doua magazie au fost 362 kg faina.
Verificare: 1 810 - 1 000 = 810,
362 + 448 = 810.
5. La doua tonete s-au vandut legume si fructe. Vanzatorul de la prima toneta a incasat cu 3 400 000 lei mai putin decat cel de la a doua toneta.
Ce suma a realizat fiecare vanzator daca suma incasata de al doilea este de 3 ori mai mare decat cea incasata de primul?
Raspuns: 1 700 000 lei; 5 100 000 lei.
3.2. PROBLEME DE MISCARE
Problemele de miscare sunt acelea in care se afla una dintre
marimile: spatiul (distanta), viteza sau timpul, cand se cunosc doua dintre ele sau diferite relatii intre acestea.
In general, in problemele de miscare se va vorbi despre miscarea uniforma a unui mobil, adica, in intervale de timp egale mobilul parcurge distante (spatii) egale.
In acest caz, cele trei marimi s, v si t sunt legate prin relatia:
s = v · t
Iar din aceasta calculam un factor (v, respectiv t) din faptul ca se cunoaste produsul (s) si celalalt factor (t, respectiv v ).
t = s/v
v = s/t
si
La rezolvarea problemelor de miscare se pot folosi atat metodele aritmetice generale si speciale, cat si cele algebrice. Aceasta ne-ar permite sa facem o clasificare a problemelor de miscare dupa metoda aritmetica de rezolvare a lor. Dar, uneori, aceste metode se interfereaza, de aceea vom prefera o alta clasificare a problemelor de acest tip.
a. Probleme ce conduc direct la aflarea spatiului, vitezei sau timpului.
. Doi turisti parcurg distanta de la A la B. Primul turist a sosit in B cu doua ore mai tarziu decat al doilea. Viteza primului turist este de 4 km/h, iar a celui de-al doilea de 6 km/h.
Sa se determine distanta de la A la B.
Rezolvarea I: (aritmetica)
In fiecare ora, primul turist ramane in urma celui de-al doilea cu 2 km. Pana ce al doilea turist a ajuns in B, primul a ramas in urma cu o distanta pe care a facut-o in doua ore, adica s = 4 km/h · 2 h = 8 km. Aceasta ramanere in urma s-a realizat intr-un timp t = 8 km : 2 km/h = 4 h.
Deci, al doilea turist a mers o distanta s = 6 km/h · 4 h = 24 km = AB.
Rezolvarea II: (algebrica)
Primul turist parcurge distanta
AB = s in timpul t1 = 
, iar al doilea in timpul t2 = 
.
Dar, diferenta dintre acesti timpi este de 2 ore, deci avem ecuatia:
- = 2 ↔ 3s - 2s = 24 ↔ s = 24;
deci AB = s = 24 km.
La ce ora trebuie sa plece la gara o persoana ce poate strabate 4 km/h ca sa ia trenul de 8 h 05 min, daca gara se afla la o distanta de 4,5 km si pentru cumpararea biletului ii mai trebuie 10 minute.
Raspuns: 6 h 47 min 30 s.
3. Un tren de marfa, mergand cu aceeasi viteza, parcurge distanta de la A la B de 238 km in 7 ore. Dupa doua ore de la plecarea trenului din A pleaca dupa el un alt tren.
Cu ce viteza trebuie sa mearga trenul al doilea ca sa-l ajunga pe primul intr- o statie intermediara care se afla la o distanta de 136 km fata de statia A?
Raspuns: 68 km/h.
b. Probleme de intalnire a mobilelor, cand deplasarea se face in sensuri opuse
Un pieton, care parcurge 5 km pe ora, pleaca din orasul A spre orasul B. In acelasi moment, un biciclist pleaca din B spre A, cu viteza de 22 km/h. Intre orase este o distanta de 81 km.
Dupa cat timp se intalneste pietonul cu biciclistul? La ce distanta de orasul B se intalnesc?
Rezolvarea I: (aritmetica)
In fiecare ora, distanta dintre pieton si biciclist se micsoreaza cu
5 km + 22 km = 27 km. Pentru ca ei sa se intalneasca, trebuie sa treaca atatea ore de cate ori se cuprind 27 km in 81 km,adica 81 km :27 km/h=3 h.
Se intalnesc la distanta BI = 22 km/h · 3 h = 66 km de orasul B.
81 km
A ..t B
0h 5 km/h 22 km/h 0 h
Observatie: Cand distanta dintre punctele de plecare este s, iar mobilele pleaca in acelasi moment si merg unul catre celalalt cu vitezele v1 si v2, atunci timpul dupa care se intalnesc este dat de formula:
t = s : (v1
+ v2)
Rezolvarea II: (aritmetica)
Fie I punctul de intalnire. Pietonul parcurge drumul AI, iar biciclistul BI. Aceste drumuri sunt proportionale cu vitezele, deci avem: AI = BI sau,
5 22
schimband locul mezilor: AI = 5, iar AI + BI = 81, deci problema s-a redus
BI 22
la una tipica: de aflare a doua numere cand cunoastem suma si raportul lor.
Derivand o noua proportie din cea obtinuta, avem:
AI + BI = 5 + 22 ; 81 = 27 → BI = 22 · 81 = 66 (km);
BI 22 BI 22 27
AI = 81 - 66 = 15 (km).
Pietonul si biciclistul se intalnesc dupa 66 km: 22 km/h = 3 h (sau 15 km : 5 km/h = 3 h).
Rezolvarea III: (algebrica)
Notam t = numarul de ore scurse pana la intalnire, atunci avem ecuatia:
5t + 22t = 81 ↔ 27t = 81 ↔ t = 3.
Deci intalnirea are loc dupa 3 h, la 22 km/h · 3 h = 66 km fata de orasul B.
2. La 12 h 35 min pleaca un tren din Bacau spre Bucuresti, cu viteza de 60 km/h, iar la 12 h 50 min pleaca din Bucuresti spre Bacau un alt tren, cu viteza de 90 km/h. Distanta dintre garile Bacau si Bucuresti este de 315 km.
La ce ora si la ce distanta fata de punctele lor de plecare se intalnesc cele doua trenuri?
Raspuns: 14 h 50 min; la 135 km de Bacau si la 180 km de Bucuresti.
c. Probleme de intalnire a mobilelor cand deplasarea se face in acelasi sens
1. Un biciclist, avand viteza de 24 km/h, pleaca din orasul A. Dupa trei ore pleaca tot din A, in aceeasi directie, un motociclist, avand viteza de 42 km/h.
Rezolvare: (aritmetica)
Avansul biciclistului (distanta parcursa in trei ore) este AB = 24km ·3=72 km
Motociclistul castiga in fiecare ora 42 km - 24 km = 18 km.
72 km
A B I
3 h
24 km
3h 42 km
Pentru a castiga 72 km, motociclistul merge un timp de 72 km : 18 km/h =
= 4 h, acesta fiind si timpul dupa care l-a ajuns pe biciclist, iar distanta de la orasul A este, la intalnire, AI = 42 km · 4 = 168 km.
t = s : (v1
- v2); v1 > v2.
Observatie: Cand distanta
dintre punctele de plecare este s, iar mobilele pornesc in acelasi timp
si merg in acelasi sens cu vitezele v1 si v2,
atunci timpul necesar primului mobil ca sa-l ajunga pe al doilea este
dat de formula:
Rezolvarea II: (aritmetica)
Fie I punctul in care motociclistul il ajunge pe biciclist. In timp ce motociclistul face drumul AI, biciclistul face drumul BI. Aceste drumuri sunt
proportionale cu vitezele, deci avem AI = BI sau, schimband locul mezilor:
AI = 42, iar AI - BI = 24 · 3 = 72, deci problema s-a redus la una tipica: de
BI 24
Aflare a doua numere cand cunoastem diferenta si raportul lor. Derivand o noua proportie din cea obtinuta avem:
AI - BI = 42 - 24; 72 = 18 → BI = 72 ·24 = 96 (km);
BI 24 BI 24 18
AI = 72 km + 96 km = 168 km.
Biciclistul si motociclistul se intalnesc dupa 26 km : 24 km/h = 4 h sau
168 km : 42 km/h = 4 h, de la plecarea motociclistului.
Rezolvarea III: (algebrica)
Notam cu t numarul de ore scurse pana la intalnire si atunci avem ecuatia:
42t -24t = 24 · 3 ↔ 18 t = 72 ↔ t = 4 h.
Motociclistul l-a ajuns pe biciclist la distanta de 42 km · 4 = 168 km de orasul A.
2. Un turist a plecat din localitatea A spre localitatea B la ora 6 si a parcurs in medie 4,8 km/h. Dupa 5 h 45 min a pornit dupa el din A un biciclist care a parcurs in fiecare 15 minute 3,5 km.
Cand a ajuns biciclistul pe turist si la ce distanta de B, daca distanta dintre cele doua localitati este de 85 km?
Raspuns: La 14 h 45 min, la distanta de 43 km de B.
d. Probleme cu compunerea vitezelor
O barca cu motor, mergand in sensul apei, strabate distanta dintre doua porturi in 13½ ore, iar in contra apei in 18 ore. Sa se afle in cate ore va strabate aceeasi distanta o luntre care ar fi luata numai de curentul apei.
Rezolvarea I: (aritmetica)
Notam cu v1 viteza barcii cu motor pe o apa statatoare si cu v2 viteza cursului de apa (care coincide cu cea a luntrei). Viteza cu care barca merge in sensul apei este v1 + v2, iar cea cu care merge impotriva apei este v1 - v2. Pe o anumita distanta, vitezele sunt invers proportionale cu timpii de mers, adica:
v1 + v2 = v1 - v2 , v1 + v2 = 18 = 36 = 4 .
1 : 13
1 : 18 v1 - v2 13 27 3
Din proportia obtinuta derivam alta:
(v1 + v2) +(v1 - v2) = 4 + 3 , v1 = 7
(v1 + v2) - (v1 - v2) 4 - 3 v2 1
adica, viteza barcii cu motor este de 7 ori mai mare decat viteza cursului apei
(v1 = 7 v2).
Daca notam cu d distanta dintre porturi, timpul in care aceasta este strabatuta impotriva apei este d : (v1 - v2) = d : (7v2 - v2) = d : 6v2, iar cel in care luntrea este dusa de curent este d : v2. Dar impotriva curentului apei barca face 18 ore, deci d : 6v2 = 18 ore, si atunci timpul in care luntrea parcurge distanta d este:
t = d : v2 = d: (6v2 : 6) = 18 ·6 = 108 (ore).
Rezolvarea II: (aritmetica)
Consideram
distanta dintre cele doua porturi un intreg. Drumul parcurs de
barca cu motor in sensul apei intr-o ora va fi: 1 : 13 = 
, iar contra apei 
.
Pastram aceleasi notatii v1 si v2, ca si la "rezolvarea I".
Cand barca merge in sensul apei, drumul pe care-l face intr-o ora este
v1 + v2 , iar cand merge impotriva apei v1 - v2 , deci:
- 
= (v1 + v2) - (v1 - v2)
↔ 
= 2v2 ↔ 
= 2v2 ↔ v2 = : 2 = 
din distanta pe
ora, adica luntrea parcurge toata distanta in 108 ore.
Rezolvarea III: (algebrica)
Pastram aceleasi notatii v1 si v2, ca si la "rezolvarea I", si notam cu d distanta dintre cele doua porturi.
Atunci avem sistemul de ecuatii:
v1
+ v2 = s : 13 ,
v1 - v2 = s : 18.
Prin scaderea ecuatiilor, parte cu parte,
obtinem v2 = 
, adica luntrea
parcurge distanta in 108 ore.
. Un calator care mergea intr-un tren de persoane ce avea viteza de 70 km/h, a observat ca un tren accelerat care mergea in sens contrar a trecut pe langa el in trei secunde.
Sa se afle viteza trenului accelerat, stiind ca lungimea lui este de 150 m.
Rezolvare:
Viteza personalului este v1 = 70 km/h.
Viteza aparenta a acceleratului este:
v2
= 
= 
= 50 m/s = 
= 180 (km/h).
Viteza reala a acceleratului este:
v = v2 - v1 = 180 km/h - 70 km/h = 110 km/h.
. Pe o linie dubla de cale ferata, un tren accelerat lung de 60 m
depaseste un tren de persoane lung de 80 m, care merge in acelasi sens, in 28 de secunde. Acelasi tren accelerat intalneste la intoarcere trenul de persoane,
pe langa care trece in 4 secunde.
Care sunt vitezele celor doua trenuri?
Indicatie si raspuns: Mergand in acelasi sens, trenurile trec unul pe langa celalalt cu o viteza egala cu diferenta vitezelor lor, iar in sensuri contrarii cu o viteza egala cu suma vitezelor.
Se gaseste ca viteza acceleratului este 20 m/s sau 72 km/h, iar a personalului de 15 m/s sau 54 km/h.
e. Probleme de miscare care se rezolva prin metoda falsei ipoteze
1. Un pieton a parcurs distanta, dus intors, dintre doua localitati, in 9 ore; la dus cu viteza de 4 km/h, iar la intors cu viteza de 5 m/h.
Sa se afle distanta dintre cele doua localitati.
Rezolvarea I: (aritmetica)
Presupunem ca distanta dintre cele doua localitati este de 60 km.
Timpul la dus va fi t1 = 60 km : 4 km/h = 15 h.
Timpul la intors va fi t2 = 60 km : 5 km/h = 12 h.
Timpul total (dus si intors) va fi t = 12 h + 15 h = 27 h.
Dar, in realitate, timpul este mai mic decat cel din falsa ipoteza de 27h : 9h =3 ori.
Daca timpul real este de 3 ori mai mic, atunci si drumul va fi de 3 ori mai mic (spatiul si timpul sunt marimi direct proportionale, in cazul vitezei constante).
Deci drumul real dintre cele doua localitati este de 60 km : 3 = 20 km.
Rezolvarea II: (aritmetica)
Pietonul
parcurge 1 km la dus in 
ore, iar la intoarcere
in ore. Un kilometru,
dus-intors, il strabate in ore + ore = 
ore. Deci
distanta dintre cele doua localitati este de 9 : = 20 kilometri.
Rezolvarea III: (algebrica)
Daca notam distanta dintre cele doua localitati cu s si tinem seama ca
t =s : v, atunci avem ecuatia:
+ 
= 9 ↔ 5s + 4s = 9 · 20 ↔ 9s = 180.
Deci s = 20 km.
2. Cu cati kilometri poate sa se indeparteze de la debarcader o barca, ce merge impotriva curentului apei, pentru ca sa se intoarca inapoi in 4 ore, daca viteza apei este de 2 km/h si viteza barcii in apa statatoare este de 8 km/h?
Indicatii si raspuns: Viteza de deplasare a barcii impotriva curentului apei este de 8 km/h - 2 km/h = 6 km/h, iar pe directia curentului apei este de
8 km/h + 2 km/h = 10 km/h. Se gaseste ca barca se poate departa de debarcader la 15 km.
f. Probleme de miscare diverse (combinate)
1. Un biciclist, deplasandu-se cu viteza de 12 km/h, pleaca din localitatea A spre localitatea B situata la 40 km de A. O data cu el, pleaca si un motociclist, cu viteza de 36 km/h. Motociclistul ajunge in B unde poposeste o ora, apoi se intoarce in intampinarea biciclistului.
Dupa cat timp de la plecarea din A, motociclistul intalneste pe biciclist si la ce distanta de A?
Rezolvare: Motociclistul a parcurs distanta de la A la B intr-un timp,
t = 40 km : 36 km/h =1 
h, dar a mai poposit
in B o ora, deci s-au scurs de la plecarea lui din A, 2 h.
In acest timp, biciclistul a parcurs distanta AC =
12 km/h · 2 h = 25 
km.
Deci, de la C la B sunt 40 km - 25 km = 14 km.
Aceasta distanta o parcurge biciclistul de la C catre B, cu 12 km/h, iar motociclistul de la B catre C cu o viteza de
40 km
A C I B
12 km/h
36 km/h
14 ⅔ km
36 km/h si astfel problema s-a redus la una de tipul cunoscut (intalnire a mobilelor cand deplasarea se face in sensuri opuse).
Deci biciclistul plecat din c, iar motociclistul din B se intalnesc in I dupa un timp:
t1
= 14 km : (12 km/h + 36
km/h) = 
h.
iar de la plecarea lor din A s-a scurs un timp:
t2
= 2 h + h = 2 
h =
2h 25 min.
Distanta AI = 12 km/h · 2 h = 29 km.
2. Un biciclist si un motociclist, antrenandu-se in cadrul unui club sportiv, pleaca din localitatea A spre localitatea B, primul la ora 8 si 30 minute, cu viteza de 8 m/s, iar al doilea la ora 8 si 45 minute, cu viteza de 25 m/s. Daca distanta de la A la B este de 20 km, sa se afle:
- la ce distanta de A motociclistul ajunge pe biciclist;
- la ce distanta fata de B este biciclistul in momentul sosirii in B a motociclistului;
- la ce ora ar fi trebuit sa plece motociclistul pentru ca el sa fi putut sosi in B o data cu biciclistul?
Indicatii
si raspuns: Viteza biciclistului este 8 m/s =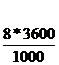 
km/h = 28,8 km/h, iar
a motociclistului de 25 m/s = 
km/h = 90 km/h.
- Prima intrebare conduce la o problema de tipul cunoscut (probleme de intalnire a mobilelor cand deplasarea se face in acelasi sens).
Se gaseste ca motociclistul il va ajunge din urma pe biciclist la distanta de
10
km departare fata de A.
- Biciclistul, in momentul sosirii motociclistului in B, se afla la distanta de 6,4 km de B.
- Pentru parcurgerea distantei de la A la B, motociclistului ii trebuie un timp
t = 20 km : 90 km/h = 
h, timp in care biciclistul parcurge distanta
d = 28,8 km/h ∙ h = 6,4 km. Deci, in
momentul plecarii motociclistului, biciclistul trebuie sa aiba
un avans de 20 km - 6,4 km = 13,6 km. Acest avans il poate lua intr-un timp:
t = 13,6 km : 28,8 km/h = 
h de mers.
Pentru a
ajunge in B, o data cu biciclistul, motociclistul trebuie sa plece
din A la ora 8h + h = 8 
h = 8 h 58 min 20 sec.
3. Un pieton a plecat din localitatea A
spre localitatea B, situate la o distanta de 20 km una fata
de alta. Dupa 1
ore a plecat din B spre el un biciclist cu viteza de 3 
ori mai mare decat a
pietonului, intalnindu-l pe acesta la jumatatea drumului. Sa se afle
viteza de mers a unuia si a celuilalt.
Rezolvare:
Fie I locul intalnirii (AI = IB = 10
km), iar C punctul in care se afla pietonul la 1 ore dupa plecare, adica in momentul cand
pleaca biciclistul. In timp ce pietonul face drumul CI, biciclistul face
drumul BI = AI = 10 km. Cum viteza biciclistului este de 3 ori mai mare ca a pietonului, BI sau AI este de 3 ori mai mare decat CI,
adica
CI = 10 : 3 = 10 ∙ 
= 2 (km), iar AC = 10 km - 2 km = 7 km.
20
km
v I 3 ¾ v
A C B
0 h 1h 1h
10 km 10
km
Pietonul parcurge drumul AC = 7 km in 1h, deci viteza sa este
v1 = 7 km : 1h = 4 km/h, iar a biciclistului v2 = 4 km/h
∙ 3 = 15 km/h.
4. Doi biciclisti au plecat in
acelasi timp din doua localitati, unul spre celalalt,
si s-au intalnit dupa 8 ore. Primul a parcurs in 6 ore o
distanta egala cu cea parcursa de cel de-al doilea in 7ore.
Cati kilometri a strabatut fiecare intr-o ora, daca distanta dintre cele doua localitati este de 180 km?
Indicatii si raspuns: Raportul vitezelor lor este egal cu raportul timpilor:
v1 : v2 = 6 : 7 = 
. Drumul de 180 km se imparte in parti direct proportionale
cu numerele 4 si 5. Se gasesc vitezele de 13 km/h si 16 km/h.
3.3. PROBLEME DE AMESTEC SI ALIAJ
a- Probleme de amestec concentratii si echilibru caloric
Unirea mai multor calitati, sau sorturi, dintr-un produs in scopul obtinerii unei noi calitati din acest produs, se numeste amestec. Orice amestec se caracterizeaza matematic prin cantitate si calitate. Cantitatea se exprima in unitati din sistemul metric, iar calitatea din pret unitar in cazul amestecului de marfuri, in grade pentru temperatura si bauturi alcoolice, in procente, pentru solutii.
Problemele de amestec, concentratii si echilibru caloric sunt de doua categorii: probleme directe si probleme inverse.
Problemele directe sunt problemele in care se dau cantitatile si calitatile produselor ce se amesteca si se cer caracteristicile amestecului.
Exemple:
Problema de amestec de marfuri.
Se amesteca 240 kg marfa de 380 lei/kg cu 150 kg de 390 lei/kg si cu 630
Kg de 410 lei/kg.
Sa se afle pretul unitar al amestecului.
Rezolvare:
Calculul se poate face utilizand expresia mediei aritmetice ponderate:
= 
= 
= 400 lei costa 1
kg de amestec.
Generalizare: Notand cu a pretul unitar al amestecului, cu a1, a2, ., an preturile unitare ale produselor, sau sorturilor, care intra in amestec, si cu k1, k2, ., kn cantitatile sorturilor respective, putem scrie expresia:
a = a1k1 + a2k2 + . + ankn
k1 + k2 + . + kn
adica pretul unitar al unui amestec este egal cu media aritmetica ponderata a preturilor unitare ale produselor, sau sorturilor, care intra in amestec.
Cazuri particulare:
* Daca k1 = k2 = . = kn = k, expresia de mai sus devine:
a = a1k + a2k + . + ank = (a1 + a2 + . + an)k = a1 + a2 + . + an
k + k + . + k nk n
Deci, in cazul cand ponderile sunt egale pretul unitar al amestecului este egal cu media aritmetica a preturilor unitare ale produselor sau sorturilor care intra in amestec.
* Daca una din partile amestecului are valoare nula, atunci acea parte intervine in calculul numai cantitativ, nu si valoric (spre exemplu in cazul solutiilor sau bauturilor alcoolice care se dilueaza cu apa).
* Daca in procesul amestecului se produc pierderi de cantitati, acestea se scad din suma ponderilor de la numitorul fractiei.
Problema de amestec de bauturi alcoolice.
La un centru de preparare a bauturilor alcoolice s-a facut in mod
experimental un amestec de 3 l rachiu de 60°, iar 4 l rachiu de 48° si 9 l rachiu de 38°, dandu-i-se o anumita aroma.
Care este taria amestecului, stiind ca in cursul procesului de preparare s-a inregistrat o pierdere de 1 l rachiu?
Rezolvare: (prin media aritmetica ponderata)
a = 
= 
= 
= 47,6.
Deci se obtine un amestec cu taria de 47,6°.
3. Problema de concentratii.
La un laborator chimic se prepara o solutie de acid clorhidric. In acest scop se pun in acelasi recipient 2 l acid cu concentratia de 15 %, 3 l acid cu concentratia de 40%, 6 l acid cu concentratia de 80% si 4 l apa distilata. Sa se afle concentratia amestecului.
Rezolvare (prin medie ponderata):
a = 
= 
= 
= 42.
b. Probleme de aliaj
Produsul metalic obtinut prin topirea laolalta a anumitor metale sau a unor metale cu metaloizi (nemetale) se numeste aliaj. Marimile care caracterizeaza un aliaj sunt: masa unui anumit metal din aliaj (se va nota cu m), masa totala a aliajului (se va nota cu M) si titlul aliajului (se va nota cu t).
Titlul este marimea care caracterizeaza calitativ un aliaj si se defineste prin raportul dintre masa unui anumit metal din compozitie si masa intregului aliaj, adica:
M = 
|
|
, de unde rezulta si
Titlul ia valori cuprinse intre zero si 1, adica 0 ≤ t ≤ 1, si se exprima, de obicei, in miimi sau promile. Daca titlul unui aliaj este nul in raport cu un anumit metal, inseamna ca acel aliaj nu contine metalul considerat, iar daca titlul este egal cu unitatea inseamna ca avem de-a face cu metalul respectiv in stare pura si nu cu un amestec de metale diferite. Notiunea de titlu se utilizeaza, cu deosebire, pentru aliajele care contin metale pretioase: aur, argint, platina.
Problemele de aliaj se pot referi la un singur aliaj sau la doua ori mai multe aliaje.
Cele relative la un singur aliaj sunt de doua feluri:
Probleme de determinare a uneia din marimile care caracterizeaza un aliaj
1. Determinarea titlului unui aliaj
cunoscand masa m a metalului pretios si masa totala M a
aliajului, se face prin aplicarea formulei t = 
.
Exemplu: Sa se afle titlul aurului dentar stiind ca 75 g din acest aliaj contine 68,7 g aur pur.
Rezolvare: t = 
= 0,916.
2. Determinarea masei metalului pretios dintr-un aliaj cunoscand masa totala M a aliajului si titlul sau t, se face prin aplicarea formulei m = M t.
Exemplu: Sa se afle cat argint pur contine o cupa cu masa de 460 g confectionata dintr-un aliaj de argint cu titlul 0,815.
Rezolvare: m = 460 g ∙0,815 = 374,9 g.
3. Determinarea unei mase totale a unui
aliaj cunoscand titlul t si masa m a metalului pretios. In acest caz
se aplica formula M = .
Exemplu: O bratara confectionata dintr-un aliaj de aur de 14 carate contine 18,656 g aur pur. Sa se afle masa obiectului.
Rezolvare: Daca aliajul este de 14
carate si stiind ca aurul pur are 24 carate, inseamna
ca titlul aliajului este dat de fractia 
= 0,583. Acum, cunoscand titlul aliajului si masa
metalului pretios, putem calcula masa totala a aliajului: M = 
= 32 g.
Pentru rezolvarea problemelor de aliaj de categoria a II-a pare mai comoda si mai eleganta metoda care utilizeaza diferentele titlurilor aliajelor care intra in amestec fata de aliajul final. Pentru a stabili relatia respectiva, scriem media ponderata a titlurilor a doua aliaje:
t = t1M1 + t2M2 .
M1 + M2
Prin eliminarea numitorului obtinem: tM1 + tM2 = t1M1 + t2M2. Se separa termenii astfel ca ponderile M1 si M2 sa se afle unul de o parte, altul de cealalta parte a egalitatii:
tM1 - t1M1 = t2M2 - tM2 → (t - t1)M1 = (t2 - t)M2 → M1 = t2 - t .
M2 t - t1
In cuvinte, relatia obtinuta se citeste astfel: Raportul maselor a doua aliaje care intra in amestec este egal cu raportul invers al diferentelor titlurilor acelor aliaje fata de titlul final.
Pentru stabilirea diferentelor titlurilor fata de titlul mediu este indicat sa se utilizeze urmatoarea schema, aceasta prezentand doua avantaje: ofera o privire de ansamblu asupra relatiilor dintre titluri si realizeaza inversarea raportului acestor diferente:
M1 t1 t2 - t
t , pentru cazul t1 < t < t2 .
M2 t2 t - t1
In rezolvarea problemei de mai sus, schema se prezinta astfel:
0,836 0,040
0,860
0,900 0,024
Observatii: 1) Schema de mai sus se poate utiliza si in problemele inverse de amestec, concentratii si echilibru caloric.
2) In unele probleme de amestec, concentratii si aliaj sunt eficiente si alte metode aritmetice de rezolvare, cu deosebire metoda falsei ipoteze.
3) In cazul cand problemele de aliaj (categoria a II-a) se refera la mai mult de doua marimi, atunci ele trebuie sa contina relatii pe baza carora sa se reduca la doua marimi.
Exemple:
. Doua aliaje de aur, primul cu titlul 0,950, al doilea cu titlul 0,800 se topesc impreuna cu 20 g aur pur, obtinandu-se un nou aliaj cu masa de 250 g si titlul 0,906. Sa se afle masa fiecaruia din cele doua aliaje.
Rezolvare:
M1 = . m1 = . t1 = 0,950
M2 = . m2 = . t2 = 0,800
M3 = 20 g m3 = 20 g t3 = 1
M = 250 g m = . t = 0,906
Problema se reduce cu usurinta la doua marimi, intrucat celei de-a treia i se cunosc toate elementele. Atunci avem: M1 + M2 + M3 = 250 g, unde M3 = 20 g, deci M1 + M2 = 230 g.
Scriind expresia mediei ponderate a titlurilor aliajelor care intra in amestec obtinem egalitatea:
0,906 = 0,950 M1 + 0,800 M2 + 1 ∙ 20 , in care M1 + M2 = 230 si efectuand
250
calculele, obtinem: M1 = 150 g, M2 = 80 g.
2. Un aliaj de argint cu masa de 400 g si titlul 0,820 se topeste cu alte doua aliaje de mase egale, avand titlurile 0,800, respectiv 0,750. Se obtine un nou aliaj cu titlu 0,793. Sa se afle masele aliajelor care intra in amestec.
Rezolvare:
M1 = 400 g m1 = . t1 = 0,820
M2 = . m2 = . t2 = 0,800 unde
M3 = . m3 = . t3 = 0,750 M2=M3
M = 400 + 2M2 m = . t = 0,793
Expresia mediei ponderate a titlurilor aliajelor care formeaza compozitia se scrie:
0,793 = 0,820 ∙400 + 0,800 M2 + 0,750 M2 . Aceasta egalitate contine o singura
400 + 2M2
necunoscuta M2. Efectuand calculele se obtine:
M2 = M3 = 300 g. Deci M = M1 + M2 + M3 = 400 g + 300 g + 300 g = 1000 g.
|
Politica de confidentialitate |
 .com |
Copyright ©
2024 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |
