Prin capacitatea portanta a terenului de fundare se intelege incarcarea pe care o poate suporta aceasta, fara ca deformatiile sale sa compromita buna exploatare a constructiei pentru care serveste ca suport.
La depasirea unei anumite valori a tensiunii transmise in terenul de fundare are loc ruperea acestuia, cu efecte catastrofale si poate compromite partial sau total stabilitatea constructiei.
Pentru explicarea fenomenului de rupere a terenului de fundare trebuie efectuate incarcari progresive pana la rupere. S-a constatat ca atunci cand incarcarea creste incet, rezultatul este o compactare a terenului de sub talpa fundatiei, iar in diagrama compresiune - tasare se obtine o variatie liniara. In aceasta faza, granulele se misca de sus in jos pe directie verticala, avand mici devieri laterale.
Cresterea in continuare a incarcarii are drept consecinta o accelerare a cresterii tasarilor, astfel incat dependenta tensiune - tasare capata un caracter neliniar. In terenul de fundare in afara fenomenelor de tasare incep sa se dezvolte alunecari. Acestea apar initial in puncte izolate in jurul carora procesele de alunecare se extind o data cu cresterea incarcarii.
Pentru a defini concret notiunea de capacitate portanta se considera o fundatie incarcata cu o forta concentrata N, normala si centrica, fig.3.5.
Presiunea de contact la nivelul talpii fundatiei va avea valoarea:
![]()
![]() . (3.18)
. (3.18)
Marind valoarea fortei concentrate N si masurand deformatia terenului de fundare, corespunzatoare fiecarei trepte de solicitare, se poate reprezenta diagrama de variatie a tasarii e in functie de presiunea de contact.
Pe curba tensiune-tasare se pot pune in evidenta trei sectoare caracteristice procesului de deformare a terenului de fundare.
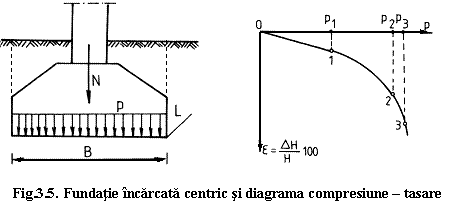
Sectorul 0-1 este caracterizat prin relatia de dependenta liniara intre tensiune si deformatie. Diagrama pe acest domeniu se poate aproxima cu o dreapta.
Tasarile suferite de terenul de fundare se datoresc in exclusivitate reducerii porozitatii, iar faza de deformare a terenului poarta denumirea de "faza de indesare".
Sectorul 1-2 corespunde unor deformatii neliniare. Aceastea, pe de o parte sunt date de tasarea terenului si pe de alta parte de deformatiile de alunecare produse de eforturile tangentiale. La apropierea presiunii de contact de o anumita valoare p2, se poate ajunge la depasirea rezistentei la forfecare a pamantului, fapt care conduce la formarea unor zone plastice. Aceasta faza este denumita "faza alunecarilor" sau "faza zonelor plastice".
Presiunea corespunzatoare acestei faze se numeste presiune de plasticizare, ppl si are semnificatia de presiune acceptabila pentru terenul de fundare.
Sectorul 2-3 corespunde unor cresteri accentuate ale deformatiilor, datorita extinderii zonelor plastice si formarii unor suprafete de cedare - alunecare.
Pentru o anumita valoare a presiunii de contact p = p3 = pcr, terenul de fundare ajunge la starea limita a capacitatii portante, in care se produce ruperea si refularea pamantului de sub fundatie, de-a lungul suprafetelor de cedare formate.
Aceasta faza se numeste "faza de rupere" sau "faza de cedare", iar presiunea corespunzatoare acestei faze reprezinta "presiunea critica".
Pornind de la constatarile expuse anterior privind modul de evolutie al deformatiilor pana in momentul in care se produce ruperea terenului de fundare s-au elaborat o serie de metode de calcul pentru determinarea capacitatii portante in care se tine seama de fazele posibile ale comportamentului terenului de fundare.
Astfel, daca se considera o incarcare uniform distribuita, crescatoare, aceasta va duce la un moment dat la aparitia unui echilibru limita, pentru o anumita marime a incarcarii. Cresterea incarcarii exterioare determina inmultirea punctelor in care este atins echilibrul limita, aparand o zona de echilibru limita.
In punctele in care are loc starea de echilibru limita se presupune ca sunt valabile simultan atat relatiile din teoria elasticitatii cat si cele din teoria plasticitatii.
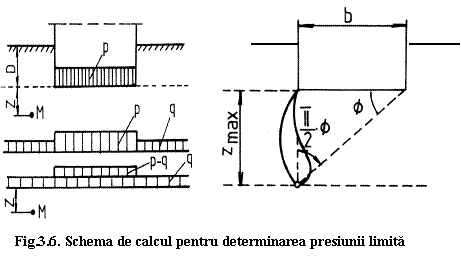
Pentru
determinarea zonei echilibrului limita se porneste de la o
schema de incarcare prezentata in fig.3.6.
Se considera ca greutatea pamantului situat deasupra talpii fundatiei se poate inlocui cu tensiunea verticala q de origine gravitationala. Din punct de vedere mecanic, starea de echilibru limita corespunde starii plastice, cand deformatia se produce fara modificarea volumului, n = 0,5.
In punctul M, la cota z, tensiunile normale principale vor fi:
- tensiunea data de greutatea masivului:
![]() , (3.19)
, (3.19)
![]() .
(3.20)
.
(3.20)
Pentru n= 0,5 rezulta:
![]() . (3.21)
. (3.21)
Tensiunile date de incarcarea uniform distribuita de valoare p - g D vor fi:
![]() , (3.22)
, (3.22)
![]() . (3.23)
. (3.23)
Valoarea totala a tensiunilor normale principale in punctul M va fi:
![]() , (3.24)
, (3.24)
![]() . (3.25)
. (3.25)
Introducand aceste relatii in conditia de echilibru limita si explicitand adancimea z, se obtine:
![]() (3.26)
(3.26)
unde: ![]() .
.
Aceasta relatie
reprezinta ecuatia liniei care separa domeniul
deformatiilor elastice de domeniul deformatiilor plastice, care
pentru ![]() devine:
devine:
![]() . (3.27)
. (3.27)
In cazul in care se considera ipoteza ruperii terenului de fundare, admitandu-se implicit dezvoltarea maxima a zonelor de deformatie plastica prin aparitia in terenul de fundare a unor zone continue de echilibru limita, pentru rezolvarea problemei se pot aborda urmatoarele directii:
se rezolva problema prin intermediul aplicarii ecuatiilor diferentiale de echilibru limita, punandu-se conditiile la limita, corespunzatoare problemei date;
se admite o anumita forma pentru suprafetele de alunecare de sub fundatie, astfel incat tensiunea de rupere se determina pe baza ecuatiilor de echilibru static in acel moment.
Teoria lui Terzaghi privind capacitatea portanta a terenului de fundare pleaca de la presiunea critica, presiune care poate duce la cedarea terenului de fundare.
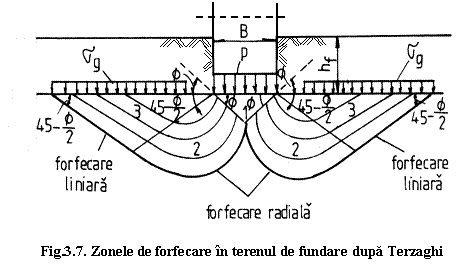
Modelul conceptual de cedare a terenului de fundare este prezentat in fig. 7.7.
Terzaghi studiaza capacitatea portanta pentru fundatii considerand terenul de fundare omogen.
Se considera o fundatie de latime B, situata la adancimea hf, care transmite terenului o presiune crescatoare p. Sub efectul incarcarii, rocile se compacteaza, prin reducerea treptata a porozitatii. Zona compactata are forma unui con, orientat cu varful in jos care face cu orizontala un unghi egal cu unghiul de frecare interioara f. Crescand incarcarea pe terenul de fundare, zona 1 coboara pe verticala, iar efectul ei de "pana" produce ruperea terenului. Se disting doua zone (2) marginite de suprafete curbe si doua zone de forfecare liniara (3).
Ecuatiile stabilite de Terzaghi pentru diferite tipuri de fundatii de suprafata
sunt:
- fundatii tip talpa continua:
![]() , (3.28)
, (3.28)
- fundatii patrate:
![]() , (3.29)
, (3.29)
- fundatii circulare:
![]() , (3.30)
, (3.30)
unde: pcr - capacitatea portanta critica a terenului de fundare, in kPa;
g - greutatea volumica a terenului, kN/m3;
B - latimea fundatiei, in m;i
L - lungimea fundatiei, in m;
D - diametrul fundatiei, in m;
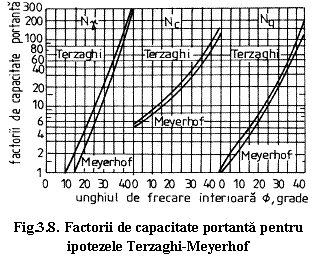
Ng, Nc, Nq - factori de capacitate portanta adimensionali, care se determina in functie de unghiul de frecare interioara, pe cale analitica sau grafica;
c - coeziunea terenului de fundare, in kPa.
Capacitatea portanta determinata prin ecuatiile stabilite de Terzaghi, are valori care depasesc cu mult presiunea maxima pe terenul de fundare, mai ales in cazul fundatiilor cu dimensiuni mari, fapt ce ar conduce la tasari mai mari sau cel mult egale cu tasarea admisibila pentru o constructie data.
Skempton a propus valori mai mari pentru coeficientul de siguranta, ceea ce a condus la urmatoarele ecuatii modificate:
- fundatii sub forma de talpa:
![]() , (3.31)
, (3.31)
- fundatii patrate:
![]() , (3.32)
, (3.32)
- fundatii circulare:
![]() . (3.33)
. (3.33)
Capacitatea portanta critica obtinuta cu relatiile: 3.31, 3.32 si 3.33 se imparte la coeficientul de siguranta h si se obtine capacitatea portanta admisibila a terenului de fundare:
![]() . (3.34)
. (3.34)
Meyerhof a studiat solutia data de Terzaghi si a ajuns la o ecuatie asemanatoare de forma:
![]() ; (3.35)
; (3.35)
in care: p0 - este presiunea normala pe "suprafata libera" echivalenta care pleaca din coltul fundatiei, sub unghiul b0 si iese la suprafata terenului.
Suprafata libera echivalenta este un plan inclinat, cuprins intre suprafata terenului si adancimea de fundare care face cu orizontala unghiul b0.
Presiunea p0 se poate determina pe baza tensiunii verticale de origine gravitationala:
p0 = 0,5 g hf. (3.36)
Tinand seama de ecuatia 7.36 ecuatia 7.35![]() devine:
devine:
![]() . (3.37)
. (3.37)
Pentru un teren de fundare format din mai multe strate de pamant vom avea:
![]() . (3.38)
. (3.38)
Factorii de capacitate portanta Ng, Nc si Nq sunt determinati in functie de unghiul de frecare interioara si se determina cu ajutorul nomogramelor din figura 3.8.
Aceasta metoda permite determinarea presiunii admisibile pe teren, presiune egala cu tensiunea la limita plastica corespunzatoare unei anumite dezvoltari a zonelor plastice in terenul de fundare, fig. 3.9.
Pentru determinarea tensiunii la limita de plasticizare se considera o fundatie continua cu latimea B situata la adancimea Df si care transmite terenului de fundare presiunea uniform repartizata p.
La nivelul talpii fundatiei presiunea litologica are valoarea:
q = g D. (3.39)
Presiunea neta este data de relatia:
pn = p - g D. (3.40)
Starea de tensiune intr-un punct oarecare M, unde talpa fundatiei se vede sub unghiul 2q0, poate fi exprimata cu relatiile din teoria elasticitatii, pentru un semiplan incarcat cu o sarcina distribuita pe o portiune finita. Tensiunile generate de presiunea neta se exprima cu relatiile:
![]() ,
,
![]() , (3.41)
, (3.41)
![]() .
.
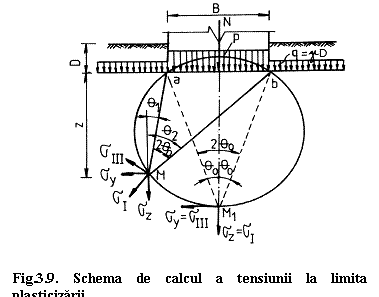
Intr-un punct M1, situat pe axa de simetrie a fundatiei, din care latimea acesteia se vede sub acelasi unghi 2q0 (numit unghi de vedere), unghiurile q1 q0 si q2 q0, tensiunile sz sy, devin tensiuni principale. In aceste conditii relatiile 3.41 devin:
![]() ,
,
![]() , (3.42)
, (3.42)
![]() .
.
Din analiza relatiilor 3.42 rezulta ca tensiunile principale generate de incarcarea exterioara depind de valoarea presiunii p si de unghiul de vedere 2q
Pentru o anumita valoare a presiunii p, tensiunile au aceiasi valoare, in punctele carora le corespunde acelasi unghi de vedere 2q0. Locul geometric al acestor puncte este un cerc care trece prin marginile fundatiei si prin punctul M.
In punctul M1 situat la adancimea z sub talpa fundatiei, sarcina geologica genereaza tensiunile principale:
![]() ,
,
![]() , (3.43)
, (3.43)
unde: ![]() - coeficientul presiunii laterale.
- coeficientul presiunii laterale.
Prin suprapunerea efectelor sarcinilor create de greutatea fundatiei a constructiei si a componentelor starii de tensiune gravitationala se obtin tensiunile principale totale:
![]() , (3.44)
, (3.44)
Din relatiile 3.44 se constata ca in punctele situate pe acelasi cerc si caracterizate prin acelasi unghi 2q0, tensiunile nu mai sunt constante fiind dependente de adancimea z.
Pentru punerea unor conditii de limitare a dezvoltarii zonelor plastice in terenul de fundare, este necesara determinarea adancimii z, pana la care acestea pot sa apara sub actiunea tensiunilor principale totale s1 si s3. Pentru aceasta se foloseste conditia de plasticitate Mohr-Coulomb, exprimata analitic prin relatia:
![]() . (3.45)
. (3.45)
Inlocuind tensiunile principale totale date de relatiile 3.44 in relatia 3.45 se obtine adancimea cautata z:
![]() . (3.46)
. (3.46)
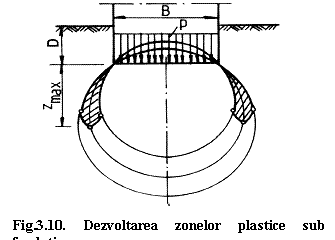
In terenul de fundare pot exista mai multe puncte, care apar pe cercuri diferite ce trec prin marginile fundatiei, in care se pot produce deformatii plastice sub actiunea acelorasi incarcari p, fig. 3.10. Ne intereseaza insa adancimea maxima zmax pana la care se pot extinde zonele plastice in terenul de fundare.
In acest scop se pune conditia de maxim pentru functia z = f(2q0), adica:
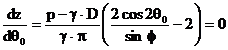 . (3.47)
. (3.47)
Din
ecuatia 3.47 rezulta ca: 2![]() . (3.48)
. (3.48)
Prin inlocuirea relatiei 3.48 in relatiile 3.46 se obtine:
![]() . (3.49)
. (3.49)
Pornind de la relatiile 3.49, metodele de determinare a tensiunii la limita plasticizarii se deosebesc intre ele prin ipotezele facute asupra marimii lui zmax.
Astfel Fröhlich si Puzarevschi au pus conditia ca la stabilirea presiunii admisibile pe terenul de fundare sa nu apara zone de curgere plastica:
zmax = 0 (3.50)
Din conditia 3.50 si ecuatia 3.49 rezulta:
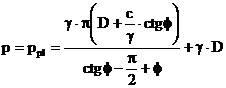 . (3.51)
. (3.51)
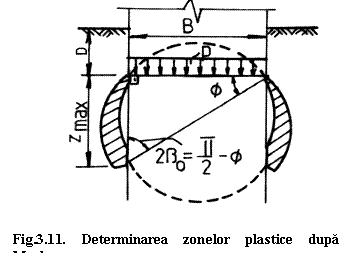
O alta metoda de determinare a capacitatii portante emisa de Maslov, admite ca zonele plastice sa se extinda numai in exteriorul verticalelor duse prin marginile fundatiei, fig.3.11.
Conform acestei conceptii rezulta:
zmax = B tg f (3.52)
Din conditia 7.52 si relatia 7.49 rezulta:
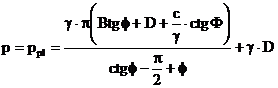 . (3.53)
. (3.53)
Se constata ca in aceasta relatie intervine si latimea fundatiei B.
Conform prevederilor STAS 3300/2-85, "Calculul terenului de fundare in cazul fundarii directe", se limiteaza extinderea zonelor plastice in teren pana la adancimea:
zmax = B/4, (3.54)
si rezulta:
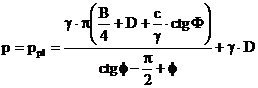 . (3.55)
. (3.55)
Gruparea termenilor din relatia 3.55, permite rescrierea presiunii de plasticizare, conform STAS 3300/2-85, sub forma generala:
![]() , [kPa] (3.56)
, [kPa] (3.56)
in care:![]() - media ponderata a greutatii volumice de
calcul a straturilor de sub
- media ponderata a greutatii volumice de
calcul a straturilor de sub
fundatie, cuprinse pe o adancime B/4 masurata de la talpa fundatiei, in
kN/m3;
B - latimea talpii fundatiei, in m;
q - suprasarcina de calcul la cota talpii fundatiei, in kPa;
c - valoarea de calcul a coeziunii specifice a stratului de pamant de sub talpa fundatiei, in kPa;
N1, N2, N3 - coeficienti adimensionali a caror valoare se determina din tabelul 3.1, in functie de valoarea de calcul a unghiului de frecare interioara a pamantului de sub talpa fundatiei.
Presiunea de plasticizare, ppl, in cazul fundatiilor izolate cu forma dreptunghiulara in plan, se calculeaza cu relatiile:
- pentru constructii fara subsol:
![]() ,[kPa] (3.57)
,[kPa] (3.57)
- pentru constructii cu subsol:
![]() .[kPa] (3.58)
.[kPa] (3.58)
in care: ml - coeficient al conditiilor de lucru, conform tabelului 3.2;
B - latura mica a fundatiei dreptunghiulare, in m;
qe, qi - suprasarcina de calcul la nivelul talpii fundatiei, la exteriorul si respectiv interiorul fundatiei din zona subsolului, in kPa.
Presiunea efectiva pe teren la nivelul talpii fundatiei, pef, provenita din incarcarile de calcul din gruparea fundamentala, pentru care se efectueaza calculul la starea limita de deformatii, nu va depasi valoarea limita a presiunii de plasticizare, adica:
pef = a ppl, (3.59)
in care: a - coeficient care tine seama de tipul solicitarii exterioare; a = 1 in cazul solicitarii centrice, a = 1,2 in cazul solicitarii excentrice pe o directie si a = 1,4 in cazul solicitarii excentrice pe doua directii.
Tabelul 3.1.
Valorile coeficientilor N1, N2, N3.
|
Fo |
N1 |
N2 |
N3 |
Fo |
N1 |
N2 |
N3 |
|
0 |
0,00 |
1,00 |
3,14 |
24 |
0,72 |
3,87 |
6,45 |
|
2 |
0,03 |
1,12 |
3,32 |
26 |
0,84 |
4,37 |
6,90 |
|
4 |
0,06 |
1,25 |
3,51 |
28 |
0,98 |
4,93 |
7,40 |
|
6 |
0,10 |
1,39 |
3,71 |
30 |
1,15 |
5,59 |
7,95 |
|
8 |
0,14 |
1,55 |
3,93 |
32 |
1.34 |
6,35 |
8,55 |
|
10 |
0,18 |
1,73 |
4,17 |
34 |
1,55 |
7,21 |
9,21 |
|
12 |
0,23 |
1,94 |
4,42 |
36 |
1,81 |
8,25 |
9,98 |
|
14 |
0,29 |
2.17 |
4,69 |
38 |
2,11 |
9,44 |
10,80 |
|
16 |
0,36 |
2,43 |
5,00 |
40 |
2,46 |
10,84 |
11,73 |
|
18 |
0,43 |
2.72 |
5,31 |
42 |
2,87 |
12,50 |
12,77 |
|
20 |
0,51 |
3,06 |
5,66 |
44 |
3,37 |
14,48 |
13,96 |
|
22 |
0,61 |
3,44 |
6,04 |
45 |
3,66 |
15,64 |
14,64 |
Tabelul 3.2.
Coeficientii conditiilor de lucru ml
|
Nr. crt. |
Denumirea terenului de fundare |
ml |
|
1. |
Bolovanisuri cu interspatiile umplute cu nisip, pietrisuri si nisipuri cu exceptia nisipurilor fine si prafoase. |
2,00 |
|
2. |
Nisipuri fine: - uscate sau umede (Sr 0,8) - foarte umede sau saturate (Sr > 0,8) |
1,90 1,80 |
|
3. |
Nisipuri prafoase: - uscate sau umede (Sr 0,8) - foarte umede sau saturate (Sr > 0,8) |
1,80 1,50 |
|
4. |
Bolovanisuri si pietrisuri umplute cu pamanturi argiloase cu Ic 0,5 |
1,60 |
|
5. |
Pamanturi argiloase cu Ic 0,5 |
1,60 |
|
6. |
Bolovanisuri si pietrisuri umplute cu pamanturi argiloase cu Ic < 0,5 |
1,10 |
|
7. |
Pamanturi argiloase cu Ic < 0,5 |
1,10 |
Aceasta metoda se bazeaza pe starea de echilibru limita in determinarea capacitatii portante a terenului de fundare.
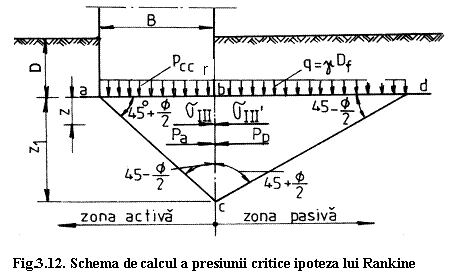
In cazul in care presiunea de contact atinge valoarea critica p = pcr, terenul de fundare ajunge la limita capacitatii portante, la care se produce ruperea si refularea terenului de fundare de-a lungul unor suprafete de cedare, suprafete pe care rezistenta la forfecare este depasita, fig. 3.12.
Rankine a admis, pentru o fundatie continua de latime B si care transmite terenului de fundare o presiune de contact p = pcr, ipoteza simplificatoare ca ruperea si refularea rocilor are loc numai pe o parte a fundatiei, dupa suprafete plane ac si cd, si aceste suprafete plane sunt considerate planurile de alunecare corespunzatoare impingerii active si a rezistentei pasive in cazul unui zid de sprijin.
Pentru determinarea presiunii critice se analizeaza starea de echilibru, in conditiile problemei plane, pe suprafata verticala bc asupra careia actioneaza impingerea prismei de pamant abc si suprasarcina pcr, respectiv rezistenta pasiva data de prisma bcd si suprasarcina q = g D.
La o anumita adancime z, tensiunile principale verticale au valorile:
- pentru zona activa:
s1 = pcr + g z; (3.60)
- pentru zona pasiva:
![]() . (3.61)
. (3.61)
Din conditia de rupere Coulomb - Mohr tensiunea principala secundara s3 este data de relatia:
![]() . (3.62)
. (3.62)
Relatia 7.62 se mai poate scrie:
![]() , (3.63)
, (3.63)
unde: Ka - coeficientul impingerii active:
Ka
= tg2 ![]() .
.
Inlocuind relatia 3.60 in relatia 3.63 se obtine:
![]() . (3.64)
. (3.64)
In mod similar se poate determina si tensiunea secundara pentru zona pasiva:
![]() , (3.65)
, (3.65)
sau:
![]() , (3.66)
, (3.66)
in care: Kp - coeficientul rezistentei pasive:
Kp=
![]() .
.
Tensiunile principale secundare s3 si ![]() , pe adancimea z1, sunt egale cu impingerile
active si rezistentele pasive:
, pe adancimea z1, sunt egale cu impingerile
active si rezistentele pasive:
![]() , (3.67)
, (3.67)
pp
= ![]() . (3.68)
. (3.68)
Din triunghiul abc, rezulta:
![]() . (3.69)
. (3.69)
Conditia de echilibru limita, pe suprafata bc, se poate scrie din egalarea presiunii active si pasive:
Pa = Pp. (3.70)
Prin inlocuirea relatiilor 3.67, 3.68 si 3.69 in relatia 3.70 se obtine valoarea presiunii critice:
![]() . (3.71)
. (3.71)
Daca facem notatiile:
![]() , (3.72)
, (3.72)
relatia 3.71 se poate scrie:
![]() , (3.73)
, (3.73)
in care: Ng, Nc si Nq sunt coeficienti adimensionali, care caracterizeaza capacitatea portanta, a caror valori sunt in functie de valoarea de calcul a unghiului de frecare interioara a terenului de sub talpa fundatiei.
Conform STAS 3300/2-85 presiunea critica se poate determina, atunci cand rezultanta incarcarilor de calcul are o inclinare mai mica de 5o si in conditiile unei stratificatii orizontale, cu relatia:
pcr = g B Ng lg + q Nq lq + c Nc lc [kPa] (3.74)
in care: g - greutatea volumica de calcul a straturilor de pamant de sub talpa fundatiei, in kPa;
B - latimea redusa a talpii fundatiei, in m;
q - suprasarcina de calcul care actioneaza la nivelul talpii fundatiei, lateral fata de fundatie, in kPa;
c - valoarea de calcul a coeziunii straturilor de pamant de sub talpa fundatiei,
in kPa;
Ng, Nq, Nc - coeficienti de capacitate portanta care depind de valoarea de calcul a unghiului de frecare interioara a straturilor de pamant de sub talpa fundatiei, conform tabelului 3.3.
lg lq lc - coeficienti de forma ai talpii fundatiei, conform tabelului 3.4.
Tabelul 3.3.
Valorile coeficientilor Ng, Nq, Nc
|
Fo |
Nr |
Nq |
Nc |
|
0o |
0,0 |
1,0 |
5,1 |
|
5o |
0,1 |
1,6 |
6,5 |
|
10o |
0,2 |
2,5 |
8,3 |
|
15o |
0,7 |
3,9 |
11,0 |
|
20o |
1,8 |
6,4 |
14,8 |
|
22o30 |
2,7 |
8,2 |
17,5 |
|
25o |
4,1 |
10,7 |
20,7 |
|
27o30 |
6,1 |
13,9 |
24,9 |
|
30o |
9,0 |
18,4 |
30,1 |
|
32o30 |
13,6 |
24,6 |
37,0 |
|
35o |
20,4 |
33,3 |
46,1 |
|
37o30 |
31,0 |
45,8 |
58,4 |
|
40o |
47,7 |
64,2 |
75,3 |
|
42o30 |
75,0 |
91,9 |
99,3 |
|
45o |
120,5 |
134,9 |
133,9 |
In cazul prezentei sub fundatie a unei stratificatii in care caracteristicile de rezistenta la forfecare, f si c, nu difera cu mai mult de 50% fata de valorile medii, se pot adopta pentru calculul capacitatii portante valori f, c si g ca medii ponderate ale straturilor de pamant.
In calculul terenului de fundare la starea limita de capacitate portanta, incarcarea de calcul care actioneaza asupra fundatiei provine din gruparea speciala iar capacitatea portanta a terenului de fundare este cea a presiunii critice, de cedare a terenului.
Tabelul 3.4.
Valorile coeficientilor lg lq lc
Forma fundatiei |
lc lq |
lg |
|
- Continua |
1,0 |
1,0 |
|
- Dreptunghiulara B/L 0,2 |
1 + 0,3 B /L |
1 - 0,4 B /L |
|
- Patrat, cerc |
1,3 |
0,6 |
In cazul fundatiilor directe cu talpa fundatiei orizontala, presiunea efectiva nu trebuie sa depaseasca valoarea de calcul a presiunii critice:
pef 0,90 pcr [kPa] (3.75)
in care: pef - presiunea medie efectiva care actioneaza la talpa fundatiei, provenita din actiunea incarcarilor de calcul corespunzatoare celei mai defavorabile grupari speciale, in kPa;
pcr - presiunea critica corespunzatoare cedarii generale a terenului de fundare, calculata cu relatia 3.74.
Din paragrafele anterioare se observa ca pentru calculul marimii presiunii de plasticizare ppl si a presiunii critice pcr este obligatorie cunoasterea valorilor de calcul ale parametrilor geotehnici, fizici si de rezistenta, ai terenului de fundare dar si a dimensiunilor fundatiilor respective. De aceea, la dimensionarea fundatiilor este obligatorie elaborarea studiului geotehnic al amplasamentului. Elaborarea studiului geotehnic este obligatorie si in cazul constructiilor existente, la care urmeaza sa se modifice substantial regimul de incarcare, prin schimbarea destinatiei sau supraetajarii.
La stabilirea preliminara a dimensiunilor talpii fundatiilor, STAS 3300/2-85 admite calculul terenului de fundare pe baza presiunilor conventionale pconv, presiuni acceptabile ale terenului de fundare determinate in mod empiric din tabelele 3.6 si 3.7, din Anexa B a instructiunii tehnice mentionate. Calculul infrastructurii pe baza presiunilor empirice pconv, se admite si in cazul constructiilor care fac parte din clasa de importanta IV, V si unele din clasa III.
Prin calculul preliminar sau definitiv al terenului de fundare pe baza presiunilor conventionale, trebuie sa se respecte urmatoarea conditie:
pef max a pconv; [kPa] (3.76)
in care:
pef max - reprezinta presiunea efectiva maxima pe teren, provenita din incarcarile de calcul din gruparea fundamentala sau speciala, in kPa;
a - coeficient in functie de natura solicitarii, conform tabelului 3.5;
pconv - presiunea
conventionala a terenului de fundare determinata in functie
de presiunea conventionala de baza ![]() si corectata in functie de latura mica a
fundatiei si de cota de fundare, conform relatiei 3.77.
si corectata in functie de latura mica a
fundatiei si de cota de fundare, conform relatiei 3.77.
|
Gruparea incarcarilor de calcul |
Tipul de solicitare |
||
|
Centrica |
Excentrica dupa o directie |
Excentrica dupa doua directii |
|
|
Fundamentala |
1,00 |
1,20 |
1,40 |
|
Speciala |
1,20 |
1,40 |
1,60 |
Valorile presiunilor
conventionale de baza ![]() , pentru pamanturile necoezive si cele coezive sunt
redate in tabelele 3.6, respectiv 3.7, conform STAS 3300/2-85.
, pentru pamanturile necoezive si cele coezive sunt
redate in tabelele 3.6, respectiv 3.7, conform STAS 3300/2-85.
Presiunile conventionale de
baza, ![]() , corespund unor fundatii cu latimea
talpii B = 1,00 m si cota de fundare D = 2,00 m.
, corespund unor fundatii cu latimea
talpii B = 1,00 m si cota de fundare D = 2,00 m.
Pentru alte situatii, presiunea conventionala se calculeaza cu relatia:
![]() ; [kPa] (7.77)
; [kPa] (7.77)
Tabelul 3.6.
Valorile presiunii
conventionale de baza ![]() pentru unele pamanturi necoezive
pentru unele pamanturi necoezive
Denumirea terenului de fundare |
Indesare |
Indesare medie |
||
|
pconv[kPa] |
||||
|
Nisip mare |
700 |
600 |
||
|
Nisip mijlociu |
600 |
500 |
||
|
Nisip fin |
uscat sau umed |
500 |
350 |
|
|
foarte umed sau saturat |
350 |
250 |
||
|
Nisip fin prafos |
uscat |
350 |
250 |
|
|
umed |
250 |
200 |
||
|
foarte umed sau saturat |
200 |
150 |
||
Tabelul 3.7
Valorile presiunii
conventionale de baza ![]() pentru unele pamanturi coezive
pentru unele pamanturi coezive
Denumirea terenului de fundare |
Indicele porilor e |
Consistenta |
|
|
Ic = 0,5 |
Ic = 1,0 |
||
|
pconv [kPa] |
|||
|
Cu plasticitate redusa (Ip 10%): nisip argilos, praf nisipos, praf |
0,5 |
300 |
350 |
|
0,7 |
275 |
300 |
|
|
Cu plasticitate mijlocie (10% < Ip 20%): nisip argilos, praf nisipos argilos, praf argilos, argila prafoasa-nisipoasa, argila nisipoasa, argila prafoasa |
0,5 |
300 |
350 |
|
0,7 |
275 |
300 |
|
|
1,0 |
200 |
250 |
|
|
Cu plasticitate mare si foarte mare(Ip > 20%): argila nisipoasa, argila prafoasa, argila, argila grasa |
0,5 |
550 |
650 |
|
0,6 |
450 |
525 |
|
|
0,8 |
300 |
350 |
|
|
1,1 |
225 |
300 |
|
Pentru alte situatii, presiunea conventionala se calculeaza cu relatia:
![]() ; [kPa] (3.78)
; [kPa] (3.78)
in care: ![]() - valoarea de baza a presiunii conventionale,
conform tabelelor 3.6 si 3.7, in kPa;
- valoarea de baza a presiunii conventionale,
conform tabelelor 3.6 si 3.7, in kPa;
CB - corectia presiunii functie de latime, in kPa;
CD - corectia presiunii functie de adancime, in kPa.
Corectia de latime CB se determina astfel:
- pentru fundatii cu B 5 m:
![]() ; [kPa] (3.79)
; [kPa] (3.79)
in care: K1 = 0,10 - pentru pamanturi necoezive cu exceptia nisipurilor prafoase;
K1 = 0,05 - pentru nisipuri prafoase si pamanturi coezive.
- pentru fundatii cu B > 5 m:
CB = 0,40 ![]() - pentru pamanturi necoezive in kPa;
- pentru pamanturi necoezive in kPa;
CB = ![]() - pentru
pamanturi coezive in kPa.
- pentru
pamanturi coezive in kPa.
Corectia de adancime CD se determina cu relatiile:
- pentru D < 2,0 m: ![]() ; [kPa] (3.80)
; [kPa] (3.80)
- pentru D > 2,0 m :
![]() ; [kPa] (3.81)
; [kPa] (3.81)
in
care: ![]() - greutatea volumica medie ponderata a straturilor
situate deasupra cotei de fundare, in kN/m3;
- greutatea volumica medie ponderata a straturilor
situate deasupra cotei de fundare, in kN/m3;
K2 - coeficient conform tabelului 3.8.
Tabelul 3.8.
Coeficient K2
Denumirea pamanturilor |
K2 |
|
Pamanturi necoezive, cu exceptia nisipurilor prafoase |
2,5 |
|
Nisipuri prafoase, pamanturi coezive cu plasticitate redusa si mijlocie |
2,0 |
|
Pamanturi coezive cu plasticitate mare si foarte mare |
1,5 |
La constructiile cu subsol se adopta pentru calculul presiunilor conventionale, valorile corectiilor corespunzatoare adancimii de fundare masurate de la nivelul pardoselii subsolului la nivelul talpii fundatiei.
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |