
DINAMICA STRUCTURILOR SI
ELEMENTE DE INGINERIE SEISMICA
Dinamica sistemelor cu 1 GLD.
Vibratii fortate amortizate produse de actiunile armonice
In ecuatia de echilibru dinamic
instantaneu care va caracteriza miscarea sistemului, intervin urmatoarele
forte: (i) forta de inertie, ![]() ; (ii) forta de amortizare,
; (ii) forta de amortizare, ![]() ; (iii) forta elastica,
; (iii) forta elastica, ![]() ; si (iv) forta perturbatoare
; si (iv) forta perturbatoare ![]() . In continuare se va considera
. In continuare se va considera ![]() armonica avand forma
armonica avand forma ![]() .
.
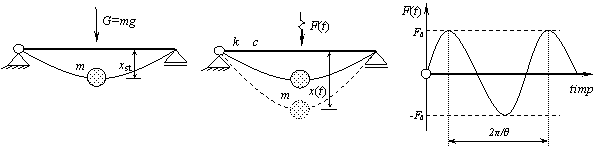
Ecuatia de miscare a sistemului dinamic rezulta de forma:
![]()
Solutia acestei ecuatii diferentiale de
ordinul II cu coeficienti constanti este de forma ![]() unde:
unde:
![]() reprezinta solutia
ecuatiei omogene, care corespunde vibratiilor libere cu amortizare si care are
forma deja cunoscuta
reprezinta solutia
ecuatiei omogene, care corespunde vibratiilor libere cu amortizare si care are
forma deja cunoscuta ![]() adica se poate scrie
expresia
adica se poate scrie
expresia ![]() sau
sau ![]() ;
;
Constantele M si N se determina din conditia ca aceasta solutie sa satisfaca ecuatia miscarii:
![]()
![]()
Prin identificarea coeficientilor functiilor trigonometrice rezulta urmatorul sistem de ecuatii:
![]() si
si ![]()
![]()
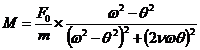
![]()
![]()
Deoarece ![]() reprezinta o
suprapunere a doua oscilatii armonice de
aceeasi pulsatie, aceasta se mai poate scrie sub forma:
reprezinta o
suprapunere a doua oscilatii armonice de
aceeasi pulsatie, aceasta se mai poate scrie sub forma:
![]() unde
unde ![]() si
si ![]()
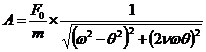
![]()
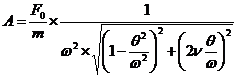 sau
sau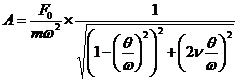 dar
dar![]()
![]()
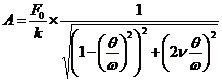 sau
sau ![]() unde
unde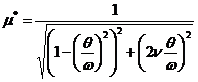
![]()
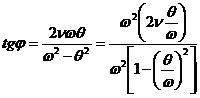
![]()
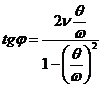
![]() reprezinta
coeficientul dinamic sau factorul de amplificare dinamica cand se tine seama de
prezenta amortizarii. Este evident ca atunci cand se face abstractie de
amortizare, adica
reprezinta
coeficientul dinamic sau factorul de amplificare dinamica cand se tine seama de
prezenta amortizarii. Este evident ca atunci cand se face abstractie de
amortizare, adica ![]() , rezulta
, rezulta ![]() . In aceste conditii raspunsul fortat, exprimat prin
deplasari relative, devine
. In aceste conditii raspunsul fortat, exprimat prin
deplasari relative, devine ![]() , iar raspunsul total exprimat tot prin deplasari relative
are forma:
, iar raspunsul total exprimat tot prin deplasari relative
are forma:
![]()
Se va evalua raspunsul total considerand
urmatoarele conditii initiale: ![]()
![]()
![]() si
si ![]() . Pentru determinarea constantelor
. Pentru determinarea constantelor ![]() si
si ![]() este mai convenabil sa
se scrie astfel:
este mai convenabil sa
se scrie astfel:
![]()
![]()
Introducand conditiile initiale in ecuatiile de mai sus se obtin cele doua constante:
![]()
![]()
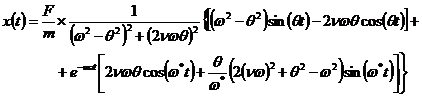
Daca se imparte numitorul si numaratorul
la ![]() relatia de mai sus se
transforma astfel:
relatia de mai sus se
transforma astfel:
sau: unde
![]()
![]() reprezinta factorul de amplificare dinamica variabil in timp.
reprezinta factorul de amplificare dinamica variabil in timp. ![]() are caracterul
unei functii de transfer, in sensul ca transfera actiunea in raspuns.
are caracterul
unei functii de transfer, in sensul ca transfera actiunea in raspuns.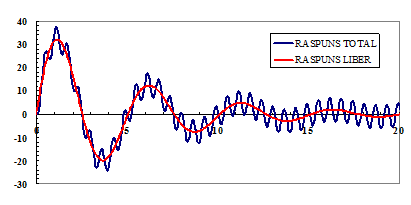
|
Politica de confidentialitate |
| Copyright ©
2026 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |