
Stiva
Stiva este acea forma de organizare a datelor cu propietatea ca operatiile de introducere si scoatere a datelor se fac in varful ei.
Stivele se pot simula cu ajutorul vectorilor. Daca ST este un vector de dimensiune n, atunci in elementele acestuia ST[1], ST[2], , ST[n] se pot retine litere sau cifre.
Varful stivei poate fi indicat de catre o variabila intreaga k:
|
B | ||||||
A |
A |
A | ||||
|
k |
k |
k |
k |
La scoaterea unei variabile din stiva, variabila k scade cu o unitate
La introducerea unei variabile in stiva, variabila k creste cu o unitate.
Cand k = 0, stiva este vida.
Pentru x natural, se cere sa se intocmeasca algoritmul care permite determinarea valorilor functiei
![]()
x - 1 ,daca x >= 12;
f x) =
f ( f ( x +2)) ,in caz contrar.
Dupa cum se constata, functia este definita recursiv. De exemplu, daca x 15, se obtine imediat f Pentru x 8, rezultatul se obtine dupa mai multi pasi
f ) = f f ) ) = f f f ) ) ) = f f ) ) = f f f ) ) ) =
= f f ) ) = f ) = f f ) ) = f ) = 11.
Utilizand o stiva ST si o variabila k ce indica varful stivei, problema poate fi rezolvata astfel:
Se asociaza nivelului k al stivei apelarea de k ori a functiei f (apelarea lui f x) se asociaza lui k apelarea lui f f x)) se asociaza lui k apelarea lui f f f x))) se asociaza lui k=3 etc.), iar pe nivelul k al stivei se pune valoarea curenta a lui x
La fiecare apelare a functiei f se urca in stiva k se creste cu o unitate), iar pe nivelul respectiv se pune noua valoare a lui x;
Cand, pentru o valoare a lui k, se poate calcula valoarea functiei, atunci se coboara in stiva, iar pe noul nivel se pune valoarea calculata;
Calculul se incheie cand k =0, valoarea functiei fiind ST
Modul de functionare al algoritmului, pentru calculul lui f ) este ilustrat in continuare:
|
| ||||||||
|
k |
k |
k |
k |
k |
||||
|
k |
k |
k |
k |
k |
Rezulta, f(8) = ST[1] - 1 = 11.
/* MANNA PNUELI */
#include <stdio.h>
#include <conio.h>
void main(void)
else
for(i=0;i<k;)printf('%3d',stiva[++i]);
printf('n');
}
printf('f(%d)=%d',x,stiva[1]-1);
getch();
}
Se considera functia f N x N -> N, definita astfel
![]()
n+1 , daca m = 0;
f m,n) = f ( m -1, 1) , daca n = 0;
f ( m -1, f (m, n -1)) , daca mn <> 0.
Pentru m si n date, se cere sa se intocmeasca algoritmul care permite calculul valorilor functiei.
Exemplu
f ) = f f ) ) = f f ) ) = f f f ) ) ) =
= f f f ) ) ) = f f ) ) = f ) = f f ) ) =
= f f f ) ) ) = f f f f ) ) ) ) =
= f f f f ) ) ) ) = f f f ) ) ) =
= f f ) ) = f ) = 5.
Pentru calculul valorilor functiei, se va folosi o stiva dubla, ST
Initial, pe nivelul 1 al stivei, se retin valorile m si n
Pe nivelul k al stivei, se retin valorile curente m si n
Functie de valorile variabilelor m si n, se procedeaza dupa cum urmeaza
a) Pentru m <> 0 si n <> 0, este necesara o apelare recursiva a functiei, deci se urca in stiva, iar pe noul nivel se pun valorile m si n
b) Pentru n = 0, se ramane pe acelat nivel, dar in locul lui m se pune valoarea m -1, iar in locul lui n se pune valoarea
c) Pentru m = 0, functia se poate calcula. Se oboara un nivel in stiva si, pe noul nivel, valoarea lui m se inlocuieste cu m - 1, iar valoarea lui n se inlocuieste cu valoarea de pe nivelul anterior, marita cu o unitate
Functionarea algoritmului, pentru f(2, 1), este ilustrata in continuare :
|
| ||||||||||||
Rezulta, f (2, 1) = f (0, 4) = 5.
/* ACKERMANN */
#include <stdio.h>
#include <conio.h>
void main(void)
else if (!(stiva[k][2]))
else
}
}
printf('f(%d,%d)=%d',m,n,stiva[1][2]+1);
getch();
}
3. METODA BACKTRACKING
Fiind date multimile finite: A , A ,., An, ale caror elemente se afla intr o relatie de ordine bine stabilita, metoda backtraking permite determinarea solutiilor de tip vector S = ( x , x ,., xn), unde x I A x I A xn I An
Metoda backtraking se recomanda a se utiliza atunci cand rezolvarea unei probleme nu se poate face printr o alta metoda mai rapida.
Observatii
In multe situatii multimile: A , A ,., An coincid.
Deoarece solutiile unei probleme, rezolvate prin metoda backtraking, sunt elemente ale produsului cartezian A x A x . x An, aceasta poate fi rezolvata si prin generarea tuturor elementelor produsului cartezian cu selectarea numai a acelor solutii care verifica conditiile problemei. Rezolvarea problemei in acest mod necesita un timp foarte mare.
Metoda backtraking consta in urmatoarele
Se alege x ,primul element din multimea A
Presupunand ca s-au ales elementele x , x ,., xk, apartinand multimilor A , A ,., Ak, se alege xk+ , primul element disponibil din multimea Ak
a) daca elementul xk+ exista, adica verifica conditiile de continuare a calcului, se verifica daca nu s-a obtinut o solutie. In caz afirmativ, se tipareste solutia sau, in caz contrar, se considera generate elementele x , x ,., xk, xk+
b) daca elementul xk+ nu exista, se considera generate elementele x , x ,., xk si se cauta un nou element xk, in multimea Ak
Algoritmul se incheie cand au fost luate in considerare toate elementele multimii A
|
xk | |
|
x | |
|
x | |
|
ST |
Implementarea metodei backtraking se poate face utilizand structura de stiva ST in care, pe nivelele 1, 2,, k, se depun elementele x , x ,., xk
Gasirea elementului xk+ determina urcarea in stiva pe nivelul k+1. In caz contrar, se coboara pe nivelul k -1.
Cand se atinge nivelul zero, algoritmul se incheie.
Observatii
a) La urcarea in stiva, pe nivelul atins, initial se pune o valoare care nu apartine multimii asociate nivelului. Aceasta valoare este apoi inlocuita cu primul element valid din multimea respectiva.
b) Cand este validat un element de pe nivelul n, inseamna ca s-a obtinut o solutie.
Se considera o tabla de sah, de dimensiune n x n. Se cere sa se determine solutiile de aranjare a celor n dame, astfel incat sa nu se atace reciproc, adica sa nu existe doua dame situate pe aceeasi linie, coloana sau diagonala).
Exemplu: Pentru n=4, o solutie ar fi urmatoarea:
|
D | |||
|
D |
|||
|
D | |||
|
D |
Solutia poate fi determinata astfel:
- Se pune prima dama pe linia 1, coloana 1 (fig. 3.1.a);
|
D |
D |
D |
D | |||||||||||||||||||
|
D |
D |
D |
||||||||||||||||||||
|
D |
| |||||||||||||||||||||
|
|
a) b) c) d)
Fig. 3.1.
- A doua dama se poate plasa pe linia 2, coloana 3 (fig. 3.1.b). A treia dama nu mai poate fi plasata in linia 3;
- Se pune a doua dama in linia 2, coloana 4 (fig. 3.1.c);
- A treia dama se poate plasa pe linia 3, coloana 2 (fig. 3.1.d). In aceasta situatie, a treia dama nu mai poate fi plasata pe linia 4;
- Cum dama 2 nu poate avansa, prima dama se plaseaza in coloana 2 (fig. 3.a);
- A doua dama nu poate fi plasata decat pe linia 2, coloana 4 (fig. 3.b);
- Dama 3 nu poate fi plasata decat pe linia 3, coloana 1 (fig. 3.c);
- A patra dama poate fi plasata in coloana 3.
Se obtine solutia din fig. 3.d.
|
D |
D |
D |
D | ||||||||||||||||||
|
D |
D |
D |
|||||||||||||||||||
|
D |
D | ||||||||||||||||||||
|
D |
a) b) c) d)
Fig. 3.
Determinarea solutiilor se poate face utilizand o stiva ST, cu n componente, unde, atunci cand dama i se gaseste pe coloana k, pe nivelul i se pune valoarea k, adica ST(i) = k.
Doua dame oarecare nu se ataca reciproc, daca, pentru i, j I, i j sunt indeplinite conditiile: ST(i) ST(j) si ST(i) - ST(j) i - j
Conform algoritmului backtracking, rezulta:
|
ST(1) = ST(2) |
ST(1) - ST(2) | |||||
|
|
Nu convine. |
Nu convine. |
|
ST(1) = ST(3) |
ST(2) - ST(3) |
ST(2) = ST(3) |
|||
|
Nu convine. |
Nu convine. |
|
Nu convine. |
|
ST(3) - ST(2) |
ST(1) = ST(3) | |||||
|
Nu convine. |
Nu convine. |
|
ST(1) =ST(4) |
ST(4) - ST(3) |
ST(4) = ST(2) |
|||
|
|
Nu convine. |
Nu convine. |
Nu convine. |
|
ST(2) - ST(3) |
ST(3) = ST(2) | ||||
|
|
Nu convine. |
Nu convine. |
etc. |
/* DAME */
#include <stdio.h>
#include <stdlib.h>
#include <conio.h>
void init_nivel(int k, int stiva[])
int cauta_succesor(int k, int stiva[], int n)
return exista_succesor;
}
int validare_succesor(int k, int stiva[])
return valid;
}
int obtinut_solutie( int k, int n)
void afiseaza(int a[], int k)
void main(void)
while (!((exista_succesor&&succesor_valid)||
(!exista_succesor)));
if (exista_succesor)
;
}
else k--;
}
getch();
}
Pentru un numar natural n, se cere sa se genereze toate permutarile multimii . De exemplu, pentru n=3, utilizand stiva ST, rezulta:
|
ST(1) = ST(2) |
ST(1) = ST(3) |
||||||
|
|
Nu convine. |
Nu convine. |
|
ST(2) = ST(3) |
ST(1) = ST(3) |
||||||
|
Nu convine. |
|
Nu convine etc. |
Se constata ca se poate utiliza algoritmul dame, cu observatia ca, la validare, se verifica numai daca, pe doua niveluri diferite, valorile sunt diferite.
/* PERMUTARI de n*/
/*numai modificarile fata de DAME */
int validare_succesor(int k, int stiva[])
return valid;
}
Pentru numerele naturale n si p, se cere sa se genereze toate sbmultimile de p elemente ale multimii . Doua submultimi pot sa difere prin ordinea sau prin natura elementelor.
Din analiza problemei, rezulta urmatoarele:
Stiva trebuie sa aiba inaltimea p;
Fiecare nivel ia valori intre 1 si n;
Elementele plasate pe niveluri diferite trebuie sa fie distincte.
Se constata ca se poate utiliza algoritmul permutari cu observatia ca stiva are inaltimea p.
/* ARANJAMENTE din n luate cate p */
/*numai modificarile fata de permutari din n */
void main(void)
,
![]()
1 , daca exista drum intre orasele i si j;
a i, j] =
0 , in caz contrar.
Deoarece daca exista drum intre orasele i si j, atunci exista drum si intre orasele j si i, rezulta ca matricea A este simetrica, adica a i, j] = a[j, i]
Exemplu: Daca, pentru n = 6, drumurile existente intre cele 6 orase sunt reprezentate in figura urmatoare:
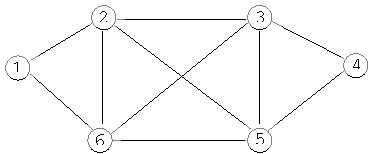
rezulta urmatoarea matrice
|
A | |||||||
Pentru rezolvarea problemei, se foloseste o stiva ST. Pe fiecare nivel al stivei, se incarca cifra corespunzatoare unui oras, pe nivelul 1 fiind incarcata cifra orasului de plecare. Un succesor, intre 2 si n, este evident valid daca:
a) nu se gaseste in stiva, adica nu s-a mai trecut prin acel oras;
b) exista un drum intre orasul situat pe nivelul k si orasul situat pe nivelul k-1;
c) daca succesorul este situat pe nivelul n, atunci trebuie sa existe un drum de la acesta la orasul aflat pe nivelul 1.
/* COMIS-VOIAJOR */
#include <stdio.h>
#include <stdlib.h>
#include <conio.h>
void init_nivel(int k, int stiva[])
int cauta_succesor(int k, int stiva[], int n)
return exista_succesor;
}
int validare_succesor(int k, int stiva[],
int a[][10], int n)
if ((k==n)&&(a[1][stiva[k]]==0)) valid=0;
return valid;
}
int obtinut_solutie( int k, int n)
void afiseaza(int a[], int k)
void main(void)
k=1;
init_nivel(k, stiva);
init_nivel(++k, stiva);
while (k>1)
while (!((exista_succesor&&succesor_valid)||
(!exista_succesor)));
if (exista_succesor)
if (obtinut_solutie( k, n))
afiseaza( stiva, k);
else init_nivel( ++k, stiva);
else k--;
}
getch();
}
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |