PROCESUL DE MASURARE
Procesul de masurare reprezinta ansamblul operatiilor experimentale efectuate in scopul determinarii cantitative a unei marimi. Orice proces de masurare contine urmatoarele elemente principale:
- masurandul (marimea de masurat);
- etalonul;
- metoda de masurare;
- aparatul de masurat.
In functie de natura, precizia si scopul masurarii, aceste elemente au o importanta relativa diferita. Ele determina marea varietate a masurarilor. Oricare dintre aceste elemente ale procesului de masurare poate servi ca punct de plecare intr-o clasificare a masurarilor.
1.1. Masurandul. Unitati de masura. Marimi si unitati fundamentale
In ultima instanta, procesul de masurare consta in compararea actiunii marimii de masurat, x, sau a mijlocului de masurare asupra obiectului supus masurarii, cu actiunea de acelasi fel a unei marimi x , luata drept referinta.
Marimea de referinta care intervine in procesul de masurare este materializata sub forma unui obiect numit masura, care, printr-una din proprietatile sale, reproduce una sau mai multe valori ale marimii respective. Pentru cunoasterea valorii masurii, ea trebuie, la randul ei, sa fie masurata cu un mijloc de masurare etalon. Cu alte cuvinte, elementul de baza pentru realizarea procesului de masurare il constituie stabilirea unui sistem de unitati de masura.
Ansamblul unitatilor de masura definite pentru un sistem dat de marimi fizice formeaza un sistem de unitati de masura.
In decursul dezvoltarii fizicii au fost utilizate si inca se mai utilizeaza mai multe sisteme de unitati de masura. Practica folosirii acestora a aratat ca un sistem de unitati trebuie sa indeplineasca urmatoarele conditii:
-sa fie general, adica aplicabil tuturor capitolelor fizicii;
-sa fie coerent, adica sa nu introduca coeficienti numerici suplimentari in ecuatiile fizicii;
-sa fie practic, in sensul ca unitatile din sistem sa aiba, pe cat posibil, ordine de marime comparabile cu valorile uzuale in activitatea umana.
Conditiile expuse sunt indeplinite cel mai bine de catre Sistemul International de Unitati (SI), adoptat in anul 1960 la cea de-a XI-a Conferinta Generala de Masuri si Greutati (CGPM), impreuna cu denumirile si simbolurile unitatilor.
In prezent SI este in curs de generalizare in intreaga lume. In Romania el a fost adoptat in anul 1961 ca sistem de unitati de masura unic, legal si obligatoriu.
In SI se disting trei clase de unitati: unitati fundamentale, unitati derivate si unitati suplimentare. Aceasta clasificare, desi nu este impusa univoc de legile fizicii, a fost gasita avantajoasa pentru activitatea practica din diferite domenii.
S-a convenit ca SI sa aiba la baza sapte unitati fundamentale, considerate independente din punct de vedere dimensional: metrul, kilogramul, secunda, amperul, kelvinul, molul si candela.
A doua clasa de unitati cuprinde unitati derivate, care pot fi deduse combinand unitatile fundamentale pe baza unor ecuatii ale fizicii in care intervin marimile corespunzatoare. In principiu, numarul unitatilor derivate nu este limitat. O parte din unitatile derivate au denumiri speciale, care pot fi folosite pentru formarea altor unitati derivate (de exemplu: 1N=1kg*m*s- si 1Pa=1N*m- ). A treia clasa de unitati SI include doua unitati suplimentare: radianul si steradianul.
Definitiile unitatilor fundamentale ale SI au cunoscut mai multe modificari in decursul timpului, generate de nevoia mereu crescanda de imbunatatire a preciziei masurarilor. Un exemplu semnificativ in acest sens il constituie metrul, aflat acum la a cincea definitie (a se vedea mai jos). Un alt exemplu, insa in celalalt sens (stabilitate), il constituie kilogramul, a carui definitie a ramas neschimbata din anul 1889.
In legatura cu definitiile unitatilor SI fundamentale se impun urmatoarele precizari :
1). Definitiile trebuie sa fie clare, precise si stiintifice. De asemenea, ele trebuie sa fie suficient de simple pentru a putea fi intelese si de oameni fara pregatire deosebita si, in acelasi timp, sa fie lipsite de ambiguitati pentru specialisti.
2). Scopul unei definitii nu este acela de a stabili reguli practice de punere a ei in aplicare. Aceasta sarcina revine Comitetului International de Masuri si Greutati (CIPM) care, cu sprijinul diferitelor comitete consultative create in acest scop (a se vedea si subcapitolul 5.7), elaboreaza recomandari internationale privind materializarea definitiilor prin experimente adecvate.
3). Definitiile sunt adoptate prin rezolutii ale Conferintei Generale de Masuri si Greutati, care au la baza studii efectuate de comitetele consultative.
In continuare se prezinta actualele definitii ale unitatilor SI fundamentale, impreuna cu anumite observatii referitoare la ele.
Metrul este lungimea drumului parcurs de lumina in vid in timpul de 1/299 792 458 s.
Aceasta definitie, adoptata de cea de-a XVII-a Conferinta Generala de Masuri si Greutati in 1983, este a cincea definitie oficiala a metrului, dupa cele din 1799, 1872, 1889 si 1960. Definitia din 1889 era bazata pe un prototip international iar cea din 1960 pe lungimea de unda a uneia din radiatiile atomului de kripton 86. Actuala definitie a metrului nu le contrazice pe cele precedente dar asigura o reproductibilitate mai buna a etaloanelor corespunzatoare. O data cu aceasta definitie se adopta pentru viteza luminii in vid valoarea conventionala c=299 792 458 m/s, considerata exacta. In acest mod c devine o constanta fizica universala.
Kilogramul este egal cu masa prototipului international al kilogramului.
Acest prototip, realizat din aliaj de platina si iridiu, se pastreaza la sediul Biroului International de Masuri si Greutati (BIPM) de la Sevres, Franta, in conditiile stabilite de prima Conferinta Generala de Masuri si Greutati in 1889.
Secunda este durata a 9 192 631 770 perioade ale radiatiei care corespunde tranzitiei intre cele doua niveluri hiperfine ale starii fundamentale a atomului de cesiu 133.
Amperul este intensitatea unui curent constant care, mentinut in doua conductoare paralele, rectilinii, cu lungimea infinita si cu sectiunea circulara neglijabila, asezate in vid la o distanta de 1 m unul de altul, produce intre aceste conductoare o forta de 2*10- N pe o lungime de 1 m.
Aceasta definitie este echivalenta cu stabilirea unei valori conventionale de 4 H/m pentru permeabilitatea vidului,
Kelvinul, unitatea de temperatura termodinamica, este fractiunea 1/273,16 din temperatura termodinamica a punctului triplu al apei.
Molul este cantitatea de substanta a unui sistem care contine atatea entitati elementare cati atomi exista in 0,012 kg de carbon 12.
La utilizarea molului astfel definit, entitatile elementare trebuie specificate, ele putand fi atomi, molecule, ioni, electroni, alte particule sau grupuri de particule.
Candela este intensitatea luminoasa, intr-o directie data, a unei surse care emite o radiatie monocromatica cu frecventa de 540*10 Hz si a carei intensitate energetica in aceasta directie este de 1/683 W/sr.
Aceasta definitie, bazata pe masurarea fluxului energetic al radiatiilor optice prin mijloace radiometrice a fost adoptata in 1979 (la a XVI-a CGPM). Ea o inlocuieste pe cea precedenta, bazata pe radiatorul lui Planck (corpul negru) si pe mijloace fotometrice.
Se remarca trei modalitati de definire a unitatilor fundamentale: pe baza de prototipuri, pe baza de proprietati macroscopice ale unor materiale si pe baza de proprietati atomice, cu tendinta de crestere a numarului de unitati definite atomic.
1.2. Etalonul
Etalonul este prezent - direct sau indirect - la fiecare masurare efectuata cu un mijloc de masurare. Diferitele categorii de etaloane sunt tratate in capitolul 2.
1.3. Metoda de masurare
Orice masurare este o comparatie a masurandului cu un etalon. Prezenta etalonului, chiar daca uneori ea este mai putin evidenta, este indispensabila.
Deosebim
masurari prin comparatie
simultana si masurari prin comparatie succesiva. La comparatia simultana
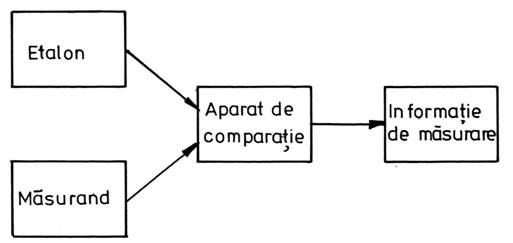
(fig. 1.1) masurandul este comparat nemijlocit cu o marime de
referinta de aceeasi natura (de exemplu, masurarea unei mase prin compararea cu o masa
etalon cu ajutorul unei balante cu brate egale).
Fig. 1.1. Metoda de masurare prin comparatie simultana.
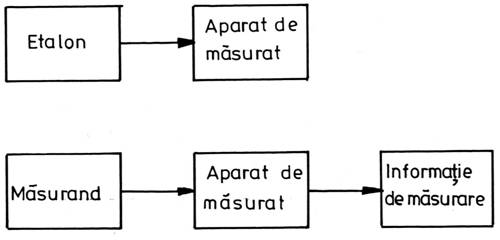
La comparatia succesiva (fig. 1.2) marimea de referinta (etalon) nu participa direct la fiecare masurare. Ea serveste pentru calibrarea initiala a unui aparat de masurat care pastreaza in 'memoria' sa informatia de calibrare; aceasta informatie, primita initial de la etalon este apoi transmisa de aparat cu ocazia fiecarei masurari ulterioare (aparatul de masurat este recalibrat periodic, insa - in contextul prezentei clasificari - procesul de recalibrare poate fi asimilat cu o calibrare initiala).
Exemple de masurari prin comparatie succesiva sunt: masurarea unei mase cu un cantar cu scara gradata, masurarea tensiunii cu voltmetrul, masurarea curentului cu ampermetrul etc.
Este interesant de remarcat ca, istoric, metodele de comparatie simultana au fost primele care au aparut (pentru masurari de lungime, volum, masa). Mai tarziu, o data cu progresele tehnologice, masurarea prin comparatie succesiva a devenit mai raspandita. Totusi, comparatia simultana este predominanta - si deseori singura utilizata - in masurarile de cea mai inalta precizie, proprii laboratoarelor de metrologie, cum sunt: compararea cu mare precizie a maselor, masurarea lungimii folosind radiatii etalon, masurarea tensiunii prin comparatii cu etaloane de tensiune si rezistenta, masurari de temperatura folosind punctele fixe ale Scarii Internationale Practice de Temperatura etc.
In cazul masurarilor prin comparatie simultana, masurandul poate fi comparat fie cu un etalon de valoare apropiata sau egala, fie cu un etalon de valoare diferita. Cele doua categorii de comparatii pot fi denumite comparatie 1:1, respectiv comparatie 1:n. La randul lor, ele pot fi impartite in subcategorii:
|
directa |
||
|
Comparatie 1:1 |
simpla |
|
|
Comparatie |
indirecta prin substitutie |
|
|
simultana |
prin permutare |
|
|
prin metode de aditionare |
||
|
Comparatie 1:n | ||
|
prin metode de raport |
In principiu, orice masurare prin comparatie simultana se poate face printr-o metoda diferentiala sau printr-o metoda de zero.
1.3.1. Comparatia 1:1 directa
Comparatia 1:1 directa poate fi aplicata numai marimilor fizice care au polaritate, cum sunt lungimea, forta, presiunea, tensiunea electrica etc. Ea se poate face prin metoda diferentiala sau prin metoda de zero.
a). Metoda diferentiala directa consta in masurarea nemijlocita a diferentei dintre masurand si o marime de referinta cunoscuta, de valoare apropiata de cea a masurandului :
x = x + d (1.1)
unde
x este valoarea masurandului,
x - valoarea de referinta cunoscuta
d - diferenta masurata direct.
Un exemplu de masurare diferentiala directa este redat in fig. 1.3. Tensiunea Ux a sursei necunoscute rezulta din valoarea de referinta U (cunoscuta cu precizie) si diferenta u masurata direct, Ux = U + u.
|
|
Avantajul metodei consta in aceea ca daca diferenta d este suficient de mica in raport cu x, incertitudinea aferenta lui d poate fi neglijata, iar incertitudinea rezultatului este practic egala cu incertitudinea lui x (a se vedea si problema 1.5.1). |
Fig. 1.3. Metoda diferentiala.
Intr-adevar, presupunand ca x si d variaza cu x si respectiv cu d, variatia corespunzatoare a lui x este
x = x d . (1.2)
Impartind aceasta egalitate cu x, se obtine
![]() . (1.3)
. (1.3)
Intrucat x este apropiat de x , in primul termen din membrul drept x poate fi inlocuit prin x . Inmultind ultimul termen cu d/d, rezulta
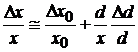 . (1.4)
. (1.4)
In aceasta relatie, termenul x/x poate fi interpretat ca incertitudine relativa a lui x, x /x ca incertitudine relativa a marimii de referinta, iar d/d ca incertitudine relativa a diferentei d masurate direct. Daca d este suficient de mic in comparatie cu x, rezulta
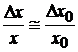
b). Metoda de zero directa este un caz particular al metodei diferentiale, in care diferenta dintre masurand si marimea de referinta este adusa la zero
x = x (1.6)
Se observa ca in acest caz aparatul nu mai masoara propriu-zis, el fiind folosit doar ca indicator de nul. Ca urmare, influenta sa asupra incertitudinii de masurare este si mai mica decat in cazul metodei diferentiale. Din relatia (1.6) nu trebuie insa sa se traga concluzia ca aparatul de masurat nu introduce nici o incertitudine de masurare. Egalitatea (1.6) este valabila in limitele pragului de sensibilitate al aparatului folosit ca indicator de nul, prag notat mai jos cu ui:
x=x ui. (1.7)
Ca urmare, incertitudinea relativa a masurarii este
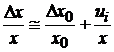
O alta sursa de incertitudine apare din imposibilitatea reglarii marimii x in trepte suficient de fine. In practica se intampla frecvent ca indicatia zero sa nici nu poata fi obtinuta cu exactitate; in astfel de cazuri se cauta sa se obtina doua deviatii ale indicatorului de nul, de o parte si de alta a reperului zero, iar apoi se face o interpolare.
Metoda diferentiala directa si metoda de zero directa sunt in general cele mai precise metode de masurare deoarece incertitudinea introdusa de aparatul de masurat este minima. Ele au insa dezavantajul ca necesita un etalon de valoare apropiata de valoarea masurandului sau un etalon de valoare variabila.
1.3.2. Comparatia 1:1 indirecta
Comparatia 1:1 indirecta utilizeaza un aparat intermediar de comparatie. Ea se aplica mai ales in cazul marimilor fizice fara polaritate (masa, rezistenta electrica, capacitate etc.) dar poate fi utilizata in general pentru masurarea oricaror categorii de marimi. Cele mai cunoscute exemple de masurari prin comparatie 1:1 indirecta sunt: compararea maselor cu ajutorul unei balante cu brate egale si compararea impedantelor electrice de aceeasi natura (rezistente intre ele, capacitati intre ele, inductante intre ele etc.) cu ajutorul unei punti de masurare cu brate egale.
Comparatia 1:1 indirecta se poate face prin metoda comparatiei simple, metoda substitutiei sau metoda permutarii.
1). Metoda comparatiei 1:1 indirecte simple consta in compararea celor doua marimi - masurandul si referinta - cu ajutorul unui aparat numit comparator 1:1.
Rezultatul masurarii este dat de relatia
x = Kx (1.9)
unde K este un factor introdus de comparator, avand aproximativ valoarea 1. Acest factor este o importanta sursa de incertitudine in procesul de masurare, atat in cazul in care se ia K =1 (si in realitate K=1+, unde este o corectie neaplicata), cat si in cazul corectarii lui K, introducand in relatia (1.9) valoarea sa reala (datorita incertitudinii cu care se cunoaste corectia
Masurarea propriu-zisa cu comparatorul poate fi efectuata printr-o metoda diferentiala sau printr-o metoda de zero. In acest caz este judicios ca ele sa fie numite metoda diferentiala indirecta si respectiv metoda de zero indirecta. Exista o deosebire clara intre aceste metode si metodele directe corespunzatoare. Pentru relevarea acesteia, sa presupunem in continuare ca indicatoarele de nul sunt ideale (nu introduc erori). In acest caz, la metoda de zero directa echilibrarea la zero in procesul de masurare conduce neconditionat la egalitatea x=x . De exemplu, indicatia zero a indicatorului de nul la compararea a doua tensiuni in opozitie implica egalitatea lor. La metoda de zero indirecta conditia de nul in sine nu este echivalenta cu egalitatea marimilor comparate. De exemplu, o punte-comparator de rezistenta, aflata la echilibru, nu implica in mod necesar egalitatea rezistentelor deoarece raportul bratelor puntii poate sa fie diferit de 1.
Exemple de aparate care masoara prin metoda diferentiala indirecta sunt: balanta semiautomata cu cadran si greutati, puntea tensometrica neechilibrata etc.
Exemple de aparate care masoara prin metoda de zero indirecta sunt: balanta cu brate egale, echilibrata, puntea Wheatstone cu brate egale etc.
2). Metoda substitutiei, denumita si metoda Borda sau metoda efectelor egale, elimina eroarea sistematica a comparatorului printr-o masurare dubla. Cele doua marimi de comparat se aplica succesiv aparatului, egalitatea lor fiind semnalata de faptul ca au acelasi efect asupra aparatului. In acest fel, eroarea lui este eliminata deoarece ea intervine la fel in ambele masurari.
Practic, comparatorul folosit in acest scop are raportul stabil dar nu neaparat egal cu 1. Sensibilitatea comparatorului este cea care determina, in primul rand, precizia masurarii.
Metoda substitutiei poate fi ilustrata prin compararea a doua mase cu ajutorul unei balante cu brate egale (fig. 1.4 b). Pe langa masele de comparat (masa necunoscuta x si masa etalon x ) mai este necesara o masa auxiliara xt, numita tara, de valoare apropiata de x si de x . La prima masurare se pune pe un platan al balantei masa x, iar pe celalalt platan masa xt. Variind pe xt se ajunge la echilibrul balantei. Daca lungimile bratelor balantei sunt l si l , se poate scrie relatia:
l x = l xt (1.10)
La a doua masurare se pune masa x in locul masei x, pe celalalt platan ramanand masa xt, nemodificata. Se reechilibreaza balanta prin modificarea lui x . Rezulta
l x = l xt (1.11)
unde cu x s-a notat valoarea care asigura echilibrul.
Din relatiile (1.10) si (1.11) rezulta
x = x
Rezultatul nu depinde nici de raportul bratelor l /l nici de masa auxiliara xt. Prin faptul ca exclude influenta erorilor sistematice ale balantei, metoda se aplica in masurarile de cea mai inalta precizie. Incertitudinea masurarii va depinde, in principal, de sensibilitatea balantei si de erorile aleatoare. In mod asemanator decurge masurarea unei rezistente, a unei capacitati sau a unei inductante prin metoda substitutiei, folosind o punte‑comparator ca aparat de comparatie.
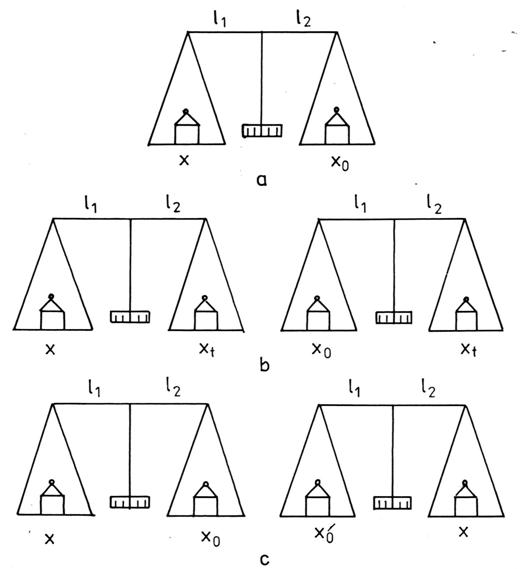
Fig. 1.4. Metode de masurare a maselor prin comparatie 1:1 indirecta:
a). comparatie simpla; b). metoda substitutiei; c). metoda permutarii.
De observat ca, in exemplul dat, echilibrarea la zero in cele doua masurari se obtine prin modificarea marimilor xt si x (tara si referinta). In multe cazuri, mai ales in masurarile electrice, marimile xt si x sunt mentinute neschimbate si se modifica, in limite restranse, raportul comparatorului. In acest caz, relatia (1.10) poate fi scrisa sub forma
x = (K+k )xt (1.13)
unde K este raportul comparatorului, iar k este o mica variatie data lui K pentru echilibrarea comparatorului.
La a doua masurare se obtine
x = (K+k )xt (1.14)
unde k este noua variatie a lui K pentru echilibrarea comparatorului.
Prin impartirea relatiilor (1.13) si (1.14), membru cu membru, rezulta
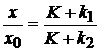 . (1.15)
. (1.15)
In situatia in care k si k sunt mult mai mici decat K (ceea ce se intampla practic la toate comparatiile 1:1 de precizie ridicata), relatia (1.15) poate fi adusa la forma
![]() . (1.16)
. (1.16)
Daca x este apropiat de x , termenul de corectie k -k este mic fata de 1 si eroarea introdusa de comparator este neglijabila. In practica se iau precautii speciale pentru ca variatiile lui k si k sa pastreze mici erorile termenului de corectie. Astfel, atunci cand raportul K poate fi variat in decade (de exemplu, cu ajutorul unui rezistor in decade sau al unui divizor inductiv in decade), o regula bine cunoscuta cere ca variatiile k si k sa fie realizate numai prin modificarea ultimelor decade, primele decade ramanand pe aceleasi pozitii in cele doua masurari succesive. Pentru aceasta, primele decade vor fi puse la inceput pe pozitiile 9; 9; 9; si nu pe 10; 0; 0; deoarece in al doilea caz raportul K nu va putea lua valori subunitare fara trecerea primei decade de pe 10 pe 9 (a se vedea si problema 1.5.2).
3). Metoda permutarii, denumita si metoda Gauss sau metoda transpozitiei, reprezinta o alta posibilitate de eliminare a erorii comparatorului in cazul unei comparatii 1:1. Se fac si in acest caz doua masurari succesive. Caracteristica pentru aceasta metoda este schimbarea intre ele a marimilor comparate, de la prima la a doua masurare, ceea ce face ca erorile comparatorului sa afecteze, pe rand, in egala masura cele doua marimi.
Pentru ilustrarea acestei metode, se va considera tot compararea a doua mase cu ajutorul unei balante cu brate egale (fig. 1.4 c). La prima masurare se pune masa x pe un platan si masa x pe celalalt platan. Rezulta
l x = l x
La a doua masurare se schimba intre ele locurile lui x si x Daca l l , va fi necesara o modificare a masei etalon x pentru echilibrarea balantei. Fie x valoarea care realizeaza aceasta. Se poate scrie
l x = l x (1.18)
Din relatiile (1.17) si (1.18) rezulta
![]() (1.19)
(1.19)
Relatia (1.19) evidentiaza faptul ca si in cazul metodei Gauss rezultatul masurarii este independent de raportul lungimilor bratelor l /l
Daca echilibrarea s-ar face prin varierea raportului K al comparatorului, relatiile corespunzatoare celor doua masurari ar putea fi scrise astfel:
x = (K+k )x
si
x = (K+k )x, (1.21)
unde k si k sunt variatiile date lui k pentru echilibrarea comparatorului.
Din relatiile (1.20) si (1.21) rezulta
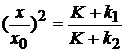 (1.22)
(1.22)
din care, tinand cont ca atat k cat si k sunt mici fata de K, rezulta succesiv:
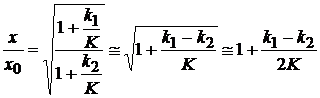 (1.23)
(1.23)
sau, inlocuind K=1 in termenul de corectie (unde abaterea lui K fata de 1 nu influenteaza practic rezultatul):
![]() (1.24)
(1.24)
1.3.3. Comparatia 1:n
La comparatia n masurandul este comparat cu o marime de referinta de valoare sensibil diferita (masurandul si referinta au valori in raportul n, unde n1). In laboratoarele de metrologie aceasta metoda este folosita frecvent pentru intercompararea etaloanelor de valori diferite sau pentru masurarea de valori situate intre cele ale unor etaloane de valoare unica.
Exista doua posibilitati de a compara simultan doi masuranzi de valori diferite: metode de aditionare (insumare), prin combinarea mai multor marimi astfel ca sa permita in final o comparatie 1:1, si metode de multiplicare (de raport), in care se foloseste un dispozitiv de raport, intermediar, pentru comparatie.
Metodele de aditionare sunt metode relativ complexe, care reclama marimi auxiliare, precum si un numar de comparatii 1:1, care sa conduca in final la comparatia n
Pentru a intelege ideea de baza a acestei metode, sa consideram urmatorul exemplu. Se cere sa se etaloneze o masa de 10 kg in raport cu o masa de 1 kg, a carei valoare este cunoscuta. Pentru aceasta se vor folosi masele auxiliare 1 kg, 1 kg, 2 kg si 5 kg, ale caror valori nu trebuie cunoscute cu precizie. Se procedeaza in felul urmator:
-se etaloneaza prima masa auxiliara de l kg prin comparatie cu etalonul de referinta de l kg;
-se etaloneaza in acelasi fel a doua masa auxiliara de 1 kg;
-se etaloneaza masa auxiliara de 2 kg in raport cu doua dintre masele de 1 kg, acum cunoscute cu precizie;
-se etaloneaza masa auxiliara de 5 kg prin comparatie cu masa insumata 1+1+1+2 kg;
-se etaloneaza masa de 10 kg prin comparatie cu masa insumata 1+1+1+2+5 kg, determinandu-se valoarea ei in raport cu masa de referinta cunoscuta.
Se observa ca in aceasta secventa de masurari au fost efectuate numai comparatii 1:1 care, pentru precizie maxima, pot fi facute prin substitutie sau prin permutare. In final insa masurarea este o comparatie 1:10.
Metodele de aditionare au numeroase variante, specifice unor domenii de masurare si unor masuranzi. Multe din acestea constau in efectuarea unui numar de m comparatii intre n masuranzi, obtinandu-se astfel m ecuatii, cu ajutorul carora se pot exprima valorile a n-1 masuranzi in functie de valoarea celui de-al n-lea masurand, considerat de valoare cunoscuta (luat ca referinta). Este necesar ca m sa fie cel putin egal cu n-1. Daca m=n-1, numarul ecuatiilor este egal cu numarul necunoscutelor. Daca insa m > n-1, sistemul de ecuatii este supradeterminat si in general este incompatibil; ecuatiile suplimentare pot fi insa folosite pentru evaluarea incertitudinii de masurare. In acest scop, se pot aplica diferite procedee matematice bazate pe metode ale teoriei probabilitatilor.
In general, o metoda de masurare in care se compara mai multi masuranzi, efectuandu-se un numar de comparatii mai mare decat cel minim necesar, se numeste metoda de masurare in serie inchisa. Daca numarul acestor masuranzi este n, primele n-1 comparatii conduc la un sistem de ecuatii independente; a n-a ecuatie poate fi folosita pentru verificarea 'inchiderii' seriei de masurari.
Metodele de aditionare se folosesc pentru compararea etaloanelor de masa, de lungime, de rezistenta electrica, de capacitate electrica etc.
Metodele de multiplicare utilizeaza un dispozitiv de raport care permite compararea simultana a doua marimi de valori diferite. Este necesar, de asemenea, un aparat de comparatie.
De cele mai multe ori, metodele de multiplicare sunt metode de zero, in care una dintre marimi este comparata cu un multiplu sau cu o fractiune a celeilalte marimi. Raportul de multiplicare sau de divizare este un numar adimensional stabilit cu ajutorul dispozitivului de raport.
Un exemplu de metoda de multiplicare este compararea a doua mase cu ajutorul unei balante cu brate neegale. Masa de masurat este data de o relatie de forma (1.17) in care insa l si l pot diferi mult. Precizia metodei depinde nemijlocit de precizia raportului l /l
In masurarile electrice, metodele de multiplicare - cunoscute aici mai mult sub denumirea de metode de raport - sunt folosite pe scara larga. Ele au deseori o precizie foarte ridicata deoarece precizia dispozitivelor de raport electrice poate sa fie foarte buna.
Ecuatia generala a metodelor de raport este
x = Kx (1.25)
unde K este raportul de multiplicare (divizare) al dispozitivului de raport.
Parametrul K poate avea una sau mai multe valori fixe; in acest caz, pentru obtinerea relatiei (1.25) este necesara varierea marimii de referinta x . Alte dispozitive de raport permit varierea raportului K in trepte fine astfel incat marimea de referinta x poate avea o valoare fixa (sau mai multe valori fixe).
1.4. Aparatul de masurat. Limitele preciziei instrumentale
Aparatul de masurat este mijlocul tehnic care serveste la obtinerea informatiei de masurare (a rezultatului masurarii). Caracteristicile metrologice ale unui aparat de masurat (in general ale unui mijloc de masurare) reprezinta ansamblul caracteristicilor acestuia care afecteaza rezultatul masurarii si in principal erorile cu care sunt furnizate informatiile de masurare.
Caracteristicile metrologice sunt urmatoarele: precizia instrumentala, sensibilitatea, pragul de sensibilitate, rezolutia, intervalul de masurare, puterea consumata, supraincarcabilitatea si fiabilitatea metrologica.
Una dintre cele mai importante caracteristici metrologice este precizia instrumentala, descrisa cantitativ prin eroarea instrumentala, cu componentele ei: eroarea de baza (in conditii de referinta) si erorile suplimentare (datorate modificarii marimilor de influenta). Tendinta fireasca a producatorilor de mijloace de masurare este de a creste continuu precizia instrumentala. Judecand dupa evolutia acesteia in ultimele decenii, am fi tentati sa credem ca aceasta crestere a preciziei poate continua la nesfarsit. Dar lucrurile nu stau tocmai asa. Insusi modul in care sunt definite marimile fizice cu care operam curent ridica o bariera in fata incercarii de a impinge dincolo de anumite limite precizia instrumentala.
In fizica macroscopica marimile sunt definite ca medii statistice ale unor efecte microscopice. Daca dam masurandului niste variatii atat de mici incat acestea devin comparabile cu discontinuitatile materiei, este evident ca nu mai putem vorbi de 'medii statistice' ale acestor variatii iar masurarea lor isi pierde sensul. De exemplu, sa consideram masurarea unui curent electric din ce in ce mai slab. Un curent foarte slab inseamna trecerea unui numar mic de electroni prin sectiunea conductorului. Un curent de 10- A este echivalent cu trecerea a aproximativ sase electroni pe secunda. Precizia cu care poate fi masurat un asemenea curent (care poate interveni in practica, de pilda in studiul unor fenomene de ionizare sau la masurari asupra materialelor electroizolante speciale) este scazuta deoarece el nu mai poate fi considerat un curent continuu propriu-zis ci un curent pulsator (fiecare electron produce un 'impuls' de curent), pentru a carui mediere ar fi necesar un timp indelungat. Masurarea unor curenti si mai slabi incepe sa-si piarda sensul: masurarea ar putea fi imaginata cel mult prin numararea electronilor unul cate unul!
O a doua categorie de limite naturale ale preciziei instrumentale provine din prezenta fenomenelor de fluctuatie in orice corp, fluctuatie care se manifesta in diferite moduri si care este denumita generic 'agitatie termica'. Denumirea este justificata de faptul ca agitatia termica scade in intensitate pe masura ce scade temperatura, ajungand sa se anuleze la temperatura de zero absolut. Macroscopic, agitatia termica isi face simtita prezenta prin fluctuatia unor marimi fizice masurabile cu aparate obisnuite dar de sensibilitate foarte mare. Astfel, un corp suspendat de un fir flexibil executa miscari neregulate chiar daca este izolat de orice interactiune cu vreo forta exterioara, din cauza 'bombardamentului' cu moleculele gazului inconjurator; fenomenul se poate observa la galvanometre extrem de sensibile, care nu pot fi 'linistite' complet, chiar ferite de orice perturbatie mecanica sau electrica exterioara. Un alt exemplu il constituie aparitia la bornele unui rezistor a unei tensiuni fluctuante, masurabile (numita tensiune de zgomot), chiar daca este eliminata orice sursa electrica posibila in circuitul in care se face masurarea.
Pe baza fizicii statistice, toate aceste fenomene pot fi explicate si se dovedeste ca ele au o origine comuna. Fenomenul de agitatie termica afecteaza orice masurare, fie ea mecanica, optica, electrica, termica sau de alta natura, daca marimea masurata are valoarea sub anumite limite. Cantitativ, zgomotul de agitatie termica al unui rezistor este dat de formula lui Nyquist
![]() (1.26
a)
(1.26
a)
sau
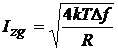 , (1.26
b)
, (1.26
b)
unde k=1,38.10- J/K este constanta lui Boltzmann, T -temperatura absoluta, f - banda de frecvente in care se face masurarea, Uzg -valoarea efectiva a tensiunii echivalente de zgomot iar Izg -valoarea efectiva a curentului echivalent de zgomot.
Exemplu. Pentru un rezistor cu rezistenta de 10 k, aflat la temperatura T=300 K, valoarea efectiva a tensiunii de zgomot in banda de frevente 0 ‑ 10 kHz este de aproximativ 1 V iar in banda de frevente 0 ‑ 1 MHz este de 10 V.
Formulele (1.26 a) si (1.26 b) conduc la relatia:
Pzg = kTf, (1.27)
in care Pzg=(Uzg) 4R este puterea de zgomot intr-o rezistenta egala cu R.
Intre banda de frecvente a mijlocului de masurare si timpul de crestere tr al marimii de iesire exista relatia
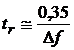 (1.28)
(1.28)
Pe de alta parte, se poate considera ca la un aparat cu regimul dinamic optimizat, indicatia aparatului ajunge la valoarea finala dupa aproximativ 3tr, deci
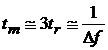 (1.29)
(1.29)
poate fi admisa ca durata unei masurari. Inlocuind in relatia (1.27), se obtine
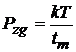 (1.30)
(1.30)
In aparatele de masurat reale, pe langa zgomotul propriu Pzg, exista un zgomot suplimentar, numit zgomot instrumental, datorat altor fenomene, perturbatiilor exterioare si diferitelor surse de fluctuatii. Se defineste factorul de zgomot F ca raport intre puterea totala de zgomot si puterea de zgomot propriu
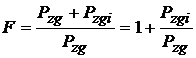 ,
,
unde Pzgi este puterea de zgomot instrumental (definitia este data pentru o anumita rezistenta a sursei de zgomot Pzg, considerata ca rezistenta optima pentru aparatul de masurat).
Factorul de zgomot este o caracteristica importanta a aparatelor de masurat la care se cauta realizarea unui prag de sensibilitate optim. El arata de cate ori este mai mare zgomotul unui aparat real fata de zgomotul unui aparat ideal, la care Pzgi=0. La aparatele de masurat uzuale factorul de zgomot poate avea valori mari, de ordinul zecilor, sutelor sau chiar mai mult. In schimb, la aparatele special construite pentru a masura tensiuni sau curenti foarte mici, factorul de zgomot se apropie de valoarea limita 1. In tabelul 1.1 sunt date, pentru exemplificare cateva valori tipice ale factorului de zgomot exprimate in decibeli, ca 20 lgF.
Se poate deduce concluzia ca la aparatele de masurat care au o rezolutie suficienta, pragul de sensibilitate este limitat de puterea de zgomot totala (egala cu suma puterilor de zgomot termic si instrumental). Daca se admite ca puterea cedata aparatului de masurare Pm trebuie sa fie cel putin egala cu puterea totala de zgomot FPzg pentru a putea sesiza o variatie a indicatiei aparatului,
Pm FPzg, (1.32)
se ajunge la relatia fundamentala
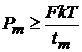 , (1.33)
, (1.33)
care precizeaza puterea minima de masurare necesara pentru a se atinge limita pragului de sensibilitate al aparatului de masurat.
Tabelul 1.1. Valori tipice ale factorului de zgomot la cateva tipuri de aparate de masurat
|
A p a r a t u l |
Factorul de zgomot [dB] |
|
Galvanometru magnetoelectric | |
|
Galvanometru vibrator | |
|
Amplificator de c.a. selectiv | |
|
Amplificator fotoelectric | |
|
Amplificator de c.c. cu modulator electromecanic | |
|
Amplificator de c.a. cu detectie sincrona | |
|
Amplificator de c.a. cu condensator vibrant |
Pragul de sensibilitate in putere al unui aparat are deci o limita naturala (deoarece F>1), care depinde numai de temperatura la care se face masurarea si de durata masurarii. Practic, temperatura este impusa - cu exceptia unor aparate de masurat speciale care lucreaza la temperaturi foarte joase. Singura posibilitate de a micsora pragul de sensibilitate ramane cresterea duratei masurarii, prin medierea rezultatelor partiale sau prin marirea constantei de timp a aparatului (in unele cazuri speciale, din aceasta cauza se folosesc durate de masurare tm de zeci sau chiar sute de secunde).
Pentru aparatele care masoara tensiune, respectiv curent, se pot scrie relatiile:
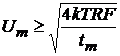 , (1.34 a)
, (1.34 a)
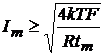 , (1.34 b)
, (1.34 b)
unde Um este tensiunea masurata iar Im - curentul masurat. Relatiile (1.34) arata ca pragurile de sensibilitate in tensiune si in curent depind, in afara de T, F si tm si de rezistenta interna R a sursei. Praguri de sensibilitate mici in tensiune se pot obtine in cazul surselor cu rezistenta interna mica, iar praguri de sensibilitate mici in curent se pot obtine in cazul surselor cu rezistenta interna mare.
1.5. Probleme
1.5.1. Cu ajutorul unei punti Wheatstone echilibrate se compara intre ele mai multe rezistoare avand rezistenta cuprinsa intre 10 000 si 10 010 . Erorile rezistentelor ce compun rezistorul variabil al puntii nu depasesc 0,02 %. Neglijand celelalte surse de erori, sa se determine incertitudinea comparatiei. Sa se estimeze, pe de alta parte, incertitudinea aferenta masurarii unei singure rezistente, admitand pentru toate rezistoarele puntii incertitudini de +0,02 %.
Solutia 1. Compararea intre ele a mai multor rezistoare utilizand puntea Wheatstone poate fi asimilata metodei de masurare diferentiale, descrisa de relatia (1.1) in care x este rezistenta masurata, x - valoarea de referinta (10 000 ) iar d - diferenta masurata direct, avand valori cuprinse intre 0 si 10 . Aceasta asimilare este posibila deoarece in rezistorul variabil al puntii, rezistenta de 10 000 ramane nemodificata; se modifica numai rezistenta ultimelor ranguri (ohmi si zecimi de ohm).
Aplicarea relatiei (1.4) ne arata ca eroarea relativa de masurare a oricarei rezistente din gama precizata - se compune dintr-un termen constant x /x si dintr-un termen care depinde de valoarea lui d, (d/x)*(d/d), in care
d/d = 0,02 % = 2*10-
Ca urmare, incertitudinea comparatiei intre doua rezistoare este data de acest termen, a carui valoare maxima se obtine pentru
d si este:
+(10 = +0,2 ppm.
Prin urmare, pentru orice pereche de rezistoare din gama specificata in enunt, incertitudinea comparatiei este de cel mult +0,2 ppm.
In cazul masurarii unei singure rezistente, incertitudinea aferenta (calculata ca eroare limita, prin aplicarea regulilor cunoscute de la propagarea erorilor) se obtine prin insumarea incertitudinilor rezistoarelor din celelalte trei brate ale puntii, adica
= + (0,02 + 0,02 + 0,02) % = + 0,06 % = + 6*10-
Observatie Compararea intre ele a mai multor rezistoare avand rezistente de valori apropiate se poate face mult mai precis decat masurarea unei valori individuale (in exemplul considerat, diferenta este de trei ordine de marime !).
Solutia 2 Toate rezistoarele sunt comparate cu un rezistor de referinta, Rref aflat intr-unul din bratele puntii. Se poate scrie:
Ri Rref i + i, (1.35)
unde i este modificarea relativa a rezistentei variabile a puntii, necesara pentru a aduce puntea la echilibru, iar + este incertitudinea relativa aferenta acestei modificari a rezistentei variabile (conform enuntului, avem
Pentru un alt rezistor Rj, avem
Rj Rref j + j. (1.36)
Exprimam pe j sub forma j = i + , unde este diferenta dintre j si i.
Raportul Ri Rj rezulta
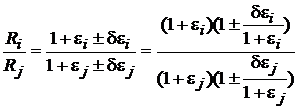 .
.
Tinand cont ca i si j sunt mici fata de 1, se poate scrie:
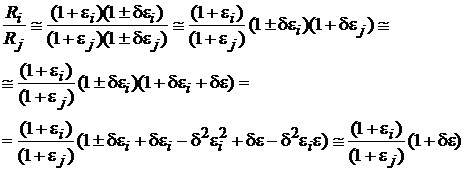
In aceasta expresie, (1+i) j) reprezinta valoarea raportului celor doua rezistente, iar reprezinta incertitudinea comparatiei. Valoarea maxima a acestei incertitudini se obtine pentru valoarea maxima a lui , care, cu valorile din enunt este
Prin urmare, incertitudinea comparatiei este de cel mult
= +0,2 ppm.
1.5.2. Aceeasi problema pentru rezistoare cu rezistenta cuprinsa intre 9 995 si 10 005 . Se vor avea in vedere doua cazuri privind modul de obtinere a valorilor mai mari de 10 000 ale rezistorului variabil Rv:
a).9*1 000 +n*1
b).1*10 000 +n*1
Solutie. Rezistentele pot fi impartite in doua grupe valorice: 9 995‑10 000 si 10 000-10 005 . Indiferent de modul de obtinere a valorii lui Rv, oricare doua rezistente din aceeasi grupa valorica se compara cu o incertitudine de cel mult +0,1 ppm, obtinuta ca in problema 1.5.1.
Compararea a doua rezistente din grupe valorice diferite se face cu incertitudini diferite, in functie de modul de obtinere a valorii lui Rv.
Astfel, in cazul a, in valorile lui Rv mai mari decat 10 000 apare in plus o rezistenta de 10 , cunoscuta cu o incertitudine de +2*10 , adica de . Relativ la valoarea de 10 000 , aceasta incertitudine este de +2*10- . Ea trebuie adaugata la valoarea de +0,1 ppm determinata mai sus si, prin urmare, incertitudinea comparatiei este de cel mult +0,3 ppm.
Daca valorile mai mari decat 10000 ale lui Rv se obtin ca in cazul b, atunci compararea a doua rezistente din grupe valorice diferite poate fi asimilata compararii a doua rezistente de 10 000 una cu eroare maxima pozitiva (+0,02%) si una cu eroare maxima negativa (-0,02%), caz in care incertitudinea comparatiei devine +0,04%. In practica, aceasta situatie poate sa apara daca erorile tuturor rezistentelor de 1000, 100, 10 si 1 sunt maxime pozitive iar eroarea primei rezistente de 10 000 este maxima negativa (sau invers). Situatia descrisa este putin probabila, dar totusi posibila. Din acest motiv, compararea rezistentelor din cele doua grupe valorice trebuie facuta ca in cazul a, in care incertitudinea comparatiei este mult mai mica.
1.5.3. O tensiune continua Ux, de aproximativ 1,018 V, se masoara prin metoda diferentiala directa. Se folosesc in acest scop un element normal (Weston) avand t.e.m. EN=1,018535 V, cunoscuta cu o incertitudine de +1V, si un microvoltmetru cu domeniul de 100 V si clasa de precizie 1.
Sa se determine Ux si incertitudinea masurarii, stiind ca microvoltmetrul a indicat 78V.
Solutie. Aplicand relatiile (1.1) si (1.4), obtinem:
Ux=1,018535 V+78*10- V=1,018613 V
si
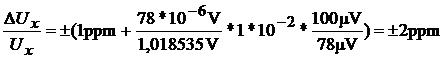 .
.
In concluzie,
Ux=1,018613 V+2 V.
Se observa ca desi incertitudinea care afecteaza diferenta tensiunilor este mare (1,3%), ea conduce la o incertitudine mica a lui Ux (1ppm) deoarece diferenta masurata direct este mica (78V) fata de Ux (1V).
1.5.4. O punte Wheatstone cu brate egale (fig. 1.5) are raportul K putin diferit de 1 datorita faptului ca rezistentele R si R sunt afectate de erorile de +0,1% si respectiv -0,2%. Sa se calculeze valoarea reala a lui K si sa se determine valoarea lui Rx daca echilibrul puntii s-a obtinut pentru
R
|
Solutie. Relatia de calcul pentru Rx este Prin urmare, avem Rezulta Rx=1,003*1012,3 |
Fig. 1.5. Pentru problema 1.5.4. |
1.5.5. Un condensator etalon Cx avand valoarea nominala a capacitatii de 100 000 pF se masoara prin metoda substitutiei, folosind o punte de curent alternativ cu raportul K1, un condensator etalon C =100 000 pF cu incertitudinea de +1 pF si un condensator tara de aproximativ 100 000 pF. Pentru condensatorul variabil al puntii s-au obtinut valorile 100 011 pF la masurarea condensatorului necunoscut si 100 024 pF la masurarea condensatorului etalon C
Sa se determine capacitatea Cx si sa se estimeze incertitudinea de masurare.
Solutie. Se aplica relatia (1.16) in care se iau k =0,000011 si k =0,000024, obtinandu-se
Cx=100 000(1+0,000011-0,000024)=99 987 pF.
Incertitudinea de masurare, in ipoteza ca se neglijeaza eroarea datorata pragului de sensibilitate al puntii, este egala cu incertitudinea etalonului, adica +1 pF.
1.5.6. Pentru masurarea capacitatii condensatorului din problema 1.5.5, din cauza lipsei unui condensator tara, se foloseste metoda Gauss (metoda permutarii), la cea de-a doua masurare locurile condensatoarelor Cx si C fiind inversate fata de situatia prezentata in fig. 1.6. La prima masurare se obtine Cx=1,00087 C , iar la cea de-a doua C =1,00113 Cx.
Sa se determine valoarea lui Cx si sa se estimeze incertitudinea de aferenta.
|
Solutie. Aplicand relatia (1.22), se obtine de unde Cx=0,99987 C =99 987 pF. Incertitudinea de masurare, in conditiile problemei 1.5.5, poate fi estimata la +1 pF. |
Fig.1.6. Pentru problema 1.5.6. |
1.5.7. Daca raportul K al unui dispozitiv de raport se exprima aproximativ printr-un numar intreg, el poate fi determinat prin metoda permutarii generalizate. De exemplu, in cazul unei balante cu raportul bratelor K10, se folosesc 11 greutati avand masele x , x ,, x aproximativ egale, dar necunoscute. Se fac 11 masurari, astfel: se compara masa x cu masa insumata x +x ++x pusa pe celalalt platan; se noteaza cu a indicatia balantei, corespunzatoare masei care trebuie adaugata la x pentru echilibrarea balantei; se schimba apoi x cu x si se compara x cu masa insumata x +x ++x s.a.m.d. Se obtin astfel 11 indicatii ale balantei.
Sa se scrie ecuatiile care rezulta si sa se deduca expresia raportului K in functie de cele 11 rezultate.
Solutie. Fie K=10(1+k), unde k este un factor de corectie al raportului balantei.
Ecuatiile pentru fiecare masurare sunt urmatoarele:
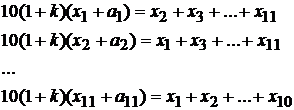 (1.38)
(1.38)
Prin insumarea celor 11 ecuatii rezulta
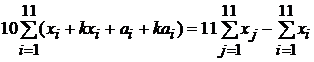 , (1.39)
, (1.39)
de unde, prin transformari elementare si neglijarea termenilor kai, se obtine:
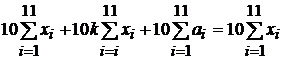 (1.40)
(1.40)
si, in final
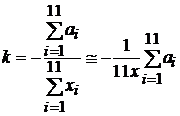 , (1.41)
, (1.41)
in care x este masa aproximativa a fiecareia dintre cele 11 greutati.
Exemplu numeric. Fie 1 kg masa nominala a celor 11 greutati si 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 si 11 g masele corespunzatoare celor 11 indicatii ale balantei. Cu relatia (1.41) se obtine:
![]()
deci K=10(1-6*10
1.5.7. Raportul de divizare al divizorului autocalibrabil din fig. 1.7 are valoarea nominala Kn=10. Valoarea reala a acestui raport este afectata de un factor de corectie k, K=Kn(1+k), care trebuie determinat. In acest scop, se compara rezistentele R , R , R si R cu R , obtinandu-se urmatoarele rezultate:
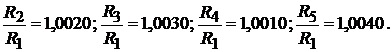
Se compara apoi R cu suma R +R +R +R +R , obtinandu-se:
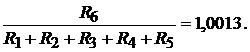
Sa se calculeze factorul de corectie k si sa se estimeze incertitudinea reziduala care afecteaza raportul de divizare, determinata de incertitudinea comparatiei (erorile rezistentelor ce compun rezistorul variabil al puntii de comparatie nu depasesc +0,02%). Cu cate cifre semnificative se va specifica factorul de corectie?
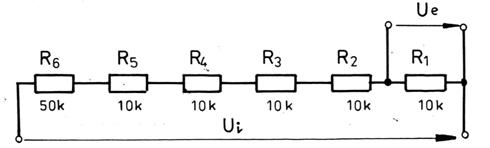
Fig. 1.7. Pentru problema 1.5.7.
Solutie. Raportul de divizare este dat de relatia
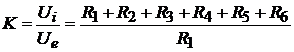 , (1.42)
, (1.42)
din care obtinem succesiv
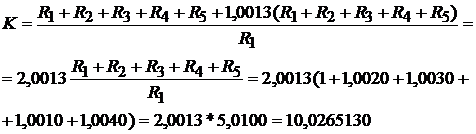
Rezulta factorul de corectie
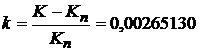 .
.
In realitate, rapoartele Ri R se cunosc cu incertitudinile i datorate comparatiei:
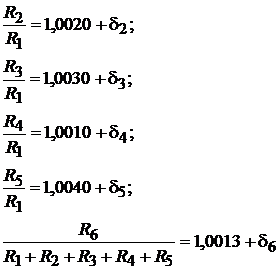
Ca urmare, raportul de divizare devine:
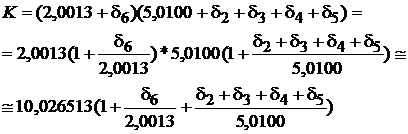
Termenul
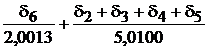
reprezinta incertitudinea reziduala, pe care o notam cu r. Pentru calculul sau trebuie determinate valorile i. Acestea rezulta prin inmultirea incertitudinii de 0,02% (a rezistentelor ce compun rezistorul variabil al puntii de comparatie) cu abaterea fata de 1 a raportului Ri R . Astfel, pentru avem:
Pentru celelalte incertitudini se obtin valorile: , , si . Ca urmare, incertitudinea reziduala va fi
r=+0,53 ppm.
Tinand cont de faptul ca incertitudinea de masurare trebuie exprimata cu una sau cel mult doua cifre semnificative (adica +0,6 ppm sau +0,53 ppm), factorul de corectie poate fi precizat in doua moduri:
k=0,0026513+0,0000006
sau
k=0,00265130+0,00000053,
ambele variante fiind corecte.
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |