
Relatii booleene cu diagrame Venn
In ultimul exemplu din sectiunea precedenta, multimile A si B s-au suprapus partial. Initial, ne vom concentra atentia asupra intregii regiuni hasurate de mai jos, abia apoi vom trece la analizarea regiunii comune celor doua multimi. Sa utilizam expresii booleene pentru desemnarea regiunilor diagramelor Venn, conform figurii de mai jos:
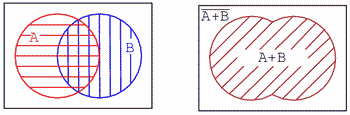
Aria multimii A este hasurata cu rosu, iar cea a multimii B cu albastru. Daca analizam intreaga aria hasurata (suma totala a tuturor ariilor hasurate), indiferent de culoare sau stil, obtinem figura din dreapta sus. Aceasta corespunde functiei logice SAU, iar expresia booleana este A + B, aria fiind cea hasurata cu linii diagonale. Tot ceea ce se afla in afara ariei hasurate reprezinta (A + B)'.
O alta metoda de interpretare a diagramei Venn cu regiuni suprapuse, este analizarea regiunii comune atat multimii A cat si multimii B, aria dublu hasurata de mai jos (stanga). Aceasta arie corespunde functiei logice SI, iar expresia booleana este AB (jos dreapta). Tot ceea ce se afla in afara ariei dublu hasurate AB reprezinta (AB)':
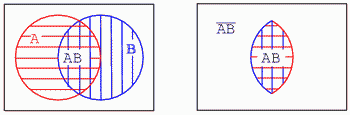
Observati ca unele elemente ale multimilor A si B de sus, sunt elemente ale multimii (AB)', dar niciunul dintre elementele multimii (AB)' nu se afla in interiorul ariei dublu hasurate AB.
Vom trece acum la dezvoltarea unor expresii booleene. De exemplu, sa presupunem ca dorim reprezentarea prin diagrame Venn a expresiei booleene A'B (A' SI B).
Pasii sunt urmatorii: hasurarea ariei A'; hasurarea ariei B; realizarea functiei SI (A'B) prin suprapunerea celor doua regiuni precedente. Am putea sa ne oprim aici, dar, pentru claritate, putem pastra doar aria dublu hasurata:
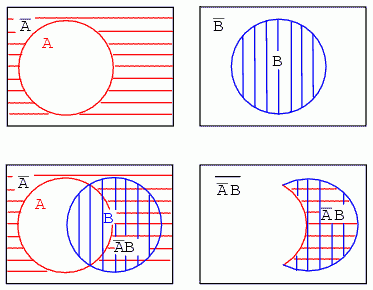
Expresia A'B reprezinta regiunea in care A' si B se suprapun. Regiunea nehasurata din afara ariei A'B este (A'B)'.
Putem incerca acelasi lucru cu expresia booleana SAU. De exemplu, sa presupunem ca dorim sa reprezentam prin diagrame Venn expresia B' + A.
Pasii sunt urmatorii: incepem cu hasurarea lui B, si apoi a regiunii B'; suprapunem A peste B'. Din moment ce suntem interesati de realizarea functiei SAU, vom cauta sa reprezentam intreaga arie formata de cele doua multimi, indiferent de stilul hasurarii. Prin urmare A + B' reprezinta intreaga arie hasurata:

Pentru claritate, putem reprezenta intreaga regiune printr-o singura hasura (jos stanga):

Aria hasurata cu verde de mai sus este rezultatul expresiei A + B'. Trecand la (A + B')', cautam complementul expresiei A + B', reprezentat prin aria nehasurata din figura de mai sus stanga. Aplicand teorema lui DeMorgan si negarea dubla (A'' = A), ajungem la rezultatul (A + B')' = AB'. Prin urmare, cele doua regiuni sunt identice.
Putem face acum observatia ca diagramele Venn nu demonstreaza nimic. Avem nevoie de algebra booleana pentru acest lucru. Totusi, diagramele Venn pot fi utilizate pentru verificare si vizualizare. In exemplul de mai sus, am verificat si vizualizat teorema lui DeMorgan cu ajutorului unei diagrame Venn.
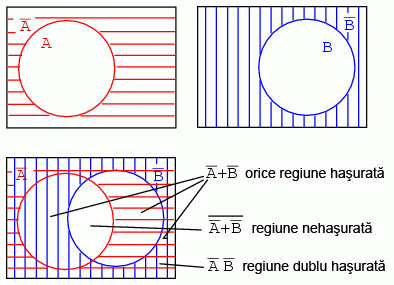
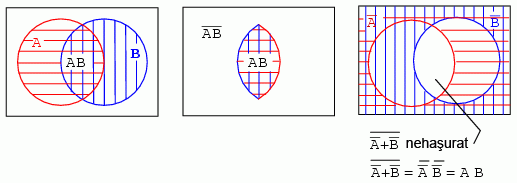
Diagrama Venn de mai jos contine trei regiuni hasurate, A (rosu), B (albastru) si C (verde). Intersectia tuturor regiunilor in centru reprezinta expresia booleana ABC. Exista o alta regiune unde A si B se intersecteaza, reprezentand expresia booleana AB. Similar, intersectia ariei A cu C si B cu C reprezinta expresia booleana AC, respectiv BC.
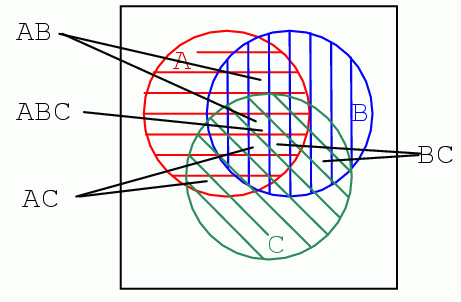
Observand marimea regiunilor descrise de functia SI de mai sus, putem vedea ca marimea regiunii variaza cu numarul variabilelor asociate expresiei SI.
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |