
ANALIZA SI SINTEZA MECANISMELOR CU ROTI DINTATE
1. Mecanisme cu roti dintate cu axe fixe - generalitati.
Prin definitie, raportul de transmitere dintre doua elemente A si B, aflate in miscare de rotatie instantanee sau permanenta, este raportul vitezelor lor unghiulare.
![]()
Daca n [rot/min] atunci ![]() [rad/sec].
[rad/sec].
Acest raport de transmitere se poate utiliza si la mecanismele cu parghii, dar numai la elemente care efectueaza rotatii.
1.1. Mecanisme plane cu roti dintate (angrenaje).
Un mecanism format din doua roti dintate conjugate in contact, avand axe fixe de rotatie, se numeste angrenaj.
Flancul unui dinte al rotii dintate reprezinta suprafata care margineste plinul dintelui (fata de golul dintre dinti), si care intra in contact cu flancul rotii dintate conjugate. Flancurile omoloage sunt acelea, care printr-o rotatie in jurul axei rotii dintate, se pot suprapune virtual.
Pasul este distanta, masurata in mm, pe un cerc oarecare al rotii dintate, dintre doua flancuri omoloage si succesive.
Din definitia pasului se deduce ca acesta are dimensiune de lungime si ca pe fiecare cerc, pasul are o alta valoare.
Din exprimarea lungimii unui cerc al rotii dintate in functie de diametru si de numarul de dinti, se poate deduce expresia modulului, care are si el tot dimensiune de lungime.

![]()
![]()
Fig. 72.
In continuare se iau in considerare, pentru problema rapoartelor de transmitere, rotile dintate evolventice nedeplasate.
Punctul de tangenta al centroidelor rotilor dintate, care sunt cercuri , se numeste polul angrenarii: P s C, si se gaseste pe linia centrelor O1O2.
Angrenajul denumit exterior este acela la care centrele rotilor dintate se afla de o parte si de cealalta a polului angrenarii (P s C este cuprins intre O1 si O2 - fig. 73 si fig. 103).
Angrenajul interior este acela la care centrele rotilor dintate se afla de aceeasi parte a polului angrenarii (P s C se afla in exteriorul lui O1O2).
Rotile luate in studiu au dinti evolventici.
Evolventa este curba descrisa de un punct solidar cu o dreapta (centroida sau rostogolitoarea mobila a evolventei) ce se rostogoleste (deci fara alunecare) peste un cerc denumit cerc de baza (centroida sau rostogolitoarea fixa a evolventei). Reciproc, cercul de baza reprezinta infasuratoarea normalelor la flancul evolventic al dintelui.
Tangenta interioara comuna la cercurile de baza, intersecteaza linia centrelor O1O2 in polul angrenarii P s C (a se vedea si fig. 103).
La angrenajul
exterior, vectorii viteze unghiulare ![]() si
si ![]() sunt de sens opus, si
de aceea i care este
raportul modulelor acestor vectori, se considera avand valoare negativa.
sunt de sens opus, si
de aceea i care este
raportul modulelor acestor vectori, se considera avand valoare negativa.
La angrenajul interior, i se considera avand valoare pozitiva.
Intr-o demonstratie grafica, dreapta de distributie a vitezelor liniare, este locul geometric al varfurilor vectorilor viteze liniare, apartinand punctelor de pe linia centrelor (deci originile vectorilor sunt situate pe linia centrelor), ale unei aceeasi roti dintate.
Viteza liniara a axei fixe de rotatie a rotii dintate este nula, vectorul degenerand si avand originea confundata cu varful.
Dreapta de distributie de viteze a unei roti dintate, se poate construi cand se cunosc vitezele liniare a doua puncte distincte ale rotii dintate, de pe linia centrelor.
Fie rotile i si j, conjugate.
Cu ![]() se noteaza viteza
liniara a polului angrenarii rotilor dintate i si j
se noteaza viteza
liniara a polului angrenarii rotilor dintate i si j
Cu (i ) si ( j ) se noteaza respectiv, dreptele de distributie de viteze liniare a celor doua roti dintate.
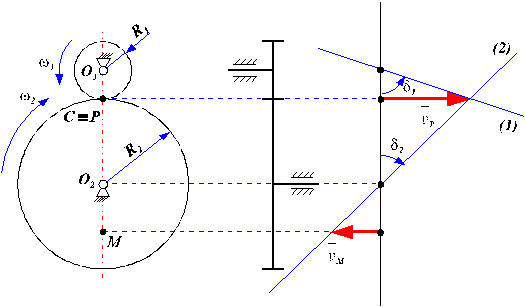
Fig. 73. Angrenaj exterior.
Cazul angrenajului exterior (fig. 73):
![]()
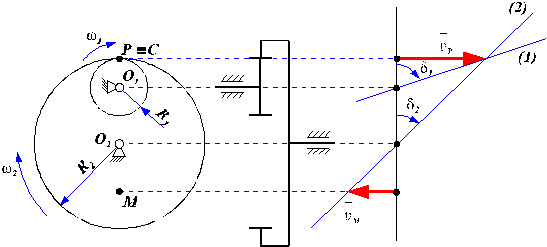
Fig.7 Angrenaj interior.
Cazul angrenajului interior (fig. 74):
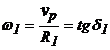
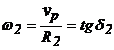
![]()
1.2. Tren de roti dintate cu axe fixe.
Este constituit dintr-o succesiune (serie sau paralel) de angrenaje. El are mobilitatea M=1. Exista deci un singur element conducator, corespunzand intrarii", restul elementelor fiind conduse. Miscarea se poate culege pe la unul sau mai multe elemente conduse, corespunzand "iesirii".
La un tren de roti dintate, rotile denumite "parazite", sunt acele roti ale caror numere de dinti nu apar in formula raportului de transmitere (z4 si z9 la trenul de roti dintate din figura 75).
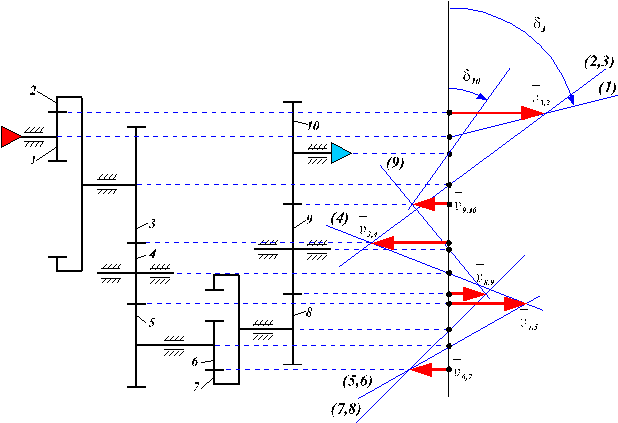
Fig. 75. Tren de roti dintate cu axe fixe.
Se cunosc: z1 z2 z10
Se cere: ![]()
Se observa ca: ![]() ;
; ![]() ;
; ![]() ;
;
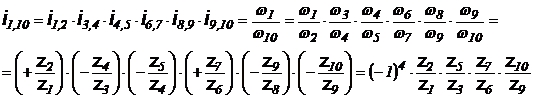
1.3. Realizarea cu roti dintate parazite a distantei mari intre axe.
Cand este necesara transmiterea miscarii (i impus) intre doua axe paralele, aflate la distanta mare, este nejudicios sa se foloseasca un singur angrenaj. Acesta trebuie inlocuit cu un tren de roti dintate cu axe fixe cuprinzand si roti dintate parazite, calculat astfel incat i , (al trenului de roti dintate) sa fie egal cu i . Acesta ocupa o suprafata frontala mult mai mica.
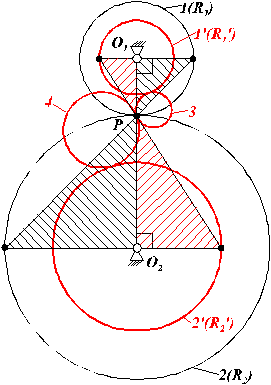
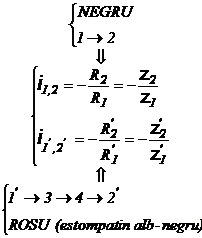
Din asemanarea triunghiurilor T
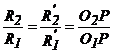
In concluzie ![]()
Fig. 76.
1. Inversoare de sens cu roti dintate parazite.
Un mecanism simplu si eficient, care poate realiza inversarea sensului de rotatie al elementului 2 de iesire, cand elementul 1 de intrare isi mentine sensul de rotatie, utilizeaza doua (3 si 4) respectiv o roata (4) parazita active.
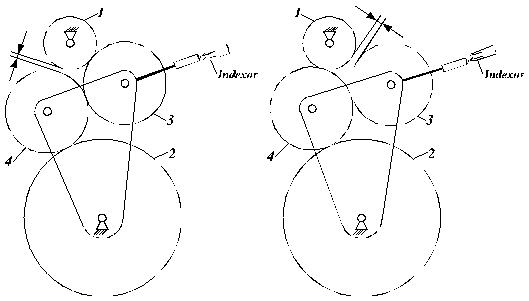
a. b.
Fig. 77. Inversoare de sens cu roti dintate parazite.
La acest tip de mecanism, prevazut si cu un indexor cu doua pozitii, inversarea de sens se poate efectua numai cu mecanismul oprit.
Cazul a. (fig. 77,
a): ![]()
![]()
Cazul b. (fig. 77,
b): 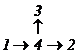
![]()
In timpul manevrarii manetei, cand mecanismul este oprit, rotile 3 si 4 au axele mobile rotindu-se in jurul axei rotii 2, purtate de placa triunghiulara, lagaruita tot pe axa rotii dintate 2. In timpul functionarii, rotile 3 si 4 au axele fixe, fiind lagaruite in placa triunghiulara.
2. Mecanisme cu roti dintate cu axa mobila - generalitati.
 Se mai
numesc mecanisme diferentiale si/sau planetare. Denumirea de diferentiale
provine de la faptul ca se poate realiza, cu ajutorul lor, o combinatie liniara
a doua viteze unghiulare date. Denumirea de planetare, provine de la miscarea
de revolutie combinata cu cea de rotatie proprie (similara miscarii planetei
Pamant in jurul stelei Soare) pe care o efectueaza rotile dintate denumite
satelit (denumire imprumutata tot din astronomie). In prezent aceste mecanisme
au o larga utilizare in reductoare si cutii de viteze compacte, automate, in
mecanisme de directie ale autovehiculelor grele pe senile, etc, ele constituind
in prezent o tehnica de varf, inclusiv la roboti.
Se mai
numesc mecanisme diferentiale si/sau planetare. Denumirea de diferentiale
provine de la faptul ca se poate realiza, cu ajutorul lor, o combinatie liniara
a doua viteze unghiulare date. Denumirea de planetare, provine de la miscarea
de revolutie combinata cu cea de rotatie proprie (similara miscarii planetei
Pamant in jurul stelei Soare) pe care o efectueaza rotile dintate denumite
satelit (denumire imprumutata tot din astronomie). In prezent aceste mecanisme
au o larga utilizare in reductoare si cutii de viteze compacte, automate, in
mecanisme de directie ale autovehiculelor grele pe senile, etc, ele constituind
in prezent o tehnica de varf, inclusiv la roboti.
a. b. c.
Fig. 78. Mecanisme cu roti dintate cu axa mobila.
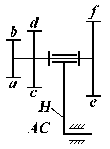
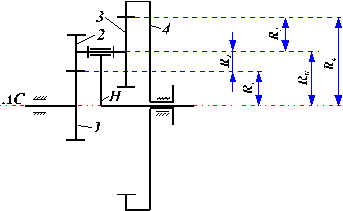
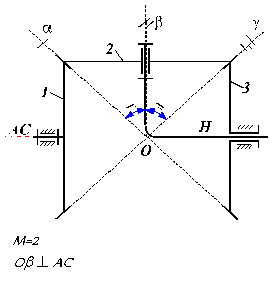
Elementul H este bratul port-satelit, care se roteste in jurul axei fixe, denumita axa centrala AC, care este axa sa de simetrie.
Roata centrala 2 se roteste tot in jurul axei centrale AC, care este axa sa de simetrie. Roata 2 impreuna cu H sunt denumite elemente centrale.
Satelitul 1 se roteste in jurul axei proprii de simetrie , datorita unei lagaruiri in bratul port-satelit, si impruna cu H in jurul axei centrale AC.
Tipurile uzuale de sateliti sunt cei mono, dublu sau triplu danturati exterior (fig. 79).

a. b. c.
Fig. 79. Tipuri de roti satelit.
a - satelit mono danturat exterior; b - satelit dublu danturat exterior;
c - satelit triplu danturat exterior.
Rotile centrale sunt fie danturate exterior (RE), fie interior (RI).
Numarul minim de roti centrale este egal cu numarul de danturari ale satelitului.
Numarul maxim de roti centrale este egal cu de doua ori numarul de danturari al satelitului.
a. b.
Fig. 80. Tipuri de roti centrale Fig. 81.
a - roata centrala danturata exterior; In a, c, e RE
b - roata centrala danturata interior. In b, d, f RI
Unitatea planetara (UP) este un mecanism cu roti dintate, avand un singur brat port-satelit si gradul de mobilitate M daca toate rotile centrale sunt mobile sau M=1 daca o roata mobila este fixata (restul fiind obligatoriu mobile). Fixarea bratului port-satelit H cand toate rotile centrale sunt mobile ar conduce la degenerarea mecanismului intr-un tren de roti dintate cu axe fixe. Fixarea simultana a doua elemente ar duce la blocarea mecanismului.
Intrarile si iesirile intr-o unitate planetara se fac de obicei pe la elementele centrale. Pentru a culege sau imprima rotatia proprie a satelitului, este necesar un mecanism auxiliar.
Tipurile de unitati planetare se determina in functie de numarul de danturari ale satelitului si de numarul si tipul (RE sau RI) de roti centrale.
Schema bloc a unei unitati planetare este sub forma unui dreptunghi, pe care sunt figurate si numerotate doar elementele centrale.
 a. b. c. d.
a. b. c. d.
Fig. 82. Tipuri de unitati planetare (M=2).

Daca M vor rezulta doua intrari si restul fiind iesiri; de exemplu:
Prin fixarea unei roti centrale, unitatea planetara isi reduce mobilitatea M de la 2 la 1; de exemplu fig. 83.

Fig. 83.
2.1. Raportul de transmitere la o unitate planetara (relatia lui Willis).
Se va da un calcul grafic si unul analitic al rapoartelor de transmitere la o unitate planetara cu M
Daca unitatea planetara are M=1, in relatii se introduce valoarea zero pentru viteza unghiulara w a rotii dintate centrale fixe.
Pentru calculele analitice se aplica metoda inversiunii miscarii, care in acest caz revine la a imprima virtual, intregului mecanism, o rotatie in jurul axei centrale AC, egala si de sens opus cu rotatia bratului port-satelit. In miscarea inversata, axa proprie a satelitului devine virtual fixata, mecanismul transformandu-se intr-un tren de roti dintate cu axe fixe, si putandu-se aplica relatiile analitice proprii acestui tip de mecanism. Pentru a se distinge ca relatia raportului de transmitere a fost determinata intr-o miscare inversata, la exponentul lui i din acest caz, se va trece indicele H.
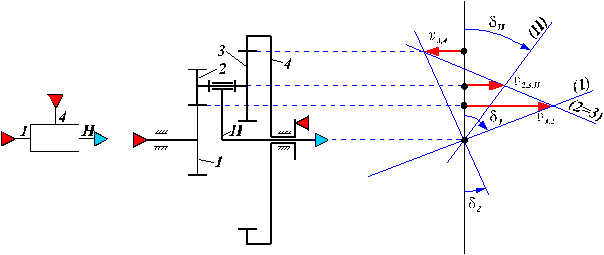
Fig. 8
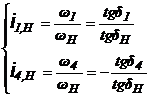
Date: ![]() si
si ![]() cu
cu ![]() .
.
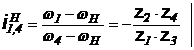 Relatia lui
WILLIS
Relatia lui
WILLIS
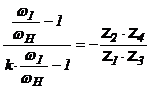
Deci 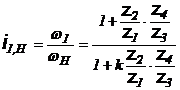 si
si 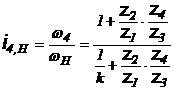 .
.

Variante:
TABELUL 1.
Elementul |
||||
|
s |
H |
|||
|
w in miscarea reala |
|
|
|
|
|
w in miscarea inversata |
|
|
|
|
Numarul de dinti al rotilor dintate dintr-o unitate planetara trebuie sa indeplineasca conditiile de coaxialitate, de montaj si de vecinatate. Pentru ultimele doua se va consulta bibliografia.
 Modulul
rotilor
Modulul
rotilor
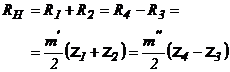
Daca ![]() atunci
atunci
![]()
Fig. 85.
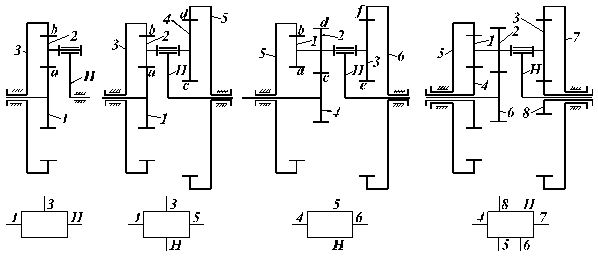
2.2. Mecanisme complexe continand unitati planetare.
Sunt formate din una sau mai multe unitati planetare legate in diferite moduri.
Lantul de inchidere este un tren de roti dintate cu axe fixe, care leaga prin exterior doua elemente centrale ale aceleiasi unitati planetare. Acest fapt echivaleaza cu impunerea unei relatii liniare intre vitezele unghiulare a doua elemente centrale, ceea ce face ca lantul de inchidere sa nu poata fi creat decat la unitati planetare cu M . Deci in urma crearii lantului de inchidere, mecanismul complex format din ansamblul unitate planetara plus lant de inchidere va avea mobilitatea M
Exemplele de variante de creere a lantului de inchidere la o unitate planetara cu patru elemente centrale
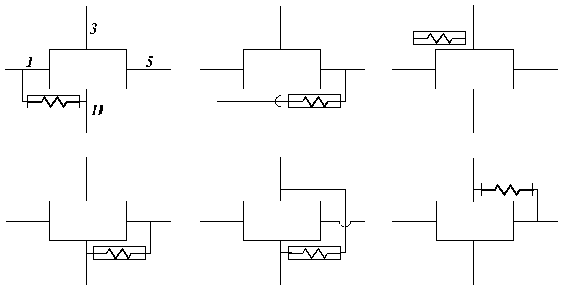
Fig. 86.
Cand mecanismul complex contine doua sau mai multe unitati planetare, se folosesc fie lanturi de legatura, care pot fi trenuri de roti dintate cu axe fixe fie solidarizari intre elementele centrale a unor unitati planetare diferite.
Calculul rapoartelor de transmitere la un mecanism complex continand unitati planetare, trebuie sa respecte urmatoarea metodologie
Se depisteaza toate unitatile planetare componente: pentru determinarea elementelor unei unitati planetare se cauta mai intai bratul port-satelit cu satelitii ce-i poarta; rotile centrale ale unitatii planetare sunt doar acelea care angreneaza cu danturile satelitului; alte roti dintate avand ca axa de simetrie si rotatie axa centrala dar care nu angreneaza cu vreuna din danturile satelitilor nu sunt roti centrale.
Se cauta lanturile de inchidere a unitatilor planetare si lanturile de legatura dintre unitatile planetare.
Se determina relatiile dintre wi si zi la fiecare unitate planetara.
Se determina relatiile dintre wi si zi la lanturile de inchidere si de legatura.
Se formeaza un sistem liniar cu relatiile determinate, din care prin rezolvare se determina raportul de transmitere dintre intrare si iesire.
2.3. Rezolvarea grafica si analitica a unui mecanism complex continand
unitati planetare.
S-a ales pentru studiu, un mecanism complex, continand o unitate planetara cu lant de inchidere plus o unitate planetara cu un element fixat, intre ele existand un lant de legatura.
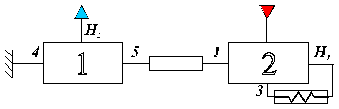
Se cunoaste: z1 z2 z3 z17
Se cere: 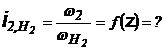
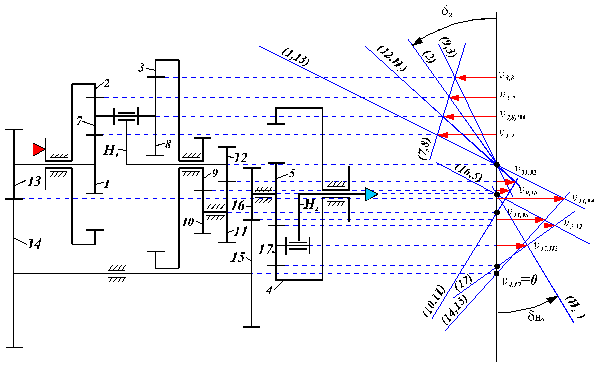
Fig. 87.
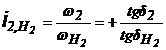
Algoritmul rezolvarii grafice:
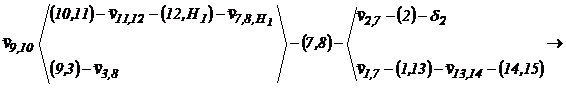
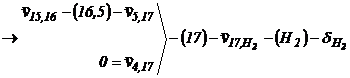
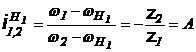
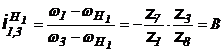
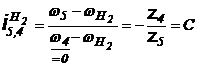
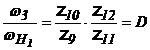 ;
; ![]()
![]() ;
; ![]()
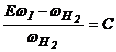 ;
; 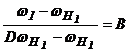 ;
;
![]()
![]() ;
; 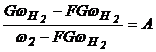
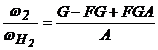
2. Unitati planetare cu roti conice - diferentialul auto.
La acestea, axa centrala AC si cu axa proprie de rotatie a satelitilor sunt concurente in punctul O.
Din acest motiv, la aplicarea virtuala
a unei inversiuni a miscarii pentru intregul mecanism, cu ![]() , se deduce ca axa instantanee de rotatie a satelitului este
generatoarea Oa, deoarece
roata 1 devine virtual fixa, deci
, se deduce ca axa instantanee de rotatie a satelitului este
generatoarea Oa, deoarece
roata 1 devine virtual fixa, deci ![]() . Elementul satelit 2
are atunci o miscare sferica de centru O.
. Elementul satelit 2
are atunci o miscare sferica de centru O.
 Ecuatia lui Euler:
Ecuatia lui Euler: ![]()
Se
cunoaste: ![]() si
si ![]()
Se
cere: ![]()
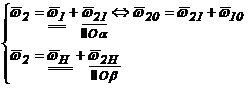
S-a facut notatia: 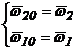
Fig. 88.
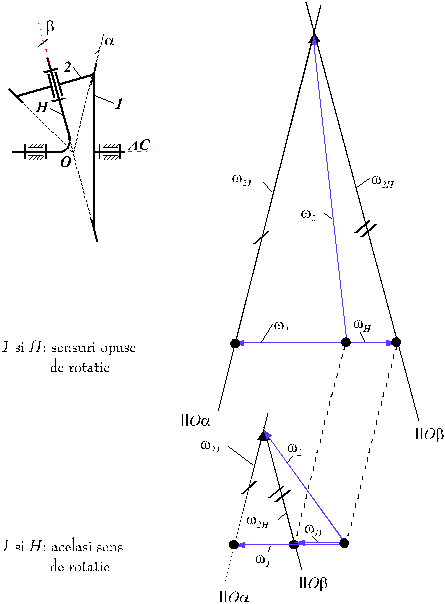
Fig. 89.
Faptul ca ![]() se poate observa usor
pe orice autovehicul dotat cu diferential (fig. 90 si fig. 92): se suspenda puntea motoare, se
blochiaza arborele cardanic sau pinionul de atac introducand maneta de viteze intr-una din viteze,
motorul fiind oprit. Se roteste una dintre roti si se observa o rotatie egala dar
de sens opus la cealalta roata. In aceasta situatie, diferentialul se
transforma intr-un tren de roti dintate conice cu axe fixe, la care roata
satelit 2 s-a transformat in roata
dintata parazita.
se poate observa usor
pe orice autovehicul dotat cu diferential (fig. 90 si fig. 92): se suspenda puntea motoare, se
blochiaza arborele cardanic sau pinionul de atac introducand maneta de viteze intr-una din viteze,
motorul fiind oprit. Se roteste una dintre roti si se observa o rotatie egala dar
de sens opus la cealalta roata. In aceasta situatie, diferentialul se
transforma intr-un tren de roti dintate conice cu axe fixe, la care roata
satelit 2 s-a transformat in roata
dintata parazita.
Se
cunoaste: ![]() si
si ![]()
Se
cere: ![]()
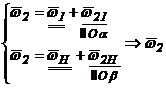
![]()
Fig. 90.
Cazul: ![]() .
.
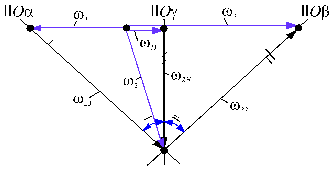
Fig. 91.
Cazul: ![]()
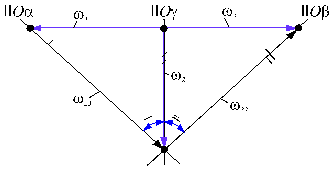
Din asemanarea triunghiurilor rezulta:
![]()
Fig. 92.
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |