
Relatii intre deplasari si deformatii
Se considera mai intai o stare liniara de tensiuni reprezentata printr-o bara dreapta solicitata la intindere, (fig.12), raportata la axa Ox cu originea in sectiunea marginala din stanga. Prin deformarea barei, sectiunea sa transversala l se va deplasa axial cu cantitatea u. Sectiunea 2 aflata la distanta dx de l, va suferi o deplasare u + du. Lungirea specifica pe directia axei barei va fi,
![]()
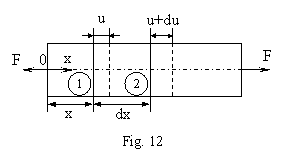
 In
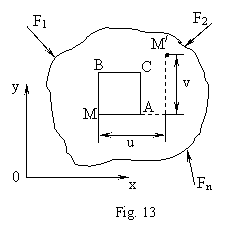
continuare se considera o placa aflata intr-o stare plana
de tensiuni (fig.13). Un punct oarecare M se va deplasa prin deformarea
placii atat in directia axei Ox cat si in directia axei Oy.
Cele doua deplasari se noteaza prin u = u(x, y) si v = v(x,
y).
In
continuare se considera o placa aflata intr-o stare plana
de tensiuni (fig.13). Un punct oarecare M se va deplasa prin deformarea
placii atat in directia axei Ox cat si in directia axei Oy.
Cele doua deplasari se noteaza prin u = u(x, y) si v = v(x,
y).
Intre deplasarile u si v si deplasarile εx si εy, ca si in starea lineara, exista relatiile:
![]()
![]() (42)
(42)
Din placa considerata se izoleaza elementul MACB (fig.14). Prin deformarea placii elementul se deplaseaza si se deformeaza.
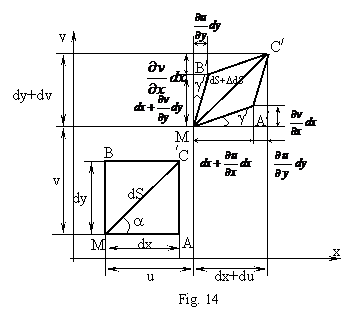
Daca deplasarea punctului M in directia axei Ox este u, atunci
deplasarea punctului A in directia aceleiasi axe este ![]() . Deplasarea punctului C in directia axei Ox va fi
. Deplasarea punctului C in directia axei Ox va fi ![]() .
.
Punctul C are si o deplasare in directia axei Oy care va fi:
![]() .
.
Totodata, in procesul de deformare, unghiul drept dintre laturile MB si MA se modifica cu cantitatea:
![]()
care reprezinta de fapt lunecarea specifica.
Diagonala MC are inainte de deformare lungimea: ![]() ,
,
iar dupa deformare:
(![]()
![]() )2=(
)2=(![]()
![]() )2 + (
)2 + (![]()
![]() )2
)2
adica,
(![]()
![]() )2=
)2=![]()
Se ridica la patrat parantezele, se neglijeaza infinitii mici de ordin superior si apoi prin impartire cu ds2 va rezulta expresia lungirii specifice in lungul diagonalei MC:
![]()
Inlocuid,
![]() , va rezulta :
, va rezulta :
![]()
sau in functie de unghiul dublu:
![]() (43)
(43)
Relatia obtinuta este de aceeasi forma cu relatia (1) a tensiunilor unde locul deformatiilor specifice liniare si unghiulare este luat de tensiunile normale si tangentiale. Prin analogie cu teoria eforturilor, se poate afirma ca exista in plan doua directii principale perpendiculare in lungul carora deformatiile specifice liniare sunt extreme, iar cele unghiulare sunt nule. Aceste directii coincid cu directiile tensiunilor principale, ele determinandu-se cu relatia:
![]() (44)
(44)
Deformatiile specifice liniare principale sunt date de relatia:
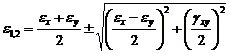 (45)
(45)
![]()
![]()
![]() Rezultatele
obtinute pentru starea plana de deformatii, pot fi extinse
si la starea spatiala . Astfel celor trei deplasari u, v
si w ale unui punct in directiile axelor de coordonate, le corespund
deformatiile specifice liniare:
Rezultatele
obtinute pentru starea plana de deformatii, pot fi extinse
si la starea spatiala . Astfel celor trei deplasari u, v
si w ale unui punct in directiile axelor de coordonate, le corespund
deformatiile specifice liniare:
si lunecarile specifice in trei plane perpendiculare paralele sistemului de referinta:
![]() (47)
(47)
Cunoscand cele noua componente ale tensorului deformatiilor
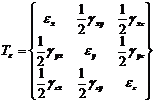 (48)
(48)
in care,
![]() ;
; ![]() ;
; ![]() ,
,
se pot determina
directiile principale ale deformatiilor liniare specifice precum
si valorile ![]() ,
, ![]() ,
, ![]() , ale acestora. Se poate de asemenea arata ca
lunecarile specifice au valori extreme in plane inclinate cu 45o
fata de directiile principale ale deformatiilor specifice
liniare, acestea fiind:
, ale acestora. Se poate de asemenea arata ca
lunecarile specifice au valori extreme in plane inclinate cu 45o
fata de directiile principale ale deformatiilor specifice
liniare, acestea fiind:
![]() ;
; ![]() ;
; ![]() (49)
(49)
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |