
MODELAREA COMPORTARII IN FUNCTIONARE A INSTALATIILOR TEHNOLOGICE CU AJUTORUL LANTURILOR MARKOV
1. Sistemul de ecuatii asociat unui proces stocastic de tip Markov
Conceptele centrale ale modelarii markoviene sunt cele de stare si tranzitie. Un sistem tehnic sau un element component se poate afla la un moment dat in una din urmatoarele stari: functionare, avarie, rezerva etc.
Starea unui sistem se poate modifica in timp, sistemul evoluand de la a stare la alta. Asemenea modificari ale starilor unui sistem se numesc tranzitii.
Procesul stochastic este determinat de o familie de variabile aleatoare si corespunde ca model matematic unui proces empiric a carui dezvoltare in viitor este guvernata de legi probabilistice.
Procesul Markov este un proces aleatoriu definit de o familie de variabile aleatoare.
Cunoasterea starilor sistemului la momentele succesive (t1, t2, .. tn,), anterioare momentului (t), prin preluarea si prelucrarea unor informatii care privesc starile anterioare, contribuie la cunoasterea sistemului la momentul (t).
Lantul Markov, este un proces Markov definit de
variabilele definit de variabilele , ![]() .
.
Cunoasterea starilor sistemului la
momentele consecutive ![]() anterioare lui t,
prin preluarea si prelucrarea unor informatii care privesc starile anterioare, contribuie
la cunoasterea starii la momentul t, prin furnizarea unor
informatii colectate din starile anterioare insa cuprinse toate
in starea cea mai recenta, respectiv starea corespunzatoare
momentului tn.
anterioare lui t,
prin preluarea si prelucrarea unor informatii care privesc starile anterioare, contribuie
la cunoasterea starii la momentul t, prin furnizarea unor
informatii colectate din starile anterioare insa cuprinse toate
in starea cea mai recenta, respectiv starea corespunzatoare
momentului tn.
Procesul Markov este un proces aleatoriu definit de o familie de variabile aleatoare.
Lantul Markov este
un proces Markov, definit de variabilele aleatoare ![]() care pot lua numai
valori apartinand unui sir infinit sau finit, in mod
conventional putandu-se considera pentru sir infinit sirul
numerelor naturale sau in caz finit sirul 1,2,3N.
care pot lua numai
valori apartinand unui sir infinit sau finit, in mod
conventional putandu-se considera pentru sir infinit sirul
numerelor naturale sau in caz finit sirul 1,2,3N.
Caracteristica procesului de a putea evolua intr-un sir finit sau infinit de stari ne conduce la lanturi Markov cu un numar finit de stari sau la lanturi Markov cu un numar infinit de stari.
Un proces stochastic ![]() este denumit proces
Markov multiplu de ordin i daca satisface pentru orice sir
finit
este denumit proces
Markov multiplu de ordin i daca satisface pentru orice sir
finit ![]() de valori ale
parametrului t conditia aleatoare
de valori ale
parametrului t conditia aleatoare ![]() depinde numai de
ultimule i variabile anterioare:
depinde numai de
ultimule i variabile anterioare:
Fiabilitatea elementului simplu reparabil
Pentru exemplificare se va studia cazul unui singur element pe care il consideram ca evolueaza din starea de functionare in starea de defect si invers (fig.1).
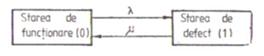
Fig. 1. Evolutia unui element din starea de functionare in starea de defect si invers
Se fac urmatoarele precizari:
- defectarea elementului considerat este un eveniment al carui
probabilitate de realizare intr-un interval Δt este ![]() , respectiv:
, respectiv:
|
|
- repararea, respectiv readucerea in starea initiala este un
eveniment a carui probabilitate in intervalul Δt este ![]() , respectiv:
, respectiv:
|
|
- probabilitatea ramanerii in stare de functionare:
|
|
- probabilitatea ramanerii in stare de reparare:
|
|
In acest context se va urmari evolutia elementului in intervalul infinitezimal de timp Δt, considerand:
- probabilitatea ca elementul sa fie in stare de functionare la
timpul t este ![]() ;
;
- probabilitatea ca elementul sa defect la timpul t este ![]() ;
;
- intensitatea de defectare este λ;
- intensitatea de reparare este μ.
Sistemul se afla in stare de functionare
la momentul ![]() cu probabilitatea
absoluta
cu probabilitatea
absoluta ![]() . Aceasta stare se poate obtine din
urmatoarele tranzitii de la (t) la
. Aceasta stare se poate obtine din
urmatoarele tranzitii de la (t) la ![]() :
:
- din starea 0 de functionare [probabilitatea ![]() ] tot in starea de functionare 0 [probabilitatea
] tot in starea de functionare 0 [probabilitatea ![]() ];
];
- din starea 1 de nefunctionare [probabilitatea ![]() ] in starea de functionare 0 [probabilitatea
] in starea de functionare 0 [probabilitatea ![]() ];
];
Conform relatiei (9.21)
rezulta daca se are in vedere evolutia elementului in intervalul
de timp Δt, adica sa determinam probabilitatea
absoluta ![]() se poate scrie:
se poate scrie:
|
|
Sistemul se afla in stare de nefunctionare
la momentul ![]() cu probabilitatea
absoluta
cu probabilitatea
absoluta ![]() (membrul drept al
relatiei (21). Aceasta stare se poate obtine din
urmatoarele tranzitii de la (t) la
(membrul drept al
relatiei (21). Aceasta stare se poate obtine din
urmatoarele tranzitii de la (t) la ![]() :
:
- din starea 0 de functionare [probabilitatea ![]() ] in starea de nefunctionare 1 [probabilitatea
] in starea de nefunctionare 1 [probabilitatea ![]() ];
];
- din starea 1 de nefunctionare [probabilitatea ![]() ] tot in starea de functionare 1[probabilitatea
] tot in starea de functionare 1[probabilitatea ![]() ];
];
Conform relatiei (9.21)
rezulta daca se are in vedere evolutia elementului in intervalul
de timp dt, adica sa determinam probabilitatea
absoluta ![]() se poate scrie:
se poate scrie:
|
|
Rezulta sistemul de ecuatii:
|
|
Grupand termenii acestui sistem si impartind cu Δt se obtine:
|
|
Punand conditia ![]() se obtine
sistemul de ecuatii diferentiale atasat unui proces Markov
finit, omogen, cu timp continuu:
se obtine
sistemul de ecuatii diferentiale atasat unui proces Markov
finit, omogen, cu timp continuu:
|
|
Sistemul de ecuatii obtinut poate fi scris sub forma matriciala:
|
|
sau sub forma generalizata:
|
|
unde ![]() reprezinta
probabilitatile absolute iar qij reprezinta
matricea de tranzitie ale carei elemente satisfac relatiile:
reprezinta
probabilitatile absolute iar qij reprezinta
matricea de tranzitie ale carei elemente satisfac relatiile:
|
|
Matricea de tranzitie ![]() este o matrice
patratica, singulara, ai carei termeni sunt
intensitati de tranzitie si are urmatoarele
proprietati:
este o matrice
patratica, singulara, ai carei termeni sunt
intensitati de tranzitie si are urmatoarele
proprietati:
- matricea contine termeni pozitivi sau nuli pentru i≠ j si reprezinta probabilitati;
- suma termenilor fiecarei coloane este egal cu zero.
Prin urmare sistemul de ecuatii diferentiale atasat unui proces Markov finit, simplu, cu timp continuu.
Pentru rezolvarea sistemului
de ecuatii diferentiale, pentru calculele ingineresti putem
sa ne limitam la un sistem de ecuatii algebrice in ![]() . Algebrizarea poate fi realizata considerand ca la
. Algebrizarea poate fi realizata considerand ca la
![]() probabilitatile absolute tind
sa devina independente de starea initiala si pot fi
considerate constante, ceea ce conduce la
probabilitatile absolute tind
sa devina independente de starea initiala si pot fi
considerate constante, ceea ce conduce la ![]() iar sistemul de
ecuatii diferentiale devine:
iar sistemul de
ecuatii diferentiale devine:
|
|
Produsul matricei
patratice si a matricei coloana conduce la rezolvarea unui
sistem algebric compatibil nedeterminat, nedeterminare ce se ridica prin
introducerea ecuatiei suplimentare ![]() , provenita din
, provenita din ![]() ,
, ![]() fiind probabilitatea
absoluta de stare, conditie care rezulta si din
considerarea unui camp complet de evenimente.
fiind probabilitatea
absoluta de stare, conditie care rezulta si din
considerarea unui camp complet de evenimente.
Prin urmare, pentru un element simplu, sistemului de ecuatii diferentiale trebuie sa i se adauge ecuatia mentionata. Rezulta:
|
|
Conditiile initiale sunt:
|
|
sau:
|
|
dupa cum sistemul s-a aflat initial in starea 0 sau in starea 1.
Pentru rezolvarea sistemului (14) se poate utiliza transformata Laplace ale carei proprietati mai importante sunt:
|
|
|
|
|
|
|
|
Utilizand transformata Laplace in rezolvarea sistemului se obtine (s-au utilizat conditiile initiale (15):
|
|
Avand in vedere conditiile initiale se poate scrie:
|
|
Solutiile (in operational) ale sistemului sunt:
|
|
Efectuand trecerea in domeniul real rezulta solutiile:
|
|
Particularizand prin trecere la limita pentru ![]() se obtin
probabilitatile absolute, independente de timp:
se obtin
probabilitatile absolute, independente de timp:
|
|
Trecand la limita
ecuatiile sistemului algebric de ecuatii diferentiale
rezulta ca ![]()
si ![]() verifica sistemul
algebric:
verifica sistemul
algebric:
|
|
In cazul in care exista mai mult de doua stari, probabilitatile absolute de stare verifica sistemul:
|
|
3. Calculul indicatorilor de fiabilitate ai elementului simplu reparabil
a) Analiza tranzitiilor dintre stari
Graficul tranzitiilor pentru un element simplu reparabil, daca notam cu "0" starea de functionare si cu "1" starea de defect este aratata in fig. 1.
b) Scrierea matricei intensitatilor de tranzitie ![]()
Matricea ![]() este o matrice
patrata cu dimensiunea data de numarul starilor:
este o matrice
patrata cu dimensiunea data de numarul starilor:
|
| |||
|
|
|
||
|
|
|
c) Scrierea ecuatiei matriceale si rezolvarea ei
|
|
respectiv:
|
|
din care rezulta ecuatiile:
|
|
Solutiile sistemului sunt:
|
|
c) calculul indicatorilor de fiabilitate:
- Probabilitatea de succes si refuz
|
|
- Timpul mediu total probabil de succes:
|
|
- Timpul mediu total probabil de refuz:
|
|
- Numarul mediu probabil de avarii:
|
|
- Timpul mediu de functionare:
|
|
Timpul mediu de reparare:
|
|
|
Politica de confidentialitate |
| Copyright ©
2026 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| MODELAREA COMPORTARII IN FUNCTIONARE A INSTALATIILOR TEHNOLOGICE CU AJUTORUL LANTURILOR MARKOV |
| Sisteme de ecuatii si transformari liniare. (Regula lui Cramer) |
| Termeni si conditii |
| Contact |
| Creeaza si tu |