
Cel mai mare dezastru al secolului douazeci a fost prabusirea bursiera din 1929 si Marea Criza care a urmat-o. Al doilea a fost piata in scadere si recesiunea din 1973-1974. Aceasta din urma nu a inceput intr-o zi nefasta, asa cum s-a intamplat in 1929, iar efectele sale asupra familiilor americane nu au fost atat de raspandite si devastatoare si, prin urmare, nu ocupa acelasi loc in memoria colectiva. Totusi, pentru profesionistii financiari, a doua perioada este aproape la fel de importanta, pentru ca reprezinta un moment critic in istoria finantelor moderne si in special in dezvoltarea teoriei portofoliului de titluri.
Piata in scadere din 1973-1974 a fost un proces incet, sinuos de pierderi severe care au durat doi ani neintrerupti. Pietele mai mari au scazut cu peste 60%. Cei care aveau venituri fixe si obligatiuni cu cupoane si-au vazut investitiile micsorandu-se. Ratele dobanzii si inflatiei au crescut pana la doua cifre. Preturile la petrol au crescut vertiginos. Preturile la locuinte erau atat de ridicate incat foarte putine familii cu venit mediu isi puteau permite sa cumpere o casa noua. A fost o perioada grea, intunecata.
Atat de mare a fost dezastrul financiar incat managerii de investitii au inceput sa-si puna la indoiala propria abordare. Cautand raspunsuri, cei mai multi profesionisti in investitii s-au indreptat treptat, unii dintre ei cu o mare indoiala, spre o serie de studii academice care au fost in mare masura ignorate timp de doua decenii. In mod unanim, aceste studii academice au ajuns sa fie denumite teorii moderne ale portofoliului.
In martie 1952, a aparut in "The Journal of Finance" un articol
intitulat "Selectia portofoliului" de Harry Markowitz, un absolvent al
Universitatii din
Din punctul de vedere al lui Markowitz nu era nevoie de volume intregi pentru a explica ceea ce el considera o notiune foarte simpla: castigul si riscul sunt inseparabile. Ca economist credea ca este posibila determinarea relatiei dintre castig si risc pana la un grad statistic real si, astfel, sa se determine gradul de risc care ar fi necesar pentru diferite niveluri de castig. In articolul sau el a prezentat calculele care sustineau concluzia cǎ nici un investitor nu poate avea beneficii peste medie fara sa-si asume un risc corespunzator.
Markowitz a remarcat mai tarziu: "Am fost uimit de faptul ca trebuie sa fii interesat si de risc si de castig in aceeasi masura." Desi astazi aceasta declaratie pare uimitor de evidenta in lumina a ceea ce am invatat despre investitii, in anii '50 era un concept revolutionar. Pana la acea vreme, investitorii au acordat foarte putina atentie managementului portofoliului si notiunii de risc. Portofoliile erau concepute oarecum la intamplare. Daca un manager considera ca pretul unei actiuni urma sa creasca, era pur si simplu adaugata portofoliului. Nu era nevoie de nici un rationament.
Aceasta l-a nedumerit pe Markowitz. El a considerat ca este necugetata ideea potrivit careia se pot realiza castiguri mari fara expunerea la un anumit risc. Pentru a clarifica aceste idei, Markowitz a creat ceea ce el a numit "frontiera de eficienta". El a explicat: "Fiind economist, am realizat un grafic in contrapartida: riscul pe o axa si castigul prognozat pe cealalta. Frontiera eficientei este o simpla dreapta trasata din stanga jos spre dreapta sus. Fiecare punct de pe aceasta dreapta reprezinta intersectia dintre castigul potential si nivelul sau de risc. Un portofoliu ineficient este acela care expune investitorul la un nivel de risc fara sa ofere un nivel corespunzator al castigului. Obiectivul managerilor de investitii este sa realizeze portofolii corespunzator nivelului de risc tolerat de investitori si, in acelasi timp, sa limiteze si sa evite portofoliile ineficiente."
In 1959 Markowitz a publicat prima sa carte, "Portofolio Selection: Efficient Diversification of Investment", bazata pe teza sa de doctorat. In aceasta el a descris mai detaliat ideile sale despre risc, folosind abaterea standard pentru a masura riscul. Abaterea poate fi considerata ca distanta fata de medie. Conform lui Markowitz, riscul este mai mare cu cat distanta fata de medie este mai mare.
S-ar putea crede ca riscul unui portofoliu, asa cum a fost definit de Markowitz, este pur si simplu media abaterilor standard ale actiunilor individuale din portofoliu. Dar, astfel, se omite un punct important. Desi abaterea poate oferi o masura a riscului unei actiuni individuale, media a doua abateri (sau a o suta de abateri) va oferi foarte putine informatii despre riscul portofoliului format din cele doua actiuni (sau din o suta de actiuni).
Ceea ce si-a facut Markowitz a fost sa gaseasca o modalitate de a determina riscul intregului portofoliu. Aceasta este considerata de multi marea sa contributie. El a numit-o "covariatie" care masoara tendinta unui grup de actiuni. Spunem ca doua actiuni au covariatie mare cand preturile lor, indiferent de motiv, tind sa evolueze in acelasi sens. Dimpotriva, covariatia slaba este atunci cand doua actiuni se misca in directii opuse. In conceptia lui Markowitz riscul unui portofoliu nu este dat de variatia actiunilor individuale, ci de covariatia tuturor actiunilor. Cu cat acestea variaza in acelasi sens, cu atat este mai mare probabilitatea ca schimbarile economice sa conduca la scaderea lor in acelasi timp. Un portofoliu mai putin riscant poate fi, deci, o selectie de actiuni ale cǎror preturi individuale evolueazǎ in sensuri diferite. Oricum, potrivit lui Markowitz, cheia este diversificarea.
In conceptia lui Markowitz, urmatorul pas pe care trebuie sa-l faca un investitor este sa identifice nivelul de risc pe care este dispus sa-l accepte si apoi sa construiasca un portofoliu diversificat, eficient, din actiuni cu covariatie slaba.
Cartea lui Markowitz, ca si articolul original, au fost ignorate de profesionistii in investitii, datorita complexitatii calculelor ce trebuiau efectuate. Cu toate acestea, lumea academica considera ca aceste lucrari reprezinta punctul de pornire in teoria financiara moderna.
Majoritatea celor ce investesc pe piata de capital prefera detinerea mai multor valori mobiliare in raport cu detinerea unei valori mobiliare, intrucat, in general, includerea mai multor valori mobiliare intr-un portofoliu reduce riscul total in raport cu riscul individual al fiecarui titlu. Cele mentionate sugereaza ca atractivitatea nu rezida in mod exclusiv in castigurile prognozate. Daca acestea din urma ar fi singurul determinant al investitiilor pe piata, investitorii ar plasa toate resursele disponibile in acea valoare mobiliara care ofera cel mai mare castig prognozat.
Cea mai semnificativa contributie adusa de Markowitz este analiza implicatiilor faptului ca investitorii, cautand realizarea de castiguri prognozate ridicate, tind in general sa evite riscul. Avand in vedere faptul ca aversiunea fata de risc caracterizeaza majoritatea investitorilor si in special investitorii institutionali, un management rational al portofoliului reclama luarea in considerare nu numai a castigurilor prognozate pentru un portofoliu, dar si a riscului pe care acel portofoliu in presupune.
Desi castigul prognozat al unui portofoliu este in mod direct corelat cu castigurile prognozate ale valorilor mobiliare componente, nu este posibil de dedus riscul unul portofoliu prin simpla cunoastere a riscului fiecarei valori mobiliare. Riscul unui portofoliu depinde nu numai de atributele fiecarei valori mobiliare considerate individual, ci si de interdependentele existente intre acestea. Datorita acestei argumentatii, managementul portofoliului reprezinta un subiect aparte al studierii pietei de capital.
Un alt motiv pentru care managementul portofoliului este abordat separat constǎ in faptul ca acesta depinde de nevoile si preferintele investitorilor individuali. Este posibila estimarea castigurilor prognozate pentru anumite valori mobiliare fara a se face raportarea la investitorii individuali, dar este imposibila constituirea unui portofoliu care sa fie considerat optim pentru un investitor individual fara a fi luate in calcul nevoile si preferintele sale. Rezultatele analistului financiar pe piata de capital sunt determinante pentru managementul portofoliului, dar managerii utilizeaza calculele analistului financiar numai in corelatie cu preferintele si situatia financiara ale investitorilor individuali. In acest context, cu toate ca analiza financiara este impersonala, managementul portofoliului incumba in mod obligatoriu o latura personalǎ.
Teoria portofoliului dezvoltata de Markowitz este construita in jurul urmatoarelor idei centrale: cele doua caracteristici relevante ale unui portofoliu sunt castigul prognozat si riscul sau; investitorii rationali vor prefera detinerea de portofolii eficiente, care maximizeaza castigurile prognozate la un anumit nivel al riscului sau, in mod alternativ ori echivalent, minimizeaza riscul la un nivel dat al castigului prognozat; este posibila identificarea portofoliilor eficiente prin analiza temeinica a informatiilor pentru fiecare valoare mobiliara (castigul prognozat, oscilatiile castigului prognozat, relatiile dintre castigul pentru fiecare valoare mobiliara si castigurile celorlalte valori mobiliare); existenta unui program computerizat care utilizeaza drept input-uri calculele analistului financiar (informatiile necesare pentru fiecare valoare mobiliara cu scopul de a constitui un portofoliu eficient). Programul indica ponderea resurselor financiare ale investitorului care ar trebui alocata pentru fiecare valoare mobiliara pentru ca portofoliul sa fie eficient.
Notiunea de portofolii eficiente este ilustrata in figura 1 (expected return - castig prognozat, risk - risc).
Figura 1. Frontiera de eficienta ipotetica
|
|
Axa verticala (ordonata) masoara castigul prognozat al unui portofoliu, iar axa orizontala (abscisa) masoara riscul asociat portofoliului. Aria hasurata reprezinta toate portofoliile posibile care pot fi obtinute pe baza anumitor valori mobiliare. Portofoliul aflat de-a lungul curbei ABC este eficient intrucat ofera maximizarea castigului la un anumit nivel al riscului sau minimizarea riscului la un anumit nivel al castigului. La nivelul punctului D, portofoliul se afla la limita de fezabilitate, dar nu este eficient, intrucat portofoliul aflat de-a lungul curbei ABC, care ofera acelasi castig prognozat, este mai putin riscant. Analize similare pot fi intreprinse pentru toate portofoliile aflate in cadrul ariei hasurate.
Studiile lui Markowitz se bazeaza pe presupunerea ca orice investitor rational va prefera portofoliile eficiente in raport cu celelalte portofolii. Optiunea unui investitor pentru un anumit portofoliu in raport cu altele - inclusiv in raport cu altele eficiente - depinde de nevoile si optiunile sale. Cu alte cuvinte, alegerea este influentata de functia de utilitate a investitorului.
In cele ce urmeaza va fi analizata relatia dintre un portofoliu si valorile mobiliare ce il compun. In primul rand trebuie abordata relatia dintre castigul unui portofoliu si castigurile valorilor mobiliare componente. In acest sens, castigul unui portofoliu este suma ponderata a castigurilor valorilor mobiliare componente, ponderea fiecarei valori mobiliare fiind procentul din valoarea totala a portofoliului care este investita in respectivul titlu. Sa presupunem ca 100 lei sunt investiti in trei valori mobiliare.
Tabelul 1. Calculul castigului prognozat al unui portofoliu
|
Valoarea mobiliara |
Ponderea investita (Xi) |
Castigul prognozat (Ri) |
XiRi |
|
1 |
0,5 |
0,10 |
0,050 |
|
2 |
0,3 |
0,20 |
0,060 |
|
3 |
0,2 |
0,05 |
0,010 |
|
Total |
1,0 |
0,120 |
![]()
Rp = castigul prognozat al portofoliului (XiRi)
In acest caz:
Survin insǎ dificultǎti, intrucat managerii de portofolii sunt preocupati de castigurile viitoare. In cazul in care castigurile anumitor valori mobiliare ar fi cunoscute cu precizie, castigul oricarui portofoliu ar fi previzionat cu acuratete, iar randamentele tuturor valorilor mobiliare ar fi egale. Avand in vedere faptul ca viitorul nu este cert, managerii de portofolii trebuie sa-si fundamenteze selectiile pe prognoze ale castigurilor. Sa presupunem ca un analist a efectuat urmatoarea previziune pentru o anumita valoare mobiliara.
Tabelul 2. Prognoza castigurilor
|
Castiguri |
Probabilitate |
|
8% |
Foarte posibil |
|
5% |
Posibil, dar improbabil |
|
12% |
Posibil, dar improbabil |
Prognoza de 8% este cea mai buna estimare a analistului, dar acesta nu poate fi sigur. Pentru adancirea prognozei, pot fi efectuate calcule suplimentare ce vor fi reflectate cu ajutorul histogramei. In figura 2, pe orizontala sunt reprezentate mijloacele intervalelor (probability - probabilitate, rate of return - castig prognozat). Astfel, 5 inseamna cel putin 4,5 si cel mult 5,5.
Figura 2. Prognoza analistului privind castigurile posibile
pentru valoarea mobiliara A
|
|
Aceasta distributie reflecta probabilitatile ca titlul sa ofere anumite castiguri intr-o perioada determinata de timp. In mod normal, probabilitatile trebuie sa se rezume la una.
In exemplul de mai sus, cu o probabilitate de 0,05 venitul asteptat va fi de 5% sau de 12%, sau cu o probabilitate de 0,25 venitul asteptat va fi de 8%. Castigul prognozat sau sensul distributiei (normala, platicurtica, leptocurtica) este egal cu suma ponderata a castigurilor posibile, ponderile fiind reprezentate de probabilitati. In acest caz, castigul mediu sau asteptat este de 8,3%. Astfel, castigul asteptat al unui portofoliu poate fi definit ca suma ponderata a castigurilor asteptate ale valorilor mobiliare individuale.
Insa, relatiile dintre estimarile riscului fiecarei valori mobiliare si estimarile riscului unui portofoliu sunt complexe. Pentru aprecierea riscului vom utiliza dispersia variabilei care se calculeaza ca medie a patratelor abaterilor individuale absolute de la media repartitiei. Radacina patrata a dispersiei este cunoscuta sub denumirea de abatere standard. In cazul distributiei normale (curba lui Gauss), aceasta este crescatoare. Probabilitatile ca un castig sa se incadreze in intervalul valoarea asteptata (E) plus sau minus abaterea standard (as) sunt de aproximativ 2 din 3. Probabilitatile ca un castig sa se incadreze in intervalul E+2as - E-2as sunt de aproximativ 95 din 100. Aceste afirmatii sunt valabile doar pentru distributia normala. Cu toate acestea, abaterea standard este un indicator sintetic util pentru aprecierea gradului de imprastiere in raport cu valoarea asteptata. In cadrul estimarilor, dispersia variabilei este mult mai utilizata in raport cu abaterea standard, dar rezultatele sunt de regula exprimate in termenii celei din urma. In timp ce abaterea standard pe fiecare dolar investit nu se schimba odata cu suma investita, dispersia pe fiecare dolar investit creste odata cu suma investita. Portofoliile care sunt eficiente din punct de vedere al dispersiei variabilei sunt eficiente si din punct de vedere al abaterii standard si vice versa.
Desi castigul asteptat al unui portofoliu este suma ponderata a castigurilor asteptate ale valorilor mobiliare componente, dispersia unui portofoliu nu este calculata ca suma ponderata a dispersiilor valorilor mobiliare componente. Desigur, dispersia fiecarei valori mobiliare se constituie intr-un factor de influenta, dar este necesara cunoasterea interdependentelor existente intre oscilatiile castigurilor prognozate ale valorilor mobiliare componente.
Prin urmatoarele exemple se va demonstra logic veridicitatea celor expuse. Toate aceste exemple se refera la portofolii care includ doar doua valori mobiliare, dar principiile sunt valabile si pentru acele portofolii care includ mai mult de doua valori mobiliare. Totodata, pentru simplificarea explicatiei se va presupune ca valorile mobiliare din portofoliu nu sunt purtatoare de dividende sau dobanzi. De aceea, oscilatiile preturilor valorilor mobiliare sunt determinate numai de castigurile prognozate. Prin urmare, graficele se refera la oscilatiile in timp ale preturilor (Time = timp, Change in Price = modificarea pretului, security = actiune, portofolio = portofoliu).
|
Figura 3. Schimbarile procentuale ale preturilor valorilor mobiliare i si j (corelatia = 1,0) |
|
|
In primul exemplu, evolutia celor doua valori mobiliare este identica. Cu toate ca amplitudinile oscilatiilor preturilor sunt diferite, schimbarile pretului sunt perfect corelate, ceea ce inseamna ca se poate determina cu maxima precizie oscilatia pretului unei valori mobiliare pe baza cunoasterii oscilatiei pretului celeilalte valori mobiliare. In acest exemplu, corelatia este pozitiva (cand pretul valorii mobiliare i creste sau scade cu 1%, pretul valorii mobiliare j creste sau scade cu 0,5%). Daca se presupune ca in cele doua valori s-a investit initial aceeasi suma, valoarea intregului portofoliul creste sau scade cu 0,75%. Pe baza formulei dispersiei, rezulta ca dispersia portofoliului este de 3,1%, dispersia valorii mobiliare i este 5,5%, iar cea a valorii mobiliare j este 1,4%.
Si in al doilea exemplu, evolutia celor doua valori mobiliare este identica, dar directiile in care evolueaza sunt diferite. Cand pretul valorii mobiliare i creste cu 1%, pretul valorii mobiliare j scade cu 0,5% si viceversa. Daca se presupune ca in cele doua valori s-a investit initial aceeasi suma, valoarea intregului portofoliul creste sau scade cu 0,25%, spre deosebire de oscilatia de 0,75% din exemplul anterior. Dispersiile pentru valoarea mobiliara i, j si pentru intreg portofoliu sunt de 5,5%, 1,4% si 0,3%. In acest exemplu, daca dispersiile celor doua valori mobiliare ar fi identice, oscilatiile pretului valorii mobiliare i ar fi perfect compensate de oscilatiile pretului valorii mobiliare j si dispersia portofoliului ar fi 0.
|
Figura 4. Schimbarile procentuale ale preturilor valorilor mobiliare i si j (corelatia = -1,0) |
|
|
|
Figura 5. Schimbarile procentuale ale preturilor valorilor mobiliare i si j (corelatie pozitiva, mai mica decat 1) |
|
|
Cel ce-al treilea exemplu este mult mai realist. In acest sens, preturile celor doua valori mobiliare sunt corelate intr-o anumita masura, dar nu cunosc o evolutie identica, ceea ce este valabil pentru majoritatea valorilor mobiliare incluse la cota bursei. Cand actiunile cresc sau scad perfect identic, diversificarea nu reduce dispersia portofoliului, intrucat fluctuatiile fiecarei valori mobiliare nu sunt compensate. Cand oscilatiile sunt contrare, compensarea este maximizata, ca de altfel si efectul diversificarii asupra diminuarii dispersiei. Cand corelatia nu este perfecta (este cuprinsa intre ±1), fluctuatiile valorilor mobiliare sunt compensate partial. De aceea, diversificarea este indispensabil conexata de reducerea riscului calculat prin intermediul dispersiei castigului portofoliului.
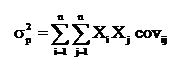
Dispersia portofoliului este calculata prin urmatoarea formula: ![]() , unde: covij = codispersia dintre
castigurile prognozate ale valorilor i
si j;
, unde: covij = codispersia dintre
castigurile prognozate ale valorilor i
si j; ![]() = dispersia
castigului prognozat al valorii
mobiliare i;
= dispersia
castigului prognozat al valorii
mobiliare i; ![]() = dispersia
castigului prognozat al valorii
mobiliare j; Xi = ponderea investita in valoarea mobiliara i; Xj =
ponderea investita in valoarea mobiliara j.
= dispersia
castigului prognozat al valorii
mobiliare j; Xi = ponderea investita in valoarea mobiliara i; Xj =
ponderea investita in valoarea mobiliara j.
In cazul a n valori mobiliare formula devine:
In formula anterioara, covii (i=i, j=i) este egala cu dispersia lui i.
Cu toate ca formula se refera la un portofoliu alcatuit numai din doua valori mobiliare, aceasta se caracterizeaza prin grad ridicat de generalizare, intrucat pachetele de valori mobiliare pot fi abordate ca o singura valoare mobiliara in analiza problemelor de management ale portofoliului. De exemplu, daca se doreste cunoasterea implicatiilor includerii unei noi valori mobiliare in cadrul unui portofoliu asupra dispersiei portofoliului, portofoliul existent poate fi considerat drept o singura valoare mobiliara.
Codispersia reflecta gradul in care doua valori mobiliare evolueaza sau nu corelat. Aceasta notiune are un sens matematic precis ilustrat in figura 6. Prima diagrama indica relatiile din castigurile prognozate ale valorilor mobiliare i si j in patru momente diferite. Dreapta reflecta relatiile medii pentru aceste patru momente. Aceasta a fost trasata astfel incat distantele patratelor aflate pe verticala fata de dreapta sa fie minimizate si sa reprezinte o estimare a dreptei de regresie (Deviation from regression line).
De asemenea, este posibila cuantificarea abaterilor punctelor fata de castigul mediu prognozat al valorii mobiliare j. Aceasta este ilustrata in cel de-al doilea grafic al figurii 6. Dispersia totala a castigului prognozat al valorii mobiliare j (media abaterilor - Deviation from Mean) este in acest fel compusa din doua parti: cea atribuita abaterilor de la dreapta de regresie si cea atribuita dispersiei castigului prognozat al valorii mobiliare i sau factorilor care genereaza dispersia.
Figura 6. Relatiile dintre castigurile prognozate ale
valorilor mobiliare i si j
|
|
|
|
O apreciere
cantitativa a gradului in care preturile a doua valori mobiliare
oscileaza corelat este data de urmatoarea formula
(coeficientul de corelatie 0<p<1): 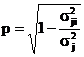 unde:
unde: ![]() = dispersia
castigului prognozat al valorii mobiliare j (dupa luarea in considerare a relatiei cu castigul
prognozat al valorii mobiliare i)sau
acea parte a dispersiei totale atribuita abaterilor de la dreapta de
regresie;
= dispersia
castigului prognozat al valorii mobiliare j (dupa luarea in considerare a relatiei cu castigul
prognozat al valorii mobiliare i)sau
acea parte a dispersiei totale atribuita abaterilor de la dreapta de
regresie; ![]() = dispersia
totala a castigului prognozat al valorii mobiliare j sau abaterile de la medie
= dispersia
totala a castigului prognozat al valorii mobiliare j sau abaterile de la medie
Dupa cum
indica formula, daca abaterile de la dreapta de regresie, ![]() , sunt egale cu abaterile de la medie, valoarea
corelatiei este zero. Cu alte cuvinte, cunoasterea dispersiei
castigului prognozat al valorii mobiliare i nu contribuie la
explicarea sau previzionarea dispersiei castigului prognozat al valorii
mobiliare j. Astfel, daca toate
punctele se afla pe dreapta de regresie, corelatia este egala cu
1. Coeficientul de corelatie liniara are valorile cuprinse in
intervalul ±1, cu urmatoarea semnificatie: valorile mai mici ca 0
evidentiaza faptul ca intre cele doua variabile exista
o corelatie inversa si este cu atat mai intensa cu cat
nivelul coeficientului este mai apropiat de -1; valorile mai mari ca 0
evidentiaza o corelatie directa a carei intensitate
creste pe masura ce nivelul coeficientului se apropie de 1.
, sunt egale cu abaterile de la medie, valoarea
corelatiei este zero. Cu alte cuvinte, cunoasterea dispersiei
castigului prognozat al valorii mobiliare i nu contribuie la
explicarea sau previzionarea dispersiei castigului prognozat al valorii
mobiliare j. Astfel, daca toate
punctele se afla pe dreapta de regresie, corelatia este egala cu
1. Coeficientul de corelatie liniara are valorile cuprinse in
intervalul ±1, cu urmatoarea semnificatie: valorile mai mici ca 0
evidentiaza faptul ca intre cele doua variabile exista
o corelatie inversa si este cu atat mai intensa cu cat
nivelul coeficientului este mai apropiat de -1; valorile mai mari ca 0
evidentiaza o corelatie directa a carei intensitate
creste pe masura ce nivelul coeficientului se apropie de 1.
Codispersia
dintre i si j este strans legata de corelatia dintre i si j, fiind calculata prin inmultirea raportului de
corelatie cu abaterea standard a lui i
si j. Este dificil de apreciat
corect valoarea absoluta a codispersiei intrucat aceasta depinde nu numai
de corelatia dintre i si j, dar si de amplitudinea
fluctuatiilor lui i si j. Prin urmare, formula codispersiei
devine: ![]() .
.
Pentru evidentierea modului in care diferitele valori ale codispersiei sau corelatiei afecteaza dispersia portofoliului, sa presupunem ca doua valori (valori mobiliare individuale sau portofolii) au aceleasi castiguri prognozate si dispersii, sumele investite fiind egale. Daca castigurile prognozate sunt de 5%, iar dispersiile de 2%, castigul prognozat al portofoliului este de 5%.
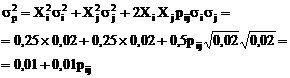
Aceasta ilustreaza semnificatia deosebita a interdependentelor dintre valorile mobiliare. Daca nu exista corelatie (p=0,0), dispersia portofoliului este de 1% sau mai putin decat a unui portofoliu investit in totalitate doar intr-una dintre valorile mobiliare.
Cand
corelatia este perfecta si pozitiva (p=1), dispersia
portofoliului este de 2%, aceeasi ca a valorilor mobiliare. Cand
corelatia este perfecta si negativa (p=-1), dispersia
portofoliului este 0. Cand corelatia este perfecta, expresia
dispersiei poate fi factoriala. In acest ultim caz, abaterea standard a
portofoliului este in dependenta liniara cu sumele investite in
fiecare valoare mobiliara. De exemplu, cand corelatia dintre i si j este perfecta si pozitiva, pij=1
dispersia portofoliului este: ![]() iar abaterea standard este:
iar abaterea standard este: ![]() .
.
Cand corelatia nu este perfecta, abaterea standard a portofoliului nu este o functie liniara a sumelor investite in fiecare valoare mobiliara. Intrucat investitorii evita riscurile si intrucat corelatia negativa sau codispersia dintre o valoare mobiliara si un portofoliu reduce dispersia unui portofoliu, asemenea valori mobiliare, daca exista, vor fi printre cele preferate. Pe de alta parte, valorile mobiliare care sunt strans corelate cu portofoliul nu contribuie la reducerea riscului care este scopul diversificarii. Intr-o situatie intermediara se afla acele valori mobiliare care inregistreaza o corelatie pozitiva (se apropie de 0) in raport cu celelalte valori mobiliare ale portofoliului. Un portofoliu constituit din doua valori mobiliare va avea o abatere standard mai mica decat a valorilor mobiliare individuale cand corelatia este mai redusa decat raportul dintre cea mai mica si cea mai mare abatere standard.
S-a demonstrat ca atractivitatea unui portofoliu este influentata atat de castigul sau prognozat, cat si de riscul pe care il presupune. Riscul, calculat prin intermediul dispersiei castigului prognozat al portofoliului, depinde de dispersiile valorilor mobiliare componente si de codispersia existenta intre acestea. In cele ce urmeaza se va analiza mai profund notiunea de portofoliu eficient. Diagrama de mai jos indica riscurile si castigurile prognozate a zece portofolii, fiecare fiind constituit dintr-o singura valoare mobiliara. Astfel, portofoliul 3 este preferat in raport cu portofoliul 1 intrucat ofera un castig mai mare in conditiile aceluiasi risc. In mod similar, portofoliul 1 este preferat in raport cu portofoliul 2, deoarece presupune un risc mai mic pentru acelasi castig. Daca valorile mobiliare nu sunt perfect corelate, ceea ce este valabil in acest exemplu, portofoliile constituite prin combinatiile acestor valori mobiliare pot inregistra dispersii mai reduse pentru anumite castiguri sau castiguri mai ample pentru anumite dispersii decat portofoliile formate dintr-o singura valoare mobiliara. De exemplu, portofoliul P poate reprezenta o combinare a portofoliilor 3 si 4.
Figura 7. Castigul prognozat si riscul portofoliilor
|
|
Pentru orice grup de valori mobiliare, multimea probabila de portofolii rezida in toate portofoliile alcatuite dintr-o singura valoare mobiliara si toate combinatiile posibile intre acestea. Acelea care sunt eficiente sunt plasate la limita superioara a multimii probabile. Aceasta limita este cunoscuta sub denumirea de frontiera de eficienta a portofoliilor formate din valori riscante si este reprezentata de curba ABC din figura 8 (expected return - castig prognozat, risk - risc.).
Figura 8. Multimea probabila si frontiera de eficienta
|
|
Frontiera de
eficienta va fi dispusa in semicerc (va avea forma concava).
De aceea, toate punctele de limita situate intre A si B vor fi
plasate pe sau deasupra dreptei care uneste cele doua puncte. Pentru
demonstrarea acestui fapt vom intocmi figura I.9. Portofoliile care
reprezinta combinari intre A si B vor avea valori ale lui E(Rp)
si ![]() care se
afla de-a lungul sau deasupra dreptei punctate AB. Daca
castigurile prognozate ale lui A
si B sunt perfect corelate, combinatiile se vor afla pe dreapta AB,
deoarece pentru orice combinari, atat castigurile, cat si
abaterea standard vor fi o functie liniara a sumelor investite in A
(sau in B). In cazul in care castigurile pentru A si B nu sunt
perfect corelate, combinatiile vor fi situate deasupra dreptei AB,
deoarece dispersiile si abaterile standard vor fi mai reduse atunci cand
corelatia nu este perfecta, iar combinatiile vor fi plasate
deasupra si in stanga dreptei AB. In orice caz, combinatiile vor fi
preferate portofoliilor aflate pe curba convexa (APB), care nu poate fi o
frontiera de eficienta.
care se
afla de-a lungul sau deasupra dreptei punctate AB. Daca
castigurile prognozate ale lui A
si B sunt perfect corelate, combinatiile se vor afla pe dreapta AB,
deoarece pentru orice combinari, atat castigurile, cat si
abaterea standard vor fi o functie liniara a sumelor investite in A
(sau in B). In cazul in care castigurile pentru A si B nu sunt
perfect corelate, combinatiile vor fi situate deasupra dreptei AB,
deoarece dispersiile si abaterile standard vor fi mai reduse atunci cand
corelatia nu este perfecta, iar combinatiile vor fi plasate
deasupra si in stanga dreptei AB. In orice caz, combinatiile vor fi
preferate portofoliilor aflate pe curba convexa (APB), care nu poate fi o
frontiera de eficienta.
Figura 9. Frontiera de eficienta posibila si imposibila
|
|
Figura 10. Castigul prognozat in functie de ![]() si
si ![]()
|
|
Cu toate
ca frontiera de eficienta poate fi liniara din punct de
vedere al lui E(Rp), ![]() , aceasta nu va fi liniara din punct de vedere al
E(Rp),
, aceasta nu va fi liniara din punct de vedere al
E(Rp), ![]() . Adancitura limitei E(Rp),
. Adancitura limitei E(Rp), ![]() va fi
intotdeauna mai proeminenta, ceea ce este ilustrat in figura 10. Dupa
cum s-a mentionat, multimea probabila va fi aceeasi atat
din punct de vedere al abaterii standard, cat si din punct de vedere al
dispersiei. Astfel, atunci cand se utilizeaza abaterea standard, frontiera
de eficienta va fi liniara intre A si B, in timp ce atunci
cand se utilizeaza dispersia, intreaga frontiera de
eficienta va fi concava.
va fi
intotdeauna mai proeminenta, ceea ce este ilustrat in figura 10. Dupa
cum s-a mentionat, multimea probabila va fi aceeasi atat
din punct de vedere al abaterii standard, cat si din punct de vedere al
dispersiei. Astfel, atunci cand se utilizeaza abaterea standard, frontiera
de eficienta va fi liniara intre A si B, in timp ce atunci
cand se utilizeaza dispersia, intreaga frontiera de
eficienta va fi concava.
In mod firesc, modelul lui Markowitz a fost extins pentru cazurile in care sunt constituite portofolii ce includ titluri care nu sunt purtatoare de risc, portofolii formate pe baza capitalurilor imprumutate, ca si portofolii formate din titluri riscante achizitionate pe baza dividendelor incasate de investitor.
Frontiera de eficienta a portofoliilor avand in componenta numeroase titluri riscante este de regula concava. Pentru orice perioada data de timp, pot fi identificate titluri ale caror castiguri pot fi previzionate cu aproximativ o maxima certitudine. Majoritatea investitorilor cred ca pot previziona cu maxima precizie, pentru orice perioada de timp, castigul prognozat al bonurilor de tezaur. Astfel, acesta din urma este egal cu maturitatea respectivelor titluri. De exemplu, bonurile de tezaur cu scadenta de un an au un castig previzibil precis pentru un an. Pentru acele bonuri de tezaur ce presupun plata periodica a dobanzilor, previzionarea castigului in raport cu maturitatea este intr-o oarecare masura mai putin certa intrucat castigurile ce rezulta prin reinvestirea dobanzilor nu pot fi cunoscute cu precizie.
Includerea titlurilor fara risc in portofolii are consecinte interesante. In urmatoarea diagrama castigul titlului fara risc este reprezentat de punctul Rf de pe ordonata. Daca aceasta alternativa exista, este posibila selectarea de portofolii in orice punct de pe dreapta RfB, definita prin castigul titlului fara risc si punctul de tangenta a portofoliilor formate din titluri riscante cu frontiera de eficienta, ceea ce decurge din argumentatia anterioara privind combinarea titlurilor.
Asa cum s-a evidentiat, castigul prognozat al unui portofoliu, format din doua titluri, A si B, este intotdeauna o functie liniara a sumelor investite in cele doua titluri. Formula dispersiei pentru acest tip de portofolii este urmatoarea:
![]()
Daca titlul fara risc este reprezentat de i, iar portofoliul format din titluri riscante in punctul de tangenta de catre j, se poate observa cu usurinta ca numai cel de-al doilea termen la ecuatiei are valoare pozitiva. Valoarea primului termen este zero, intrucat castigul titlului fara risc are dispersia zero, cel de-al treilea termen are valoarea zero intrucat castigul titlului fara risc are abaterea standard zero. De aceea, dispersia portofoliului este influentata in mod exclusiv de ponderea care este investita in titlul riscant sau, echivalent, de ponderea investita in titlul fara risc.
Daca ![]() , atunci
, atunci ![]() .
.
Cu alte cuvinte, riscul portofoliului calculat prin intermediul abaterii standard este in dependenta liniara cu ponderea investita in j (sau i). Este posibila investirea intregii sume atat in titlul fara risc, cat si in titlul riscant in punctul de tangenta. Cu certitudine, portofoliile de pe aceasta dreapta sunt preferate portofoliilor de pe curba AB ce sunt alcatuite numai din titluri riscante, intrucat primele ofera castiguri mai mari la un nivel dat al riscului.
Este posibila detinerea de portofolii eficiente pe dreapta RfB si dincolo de punctul de tangenta in cazul in care imprumuturile sunt permise.
Figura 11. Frontiera de eficienta in conditii utilizarii acordarii de imprumuturi
|
|
Daca se presupune ca investitorii se imprumuta pentru a cumpara titluri financiare cu acelasi castig cu cel al titlurilor fara risc, portofoliile eficiente aflate dincolo de punctul de tangenta sunt dispuse pe o extrapolare liniara a dreptei, ceea ce este evidentiat in figura 12.
Orice punct de pe dreapta este posibil de obtinut prin combinarea portofoliului format din titluri riscante din punctul B cu titlul fara risc sau prin echilibrarea portofoliului B prin contractarea de imprumuturi si investirea fondurilor in B. Portofoliile de pe dreapta RfBD sunt preferate portofoliilor dintre A si B, B si C pentru ca maximizeaza castigurile prognozate la un anumit nivel al riscului sau minimizeaza riscul la un nivel dat al castigului prognozat. Frontiera de eficienta este in totalitate liniara. Dreapta RfBD este cunoscuta sub denumirea de dreapta pietei de capital. Aceasta conexeaza castigul prognozat al unui portofoliu eficient cu riscul sau determinat pe baza abaterii standard.
Figura 12. Frontiera de eficienta in conditii utilizarii acordarii si contractarii de imprumuturi
|
|
In diagrama
de mai sus, numai un singur portofoliu format din titluri riscante este optim
si este acelasi pentru toti investitorii. In aceste
circumstante, portofoliul optim este portofoliul de piata
adica titlurile sunt incluse in functie de valoarea lor de
piata. Dreapta pietei de capital poate fi exprimata
matematic in termenii ratei dobanzii (castigul titlului fara
risc) si ai castigului portofoliului de piata. Formula de
calcul este urmatoarea: 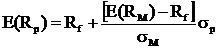
Din formula rezulta ca pentru un portofoliu eficient, castigul prognozat este o functie liniara a riscului sau calculat prin intermediul abaterii standard. Inclinatia dreptei este numita "pretul riscului" (castigul prognozat aditional pentru fiecare unitate aditionala de risc).
In figura 13, rata dobanzii este 4%, castigul prognozat al portofoliului M 10%, abaterea sa standard 12%. Investitorul care opteaza pentru acest portofoliu are un castig de 6% (10%-4%) in conditiile unui risc de 12%. Inclinatia dreptei este de 0,5 (0,06/0,12). Cu alte cuvinte, fiecare unitate suplimentara de risc este recompensata cu o jumatate de unitate suplimentara de castig prognozat.
Figura 13. Dreapta pietei de capital
|
|
Nevoile si preferintele investitorilor individuali vor determina numai valoarea debitelor si a creditelor. Faptul ca alegerea este independenta de combinatia optima a titlurilor riscante este denumita teorema separatiei.
Pentru analiza acesteia vom apela la doua premise. In primul rand, in cazul in care numai acordarea de imprumuturi este permisa, teorema isi pierde valabilitatea. De exemplu, in figura 14, multimea portofoliilor eficiente nu se limiteaza la cele de pe dreapta RfM. Aceasta include si portofoliilor alcatuite din titluri riscante aflate intre M si C ce pot fi preferate de anumiti investitori. Altfel, nu exista o singura combinatie optima de titluri riscante.
In al doilea rand, frontiera de eficienta a portofoliilor formate din titluri riscante poate avea segmente liniare. Daca frontiera este liniara in punctul de tangenta, exista si in acest caz mai multe portofolii optime de titluri riscante, ceea ce este evidentiat in figura 15. Portofoliile B si C, ca si acelea plasate pe dreapta care le uneste, sunt portofolii eficiente de titluri riscante. Desigur, castigurile acestora sunt perfect corelate.
Figura 14. Frontiera de eficienta in absenta contractarii de imprumuturi
|
|
Figura 15. Frontiera de eficienta cu segment liniar
|
|
Markowitz a creat o modalitate de analiza a datelor pentru fiecare valoare mobiliara astfel incat sa poata fi precizate toate portofoliile optime sau eficiente, in sensul ca nici un alt portofoliu nu poate avea ambele atribute superioare. Precizarea unui portofoliu eficient inseamna indicarea ponderilor din resursele investitorului care ar trebui alocate pentru fiecare titlu inclus in portofoliu. Investitorii rationali, care au aversiune fata de risc, vor alege detinerea unuia dintre portofoliile eficiente. In acest subcapitol este abordata problematica alegerii de catre un investitor a acelui portofoliu optim dintre portofoliile eficiente.
Subcapitolele anterioare se bazeaza pe presupunerea ca majoritatea investitorilor prefera castigurile ridicate si totodata au aversiune fata de risc. Definirea portofoliilor eficiente este realizata prin prisma celor afirmate anterior. Date fiind previziunile pentru fiecare titlu financiar si interdependentele dintre acestea, multimea de portofolii eficiente este aceeasi pentru toti investitorii. Tinand cont de faptul ca preferintele investitorilor pentru relatia castig-risc difera, trebuie abordate modalitatile in care un investitor alege un portofoliu optim dintre mai multe portofolii eficiente. Obtinerea valorii maxime implica notiunea de maximizare. Majoritatea investitorilor nu cauta maximizarea castigurilor prognozate. Principiul de baza care ghideaza comportamentul acestora este maximizarea utilitatii prognozate. Utilitatea va fi maximizata atunci cand o anume combinatie de castiguri prognozate si riscuri este preferata in raport cu toate celelalte combinatii.
In continuare, se analizeaza relatiile dintre portofoliile eficiente si functiile de utilitate. Functia de utilitate reflecta relatiile dintre avere si utilitate. Banii, ca si celelalte lucruri, au o utilitate marginala in scadere. Relatia este reflecta in figura 16 (utility - utilitate, wealth - avere). Astfel, utilitatea creste, dar intr-un ritm mai redus, odata cu cresterea bogatiei. Fiecare unitate aditionala (marginala) de bogatie ofera o crestere mai redusa a utilitatii decat precedenta unitate. De aceea, curba are forma concava. Ar fi util daca s-ar putea demonstra ca portofoliile care sunt eficiente in termenii mediei si dispersiei sunt acele portofolii care maximizeaza utilitatea prognozata a investitorului. In acest context, toate elementele managementului portofoliului ce par plauzibile ar fi corelate intre ele.
Figura 16. Utilitatea bogatiei
|
|
Pentru
inceput, pentru investigarea relatiilor dintre teoria utilitatii
si portofoliile eficiente, va trebui adancita analiza relatiilor
dintre bogatie si utilitate. Tot ceea ce s-a evidentiat
este faptul ca acea curba ce desemneaza aceasta
relatie are forma concava, putand fi descrisa cu ajutorul
catorva functii matematice. In acest context, este uzuala folosirea
unei ecuatii simple de gradul doi, dupa urmatoarea formula:
![]() , unde U este utilitatea portofoliului, Rp
castigul prognozat al portofoliului; a, b, c constante (b si c au
valori pozitive ce depind de preferintele investitorului).
, unde U este utilitatea portofoliului, Rp
castigul prognozat al portofoliului; a, b, c constante (b si c au
valori pozitive ce depind de preferintele investitorului).
Daca functia de utilitate este reprezentata de ecuatia anterioara, poate fi demonstrat ca utilitatea prognozata depinde numai de media si dispersia distributiei probabile a castigurilor viitoare. Cu alte cuvinte, pentru investitorii ale caror functii de utilitate sunt patratice, abordarea medie-dispersie in selectia portofoliului este valida. Un portofoliu eficient in termenii mediei si dispersiei va maximiza utilitatea prognozata.
Intrucat investitorii prefera cresterea bogatiei si evitarea riscului sau incertitudinii, este posibila conturarea unor combinatii diferite de castiguri si riscuri prognozate care au aceeasi semnificatie pentru un investitor, ceea ce inseamna ca un investitor isi va asuma un risc mai mare, daca dobandeste o bogatie prognozata mai mare. Combinatiile de castiguri si riscuri prognozate care au aceeasi semnificatie sunt dispuse pe asa-numita curba de indiferenta reprezentata in figura 17.
Desigur, fiecare investitor nu are o singura curba de indiferenta, ci o multime infinita de asemenea curbe. Fiecare curba reprezinta multimea de castiguri prognozate si riscuri care au aceeasi semnificatie. Orice investitor isi va plasa resursele astfel incat sa obtina cea mai mare utilitate prognozata. In figura 17, este evident ca investitorul va prefera curba de indiferenta U3 in raport cu U2, U2 in raport cu U1 s.a.m.d.
Figura 17. Exemplu ipotetic privind relatia dintre preferintele pentru castigurile prognozate si risc
|
|
In acest moment, investitorul individual este pregatit din punct de vedere conceptual pentru selectarea portofoliului optim dintre multimea de portofolii eficiente. Portofoliul optim (acela care maximizeaza utilitatea prognozata) se afla la punctul de tangenta dintre frontiera de eficienta si curba de indiferenta. In figura 18 se observa ca cea mai buna optiune este punctul A plasat pe frontiera de eficienta.
Aceasta conexare a teoriei utilitatii cu cea a portofoliului este grevata de cateva deficiente teoretice. Anumiti cercetatori au remarcat ca o functie de utilitate sau o relatie ce are forma patratica in cele din urma va determina reducerea utilitatii odata cu sporirea bogatiei, ceea ce influenteaza negativ demonstratia de mai sus, avand in vedere ca unul dintre putinele lucruri cunoscute cu certitudine de catre economisti este acela ca oamenii prefera intotdeauna detinerea mai multor bani decat mai putini. Pentru iesirea din aceasta dificultate pot fi conturate doua solutii. Prima solutie consta in ignorarea rezultatelor finale si presupunerea ca gradul de relevanta al bogatiei este acela in care utilitatea continua sa creasca, ceea ce este evidentiat in figura 19.
Figura 18. Portofoliul optim in conditiile acordarii
si contractarii de imprumuturi
|
|
O a doua solutie rezida in presupunerea ca, concavitatea nu implica in mod obligatoriu o relatie patratica si ca si alte ecuatii pot fi reprezentate sub forma concava fara a avea o valoare maxima din care utilitatea sa inceapa sa scada pe masura cresterii bogatiei. Carenta acestor curbe consta in faptul ca eficienta unui portofoliu in termenii mediei si dispersiei nu implica neaparat maximizarea utilitatii prognozate. Markowitz a demonstrat ca numeroase functii de utilitate pot fi aproximate convenabil cu ajutorul functiei de gradul doi.
Figura 19. Utilitatea bogatiei
|
|
O alta
deficienta teoretica este data de cei care sustin
ca selectia portofoliului prin intermediul criteriilor
medie-dispersie nu este adecvata. Anumite portofolii eficiente pot fi
inacceptabile daca cele mai bune castiguri care le sunt asociate sunt
mai reduse decat cele mai mici venituri asociate altor portofolii eficiente. Sǎ
luǎm in considerare douǎ portofolii A si B, ce au
caracteristicile descrise anterior. Cand castigurile sunt distribuite
normal, ![]() pot fi
considerate intervale de incredere. Portofoliul A nu ar trebui ales de nici un
investitor intrucat cel mai mare venit posibil al sau ofera un
castig prognozat mai redus (10%) decat cel mai redus venit posibil al
portofoliului B (11%).
pot fi
considerate intervale de incredere. Portofoliul A nu ar trebui ales de nici un
investitor intrucat cel mai mare venit posibil al sau ofera un
castig prognozat mai redus (10%) decat cel mai redus venit posibil al
portofoliului B (11%).
Alti critici au argumentat ca investitorii pot fi interesati de caracteristicile distributiilor castigurilor prognozate suplimentare mediei si dispersiei. In particular, acestia sustin ca gradul de oblicitate poate avea relevanta. Astfel, daca castigurile prognozate ale portofoliilor au aceeasi medie si dispersie, dar diferite grade de oblicitate, investitorii pot prefera distributia care este inclinata catre dreapta.
Tabelul 3. Veniturile posibile pentru portofoliile A si B
|
A |
B |
|
|
|
8% |
15% |
|
|
4% |
16% |
|
|
2% |
4% |
|
|
10% |
19% |
|
|
l6% |
11% |
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |