Acceleratia
Acceleratia caracterizeaza variatia in timp a vitezei, fiind la randul ei, o marime fizica vectoriala. Acceleratia medie a unui mobil pe traiectoria sa este definita prin relatia:
iar acceleratia momentana (instantanee):
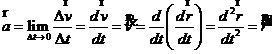 .
.
Acceleratia este un vector care are
orientarea lui ![]() . Aceasta reprezinta derivata de ordinul intai a vitezei
in raport cu timpul, respectiv derivata de ordinul doi a vectorului de
pozitie in raport cu acelasi parametru.
. Aceasta reprezinta derivata de ordinul intai a vitezei
in raport cu timpul, respectiv derivata de ordinul doi a vectorului de
pozitie in raport cu acelasi parametru.
Proiectiile acceleratiei (momentane) intr-un sistem de coordonate carteziene sunt:
deci ![]() ,
,
iar modulul ![]() .
.
Formula dimensionala a
acceleratiei este: 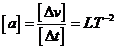 , iar unitatea de masura
, iar unitatea de masura ![]() .
.
In miscarea curbilinie, vectorul viteza isi
modifica in general in timp atat directia cat si modulul. Pentru
o astfel de miscare, variatia ![]() a vitezei intre
doua puncte de pe traiectorie poate fi descompusa intr-o
componenta tangentiala
a vitezei intre
doua puncte de pe traiectorie poate fi descompusa intr-o
componenta tangentiala ![]() (tangenta la
traiectorie) si o componenta normala
(tangenta la
traiectorie) si o componenta normala ![]() (avand directia
razei de curbura) (Fig. 2.5):
(avand directia
razei de curbura) (Fig. 2.5):
|
|
|
Fig. 2.5. Acceleratia liniara in miscarea curbilinie
Acceleratia mobilului poate fi scrisa:
Notand ![]() si
si ![]() , se obtine
, se obtine ![]() , unde
, unde ![]() este acceleratia tangentiala,
iar
este acceleratia tangentiala,
iar ![]() acceleratia normala. Acceleratia
tangentiala corespunde variatiei modulului vitezei si are
directia si sensul vitezei in punctul considerat. Acceleratia
normala corespunde variatiei directiei vitezei si are
directia razei de curbura, fiind perpendiculara pe directia
vitezei in punctul respectiv. Acceleratiei normala este
orientata spre centrul cercului de curbura si din acest motiv
mai este numita acceleratie radiala sau acceleratie
centripeta (Fig. 2.5).
acceleratia normala. Acceleratia
tangentiala corespunde variatiei modulului vitezei si are
directia si sensul vitezei in punctul considerat. Acceleratia
normala corespunde variatiei directiei vitezei si are
directia razei de curbura, fiind perpendiculara pe directia
vitezei in punctul respectiv. Acceleratiei normala este
orientata spre centrul cercului de curbura si din acest motiv
mai este numita acceleratie radiala sau acceleratie
centripeta (Fig. 2.5).
La limita, cand ![]() , respectiv
, respectiv ![]() , se poate scrie:
, se poate scrie: ![]() , de unde:
, de unde:
prin urmare ![]() este
perpendiculara pe planul definit de
este
perpendiculara pe planul definit de ![]() si
si ![]() . Vectorii
. Vectorii ![]() si
si ![]() fiind perpendiculari,
fiind perpendiculari, ![]() , deci modulul acceleratiei normale este:
, deci modulul acceleratiei normale este:
Acceleratia unghiulara in miscarea curbilinie reprezinta variatia in timp a vitezei unghiulare. Acceleratia unghiulara medie este:
iar acceleratia unghiulara momentana (instantanee):
Dimensiunea si unitatea de masura a acceleratiei unghiulare sunt:
![]() , respectiv
, respectiv ![]() .
.
Vectorul acceleratie
unghiulara are directia vitezei unghiulare ![]() , iar sensul coincide cu sensul lui
, iar sensul coincide cu sensul lui ![]() daca
miscarea este accelerata, respectiv este contrar lui
daca
miscarea este accelerata, respectiv este contrar lui ![]() daca
miscarea este incetinita. Modul acceleratiei unghiulare poate fi
scris:
daca
miscarea este incetinita. Modul acceleratiei unghiulare poate fi
scris:
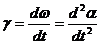
Relatia dintre acceleratia tangentiala si acceleratia unghiulara, pe baza formulelor (2.13) si (2.23) este data de:
|
|
|
Fig. 2.6. Acceleratia unghiulara, acceleratia tangentiala si acceleratia normala
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |