Dinamica punctului material
Dinamica este acea parte a mecanicii care studiaza miscarea corpurilor tinand cont de interactiunile acestora cu exteriorul, adica tinand cont de fortele care actioneaza asupra acestora.
La baza dinamicii miscarii corpurilor stau trei principii, enuntate de catre Newton, care au urmatoarele exprimari :
Principiul
I al dinamicii sau principiul inertiei : Un corp se misca rectiliniu si
uniform, sau se afla in repaus relativ, atata timp cat asupra lui nu actioneaza
forte din exterior Principiul II al dinamicii sau principiul
fortei : Daca asupra unui corp cu masa m actioneaza o forta ![]() aceasta imprima
corpului o acceleratie direct proportionala cu forta
aceasta imprima
corpului o acceleratie direct proportionala cu forta ![]() si invers
proportionala cu masa corpului
si invers
proportionala cu masa corpului
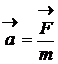 (1.16)
(1.16)
Pricipiul III al dinamicii sau principiul egalitatii actiunii si reactiunii: Daca un corp actioneaza asupra altui corp cu o forta numita actiune, cel de-al doilea corp actioneaza cu o forta egala si de semn contrar, numita reactiune, asupra primului. Actiunea si reactiunea sunt intodeauna egale in modul si actioneaza asupra unor corpuri diferite.
Ecuatia (1.16) reprezinta legea fundamentala a dinamicii si daca tinem cont ca:
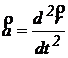 (1.16')
(1.16')
atunci se poate vedea ca (1.16) devine o ecuatie diferentiala a carei solutie ne permite gasirea legilor de variatie a vitezei respectiv a coordonatelor in raport cu timpul si anume:
![]() 1.17)
1.17)
![]() (1.18)
(1.18)
Constantele de integrare C1..6 se determina din conditiile initiale, care inseamna cunoasterea pozitiei si vitezei la momentul t0.
![]() (1.19)
(1.19)
![]() (1.20)
(1.20)
Din legea fundamentala a mecanicii rezulta trei teoreme:
a) Teorema impulsului
Definim marimea fizica vectoriala numita impuls (sau cantitatea de miscare), egala cu produsul dintre masa corpului si viteza acestuia.
![]() (1.21)
(1.21)
Matematic mai putem scrie
![]() (1.22)
(1.22)
si deci
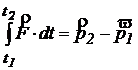 (1.23)
(1.23)
Marimea
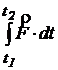 (1.24)
(1.24)
se numeste impulsul fortei rezultante aplicate punctului material si este egala cu variatia impulsului punctului material.
Enuntul de mai sus constituie teorema impulsului si se poate observa din (1.23) ca un punct material nu-si poate schimba de la sine impulsul sau, numai daca asupra lui actioneaza o forta.
b) Teorema momentului cinetic
Consideram un corp rigid de data aceasta, care se
poate roti in jurul unei axe, sub actiunea fortei ![]()
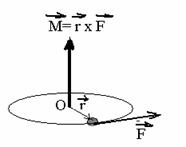
Fig. 1.7 Momentul fortei
Efectul
de rotatie al corpului este determinat de forta ![]() si de distanta suportului sau pana la
polul O, aflat pe axa de rotatie. Definim atunci marimea :
si de distanta suportului sau pana la
polul O, aflat pe axa de rotatie. Definim atunci marimea :
![]() (1.25)
(1.25)
numita momentul fortei fata de punctul O.
Definim de asemenea marimea
![]() (1.26)
(1.26)
numita moment cinetic (vezi figura 1.8)
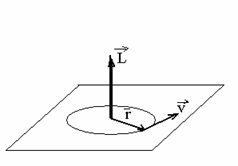
Fig. 1.8 Momentul cinetic
Prin derivare obtinem :
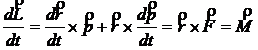 (1.27)
(1.27)
adica
![]() (1.28)
(1.28)
de unde
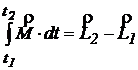 (1.29)
(1.29)
Relatia (1.29) ne arata ca momentul fortei aplicate unui punct material este egal cu variatia momentului cinetic al punctului material. Enuntul de mai sus constituie teorema momentului cinetic.
c) Teorema energiei cinetice
Fortele pot produce deplasari ale corpurilor pe o directie, in functie de orientarea acestora. O masura a efectului actiunii unei forte, este exprimata de catre lucrul mecanic. Prin definitie lucrul mecanic elementar este dat de:
![]() (1.30)
(1.30)
Daca forta ![]() este constanta atunci:
este constanta atunci:
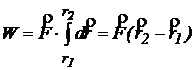 (1.31)
(1.31)
Daca forta nu este onstanta atunci integrarea depinde de expresia de dependenta a fortei. Din (1.30) se mai obtine:
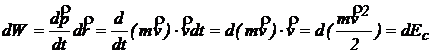 (1.32)
(1.32)
unde
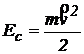 reprezinta
energia cinetica a corpului supus actiunii fortei
reprezinta
energia cinetica a corpului supus actiunii fortei ![]() . Prin integrare rezulta
. Prin integrare rezulta
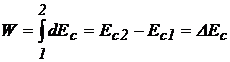 (1.33)
(1.33)
adica:
Lucrul mecanic efectuat de o forta rezultanta aplicata punctului material, este egal cu variatia energiei cinetice a punctului material
Este evident ca, daca rezultanta fortelor aplicate este permanent nula, energia cinetica a punctului material se conserva.
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |